基于GeoGebra 的一类四点共圆问题的探究与推广

江苏省常州市第二中学(213003) 王 强 黄 雯

解析几何是用代数方法研究几何问题的数学分支,既是近现代数学的重要内容,又是高中数学课程的主干内容. 平面解析几何的研究方法是通过建立几何图形的代数方程(或不等式),实施代数运算,并由代数运算的结果得到几何图形的性质.

四点共圆是一类富有和谐美的几何问题,如何将其转化成为代数问题是一个难点, 在全国高考和各地模考中四点共圆问题经常出现. 文[1]通过对五道高考试题中的四点共圆进行赏析, 统一使用了圆的定义进行证明. 文[2]通过对文[1]中的四点共圆的结论进行推广,统一使用了相交弦定理的逆定理进行证明. 本文利用解析法,借助两个结论:共底边的两个三角形顶角相等,且在底边的同侧,则四点共圆;凸四边形对角互补, 则四个顶点共圆, 对数学通报上一类四点共圆问题进行了解法探究并进行了类比推广,借助GeoGebra 软件先猜再证,得到了一些美妙的结论,将其整理下来与读者共享. 探究中笔者深切感受到GeoGebra 软件在圆锥曲线问题研究中的绘图简便性,更感受到圆锥曲线的内在统一性.

1. 探究由来,问题呈现

《数学通报》2021 年11月数学问题2629: 设双曲线C的两焦点为F1,F2,两准线为l1,l2, 过双曲线上一点P,作平行于F1F2的直线, 分别交准线l1,l2于M1、M2,直线M1F1与M2F2交于点Q,则:P,Q,F2,F1四点共圆,如图1所示.

图1

《数学通报》上的解答是用共底边的两个三角形顶角相等,且在底边的同侧,则四个顶点共圆的方法证明的,笔者读后深有启发. 同时,也产生了一些疑惑,(1)过点P不作平行于F1F2的直线,其他过点P的直线有这样的性质吗? (2)将双曲线改成椭圆,结论还成立吗? 笔者借助GeoGebra 软件,先通过作图进行直观观察,然后再进行严格证明,探究出了一些美妙的结论,从而解决了疑惑.

2. 类比推广,横纵拓展

定理1 设双曲线C的两焦点为F1,F2,两准线为l1,l2,过双曲线上一点P处的切线为l,l分别交准线l1、l2于M1、M2, 直线M1F1与M2F2交于点Q, 则P,Q,F2,F1四点共圆, 如图2 所示.

图2

因 为tan ∠F1PF2= tan ∠F1QF2, 所 以∠F1PF2=∠F1QF2,故P,Q,F2,F1四点共圆.

定理2 设椭圆C的两焦点为F1,F2,两准线为l1,l2,过椭圆上一点P,作平行于F1F2的直线,分别交准线l1、l2于M1、M2, 直线M1F1与M2F2交于点Q, 则P,Q,F2,F1四点共圆,如图3 所示.

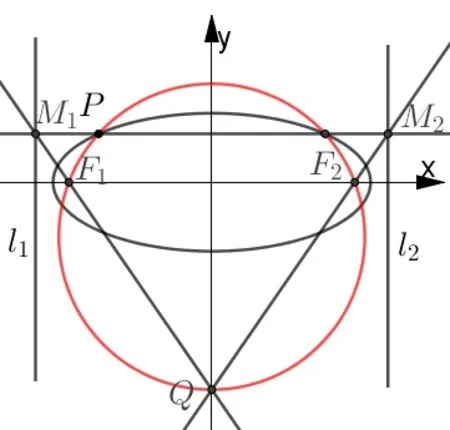
图3

定理3 设椭圆C的两焦点为F1,F2,两准线为l1,l2,过椭圆上一点P处的切线为l,l分别交准线l1、l2于M1、M2,直线M1F1与M2F2交于点Q,则P,Q,F2,F1四点共圆,如图4 所示.

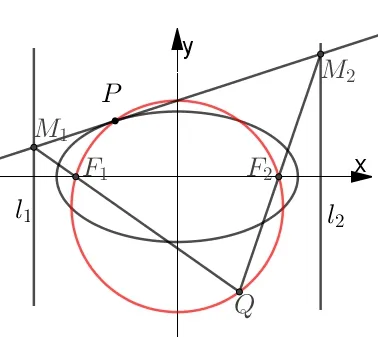
图4

定理3 的证明和定理1 的证明相似,这里不再赘述.

3. 再用技术,引申结论

因为抛物线只有唯一的焦点和准线,上面的定理无法直接类比推广, 那么抛物线中是否有类似的四点共圆的结论呢? 笔者再次利用GeoGebra 进行先绘图感知,后推理论证,得到了定理4-6.

定理4 设抛物线C的焦点为F,准线为l,过抛物线上一点P,作平行于抛物线对称轴的直线交准线l于M1,作点P处的切线交准线l于M2,则P,F,M2,M1四点共圆,如图5 所示.

图5

定理5 设椭圆C上一点P, 作平行于椭圆长轴的直线交准线l于N, 作点P处的切线交同一准线l于M, 则P,N,M和准线l相对应的焦点F四点共圆,如图6 所示.

图6

定理6 设双曲线C上一点P,作平行于双曲线实轴的直线交准线l于N,作点P处的切线交同一准线l于M,则P,N,M和准线l相对应的焦点F四点共圆,如图7 所示.

图7

定理5-6 的证明和定理4 的证明相似,这里不再赘述.

4. 探究反思,技术助力

著名数学教育家波利亚说过:“没有一道题是可以解决得十全十美的,总剩下些工作要做,蘑菇总是成堆生长的,经过充分的探讨与钻研,总会有点滴的发现,总能改进这个解答,而且在任何情况下,我们都能提高自己对这个解答的理解水平. ”类比、联系、推广是数学研究中的常用方法,只要我们善于类比和勇于探究,会发现圆锥曲线中有很多相似的结论,而GeoGebra 的应用能协助我们发现结论. 在几何图形展示的过程中,我们不仅能感受到数学的对称美,更能提高我们发现问题和提出问题的能力.

章建跃教授提出“四个理解”是落实核心素养的关键,“理解技术”就是要懂得如何有效利用技术帮助学生的学和教师的教. 本探究中充分发挥GeoGebra 在绘制圆锥曲线图形中的简便性,通过作图观察提出猜想,利用解析法证明猜想. 从探究中我们可以感受到GeoGebra 软件不仅是一个几何图形动态展示的强大工具,更是一个数学探究学习的有效利器.