用程序设计实现四阶全对称幻方的构造

许芝卉，李建华

（山西大同大学数学与统计学院，山西大同 037009）

定义1设A=(aij)n×n(1≤i,j≤n)，含数集N={1,2,3,…,n2}的全部元素，若A中的诸元素是按自然数从小到大的顺序排列而成，则称方阵A为自然方阵[1]。

定义2设方阵含数集N={1,2,3,…,16}的全部元素，若该方阵每行、每列及主、副对角线元素之和都相等，都等于幻和值34，则称该方阵为四阶全对称幻方[2]。

定义3设有四阶方阵，将字母a,b,c,d和数字0,1,2,3这八个元素对应起来，使a,b,c,d四个字母在每一行、每一列及主、副对角线上只出现一次，且每个数字和每个字母不会相遇两次。此时的幻和值是a+b+c+d+6=34。称这种幻方为字母和数字组合幻方，简称组合幻方[1]。

定理1自然方阵A=(aij)n×n(1≤i,j≤n)，(其中n=4)经过以下几种方法构造而成的方阵，若满足幻和值都相等，则该方阵为四阶全对称幻方[2]。

四阶幻方是最简单的双偶幻方，关于四阶幻方的构造方法介绍如下3种情况。

1 自然方阵对称交换构造法

（1）顺序填数（自然方阵，如图1）。

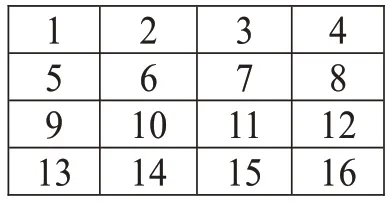
图1 自然方阵

（2）以中心点对称互换数字。

（I）以中心点对称交换对角线上的数，即1－16，6—11，4－13，7－10 互换位置（如图2），其幻和值为34。

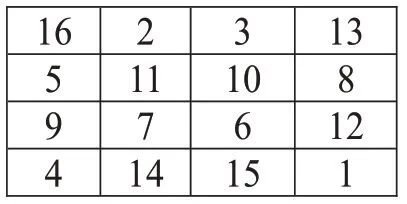
图2 对称幻方1

（Ⅱ）以中心点对称交换非对角线上的数，即2－15，3－14，5－12，8－9（如图3）。

（Ⅲ）由图3 中互换二、三行元素，即12－8，6—10，7－11，9－5（如图4）。

（Ⅳ）由图3 中互换二、三列元素，即15－14，6—7，10－11，3－2（如图5）。图5 中互换二、三行元素，可得图6。当然由图4、图5、图6 仍能构造出不同的幻方[3]。

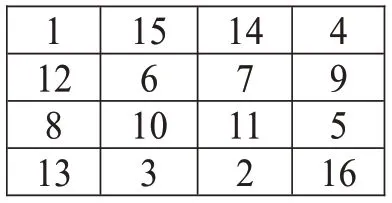
图3 对称幻方2

图4 对称幻方3

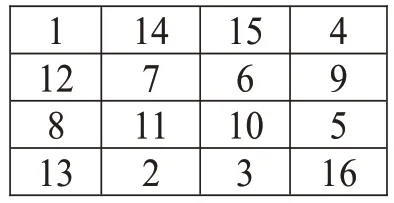
图5 对称幻方4

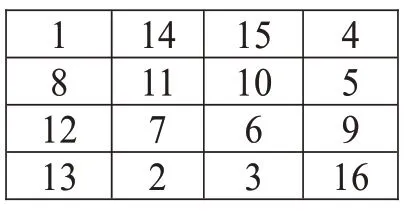
图6 对称幻方5

2 字母数学组合构造法

对定义3 中的字母和数字组合幻方，若再给定{a,b,c,d}={1,5,9,13}。这里采用集合的写法，而集合又具有无序性和不重复性。因此上面集合共有24种不同的全排列。当然可构造24 种全对称四阶幻方。具体方法如下：

（1）将a,b,c,d和数字0,1,2,3 组合填入方阵（如图7）。

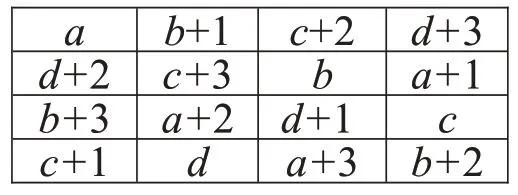
图7 字母数字组合方阵

（2）a,b,c,d可以任意排列，可得到24 种不同的四阶全对称幻方。

（3）构造全对称幻方程序文件为file1.cpp，且程序能够正确运行，并能得到满意的结果（如图8）。

按上面方法构造的四阶幻方程序如下[4]，程序文件名为file1.cpp。

程序运行的部分结果如图8。

图8 file1.cpp文件运行结果

3 程序设计构造法

定义一个数组，让数组元素按自然方阵排列，对换方阵中元素的位置，经过对换后的方阵，应满足：①每个位置上的元素必须互不相同；②每行、每列、及主、副对角线上元素之和都相等，都等于幻和值34。

通过编写程序来实现上面的操作，同时在程序中加以验证。若满足条件，就输出该幻方，若不满足，则通过循环继续进行上述操作。这样构造的幻方共有880 个，设计的程序，只构造四阶幻方中第一个元素为1 的情况，这样的幻方共有416 个。且程序能够正确运行，并可得到满意的结果（如图9）。按上述方法生成四阶幻方的程序如下[4]，

程序文件名为file2.cpp。

程序运行的部分结果如图9。

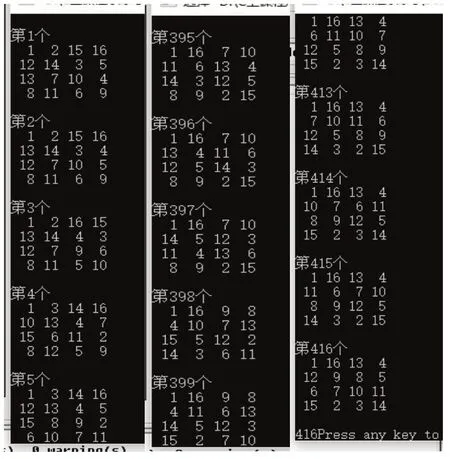
图9 file2.cpp文件运行结果

4 结语

幻方的构造多种多样，形态变化万千，它所蕴含的哲学思想最为丰富，给人以美的遐想，论文中的四阶全对称幻方就具有富态的美。当然幻方的研究是无止境的，将会探讨四阶幻方是否存在平方幻方，仍用程序设计来实现并加以验证。（注：若四阶全对称幻方同时满足每行、每列及主、副对角线上元素的平方和也都相等，则该幻方为四阶全对称平方幻方。）