基于机器学习的碳酸盐微观结构与性质

杨 博， 路贵民

（华东理工大学国家盐湖资源综合利用工程技术研究中心，上海 200237）

熔盐作为一种传蓄热介质，广泛应用于聚焦式光热发电(Concentrating Solar Power, CSP)中[1-2]。在美国国家能源局提出的第3 代光热发电技术的路线图中，将采用超临界二氧化碳-布雷顿循环系统代替现有的蒸汽-朗肯循环系统进行发电[3]。这项新的技术要求传蓄热介质的工作温度为520～720 ℃，热稳定性优异且腐蚀性相对较小的碳酸盐[3-4]可以满足这一要求。研究碳酸盐的微观结构以及微观性质可以帮助提高基于碳酸盐的传蓄热介质的性能，但是，开展高温熔盐结构信息的实验研究比较困难，高温实验也容易造成数据波动和误差。

随着计算机技术的进步，计算机模拟发展成为一项成熟的分子模拟技术。基于密度泛函理论(Density Functional Theory, DFT)的量子力学计算以及经典分子动力学(Classical Molecular Dynamics,CMD)模拟广泛应用于熔盐的分子模拟领域[5-12]。Koishi 等[13]在Li2CO3-K2CO3的CMD 模拟计算中采用了基于Tosi-Fumi 公式的势函数进行运算，但是他将视作1 个以C 为中心，3 个O 呈等边三角形分布的固定分子，忽略了的分子内作用。Costa[14]在Li2CO3-K2CO3的CMD 模拟中采用FC 极化模型(Fluctuating Charge Model)，将的分子内作用引入模拟体系中。Du 等[15]利用包含库仑项的BornMayer势函数模拟了Na2CO3的结构与性质，计算结果表明模拟计算的为一个金字塔型的立体结构。Desmaele 等[16]采用CMD方法计算碳酸盐的结构与性质，用3 个经验公式分别描述的C-O 相互作用、O-O 相互作用以及与阳离子的相互作用，经验公式的计算参数由基于DFT 的AIMD(ab initio Molecular Dynamics)计算优化，计算结果表明熔融状态下碳酸盐的阴阳离子之间处于相互牵扯的状态，阳离子包裹阴离子并且将其引入第2 配位层，同时阴离子的1～2 个O 原子包裹着阳离子；还发现包裹阳离子的O 原子数量不受阳离子种类和大小的影响。Kiyobayashi等[17]计算了A2CO3(A 为Li、Na、K、 Rb、Cs)的离子电导率，用Born-Mayer-Huggins势函数描述离子之间作用，并用3 个经验公式描述的键角。Roest 等[18]在对碳酸熔盐燃料电池的带电界面进行CMD 模拟时同样采用Born-Mayer-Huggins 势函数描述离子之间作用。

势函数和经验参数是CMD 模拟的基础，势函数及经验参数的选择是否合理直接影响计算结果的准确度，通常势函数以及参数通过实验结果或者量子力学计算进行优化。本文采用基于DFT 理论的第一性原理计算(First-principle Molecular Dynamics, FPMD)、机器学习(Machine Learning, ML)和CMD 方法，建立深度势分子动力学模拟方法(Deep Potential Molecular Dynamics, DPMD)。在DPMD 方法中，ML 将DFT 的结果拟合为CMD 可以识别的深度势(Deep Potential,DP)，而不是通过DFT 优化CMD的势函数。本文对K2CO3和Na2CO3进行DPMD 模拟，计算K2CO3和Na2CO3的结构信息及其部分物理性质，探究DPMD是否可以应用于碳酸盐体系。

1 计算方法

1.1 第一性原理计算

采用 VASP.5.4.4(Vienna ab-initio Simulation Package)软件包进行第一性原理计算。PBE (Perdew-Burke-Ernzerhof)函数用于交换和关联计算[19]，PAW(Projector-Augmented Wave)用于描述原子核和价电子的相互作用[20-21]。氧的价电子构型选择为2s22p4，碳的价电子构型选择为2s22p2，钾的价电子构型选择为3s23p64s1。根据VASP 参数手册的推荐，截断能设置为560 eV，参数K 点设置为1×1×1，模拟过程中的温度控制采用Nose-Hoover 恒温器方法。

第一性原理的计算分为3 步。在温度2 000 K 下运行6 000 个时间步(6 ps)快速获取模型的合理构型，然后以179 K/ps 的冷却速率降温至目标温度1 180、1 230、1 280 K，最后在目标温度下运行20 000 个时间步(20 ps)。

1.2 拟合深度势 (DP Train)

DeepMD-kit.1.2 软件包用于构建深度势函数模型[22-23]。系统的能量定义为每个原子能量的加和，如式(1)所示：

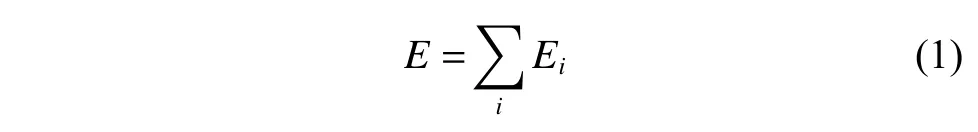
其中：Ei是以原子i为球心，截断半径(rc)为半径的球形空间的能量，Ei定义如式(2)所示：

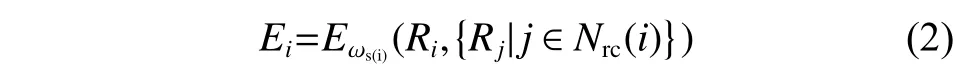
其中：Ri={xi,yi,zi} ，表示原子i的坐标；Rj={xj,yj,zj} ，表示原子j的坐标；Nrc(i)是模拟过程中原子i的临近列表；s(i)表示原子i的化学类别。Ei对Ri的依赖关系通过深度神经网络(Deep Neural Network, DNN)参数化，DNN 的参数ω由机器学习过程控制，采用Adam method 方法优化[24]。

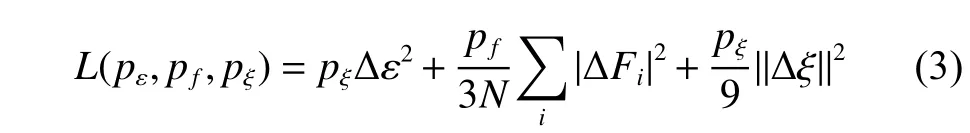
其中：L表示损失函数；pε、pf、pξ是可调节因子；N是原子的总数目； Δ ε 代表机器学习预测数据与对应的第一性计算结果的能量的差值； ΔFi代表机器学习预测数据与对应的第一性计算结果的受力的差值； Δ ξ 是预测数据与第一性计算结果张量除以N的差值。

DeepMD-kit.1.2 中，Zhang 等[25]提出一个灵活的描述符，通过将坐标转化为矢量的方法来保持体系的对称性，解决了模拟体系的原子坐标无法直接应用于机器学习过程的问题，许多计算工作验证了其可靠性[23,26-27]。根据式(4)，体系的原子坐标转变为包含径向信息和角度信息的广义坐标:

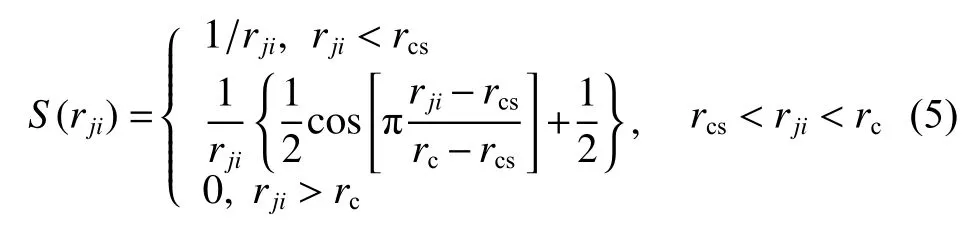
其中：rji为原子j与原子i之间的距离；rcs表示截断半径的平滑参数。

使用DNN 将径向信息映射到矩阵gi1和gi2上，最终，根据式(6)，广义坐标重新编码为特征矩阵Di。

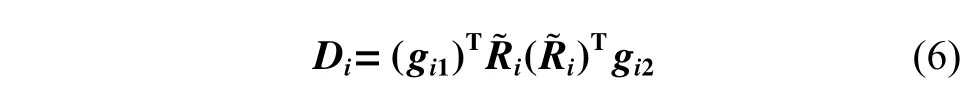
第一性原理的计算结果使用python 代码处理，作为机器学习的输入数据集。机器学习的过程中，第一性原理计算的前15 000 个时间步(15 ps)的结果用于拟合深度势，后5 000 个时间步(5 ps)的计算结果用于测试深度势的精度。嵌入神经网络设置3 个隐藏层，隐藏层大小分别为25、50、100，拟合神经网络大小设置为240、240、240，深度学习过程共持续1 000 000 步。

1.3 经典分子动力学模拟

CMD 的计算使用Lammps(Large-scale Atomic/Molecular Massively Parallel Simulator)软件包完成，采用1.2 节中的深度势代替势函数公式进行运算。计算中采用周期性边界条件(Periodic-Boundary-Condition，PBC)消除表面效应，保证体系粒子数目恒定，采用Verlet 算法求解牛顿方程，设置时间步长=1 ps[28]。

学生虽然深知“数学解题就是由未知向已知不断转化的过程”，但考试时却又常常受制于“转化目标不明”和“调控受阻思维能力不强”两大因素，导致无谓失分．因此，从教“怎样想”入手，深入挖掘中考试题解题思路的生成过程，培养学生良好的思维习惯，对提升转化能力必大有裨益．

Lammps 模拟计算中，计算开始时原子会获得一个遵循高斯分布的随机初速度，性质计算均在等温等压系综(NPT)或者正则系综(NVT)下进行，温度控制使用Nose-Hoover 恒温器方法和Barostat 方法[29-30]。

径向分布函数gαβ(r) 和配位数Nαβ是表征熔盐微观结构的常用方法，其计算公式如式(7)和式(8)所示：

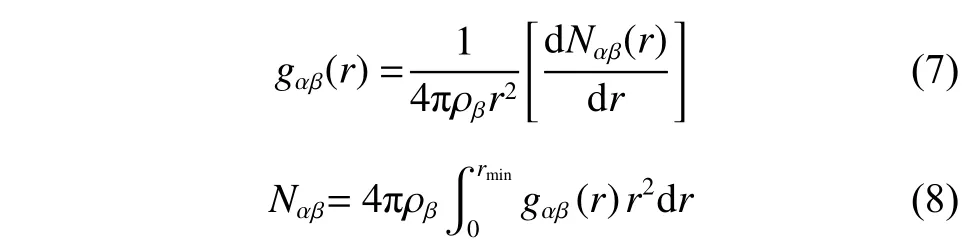
其中： ρβ是β原子的数密度；r表示两个原子之间的距离；Nαβ(r) 是式(1)中提到的微小空间内β原子的平均数目；rmin是径向分布函数(RDF)第一峰峰谷的位置。

密度计算根据式（9）在NPT 系综下进行：

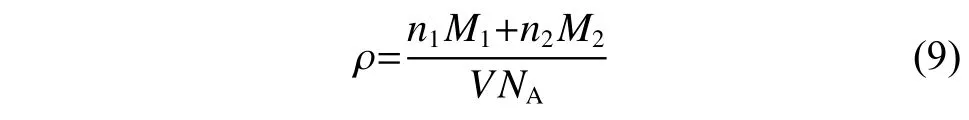
其中：n是原子的数目；M是摩尔质量；V是体系平衡体积；NA是阿伏伽德罗常数。

比热容(Cp)用于描述熔盐吸放热能力的强弱，在模拟计算密度时，可以通过统计体系的焓值随温度的变化情况来计算，计算公式如式(10)所示：

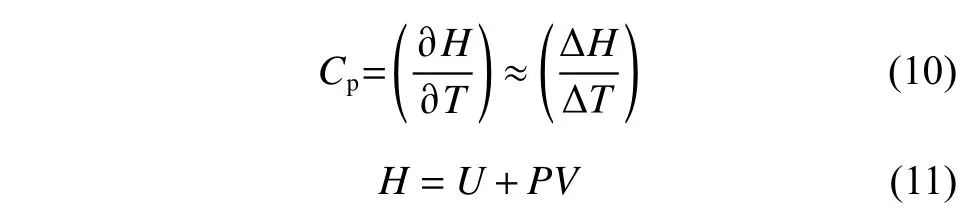
其中：H为体系的焓值；P为压力；U为系统内能，包括动能与势能。

热导率采用逆非平衡分子动力学方法(Reverse Nonequilibrium Molecular Dynamics Method,rNEMD)[31-32]计算。将体系沿z轴方向扩展1 倍然后等分为n层，将第1 层动能最大的原子与(n/2+1)层动能最小的原子每隔一段时间进行动能交换，等待体系达到动态平衡后统计体系中动能交换的大小以及监测体系的温度梯度，可通过式(12)计算热导率：

黏度 ( η) 采 用EMD 方法(Equilibrium Molecular Dynamics Method)进行计算，EMD 方法基于Green-Kubo 公式，通过计算应力张量自相关系数(Stress Tensor Auto-correlation Functions，SACF)得到体系的黏度。Green-Kubo 公式如下：

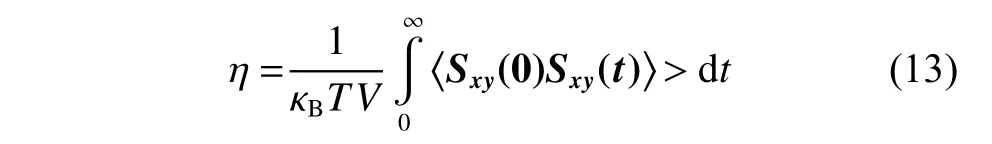
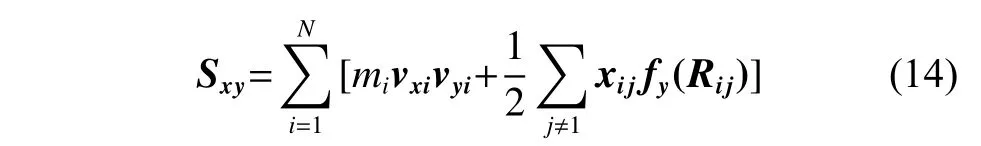
其中：mi为原子i的质量；vxi和vyi分别为原子i在x和y方向的速度分量；fy(Rij)是原子j对原子i在y方向的作用力；Rij表示原子i、j的适量距离；xij是Rij在x方向的分量。

2 结果与讨论

2.1 机器学习的误差

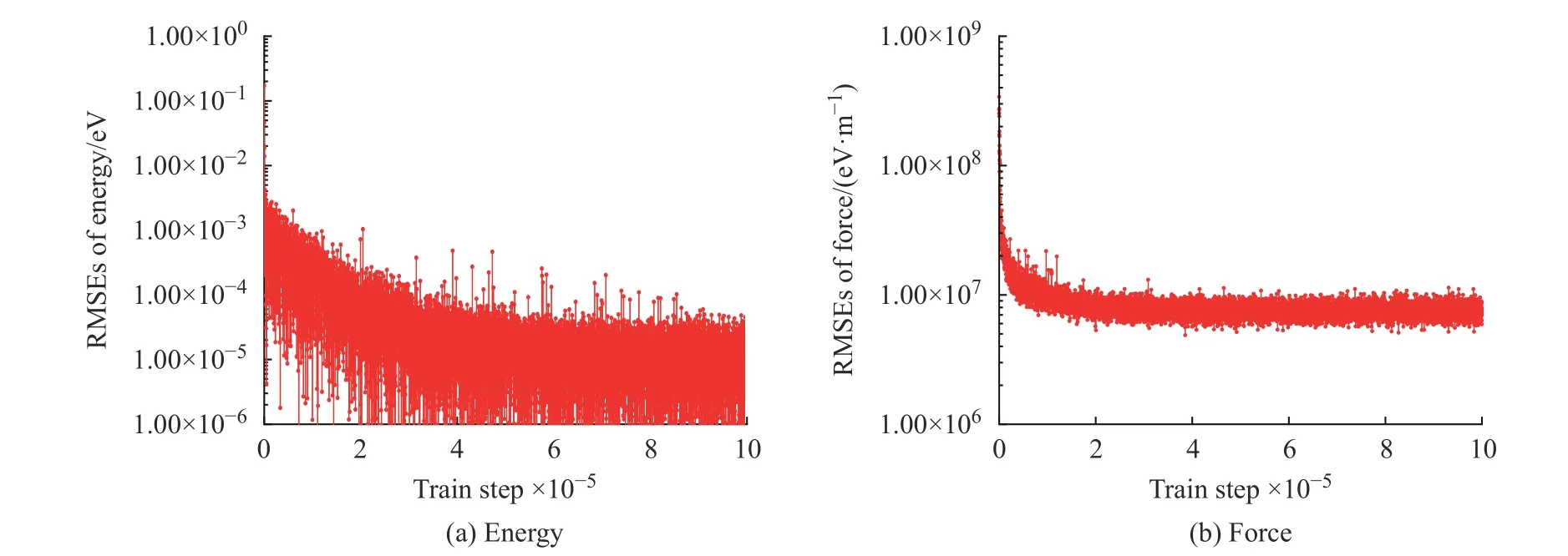
图1 学习过程中K2CO3 能量和受力的均方根误差Fig. 1 EMSEs of energy and force of K2CO3 during learning process

学习过程中K2CO3能量和受力的均方根误差(Root Mean Square Error, RMSEs)如图1 所示，图中数据说明6×105～10×105个步长的训练满足拟合势函数模型的要求，随着学习时间的增加，能量的均方根误差在1.00×10-4eV 以下，受力的均方根误差在1.00×107eV/m 附近。模型的准确率通过执行拟合验证数据与拟合数据的对比测试进行评估，K2CO3机器学习的预测结果与相对应的DFT 计算结果的对比如图2所示，预测结果与DFT计算值吻合度较好。DeepMDkit.1.2 软件包执行对比测试后显示K2CO3能量和受力的均方根误差非常低，分别为8.62×10-4eV 和4.67×108eV/m，表示势函数模型的精度与DFT 精度接近。图3 示出了学习过程中Na2CO3能量与受力的均方根误差。图4 示出了Na2CO3机器学习的预测结果与DFT 计算值的对比。由图可知，随着学习时间的增加，Na2CO3能量的均方根误差在1.00×10-4eV 以下，受力的均方根误差在1.00×109eV/m 以下，执行对比测试后能量与受力的均方根误差分别为1.19×10-3eV 和5.31×108eV/m。

2.2 结构分析

图5 示出了不同温度下采用DPMD 和DFT方法计算所得的K2CO3径向分布函数曲线的对比，二者的计算结果吻合度较好，表明DPMD 方法可以准确描述K2CO3熔融状态下离子之间的相互作用。

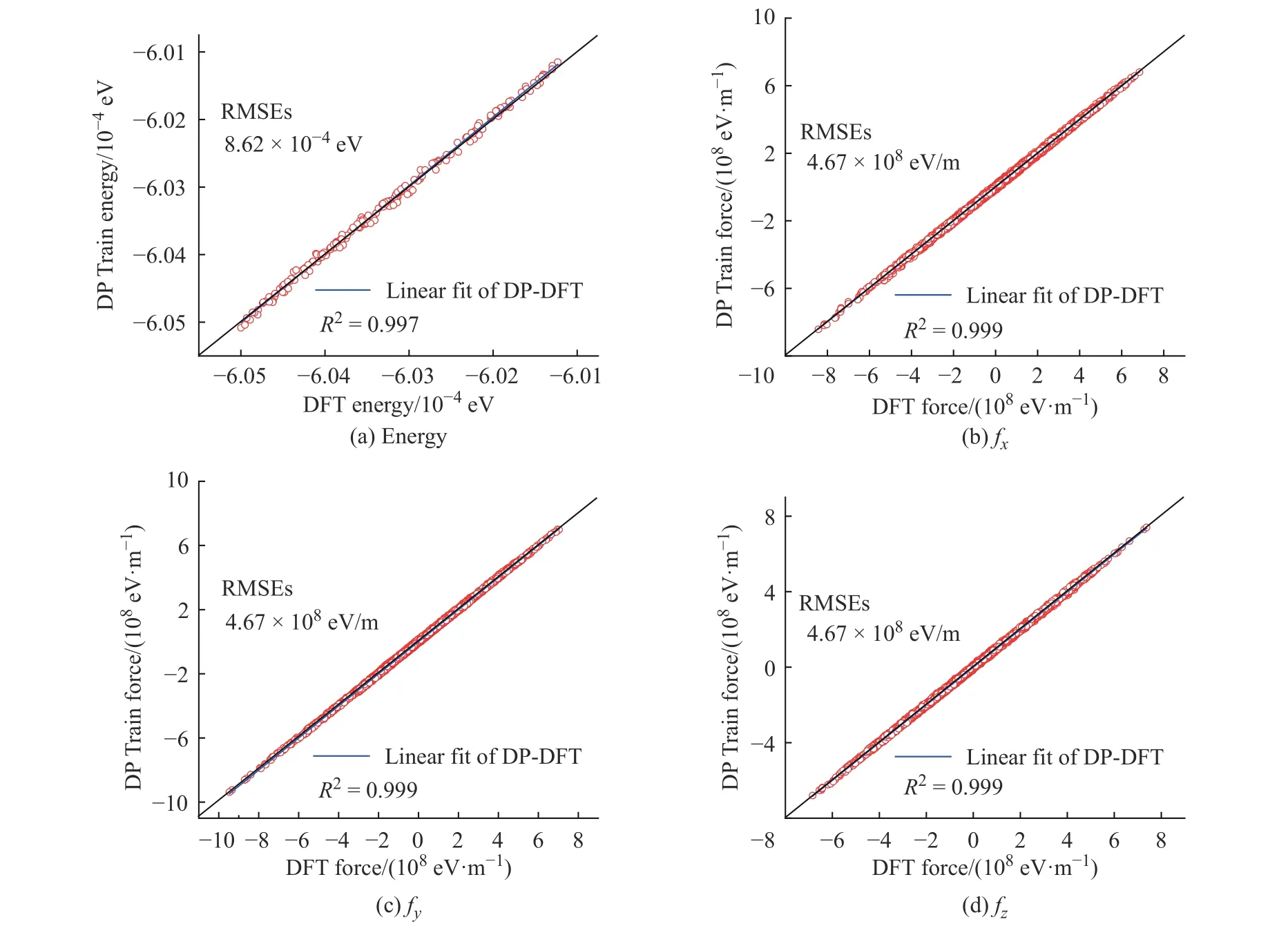
图2 K2CO3 机器学习的预测结果与DFT 计算结果的对比Fig. 2 Comparsion of ML prediction result and DFT calculation result of K2CO3

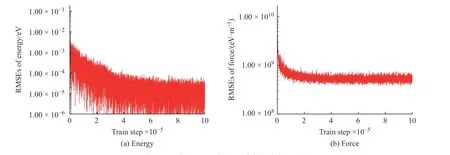
图3 学习过程中Na2CO3 能量和受力的均方根误差Fig. 3 RMSEs of energy and force of Na2CO3 during learning process

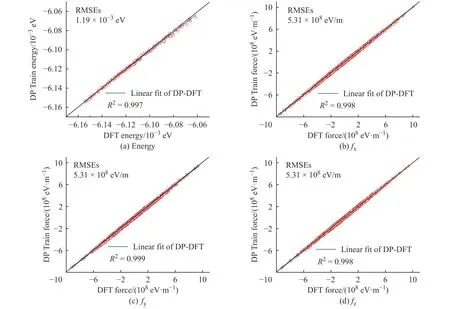
图4 Na2CO3 机器学习的预测结果与DFT 计算结果的对比Fig. 4 Comparsion of ML prediction result and DFT calculation result of Na2CO3

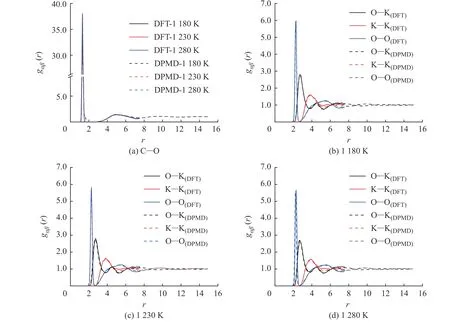
图5 不同温度下K2CO3 径向分布函数的DPMD 与DFT 计算结果对比Fig. 5 Comparsion of radial distribution functions of K2CO3 derived from DPMD and DFT calculation at different temperatures

图6 示出了不同温度下采用DPMD 方法计算的K2CO3部分离子对的径向分布函数曲线。在熔融状态下，所有离子对的径向分布函数曲线都具有相同的特点：每一条曲线都具有非常高的第一峰，在第一峰后的第二峰高度迅速降低，随着距离的增大，径向分布函数曲线逐渐趋近于1.0，这与离子液体“近程有序、长程无序”的特点相对应。第一峰的峰形可以解读出离子对作用的强弱，高而尖的峰代表着排列紧凑有序，矮而宽的峰则代表松散无序。图6(a)中第一峰的峰高随着温度升高而降低，表明随着温度的增加C-O 的相互作用减弱，说明随着温度的升高而略有松散。O-K、K-K 和O-O 的径向分布函数曲线分别如图6(b)、6(c)、6(d)所示，相比于C-O 曲线，O-K、K-K 和O-O 曲线第一峰的峰高随温度升高有一定程度的降低，O-K 第一峰的峰位置随着温度升高略微向右边移动，表明K+与的作用距离在增大。各个离子对的第二峰峰值减弱，峰形变宽，O-O 对的第二峰呈现平台状，而第三峰基本观察不到，说明粒子的不规则性增大，因此可以判断形成了团簇。

图7 示出了采用DPMD 和DFT 方法计算所得的Na2CO3径向分布函数曲线的对比，二者的计算结果吻合度较好。图8 示出了DPMD 方法计算所得的Na2CO3部分离子对的径向分布函数曲线，所有离子对均保持“近程有序、长程无序”的特点，C-O、O-Na、Na-Na 和O-O 离子对曲线的第一峰的峰高均随着温度的升高而降低，说明离子对之间的相互作用在逐渐减弱。图8(a)中C-O 离子对在各个温度点下的径向分布函数曲线的分布趋势高度相似，表明随着温度升高结构保持稳定。O-Na、Na-Na 和O-O 离子对的径向分布函数曲线分别如图8(b)、8(c)、8(d)所示，在1 230 K 和1 260 K 下，3 个离子对的径向分布函数曲线第一峰后的曲线归一化趋势更加明显，表明温度升高以后Na2CO3体系中阴阳离子的不规则性增大。

2.3 性质分析

2.3.1 密度 密度是碳酸盐工业应用的基础性质之一，根据式(9)模拟计算了K2CO3和Na2CO3的密度，计算结果如图9 所示。K2CO3模拟值比文献结果[33]高约5.0%，Na2CO3模拟值比文献结果[33]高约5.6%。随着温度升高，逐渐变得松散以及K、Na 和O 的距离变大，导致K2CO3和Na2CO3的摩尔体积增大，因此密度与温度呈负相关。根据计算值拟合出K2CO3和Na2CO3的密度计算公式分别如式(15)、式(16)所示。

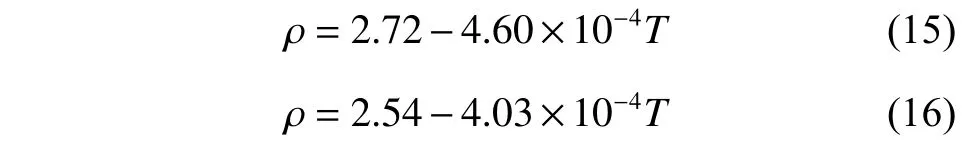
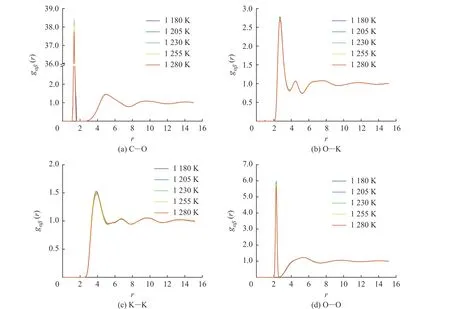
图6 DPMD 方法计算所得的K2CO3 径向分布函数Fig. 6 Radial distribution functions of K2CO3 calculated by DPMD method

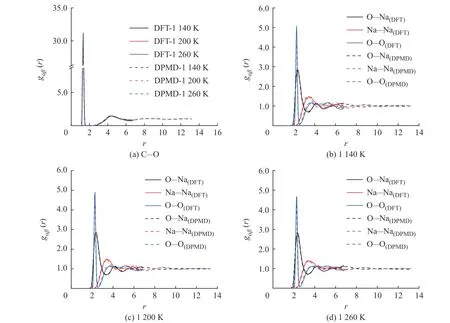
图7 不同温度下Na2CO3 径向分布函数的DPMD 与DFT 计算结果对比Fig. 7 Comparsion of radial distribution functions of Na2CO3 derived from DPMD and DFT calculation at different temperatures

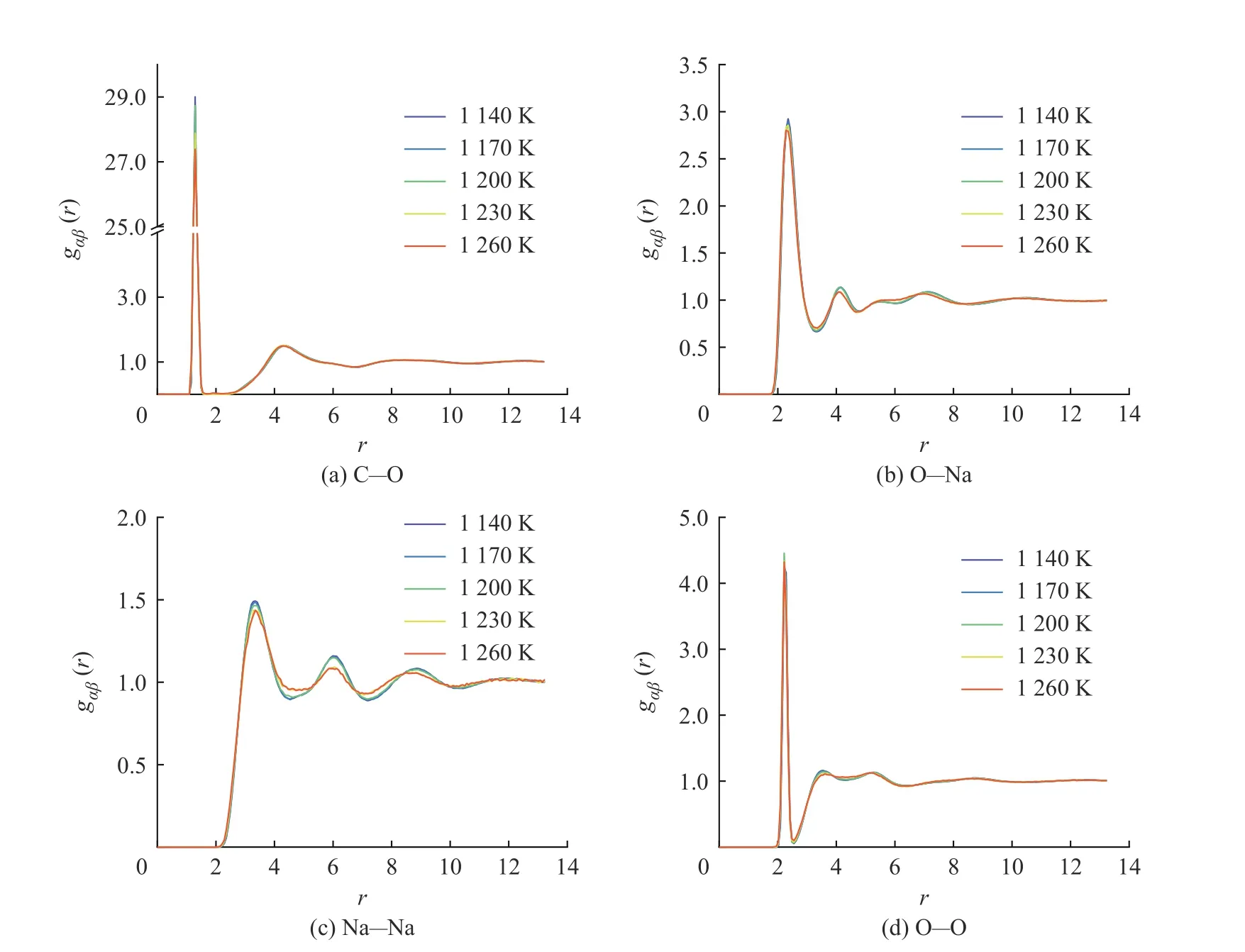
图8 DPMD 方法计算所得的Na2CO3 径向分布函数Fig. 8 Radial distribution functions of Na2CO3 calculated by DPMD method

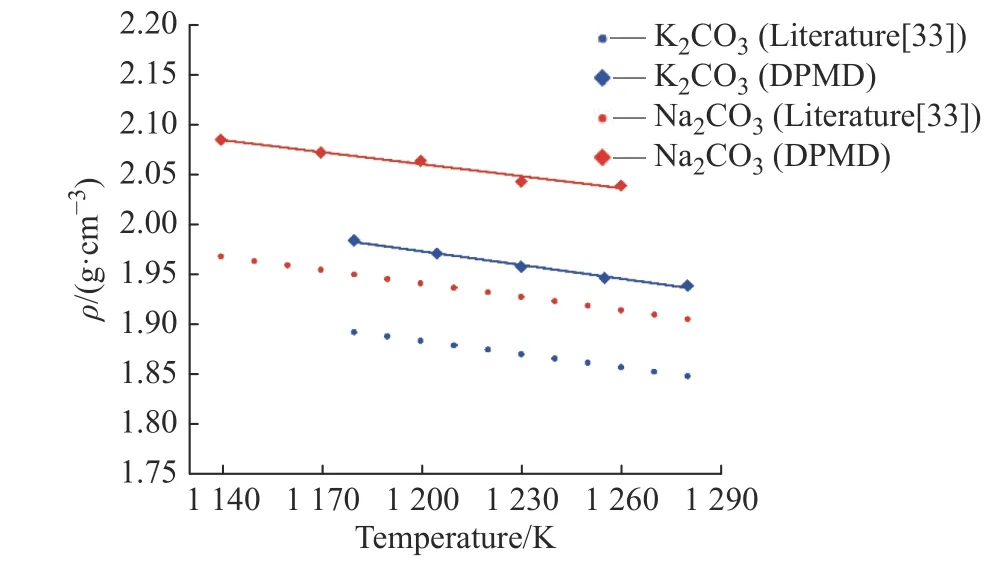
图9 不同温度下K2CO3 和Na2CO3 密度的文献值与模拟值对比Fig. 9 Comparison of literature and simulated density of K2CO3 and Na2CO3 at different temperatures

2.3.2 比热容 根据公式(10)，K2CO3和Na2CO3的温度-焓曲线如图10 所示，曲线斜率即温度区间内的比热容，该比热容为温度区间内的平均比热容。K2CO3和Na2CO3的平均比热容与文献值[33]统计于表1 中，计算偏差分别为3.3%和6.0%。

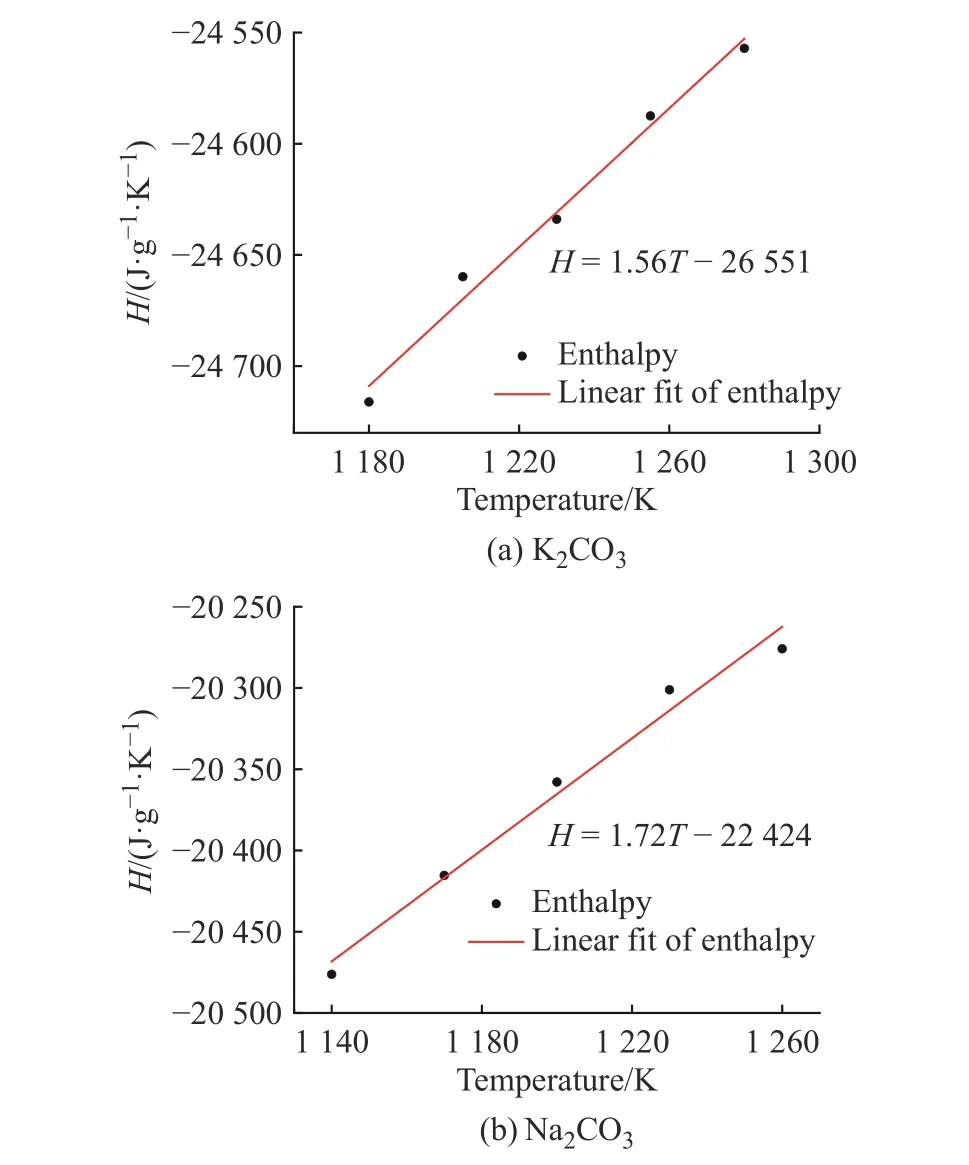
图10 K2CO3 和Na2CO3 计算中焓随温度的变化Fig. 10 Changes of enthalpy of K2CO3 and Na2CO3 with temperature

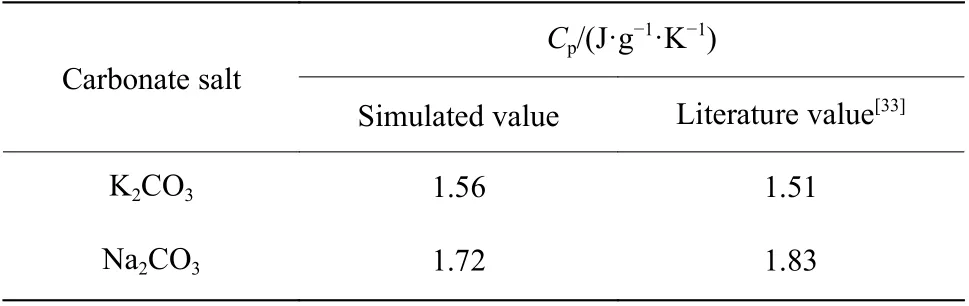
表1 K2CO3 和Na2CO3 比热容的模拟值与文献值对比Table 1 Comparison of simulated and literature values of the Cp of K2CO3 and Na2CO3

2.3.3 热导率 图11 示出了K2CO3和Na2CO3热导率的文献值[34]与模拟值对比，其热导率计算偏差分别约为8.0%和3.5%。从计算点拟合的趋势线发现，K2CO3和Na2CO3的热导率随着温度的升高而降低，在热量传递过程中，粒子只需要在局域范围内振荡，且只需与相邻的粒子发生作用而不涉及长程运动，随着温度升高，体系的摩尔体积增大，离子间距增大，影响了体系通过离子振动传递能量的能力，导致随着温度升高热导率变小。

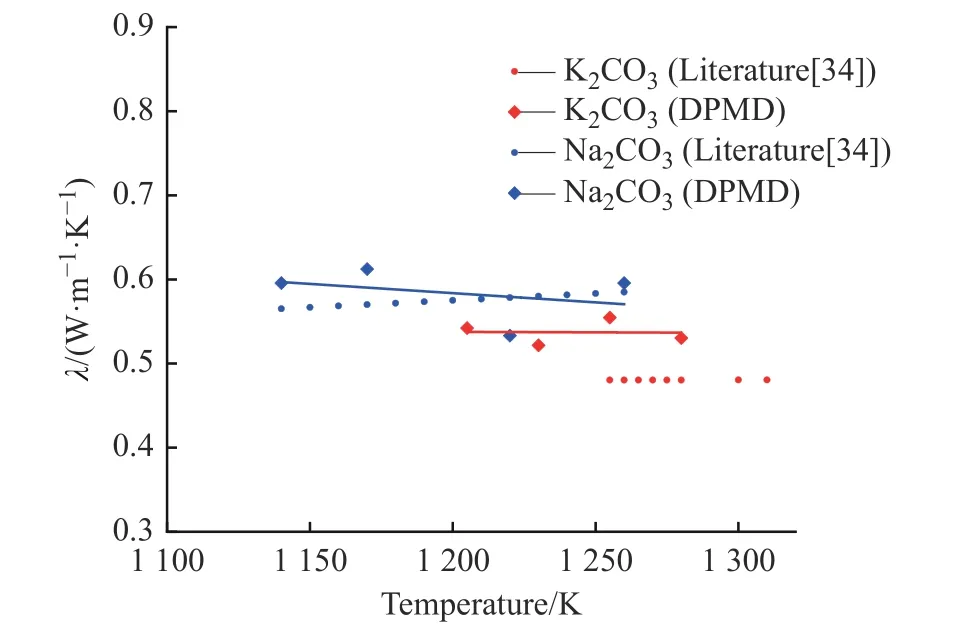
图11 K2CO3 和Na2CO3 热导率的文献值与模拟值对比Fig. 11 Comparison of literature and simulated thermal conductivity of K2CO3 and Na2CO3

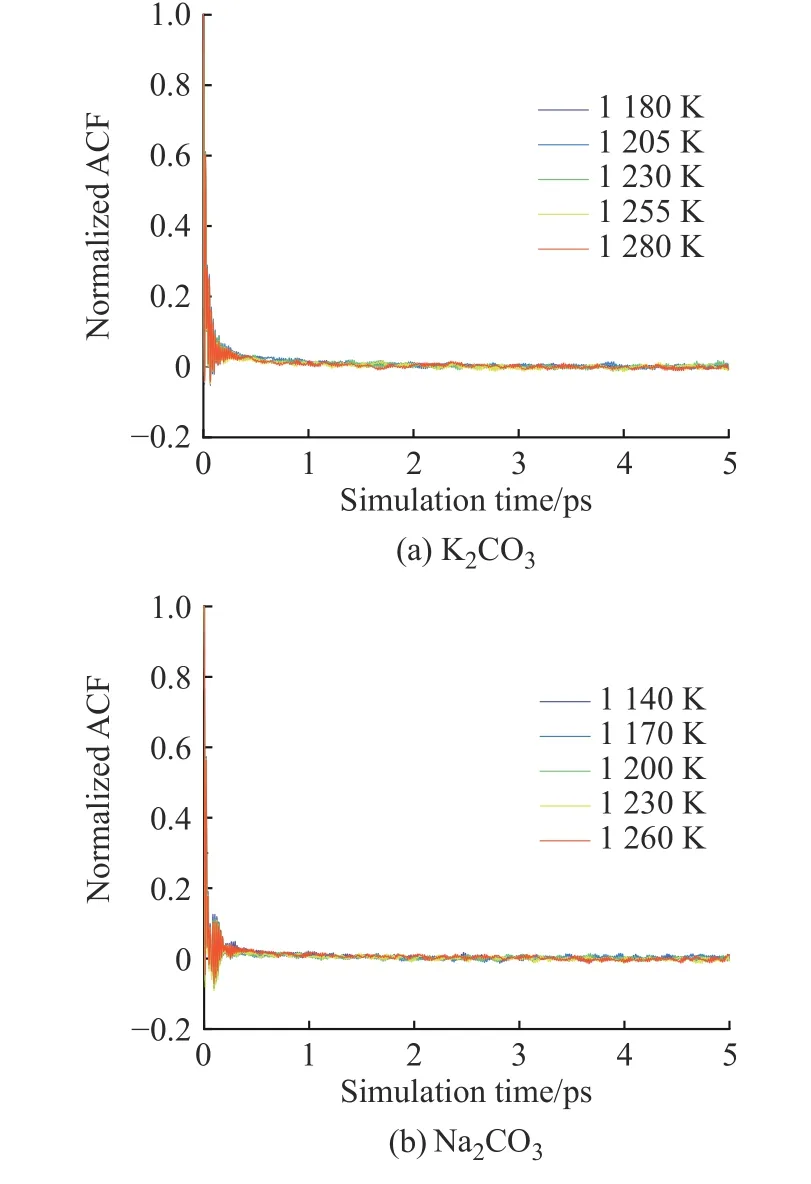
图12 K2CO3 和Na2CO3 归一化张量自相关函数Fig. 12 Normalized stress tensor auto-correlation function of K2CO3 and Na2CO3

2.3.4 黏度 K2CO3和Na2CO3的黏度采用平衡分子动力学模拟方法计算。图12(a)、12(b)分别示出了用Green-Kubo 方法计算K2CO3和Na2CO3的归一化张量自相关函数(ACF)。在模拟时长为5 ps 时，ACF趋近于0 并保持稳定，说明5 ps 的计算时长完全可以满足EMD 方法计算黏度的要求。图13 示出了K2CO3和Na2CO3黏度的文献值[33]与模拟值的对比。由图可知，所得的计算黏度随着温度的升高而降低，并且在温度较高的区域与文献值比较接近。

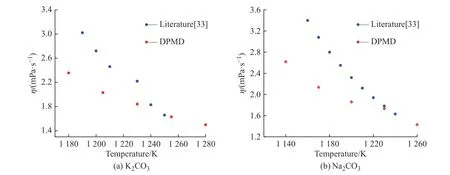
图13 K2CO3 和Na2CO3 黏度的文献值与模拟值对比Fig. 13 Comparison of literature and simulated viscosity of K2CO3 and Na2CO3

3 结 论

（1）采用基于机器学习的分子动力学模拟方法，对碳酸熔盐的微观结构进行了研究。利用第一性原理的计算结果作为训练深度势的数据集，通过DNN训练深度势函数，机器学习为快速获得准确的势函数提供了可靠的方法。

（2）K2CO3的能量和受力的均方根误差分别为8.62×10-4eV和4.67×108eV/m，Na2CO3的能量与受力的均方根误差分别为1.19×10-3eV 和5.31×108eV/m。在结构计算中，DPMD 与DFT 的计算结果吻合较好，说明DPMD 对DFT 有良好的继承性。DPMD 计算结果表明碳酸根为一个整体存在于碳酸盐中，升高温度会造成碳酸根团簇的松散但不会破坏其正三角形结构，同时升高温度会造成阳离子与碳酸根的间距增大，使整个体系的体积增大。在结构计算中，对比K2CO3和Na2CO3性质的模拟值与文献值后发现数据较为接近，K2CO3的密度、比热容和热导率的计算误差分别约为5.0%、3.3%和8.0%；Na2CO3的密度、比热容和热导率的计算误差分别约为5.6%、6.0%和3.5%。

（3）本文的计算证明DPMD 在液态熔盐中的应用是可靠的，深度势函数不仅继承了DFT 的精确性，而且将计算范围从DFT 的温度点扩展到了CMD 的温度范围。这意味着DPMD 摆脱了经验参数的束缚，可以实现高精度、高效率、大尺寸和长时间的模拟。