美国数学月刊第12154 号问题的加强与反向不等式
2022-08-28 01:32:16福建师范大学数学与统计学院杨标桂邮编350117
中学数学教学 2022年4期
福建师范大学数学与统计学院 杨标桂 (邮编:350117)
关键字 几何不等式;美国数学月刊;旁切圆半径
1 问题的提出
Martin Lukarevski[1]在《美国数学月刊》的2020年第1 期提出了如下问题:
定理1(12154号问题)设ra、rb、rc、R、r分别是△ABC的顶点A、B、C所对的旁切圆半径,外接圆半径与内切圆半径,则有
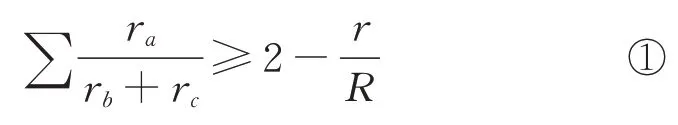
其中∑ 表示循环和.
本文给出不等式①的加强及反向不等式:
定理2设ra、rb、rc、R、r分别是△ABC的顶点A、B、C所对的旁切圆半径,外接圆半径与内切圆半径,则有
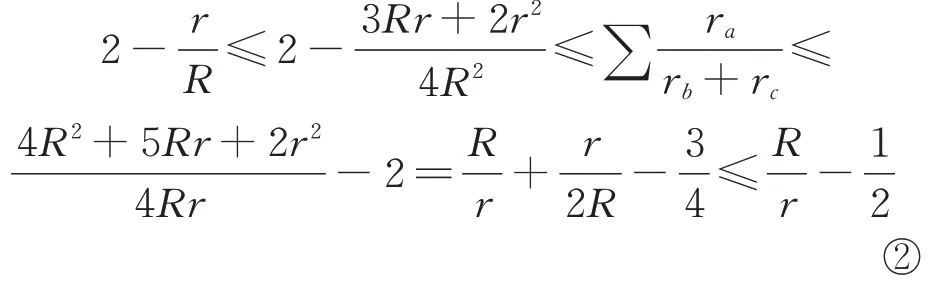
2 几个引理
为了证明定理2,我们给出一些关于三角形的各种半径和半周长的恒等式与不等式:
引理1设ra、rb、rc、R、r、s分别是△ABC的顶点A、B、C所对的旁切圆半径,外接圆半径,内切圆半径与半周长,则有

其中∏f(a,b,c)表示循环积.
证明③~⑥是熟知的结论.令∑ra=ra+rb+rc=4R+r=X,于是

引理2设ra、rb、rc、R、r、s分别是△ABC的顶点A、B、C所对的旁切圆半径,外接圆半径,内切圆半径与半周长,则有
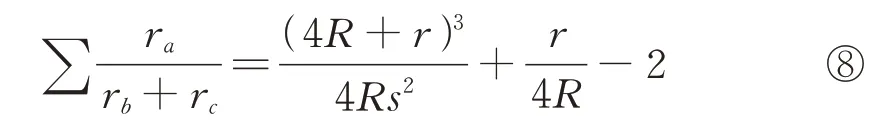
证明令∑ra=ra+rb+rc=4R+r=X,由引理的③~⑦,可得

因此,引理2 得证.
下面在给出一个关于三角形的半周长的双向不等式:
引理3设R、r、s分别是△ABC的外接圆半径,内切圆半径与半周长,则有
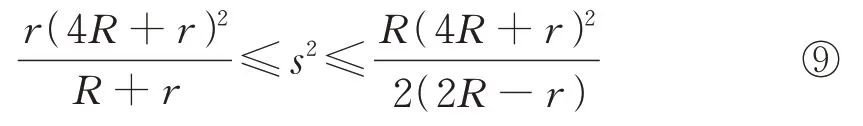
⑨的右边不等式就是著名的Kooi 不等式.
3 定理的证明
定理2 的证明由恒等式⑧和不等式⑨,有
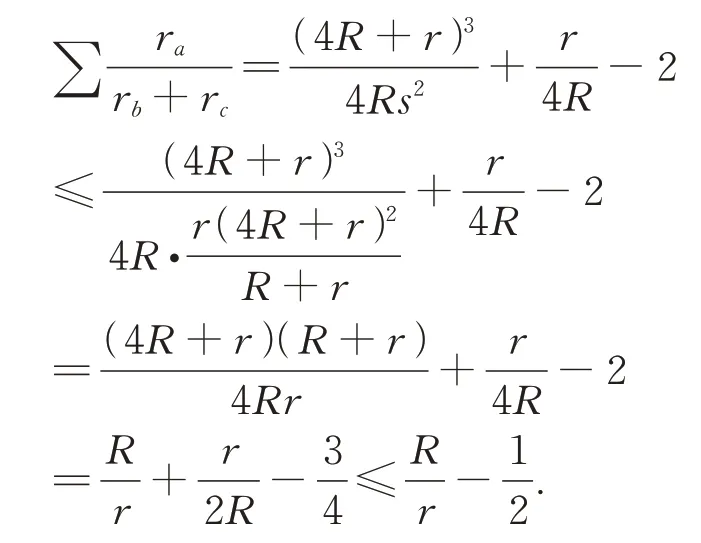
最后一个不等号利用了Euler 不等式.
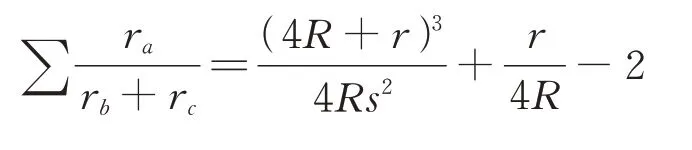
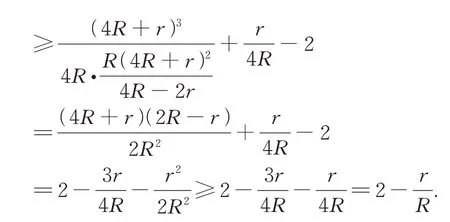
最后一个不等号利用了Euler 不等式,因此定理2 获证.
类似地,还可以得到一个简单的不等式:
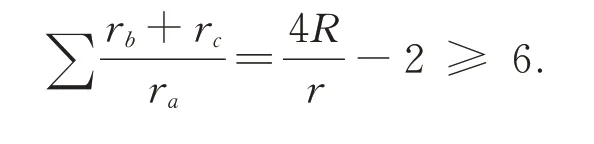
猜你喜欢
中等数学(2021年2期)2021-07-22 06:21:52
中等数学(2020年9期)2020-11-26 08:07:28
中学数学教学(2019年3期)2019-06-21 08:10:52
中等数学(2018年8期)2018-11-10 05:07:22
中等数学(2018年7期)2018-11-10 03:29:04
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
初中生世界·七年级(2016年6期)2016-05-28 21:26:29
初中生世界·七年级(2016年6期)2016-05-28 19:34:14
中学生数理化·七年级数学人教版(2016年5期)2016-05-14 13:56:12
小雪花·成长指南(2014年9期)2014-10-20 12:29:15

