不同排涝情景下泵站单机组变角优化运行研究

陶旭辉，仇锦先，阚永庚

（1.扬州大学水利科学与工程学院，江苏扬州 225009；2.江都水利工程管理处，江苏扬州 225200）

0 引 言

近年来，由于气候异常引起的自然灾害频繁发生，特别是短历时暴雨或持续性降水往往引起洪涝灾害［1，2］。若区域性涝水不及时排出，则会对当地的生产、生活和生命财产安全造成危害或损失。据统计，暴雨洪涝损失约占全球各种自然灾害损失的40%［3］。而排涝泵站是区域涝水及时排出的重要设施，如何提高汛期排涝泵站排水效率或节省耗能，已引起国内外学者的关注，并开展了相关理论研究与应用。

Fecarotta 等［4］构建了排涝泵站能耗最小的混合整数优化模型，并应用于意大利那不勒斯城市排水系统，平均节省32%的能耗；Yazdi 等［5］考虑降雨事件的随机性，通过耦合一个数学模型和一种新的混合和声搜索算法，获得了排涝泵站最优运行策略，并应用于实际城市排水系统，有效提高了排水效率。袁丹青等［6］构建了以全年排涝耗能最小为目标、以受涝时间和涝水位为约束的数学模型，实现了排涝泵站的最优调度；张礼华等［7，8］分别构建了以开机机组总耗能最少和能耗率最低为目标，以及机组运行费用最少为目标的优化模型，实现了特定排水标准下的排涝泵站最优运行；吴远为等［9］构建了以耗电量最低为目标、以排水量和功率等为约束的站内优化调度模型，得到了排涝泵站较好的优化调度方案；刘静森等［10，11］提出排涝泵站群总能耗最小的多方案试验选优、圩区外河水位控制去劣的优化运行调度方法，有效降低了城镇圩区排涝泵站群日常运行能耗；高玉琴等［12］构建了圩区排涝泵站等功耗下排水量最大的优化调度模型，有效提高了排涝泵站除涝效率；张浩等［13］以排涝效果最佳为目标，通过多机多种运行模式组合数值模拟，获得了排涝效果最佳、河道和航运安全影响最小的运行方案。

上述研究数学模型大部分是以排涝泵站耗能最小或排水量最大为单目标的优化问题，本文针对不同排涝标准（日常排涝、超标准排涝）、不同排涝阶段（预降阶段、抢排阶段）等实际情况，拟构建综合考虑排水量最大、耗电费用最小的多目标优化数学模型。同时，考虑到泵站机组不宜频繁启停，所以在优化模型中拟增加文献尚不多见的停机次数作为约束条件，以期最终的优化结果更具有可操作性，更符合排涝泵站实际运行情况。

1 优化模型构建与求解

1.1 目标函数

针对变角运行的排涝泵站单机组，考虑汛期不同排涝标准、不同排涝阶段的实际要求，以规定时间内排水量最大、耗电费用最低为多目标函数，以机组运行功率、叶片安放角度、停机次数等为约束条件，构建综合考虑排水量和耗电费用的非线性多目标排涝泵站单机组变角优化数学模型。

式中：W 表示一个排涝周期内最大排水总量，万m3；i表示时段，i=1，2，…，n（时段总数）；θij表示第i 时段第j 个叶片角度离散取值表示第i 阶段第j 个角度所对应的排涝流量，m3/s，扬程一定时其是θij的函数，不开机时为0；ΔTi为第i 时段时间长度，h；F为一个排涝周期内耗电费用，元；Hi为第i时段平均排涝扬程，m；Pi为第i时段分时电价，元（/kWh）；ηzi、ηmot、ηint分别表示第i 时段泵装置效率（根据泵装置Q～η 性能曲线确定）、电动机效率和传动效率。

1.2 约束条件

（1）叶片安放角度约束。

式中：θmin、、θmax分别表示叶片安放角度的最小值与最大值。

（2）运行功率约束。

式中：Ni(θi)表示第i 时段机组实际运行功率，kW；Ne表示机组电机额定功率，kW。

（3）停机次数约束。

式中：u、umax分别表示一个排涝周期内机组运行实际停机次数和允许最大停机次数。

1.3 模型求解

上述构建的两个目标函数（排水量最大、耗电费用最小）存在一定的矛盾冲突，而当各个目标函数处于冲突状态时，就不会存在使所有目标函数同时达到最大或最小值的最优解，通常只能寻求一组非劣解。为了求得多目标规划问题的非劣解，又常常需要将多目标规划问题转化为单目标问题去处理。文献［14］也提出“在多目标优化的情况下，特别是当各个目标之间有矛盾冲突时，可以先控制一些目标然后使另一个目标达到最大（最小）化”。因此，考虑到排涝泵站两目标重要程度不同（抓住主要目标、兼顾次要目标），选择排水量最大作为主要目标，而耗电费用最小只要满足一定的控制要求，将其转换成约束条件，即将多目标优化模型转化如下单目标优化模型求解：

为得到一系列不同耗电费用下各时段决策方案及最大排水量，供泵站管理部门在不同排涝情景下决策参考，这里采用一维动态规划法［14］进行模型的求解。以时段作为阶段变量，以叶片安放角度作为决策变量，以耗电费用作为状态变量，各阶段状态转移方程、系统递推方程如下：

（1）阶段i=1：

状态变量λ1在其可行域［f1，1，f1，m］内离散：λ1= f1，1，f1，2，f1，3，…，f1，m，其中f1，1、f1，m分别表示第1 阶段开机时的最小费用与最大费用；m表示按等步长离散的个数。

（2）阶段i（1＜i ＜n）：

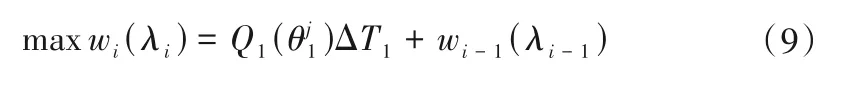
状态变量λi在其可行域［fi，1，fi，m］内离散：λi= fi，1，fi，2，fi，3，…，fi，m，其中fi，1表示第1～i 阶段均开机时的各阶段最小费用中的最小值；fi，m表示第1～i 阶段均开机时的各阶段最大费用之和。

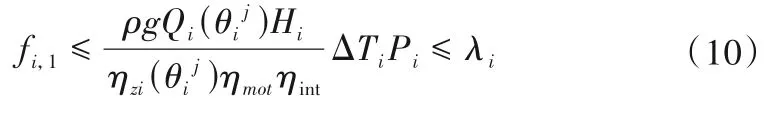
状态转移方程：

（3）阶段n：

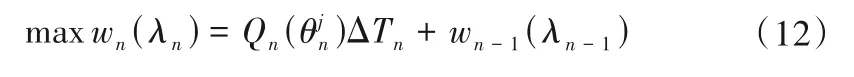
状态变量λn在其可行域［fn，1，fn，m］内离散：λn=fn，1，fn，2，fn，3，…，fn，m，其中fn，1表示n 个阶段均开机时的各阶段最小费用中的最小值；fn，m表示n个阶段均开机时的各阶段最大费用之和。

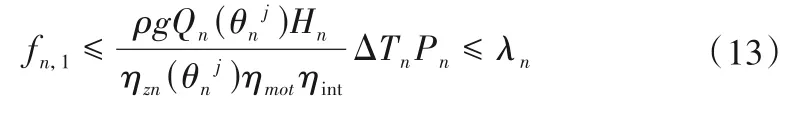
状态转移方程：

2 实例应用与计算结果分析

本文选取某圩区排涝泵站单机组变角优化运行为例，建立以日运行排水量最大和耗电费用最小为多目标的数学模型，采用上述一维动态规划算法、同时辅以Frotran 语言编程求解，可以得到一系列与不同耗电费用所对应的运行方案，包括各时段开停机、叶片安放角度的决策情况，以及一日最大排水量、实际耗电费用和单位费用排水量（即最大排水量除以实际耗电费用，m3/元）。

2.1 基本参数说明与确定

（1）时段划分与分时电价。根据汛期排涝泵站一天内扬程变化情况，结合江苏省峰谷电价时段划分，将一天划分为9个计算时段。具体时段划分与分时电价见表1。

表1 各时段内平均扬程及分时电价Tab.1 Average head and time-of-use price in each period

（2）时段内平均扬程。该圩区汛期警戒水位为2.0 m，根据圩区多年汛期排涝运行情况，当内河水位上升到1.8 m，且天气预报仍有强降雨过程，则开机排涝预降水位，圩区内河水位一般呈现先降、后升再降的变化过程，而外河水位相对变化不大（一般6.2 m 左右）。以该圩区某一设计频率的来水过程为例，排涝泵站一天内不同时段平均扬程如表1所示。

（3）流量和装置效率。排涝泵站的机组型号为2000ZLQ1 3.7-7.8，额定转速为214.3 r/min，设计叶片角度为+2°。在排涝泵站变角运行情况下，根据水泵不同叶片安放角度（-6°、-4°、-2°、0°、+2°、+4°）时的Q～H、Q～η性能曲线，结合时段平均扬程，可确定各时段不同角度时的排涝流量和装置效率［15］。

2.2 计算结果分析

大型泵站不宜频繁停机，否则会缩短机组使用年限，增加设备维修费用，甚至危及泵站运行安全。本文考虑停机次数对变角优化运行结果的影响，分别分析无停机约束、停机次数0次约束和1 次约束3 种情况下，不同耗电费用下的最大排水量及单位费用排水量变化规律，见图1～3。其中，超标准排水或抢排阶段以不停机考虑，即停机次数为0；预降阶段考虑停机次数不超过1次；日常排水不考虑停机次数约束。

图1 无停机次数约束下最大排水量及单位费用排水量变化情况Fig.1 The variation of maximum drainage and unit cost drainage（not considering the constraint of shutdown times）

（1）无停机次数约束下最大排水量及单位费用排水量变化情况如图1 所示。由图1 可知，不同耗电费用下的最大排水量总体上呈上升趋势，其中耗电费用0.2～1.0 万元（最大耗电费用的10%～50%）区间上升趋势较为明显，即增加相同数量费用，提水量增加幅度较大；耗电费用1～2 万元（最大耗电费用的50%～100%）区间最大排水量上升幅度减缓，曲线较为平缓。另外，不同耗电费用下的单位费用排水量曲线总体呈下降趋势，以耗电费用1 万元（最大耗电费用的50%）为界，右边单位费用排水量曲线段下降较为平缓，而左边曲线段下降较快，这表明在低费用阶段（小于最大耗电费用的50%），排水总量虽然处于较低水平，但单位费用排水量处于较优的状态，即单位费用可排出较多的水量，这适用于排水量不多、兼顾节省能耗的日常排水。

（2）在不停机（停机次数为0）约束下最大排水量及单位费用排水量变化情况如图2所示。当圩区发生超标准降水或内河水位超出警戒水位，排涝泵站投入抢排阶段，此时机组考虑不停机而连续运行，使内河水位尽快降至安全水位，以保证区域免受涝灾。本实例当机组一天内不停机时最低耗电费用为14 861.0 元，故这里选取耗电费用1.5～2.0 万元作为分析区间。由图2可知，最大排水量随耗电费用增加而增加，但增加的幅度表现为曲线先陡后缓；这从单位费用排水量曲线也可以看出，耗电费用1.50～1.65 万元区间单位费用排水量呈上升趋势，而1.65～2.00 万元区间呈下降趋势。同时，耗电费用1.6～1.7 万元（最大耗电费用的80%～85%）区间单位费用排水量较大，是多目标（提水量尽可能多、耗电费用尽可能少）均较优的区间，此区间最大排水量约为耗电费用2 万元时最大排水量的85%～90%。

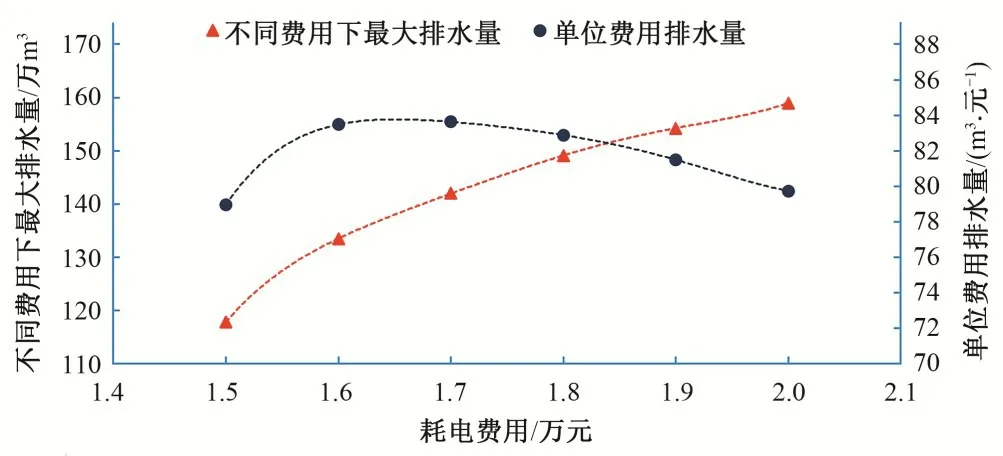
图2 不停机约束下最大排水量及单位费用排水量变化情况Fig.2 The variation of maximum drainage and unit cost drainage（considering the constraint of“shutdown times”=0）

（3）根据无停机约束条件下不同耗电费用下最大排水量的计算结果可知，一个排涝周期内间断性的停机次数一般不超过2次（这里指不相邻的阶段停机次数累加值，若计算中出现相邻阶段连续停机，则停机次数按1 次考虑），结合排涝泵站运行的实际情况，将停机次数约束取1 次为宜。由图3 不同费用下最大排水量曲线可以看出，总体上最大排水量随耗电费用增加而呈上升趋势。当耗电费用在0.6～1.2 万元（最大耗电费用的30%～60%）区间时，由程序计算结果可知，无停机约束时停机次数超过1 次（如表2 所示），而考虑停机次数约束时，因受停机次数≤1影响，在动态规划寻找最优路径时需作出调整。从图中趋势线水平段可以看出，受约束条件影响耗电费用在此区间时的实际耗电费用和最大排水量均与0.6 万元时一致。另外，单位费用排水量曲线总体上则呈下降趋势，同样受停机次数约束影响中间段曲线呈水平趋势。因此，当耗电费用有保证且排涝处于预降阶段时，考虑停机次数≤1 的约束条件，建议在耗电费用1.2～2.0 万元（最大耗电费用的60%～100%）区间变角优化运行，此时可获得较多的排涝水量。

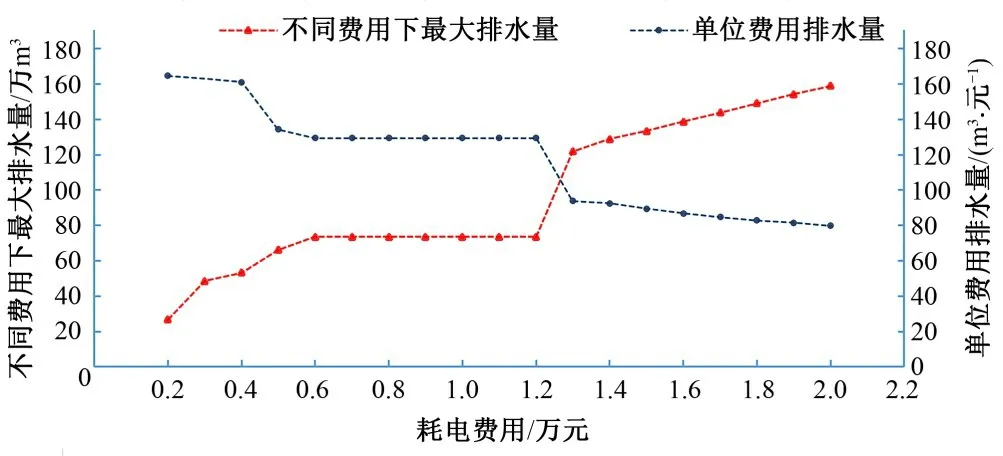
图3 停机次数≤1约束下最大排水量及单位费用排水量变化情况Fig.3 The variation of maximum drainage and unit cost drainage（considering the constraint of“shutdown times”≤1）

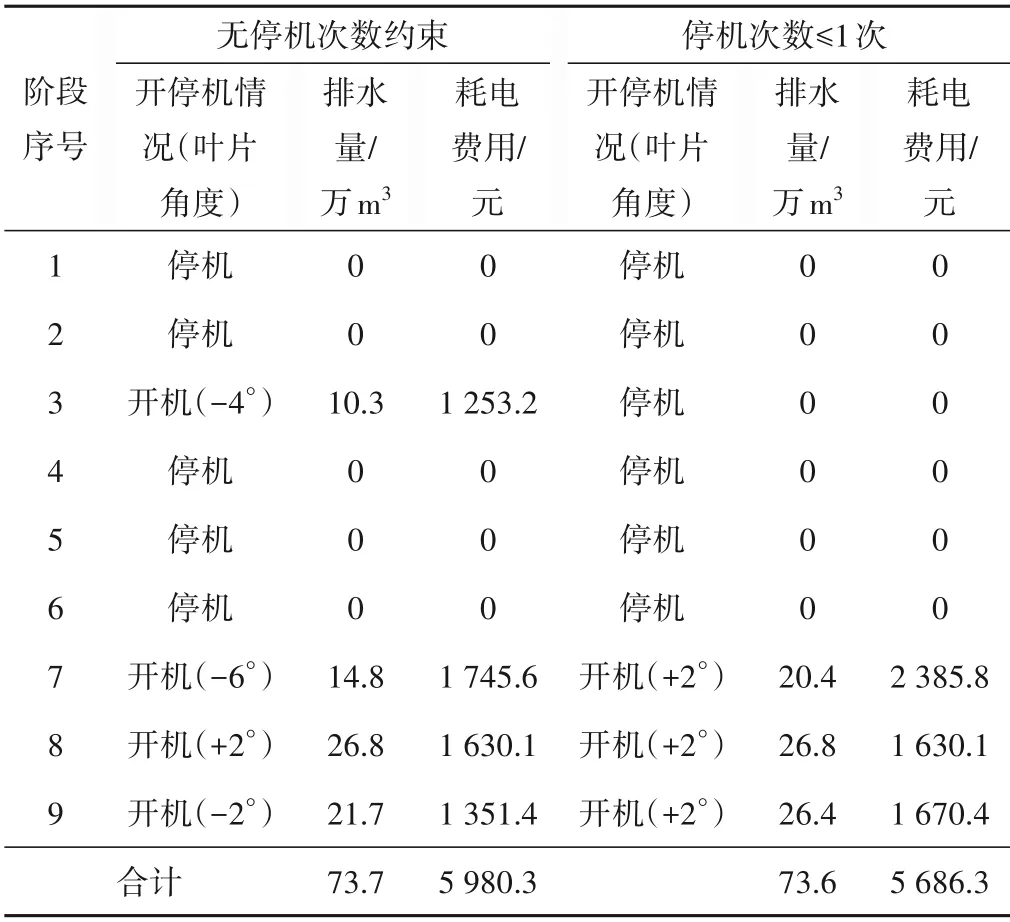
表2 停机次数对优化结果的影响（以耗电费用≤6 000元为例）Tab.2 Influence of shutdown times on optimization results（taking“power consumption cost”≤6 000 yuan as an example）

3 结 论

本文综合考虑排涝泵站的排水量与耗电费用，构建了非线性多目标单机组变角优化数学模型，选取某排涝泵站日运行为例，分析了单机组在不同排涝情景下的计算结果，并对汛期排涝泵站优化运行提出了建议。主要结论与补充说明如下：

（1）根据无停机次数约束下变角优化运行最大排水量及单位费用排水量分析，当给定耗电费用小于最大耗电费用的50%，排水总量虽然处于较低水平，但单位费用排水量处于较优状态，即单位费用可排较多水量，这适用于排水量不多、且考虑能耗节省的日常排涝。

（2）根据不停机约束下变角优化运行最大排水量及单位费用排水量分析，当给定耗电费用在最大耗电费用的80%～85%区间时单位费用排水量较大，且排水量约为最高费用所对应的最大排水量的85%～90%，是排水总量、耗电费用均较优的区间，这适用于不考虑停机而连续运行的超标准排涝或抢排阶段。

（3）根据停机次数≤1约束下变角优化运行最大排水量及单位费用排水量分析，当耗电费用有保证时，且排涝处于预降水位阶段，可考虑停机次数≤1 的约束条件，并建议在最大耗电费用的60%～100%区间变角优化运行，可以保证较多的排水总量。

（4）实例得到了一系列与不同耗电费用所对应的各时段开停机、叶片安放角度的决策方案，以及相应的最大排水量。在实际应用时，可根据不同排涝情景下预估的排水量，选择相应的决策方案。

（5）构建的数学模型适用于单机组变角优化运行问题，若是多机组变角优化运行，在模型中还要增加开机台数这一决策变量。关于多机组排涝泵站变角优化问题，将作为后续进一步开展研究的内容。