基于改进粒子群算法的泵站优化运行研究

晏 毅，赖喜德，陈小明，谭祺钰，刘雪垠，宋冬梅

（1.西华大学能源与动力工程学院，成都 610039；2.四川省机械研究设计院（集团）有限公司，成都 610063）

0 引 言

泵在工业及民生领域有着广泛的应用，每年泵的电耗占总电耗的20%以上［1］。在实际条件下，因泵工作在低效区域，造成泵可靠性降低，影响正常生产过程［2］。因此，通过优化控制对降低泵站能耗、提升泵运行稳定性有着重要意义［3］。

泵站优化运行是多目标和多约束的复杂优化问题，近年来，针对泵站优化运行问题，一些研究人员在算法改进上开展了工作，王圃等［4］提出交叉变异的自适应全局最优引导人工蜂群（ABC）；冯晓莉等［5］将模拟退火引入狼群（WPA）算法，并对WPA 算法参数进行优选。以上研究在泵站优化运行中取得良好效果，明显降低泵站系统能耗。粒子群（PSO）［6］算法因初始参数较少，实现简单，收敛快而被广泛应用于电网运行、泵站运行等实际工程应用，但PSO 算法在收敛速度较快的同时容易陷入局部优解；同时迭代后期收敛精度不高，其局部搜索能力还有待提升。为求解泵站优化运行问题，提出一种改进PSO 算法，该算法对惯性权重进行改进，使传统PSO 算法控制参数自适应变化，同时借助模拟退火与柯西变异的提高算法全局搜索能力及收敛精度。通过测试函数验证了改进PSO 算法的性能，并将其应用于实际工程问题，为供水泵站优化运行问题提供了一个解决方案。

1 泵站优化运行的数学模型

以某供水泵站为研究对象，该泵站各泵以并联方式运行。泵站系统优化运行通过对泵站各泵进行优化控制，保证用户用水需求，提高泵站运行效率，减小泵站运行成本。因此，本文以最小输入功率为目标，并满足相关约束条件，建立泵站优化运行数学模型。

1.1 水泵外特性参数化

水泵外特性曲线参数化是建立泵站优化运行数学模型的基础，对泵流量-扬程曲线进行指数拟合［7］，对流量-功率曲线进行二次多项式拟合。并结合离心泵相似定律［8］，得到任意转速下的离心泵外特性曲线方程如下：

Q-H曲线：

Q-P曲线：

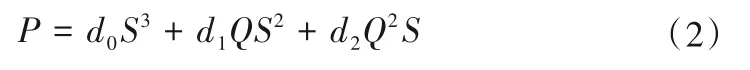
1.2 数学模型

假设供水泵站共配置了n台水泵，其中有m台为调速泵，其余为定速泵。

定义状态因子W，W =[W1，W2，W3，…，Wn]，Wi表示第i台泵的工作状态（1-工作，0-不工作）。

定义调速因子S，S =[S1，S2，S3，…，Sm]，Si表示第i 台调速泵的调速比。

系统管阻特性曲线：

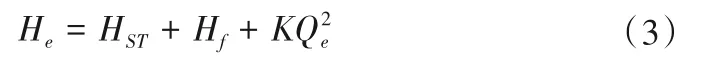
式中：HST为管网末端用户所需扬程；Hf为管网静扬程损失；K 为管阻系数；Qe为所需流量；He为满足供水指标而应提供的扬程。

在系统给定扬程需求后，由泵的并联特性曲线与管网特性曲线的交点可确定水泵工况点。

1.2.1 目标函数

以泵站总输入功率最小作为目标函数，使用外罚函数对约束条件进行无约束处理。目标函数可表示为：

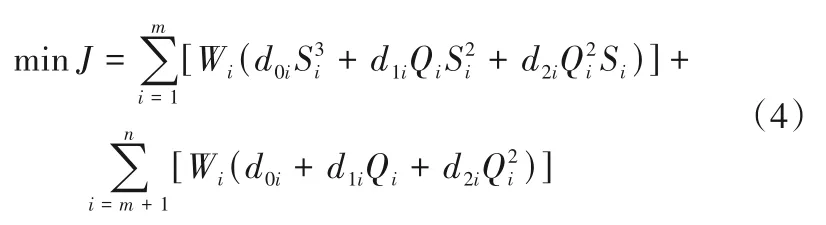
式中：J为泵站总输入功率；Qi为第i台水泵的流量。

1.2.2 约束条件

（1）总流量约束：水泵并联时，总流量为各台泵流量之和，通过式（1）反解流量Q有：

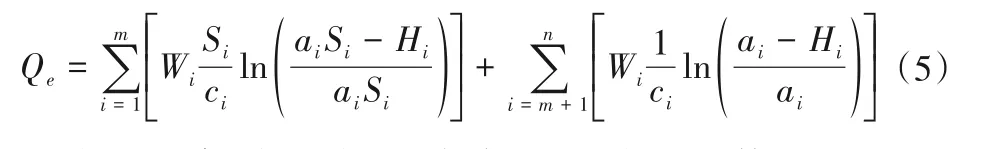
（2）扬程约束：水泵并联时各台泵出口扬程相等，即：

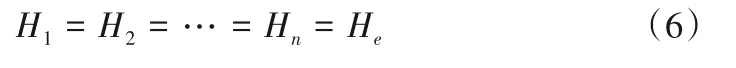
（3）调速比约束：为了稳定工作和防止汽蚀，通常调速泵具有最低运行速度限制。本文定义调速比约束为Si∈[Simin，1]。

（4）单台泵流量约束：为了保证水泵的高效运行定义泵高效区如图1所示。

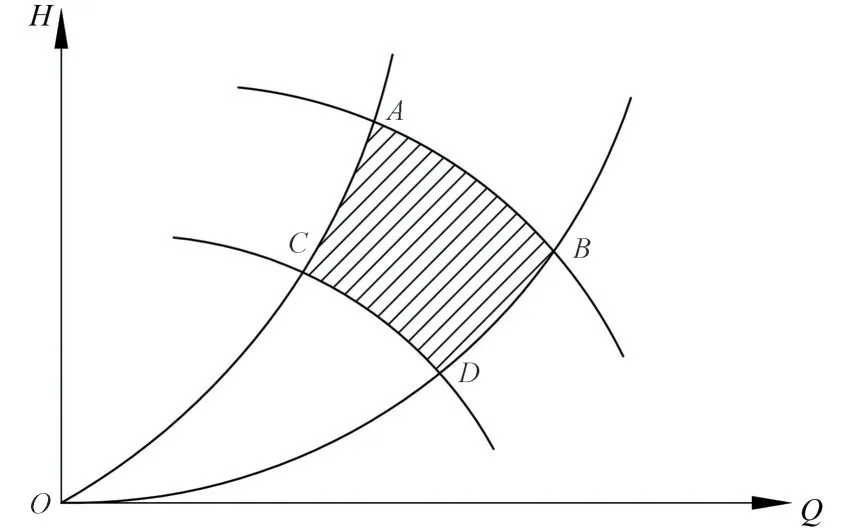
图1 变频泵高效区Fig.1 High efficiency zone of variable frequency pump

其中曲线段AB 定速泵的高效区，曲线AB、CD 和相似工况抛物线OA、OB所围成的扇环区域为调速泵的高效区。

相似工况抛物线OA为：

相似工况抛物线OB为：

由式（1）、（7）、（8）可得：

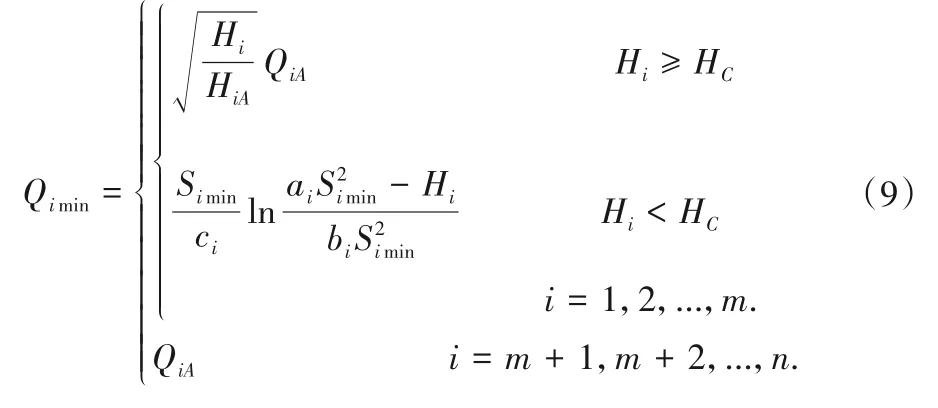
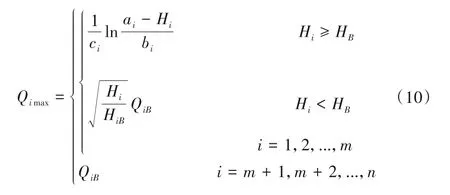
式中：Qimin，Qimax为第i 台水泵水泵高效区边界上的点，第i 台水泵的流量约束可表示为：

2 优化求解算法

2.1 基本粒子群算法

粒子通过对上一次速度的继承、自身及种群最优位置的共同作用完成一次寻优。其速度与位置更新如下：

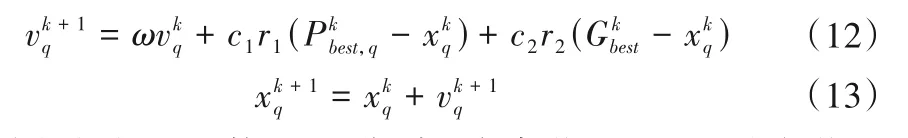
式中：ω为惯性权重系数；c1、c2分别是自身学习因子和社会学习因子分别为第q个粒子在第k次迭代时的位置和速度；r1和r2为rand（0，1）的随机值为第q 个粒子第k 次迭代时历史最优位置为第k次迭代时种群最优位置。

2.2 改进粒子群算法

（1）惯性权重：本文对惯性权重采用一种随迭代次数非线性递减策略。在搜索初期进行全局搜索；中期逐渐加强局部搜索的能力；后期着重局部搜索。惯性权重随迭代次数的变化规律如下：

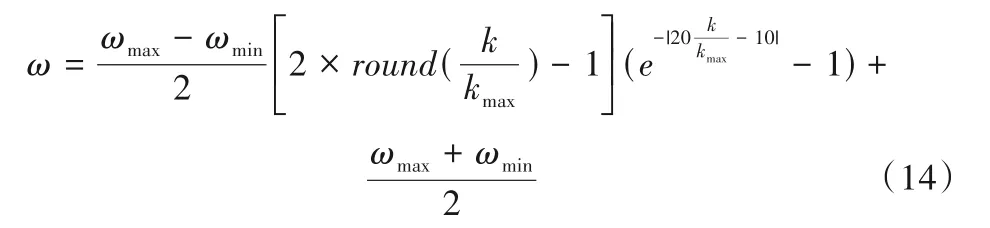
式中：ωmax，ωmin为惯性权重的最大值和最小值；round（）为四舍五入的整数；kmax为最大迭代次数。经实验证明［9］当ωmax=0.95，ωmin=0.4 时算法寻优性能较好。为方便计算，本文取ωmax=0.9，ωmin=0.4。惯性权重随迭代次数变化图像如图2所示。

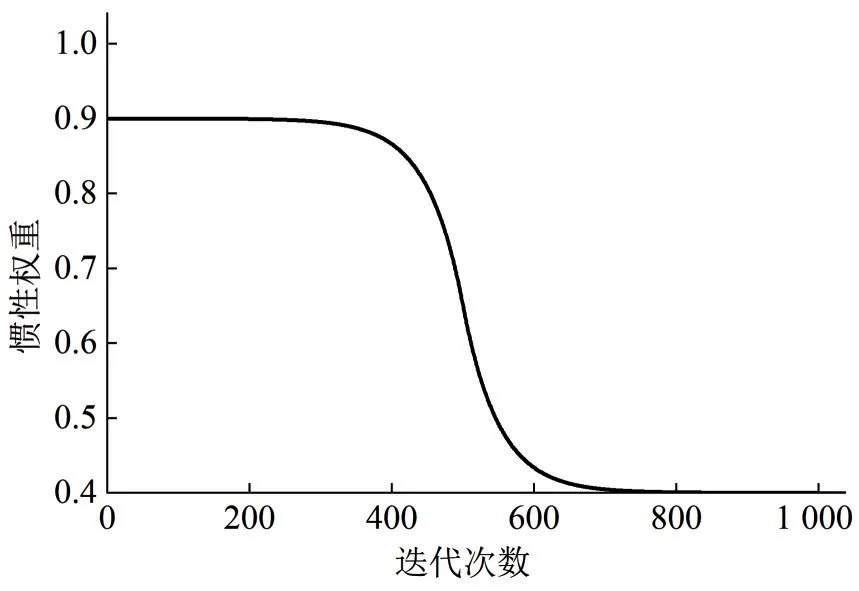
图2 惯性权重变化曲线Fig.2 Change curve of inertia weight

学习因子采用线性递减变化策略：

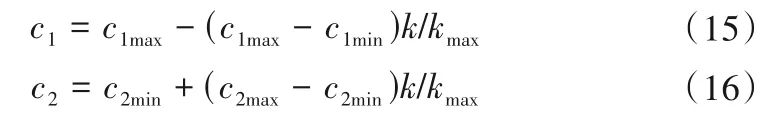
参照文献［12］，取c1max=2.5，c2max=2.5，c1min=1.25 和c2min=1.25。在迭代前期增强全局搜索能力，迭代后期增强局部搜索能力。

（2）加入模拟退火操作：每次迭代根据Metropolis 准则判断是否由干扰产生的新解替代全局最优解，以搜寻最小值为例，其表达式如下：

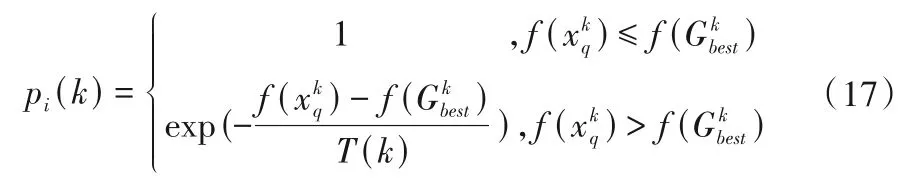
式中：T（k）表示第k次迭代时的温度，温度随每次迭代以一定程度线性衰减。

采用经验法则［10］确定初始温度T0：即选定一个大值作为T0的当前值，若初始接受率小于预定的初始接受p0（当p0处于0.8时性能突出［10］，取p0=0.8），则将当前T0值加倍，以新的T0值重复上述过程，直至得到使p＞p0的T0值。温度变化的具体操作为：

式中：μ为降温系数，一般取0.95～0.99［10］，这里取μ=0.96。

（3）加入柯西变异操作：采用Deb 的运行期收敛指标［11］：经过若干代（如10 代），趋近度ΔCP（定义为|f(Gbest(k) - f(Gbest(k -10)|/f(Gbest(k))）若小于阈值ξCP（一般取0.05～0.1［11］，本文取ξCP=0.05），计算种群各维度变量的多样性，若种群某一维变量的多样性评价指标低于某一阈值，则对种群的该维变量进行如下操作：

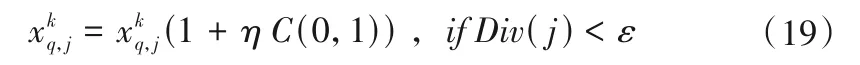
种群多样性的评价形式如下：

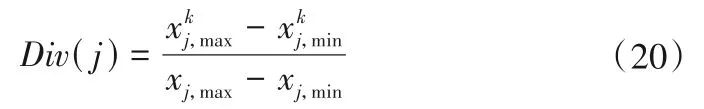
为了提升算法后期局部搜索能力，柯西变异比例系数η 采用随迭代次数线性递减策略，其形式为：

式中：η0为初始比例系数，取η0= 1.5。算法流程图如图3所示。

图3 算法流程框图Fig.3 Algorithm flow chart

2.3 算法的性能测试

选取表1 函数对本文算法性能进行测试，同时与4 种［12-15］改进PSO 算法进行对比分析，在维数D=30、种群规模popsize=30、最大迭代次数kmax=1 000情况下运行30次，其测试结果见表2所示、收敛情况如图4所示。

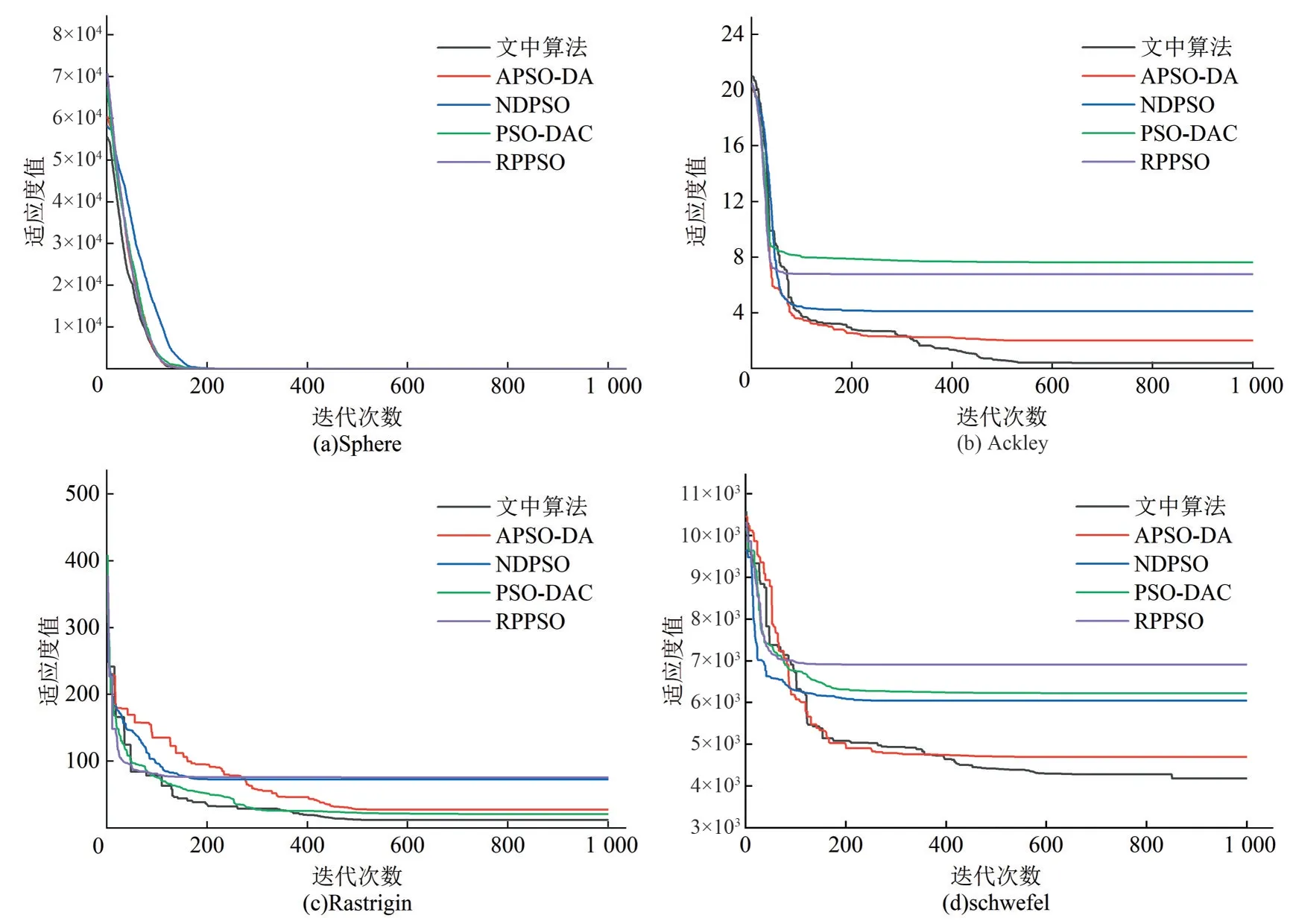
图4 不同测试函数的算法迭代曲线Fig.4 Algorithm iteration curves of different test functions

表1 测试函数Tab.1 Test function

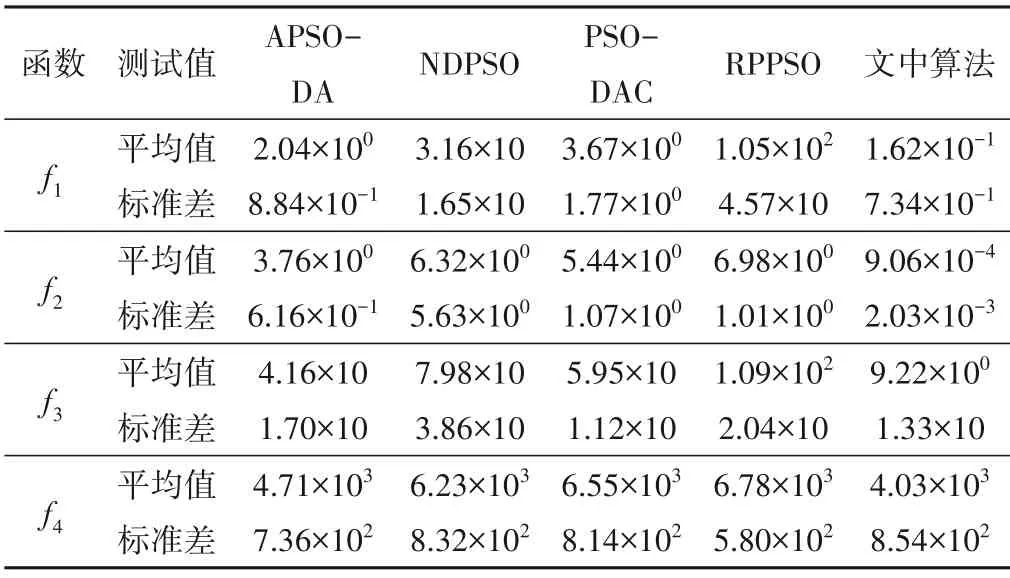
表2 各算法性能测试结果Tab.2 Running results of optimization algorithm

分析测试结果可知，在平均值测试中改进算法的寻优精度相比于参照的算法具有明显优势。在标准差测试中f3不如PSO-DAC 算法，但相差程度不大；f4不如RPPSO 算法，对于其他测试函数为最优，表明算法在搜索稳定性上表现良好。从收敛图可得知算法具有良好的收敛性能，在保证收敛速度的同时局部寻优能力提升较大，对于多峰值、局部优解差值小的f4函数，算法充分发挥了模拟退火及柯西变异的优势，使算法在迭代中后期具有较强的局部搜索能力，提高算法的求解精度。

3 工程实例

3.1 工程概况

某供水泵站各泵采用并联运行方式，现有水泵配置见表3。

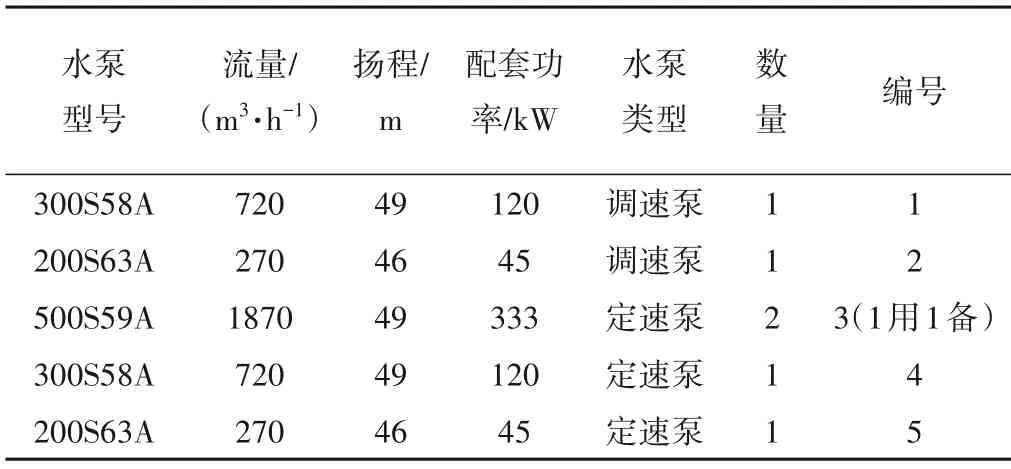
表3 泵站水泵配置情况Tab.3 Pump configuration of pump station

供水泵站供水规模为8 万m3/d，日用水量变化曲线及泵站所需提供扬程如图5所示。

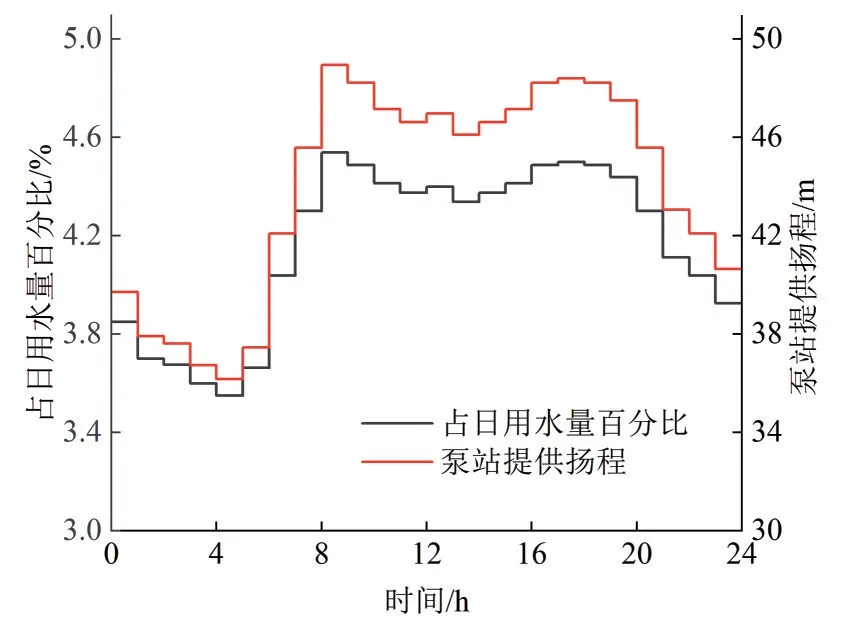
图5日流量及扬程变化曲线Fig.5 Daily flow and head change curve

泵站工作人员根据供水曲线对各泵进行启停控制，各泵随时间变化的启停情况如表4所示。该泵运行费用采用国家标准进行分时计价，其中电费基价为0.617 元/kWh，日消耗运行费用为9 252.37 元。

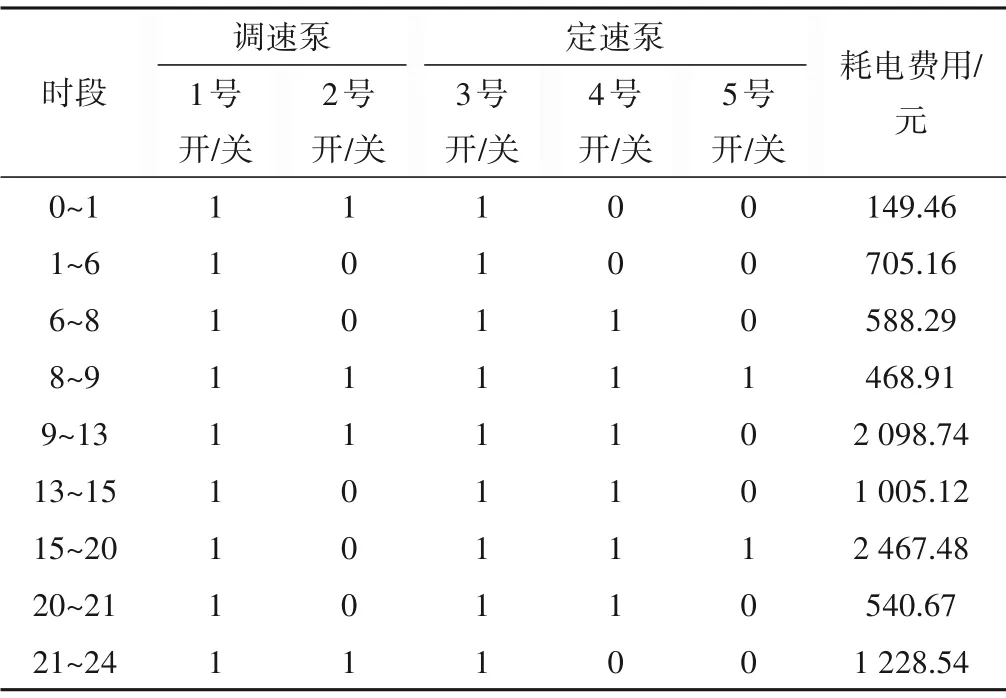
表4 各水泵启停状态Tab.4 The opening and closing status of each pump

3.2 泵站日运行优化

对于供水泵站，保证泵系统高效运行也应避免泵频繁启闭，对各泵进行损耗评估，按以下步骤求解日运行模型：

STEP 1：采用本文算法逐次对单一时段进行求解，得到单位时段初步运行方案。

STEP 2：根据时运行方案，并结合各泵启闭损耗，以全时段总电费与启停泵损耗之和为最优指标，采用动态规划方法求解，得到最终日运行方案。

3.2.1 时运行优化

以6～7时段为例，该时段流量需求Qe=3 230 m3/h，扬程需求He=42 m，初步运行方案如表5所示。

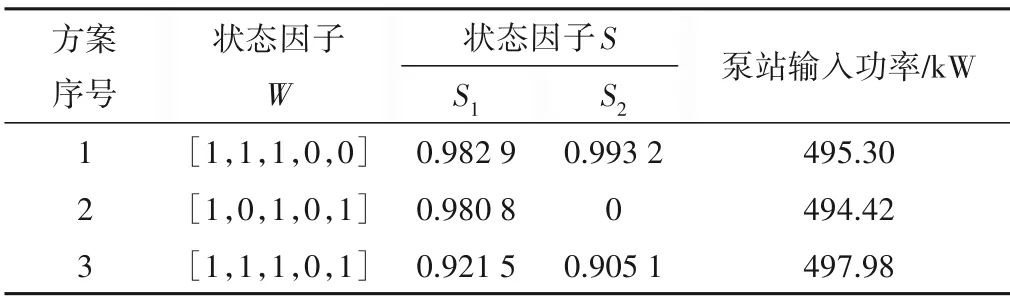
表5 6～7时段初步运行方案Tab.5 Simulation results of 6～7 h

从优化结果来看，虽然各方案组合不同，但泵站输入功率相差并不大，考虑水泵启停带来的损耗，对各泵进行启闭损耗评估，从泵额定流量、额定扬程、效率等方面综合评价，各泵启停损失如表6所示。

表6 泵启停损耗信息 元/台Tab.6 Loss information of pump opening and closing

3.2.2日运行优化

动态规划模型如下：

阶段变量t：t=1，2，…，n（n为时段数）。

状态变量θt：第t阶段的泵组调速比。

决策变量λt：第t阶段电费与该阶段初始状态至下一阶段初始状态因启停泵带来的损耗之和。

状态转移方程：

状态转移决策：由前一时段的任意状态向后一时段的任一状态的转移必须满足前一时段电费与前后状态的启停泵损失之和最小原则。

以最小花费（全时段总电费与启停泵损耗之和）为最优指标，构造逆序递推方程：

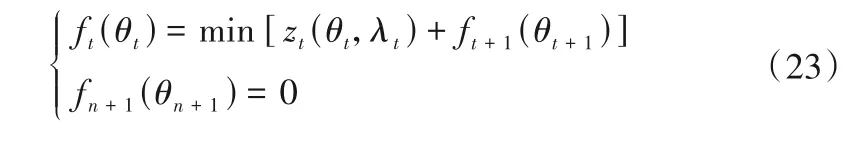
式中：zt(θt，λt)为第t至第t+1 阶段指标函数；ft(θt)为第t至第n阶段目标函数，最终日运行最佳运行结果如表7所示。

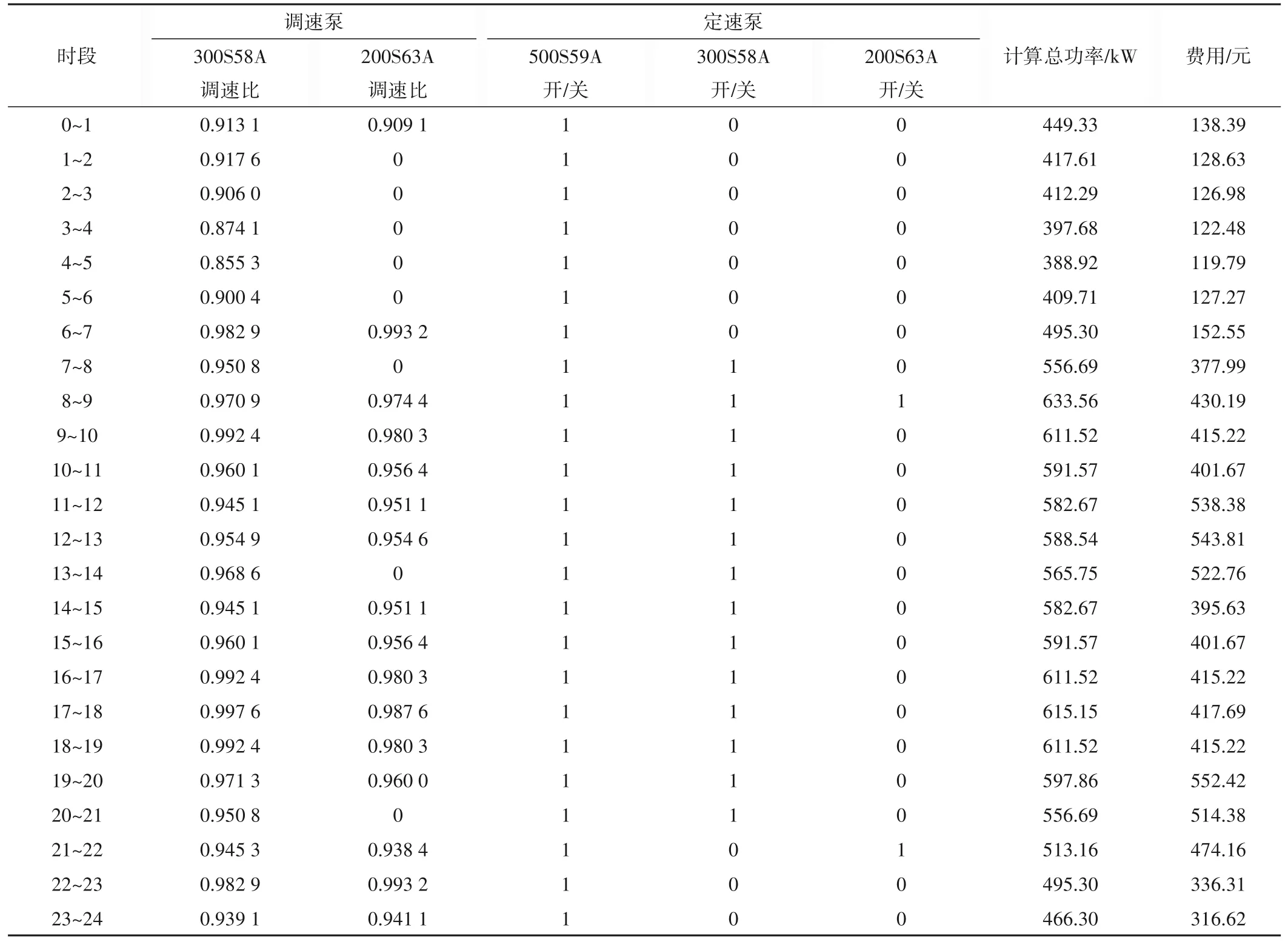
表7 泵站分时运行结果Tab.7 Timesharing operation scheduling results of pumping station

在考虑了分时电价与泵启停损耗等因素后，得出泵站日运行优化后的费用为8 385.43 元，且在改进方案中减少了泵启闭次数，改进方案节电率为：

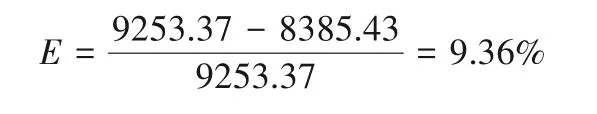
4 结 论

在供水泵站优化模型的基础上，对粒子群算法进行改进并将其应用于工程实例，研究结果改善了各泵运行工况，减小了泵站运行能耗。主要结论如下：

（1）考虑单泵高效区工况约束，变速泵调速比约束建立以泵站总输入功率最小为目标函数的运行优化模型可确保变速泵和定速泵运行在最优工况，避免大幅度偏离设计工况的情况，提升了泵送系统的运行效率和稳定性。

（2）对算法参数进行改进，使粒子根据迭代次数的变化有针对性的寻优方向。同时结合了模拟退火提升粒子跳出局部优解的能力，并加入柯西变异操作增加粒子多样性，提升了算法逼近最优解的能力。

（3）建立考虑了分时电价及泵启停损耗因素的运行优化模型更贴合实际，工程实例进一步表明改进后的粒子群算法对复杂模型具有良好的适应性，优化后的运行方案可使系统能耗降低9.36%，节能效果明显。