基于铣削系统动力学响应的球头铣刀铣削表面形貌建模

董永亨， 李淑娟， 张倩， 李鹏阳， 李旗， 贾祯， 李言

(1.西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048; 2.桂林电子科技大学 机电工程学院, 广西 桂林 541004)

0 引言

零件的表面形貌对结合部接触状态、表面磨损、润滑状态、摩擦、振动等均有很大影响，快速预测加工表面的形貌对零件表面质量的提高至关重要。球头铣刀因加工对象适应性强等优点而被广泛应用于航空航天、模具和汽车等行业中重要零件的加工中。然而，对于高精度表面，大部分采用球头铣刀铣削后再抛光的工艺路线，不但耗时耗力，而且影响零件表面质量的一致性。随着高速加工技术、多轴控制技术和精密制造技术不断进步和日趋完善，通过球头铣刀精细铣削达到或接近零件的最终表面质量要求已经成为可能。然而，球头铣刀的刀齿形状复杂，切削时刀齿和工件之间的接触点在不断地发生变化，铣削过程中的几何和物理因素对表面形貌形成的影响机理复杂。特别是在弱刚度铣削系统中，加工过程中由振动诱导的工艺系统动态位移对表面形貌的影响严重，直接决定着表面的使用效果。因此，探寻考虑工艺系统动态响应的球头铣刀铣削表面形貌的建模与仿真方法具有重要的意义。

目前，铣削表面形貌建模与仿真的常用方法主要是Z-MAP法和数值计算法。

Z-MAP法是将工件进行离散，转换成-网格节点，再根据切削加工中刀齿的位置求取相应每个网格节点对应的坐标，最后利用--矢量来表述已加工表面。Altintas等给出一种通用螺旋铣刀切削刃几何模型，为复杂刀齿形状铣刀加工表面形貌的建模奠定了基础；阎兵等基于该方法建立了球头铣刀的表面创成模型，具有良好的可扩展性；Quinsat等基于该方法分析了不同加工参数集合对零件表面五轴加工表面形貌的影响；Liu等基于该方法开发出一个球头铣刀铣削表面特征和粗糙度的综合仿真系统，在该系统里可以研究切削参数、刀具跳动、刀具磨损和刀轴倾斜对表面的影响；范思敏等预测了球头铣刀铣削球面的表面形貌，为一般曲面加工表面形貌的建模奠定了基础。传统Z-MAP法虽然可以综合考虑多种因素对表面形成的影响，但仿真精度和效率依赖于工件网格精度、刀齿离散精度和加工时间步长，当仿真精度要求高时，仿真效率就会降低，为此，一些研究者对传统Z-MAP法进行了改进。赵厚伟等将具有高计算效率的实体建模法引入Z-MAP法中仿真预测了球头铣刀加工表面形貌，但是，实体建模法中忽略进给方向残留面积的缺点必然会影响结果的准确性。一些研究者用离散平面近似刀齿扫掠面，以提高Z-MAP计算效率。王仁伟等和Antoniadis等基于三角面和四边面的刀齿微元扫掠面假设较高效地仿真了球头铣刀铣削表面形貌，然而，用离散平面近似刀具扫掠面时，存在一定的近似误差，并且采样时间间隔越大，近似误差越大。

数值计算法是在建立刀齿相对于工件的运动轨迹的基础上，通过数值迭代的方法求解方程组，求出工件某坐标平面上选定点对应的输入参数解，并将这些解回代方程组求出相应的轴向或法向高度，以最小的高度值作为坐标平面选定点高度，进而构建出整体加工表面形貌的一种建模方法。Gao等基于牛顿迭代法仿真了立铣刀周铣表面形貌，为球头铣刀铣削表面形貌仿真提供了思路；谭刚等和Zhang等提出一种球头铣刀多轴铣削表面形貌仿真的广义迭代算法，无需离散刀齿，也无需对工件划分网格，具有通用性好的特点；Chen等用牛顿- 辛普森公式求解了球头铣刀间歇进给方向表面凹坑的高度坐标，但对进给方向表面凹坑的忽略容易在高速加工中引起较大的误差；Mizugaki等提出一种球头铣刀等高加工球面表面形貌的预测方法，用牛顿- 辛普森法求解出球面上对应位置的法向高度，但需借助CAD系统绘制出表面形貌；Arizmendi等基于切比雪夫展开式转换提出了预测球头铣刀加工表面形貌的模型，虽然无需设置初始点，但超越方程组的求解难度较大。数值法可以看作是运动学求逆解的过程，该方法在计算精度和计算效率上，都摆脱了对离散精度的依赖。然而，数值计算法主要从运动学角度计算最终成形表面的高度坐标，较难将诸如振动诱导下刀具和工件的动态位移等因素直接考虑进去，同时，数值计算的精度和效率与迭代精度的设置和初始点的选择有很大关系。

文献[20-21]将Z-MAP法和数值计算法有机地结合起来完成了球头铣刀铣削表面形貌的建模与仿真，较好地兼顾了计算精度和效率，但未考虑工艺系统动力学响应的影响。梁鑫光等也综合应用这两种方法，提出考虑系统动态位移的球头铣刀铣削表面形貌的仿真方法，然而，在计算表面残留高度坐标时仅通过线性叠加的办法考虑振动位移所引起的高度坐标变换，而忽略了在振动作用下作用于工件网格点的刀齿位置点变化。

本文以弱刚度铣削系统中球头铣刀铣削表面形貌建模与仿真为研究对象，在建立刀具运动学模型和工艺系统动力学响应模型的基础上，综合应用Z-MAP法和泰勒公式，建立加工轨迹驱动下的球头铣刀铣削表面形貌的几何仿真模型，并记录工件网格点的刀齿作用点和作用时间等信息。在此基础上，以切削时间为纽带，根据工艺系统的动态位移使用泰勒公式和线性插值法修正工件网格点的相关信息，求出考虑工艺系统动态位移的工件网格点高度，进而获得考虑动力学相应的表面形貌。

1 刀齿几何运动轨迹方程的建立

为了清楚地表达球头铣刀铣削过程中刀齿上任意切削点的轨迹方程，建立如图1所示的坐标系。图1中：(简称{})为固连在工件上的全局坐标系；(简称{})为刀具瞬时进给坐标系，坐标轴矢量与进给速度方向平行且同向，为理想的被加工表面法线方向，指向实体外，为与的叉乘，也为和的叉乘；(简称{})为主轴随动坐标系，该坐标系固连在机床主轴上，与主轴轴线重合，且使刀具远离工件方向为正向，当与完全重合时，该坐标系的另外两个坐标轴及其方向与{}的完全重合，但是，实际工况中当刀具姿态调整时，与之间存在夹角，该情况是使{}通过相对于和的旋转实现主轴姿态的调整，进而实现刀具姿态的调整，从而获得不同的铣削方式；(简称{})为刀具坐标系，坐标原点固连在刀具的球头中心，与刀具的理论轴线重合，且与始终保持平行，二者之间的距离为，与基准刀齿(第1个刀齿)刃线在坐标平面上投影线起点的切线方向重合，该坐标系绕主轴坐标系中的坐标轴以角速度旋转，坐标轴与之间的夹角为+(为主轴未开始旋转的初始状态下二者之间的夹角，为时刻主轴旋转过的角度，=)；(简称{})为刀齿的局部坐标系，坐标原点也固连在刀具的球头中心，坐标轴与完全一致，坐标轴与刀齿的刃线在坐标平面上投影线起点的切线方向重合。

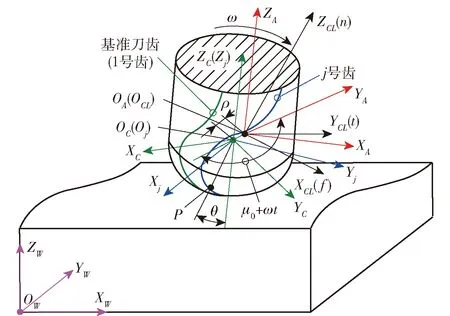
图1 球头铣刀铣削运动的参考坐标系Fig.1 Reference coordinate system for ball-end milling

图2 考虑刀具跳动的坐标系Fig.2 Coordinate system considering cutter’s jump

由于制造和装夹误差等因素的影响，刀具的中心轴线与主轴的中心轴线之间总存在偏心，如图2所示，为点的轴向位置角(°)。假定刀具中心和主轴中心之间的偏心距离为(mm)，矢量相对于坐标轴的夹角为(°)，且规定绕坐标轴顺时针旋转方向为正；主轴顺时针方向旋转，其转速为(r/min)，则角速度=π30(rad/s)，则(s)时刻旋转过的角度=180π(°)，{}相对于{}的变换矩阵为

(1)

式中：=+，为初始状态下与的初始夹角，顺时针旋转方向为正，为了简化研究，本文设定=0°。

球头铣刀铣削中往往使刀具相对于工件被加工表面倾斜，形成如图3所示的侧倾角(°)和前倾角(°)。先使{}绕旋转角度′(°)，使′=arctan (tancos)，再使{}绕旋转角度，且规定绕坐标轴矢量正向逆时针旋转方向为正，反之为负。则{}相对于{}的变换矩阵

(2)

本文以单向直线进给铣削平面为研究对象，如图3所示，此时

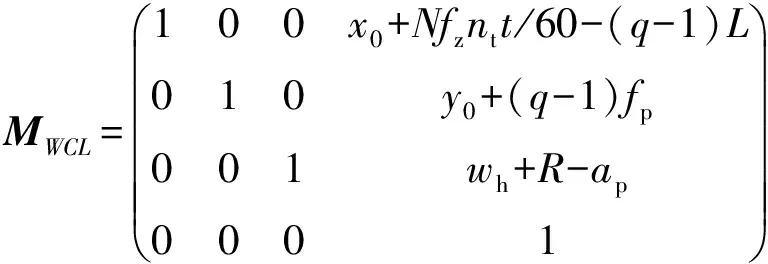
(3)

图3 刀具的姿态调整及走刀Fig.3 Gesture adjustment and feed of the cutter

式中：(,)为首次进给时在{}中的起始位置；为刀具进给次数，=1,2,3…；为每齿进给量(mm/r)；为进给行距(mm)；为单次走刀长度(mm)；为毛坯高度(mm)；为刀具半径(mm);为吃刀深度(mm)。

以定导程螺旋刃球头铣刀为切削刀具，通过齐次坐标矩阵变换可得到加工过程中刀齿上任意点在工件坐标系{}下的轨迹方程：

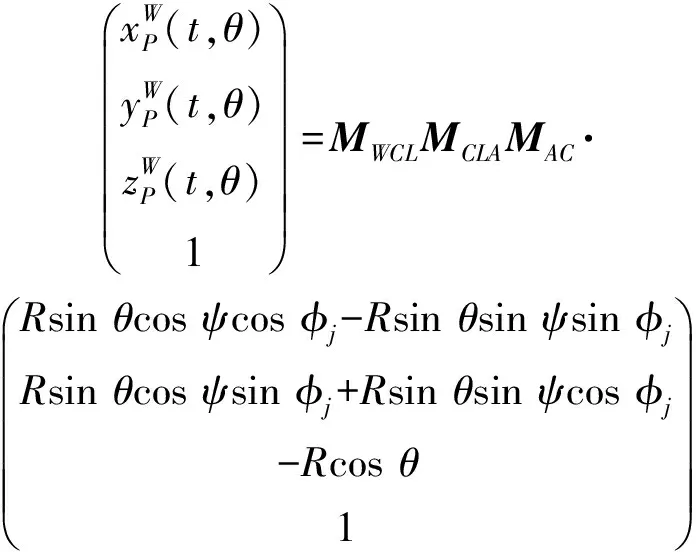
(4)

式中：为该点所对应的螺旋滞后角(°)，=180tan(1-cos)π，为圆柱面上刀齿刃口曲线的螺旋角(°)；为刀齿与基准刀齿的夹角，=360(-1)(°)，为刀齿总数，=1～。

2 铣削系统动力学响应的建模

在弱刚度铣削系统中，由于刚度、阻尼和惯性的作用，刀具和工件会在铣削力的激励下产生振动，进而诱导产生动态位移，该动态位移会叠加到刀齿几何运动轨迹上，从而对加工表面形貌产生直接影响。

2.1 瞬时铣削力的求解

按照切削力机械建模法的思想，首先需要对刀齿微元进行微元切削力的建模，为此，将刀齿分割成等刀齿轴向位置角增量的诸多刀齿微元，如图4所示，(,,)为与刀齿上离散点在时刻所在位置的连线在平面上的投影相对于坐标轴矢量顺时针转过的角度(°)，称为实际径向位置角。以刀齿离散点的特征信息来代表刀齿上(-1)～点之间的刀齿微元信息，刀齿上的微元在时刻所受的切削力可以分解为切向单元力切削力d(,,)、径向单元力切削力d(,,)和轴向单元力切削力d(,,)，结合切削力的机械建模法，考虑到球头铣刀刀齿的不同轴向位置角处切削状态的不同，综合考虑剪切和耕犁的共同作用，将其表示为

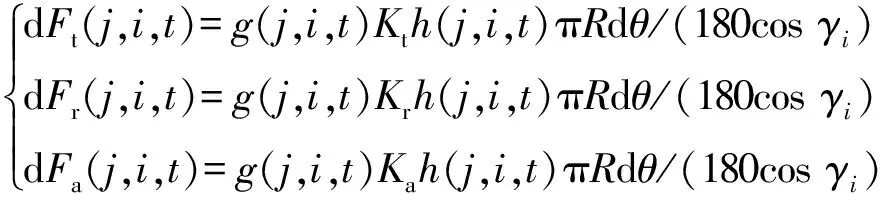
(5)

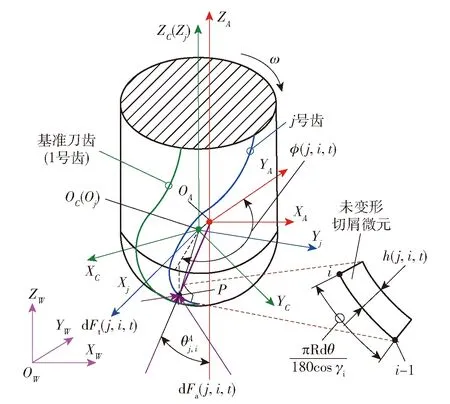
图4 刀齿微元受力图Fig.4 Force diagram of the discrete cutter teeth element

图5 刀- 工切触状态的识别Fig.5 Identification of the cutter-workpiece engagement state

图6 未变形切屑厚度求解示意图Fig.6 Schematic diagram of the solution for undeformed chip thickness

将刀齿微元瞬时所受的切向力、径向力和轴向力通过(6)式转化至主轴随动坐标系{}下，即

(6)

则刀具在时刻所受的瞬时切削力在主轴随动坐标系{}下可表示为

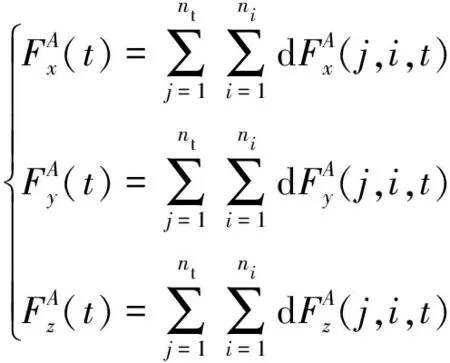
(7)

式中：为刀齿微元总数。

通过齐次坐标变换原理得，刀具在时刻所受的瞬时切削力在工件坐标系{}下可表示为

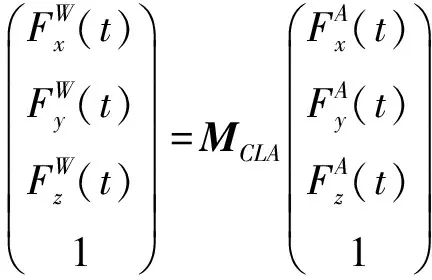
(8)

2.2 工艺系统动态位移的求解

弱刚度铣削系统中工件和刀具振动的激励包含静态铣削力，而且包含动态铣削力，该动态铣削力主要由切削过程的再生效应产生。如图7所示的弱刚度铣削系统，实际的切屑厚度不但包含名义厚度，还包含了振动诱导下刀具和工件的动态位移所引起的再生切屑厚度。

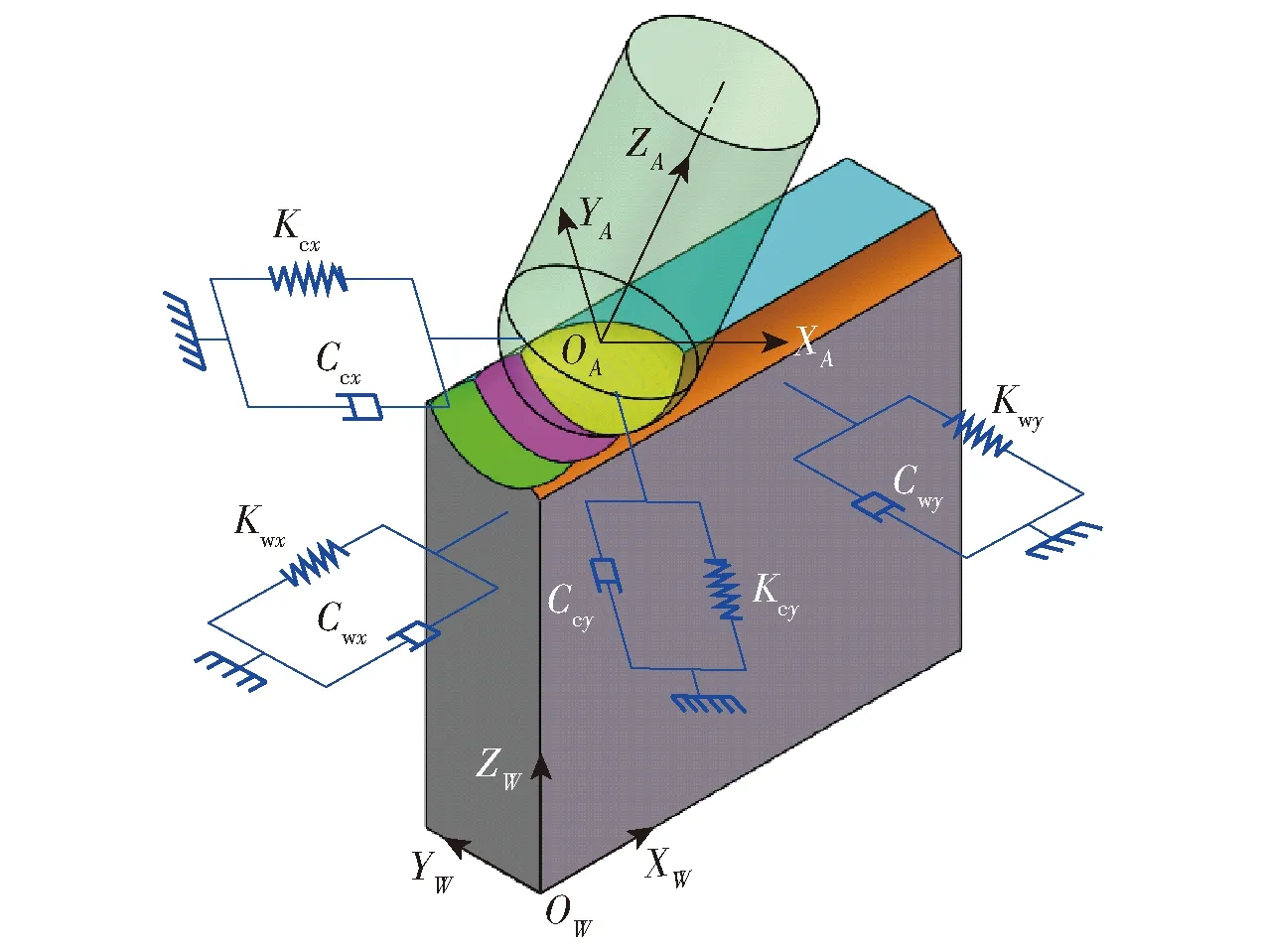
图7 柔性刀具- 柔性工件动力学铣削系统Fig.7 Dynamic milling system of flexiblecutter-flexible workpiece

在铣削过程中，可以将刀具和工件简化为如图7所示的两个垂直方向弹簧- 阻尼系统，则其动力学方程为

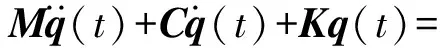
(9)

式中：、、分别为系统的模态质量矩阵、模态阻尼矩阵、模态刚度矩阵，

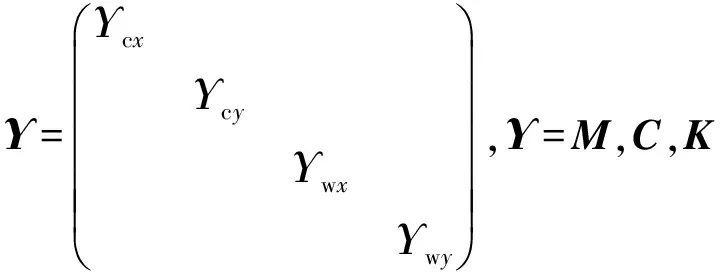
(10)

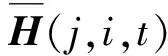
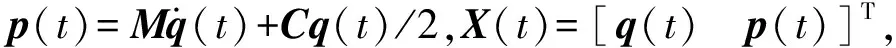
(11)

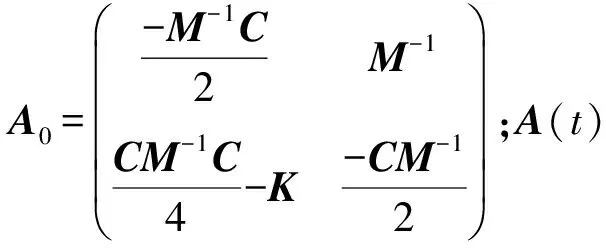
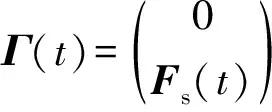
(12)

受刀齿结构和刀具跳动等因素的影响，球头铣刀在铣削过程中的时滞量随着刀齿、刀齿上的微元和切削时间的变化而变化，因此，稳定性分析中的时滞时间不再是刀齿的切削周期，而是主轴的旋转周期，=60。根据文献[26]，为了保证计算精度，在设定时间步长时需保证不能大于刀具- 工件系统最高振动模态周期的14倍，按照此要求将均匀地分为份，则时间步长单元

(13)

在Ding等提出的全离散法基础上考虑切削过程的变时滞特性，求解(11)式就可以获得球头铣刀切削系统中工件和刀具的动态位移()、()、()、()。

2.3 考虑刀具和工件动态位移的刀齿运动学建模

(14)

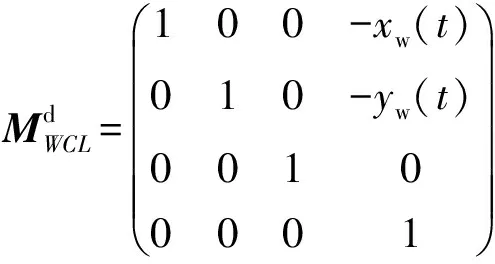
(15)

因此，综合考虑第1节所述的加工轨迹驱动下的刀具相对于工件的纯几何运动和振动诱导下刀具和工件的动态位移，则刀具坐标系{}相对于{}以及瞬时进给坐标系{}相对于{}的齐次变换矩阵分别如(16)式和(17)式所示：

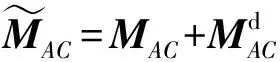
(16)

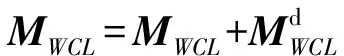
(17)

结合(4)式，可以得出在考虑刀具和工件的动态位移情况下球头铣刀加工过程中刀齿上任意点在工件坐标系{}下的轨迹方程：

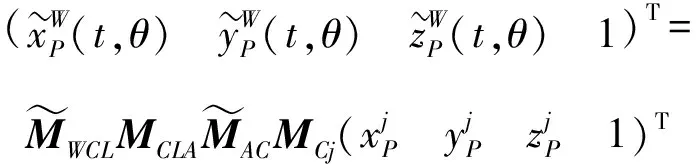
(18)

因此，振动诱导下刀具和工件的总动态位移在工件坐标系{}下可以表达为

(19)

由(4)式、(18)式和(19)式，可得

(20)

3 表面形貌的仿真

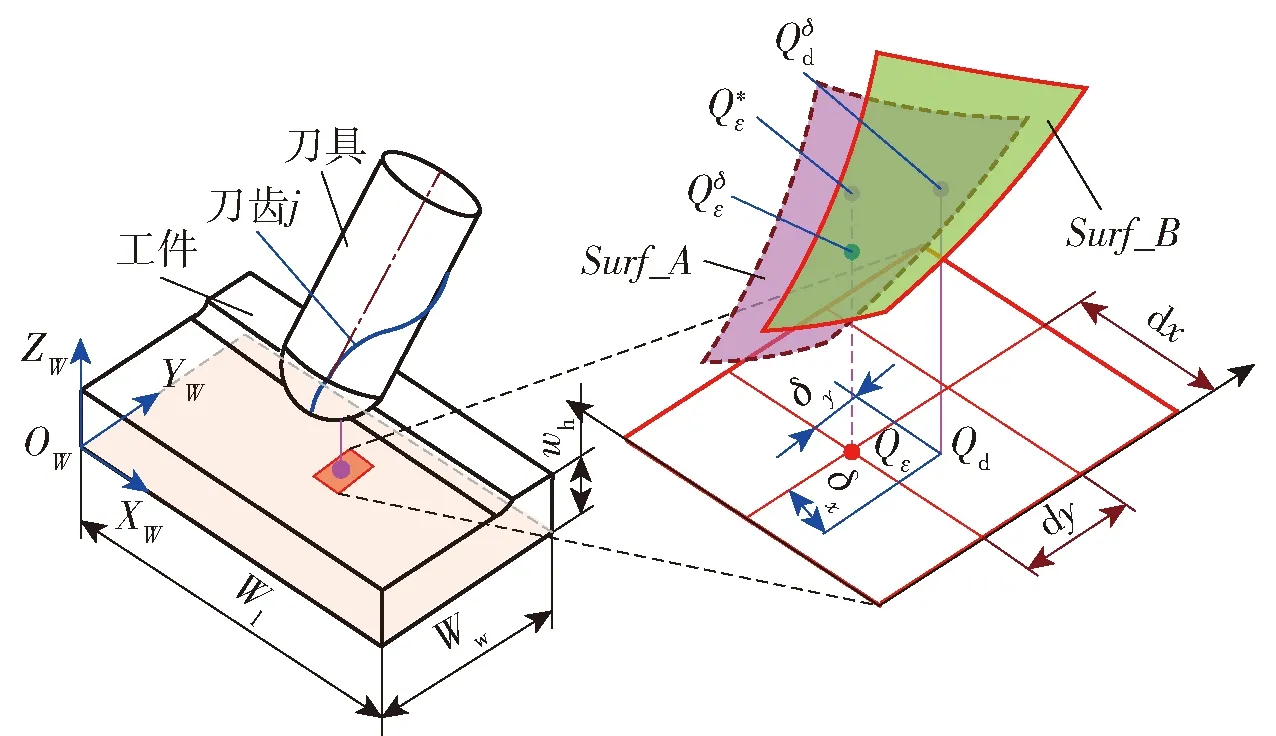
图8 考虑动力学响应的刀齿扫掠工件网格点高度求解示意图Fig.8 Schematic diagram for calculating grid point height of workpiece swept by cutter teeth considering dynamic response

考虑振动诱导下刀具和工件动态位移的球头铣刀铣削表面形貌的仿真过程如下：

1)参数设置。参数主要包括：

①毛坯尺寸及其Z-MAP模型表示，设置工件毛坯尺寸为××，用×个网格离散工件，保证图8所示的工件在轴和轴方向的网格间距d和d满足条件：max (d,d)≤15 min(,)；为了给工件的每个网格点赋予更多的信息，引入结构体数组[,](其中，=1，2，…，+1；=，2，…，+1)表示工件网格点的相关信息，同样，用结构体数组的元素[,]·表示工件网格点(,)的高度坐标，仿真初始，为每一个结构体数组元素(,)·赋值，网格点(,)的其它信息如表1所示。

表1 工件网格关联信息

②切削参数设置，主要有主轴转速、每齿进给量、吃刀深度和切削行距等。

③刀具参数设置，设置球头铣刀半径、刀齿总数和螺旋角等，离散刀齿，设置刀齿上相邻两离散点的轴向位置角增量=180min (d,d)(π)，以保证刀齿微元在平面的有投影长度不超过d或d。

④刀具姿态设置，主要有侧倾角和前倾角。

⑤表面形貌仿真时间步长的设置，为了保证计算精度，在离散切削时间时需要保证单位时间步长内刀齿离散点的扫掠轨迹曲线的弧长不大于工件网格间距，如(21)式所示：

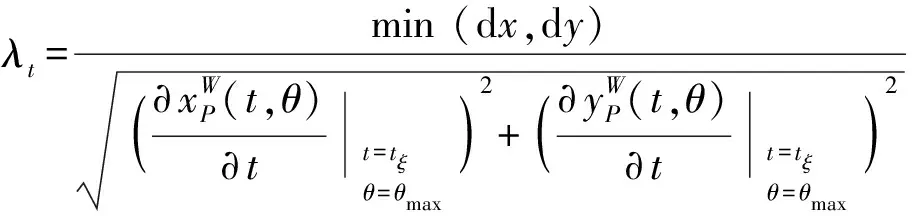
(21)

式中：为最大轴向位置角，=arccos((-))。

⑥按(13)式设置用于切削系统动态位移计算的时间单元。

2)静态铣削力计算。 在不考虑诱导产生铣削系统动态位移引起未变形切屑厚度变化的情况下，按照(5)式～(8)式计算球头铣刀铣削过程中的静态铣削力。

3)刀具和工件动态位移的计算。 按照22节求解在静态力和再生效应所引起的动态力的共同作用下刀具和工件的动态位移，并按(19)式获得工件坐标系{}下的任意切削时刻的总动态位移坐标((),(),())。

4)表面形貌的几何仿真。 基于(4)式所建立的加工轨迹驱动下的刀齿运动轨迹方程，根据Z-MAP思想完成球头铣刀铣削表面形貌的几何仿真，为了在保证精度的前提下提高仿真效率，表面形貌的几何仿真分两步完成：表面形貌的预备几何仿真和建立在其上的正式几何仿真。

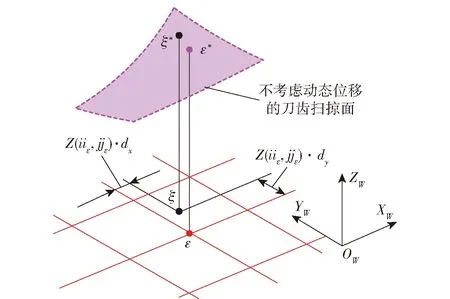
图9 球头铣刀铣削表面形貌几何仿真示意图Fig.9 Schematic diagram of geometric simulation of ball-end milling surface topography

(22)

上述用接近工件网格点的刀齿扫掠点高度坐标近似计算工件网格点高度坐标的方法虽然能够提高仿真效率，但是存在一定的近似误差，为此，在通过预备性几何仿真获得工件网格点相关的近似切削信息后，考虑到轴和轴方向坐标的近似误差不会超过各自方向网格间距的一半，因此，可以基于刀齿运动方程的泰勒展开式实现误差修正，进而获得准确的表面形貌几何仿真效果。由泰勒公式和(4)式，可得

(23)

解方程组可得Δ和Δ，结合(4)式和(23)式，工件网格点对应的当前时间段内刀齿扫掠面上的点的高度坐标为

(24)

用更新结构数组元素(,)·，并用(,)·+Δ和(,)·+Δ更新(,)·和(,)·，依次类推，按照此方法修正工件网格点的信息，通过各网格点修正后的(,)·值可以实现准确的表面形貌几何仿真。

5)考虑振动诱导下工件和刀具动态位移的表面形貌的物理仿真。通过几何仿真获取了工件各网格点由几何运动驱动的刀齿扫掠信息，但是，在振动诱导下刀具和工件动态位移的影响下，由几何仿真所得到的刀齿扫掠信息会发生变化，从而导致工件网格点的扫掠高度也发生改变，因此，在考虑该动态位移的表面形貌物理仿真中需要重新计算。由于在实际加工中振动诱导的刀具和工件动态位移较小，因此，在获取表面形貌的几何仿真结果及刀具和工件动态位移结果基础上，基于泰勒公式计算振动作用下加工表面的实际高度，进而获得表面形貌的物理仿真结果。首先，需要求取每个工件网格点所对应的刀具和工件动态位移坐标，由步骤4获取几何运动驱动下每个工件网格点(,)的刀齿作用时间(,)·，通过其与动态位移计算时间单元的比值(,)·可以获取该时间在动态位移时间历程中的位置，由于用于表面形貌仿真计算的时间步长与的尺度不同，因此，(,)·在动态位移时间历程中往往处于某一个区间，假定(,)·∈(,(+1))(=0,1,2,…)，而由(19)式可以获得在某时间点=,(+1)处刀具和工件的动态位移坐标((),(),())和((+),(+),(+))，则可以由(25)式插值求得(,)·所对应的动态位移坐标值

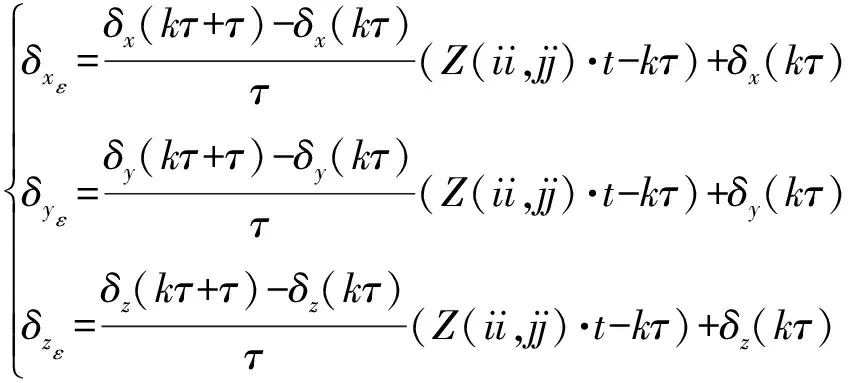
(25)

由泰勒公式和(20)式，可得

(26)

按照(20)式将(26)式展开，可得

(27)

解方程组可得Δ和Δ，由此可得，在振动诱导的刀具和工件动态位移作用下，工件网格点(,)的刀具作用时间和作用刀齿的轴向位置角分别如(28)式和(29)式所示：

(,)·=(,)·+Δ

(28)

(,)·=(,)·+Δ

(29)

设=⎣(,)·」+1，则在振动诱导的刀具和工件动态位移作用下，工件网格点(,)的高度坐标更新为

(30)

4 实验验证

采用秦川机床厂生产的加工中心MV510作为实验机床，该机床的最高主轴转速为5 000 r/min，定位精度为0.018 mm，重复定位精度为0.008 mm；实验刀具是整体长度为120 mm的Y330整体式硬质合金螺旋刃球头铣刀，其直径为10 mm，齿数为2，螺旋角为35°，弹性模量为210 GPa，刀具的装夹悬伸长度为85 mm，安装之后经测得径向跳动量为0.028 mm；工件材料为航空铝合金7050-T6，工件的长×宽×高为42 mm×11 mm×180 mm；为了在三轴机床上使刀具相对于工件的姿态调整，采用组合夹具的基础板和圆柱支撑部件，按照正弦规的工作原理调整角度。

铣削系统的动态性能测试系统由力锤、加速度传感器以及对应的数据采集设备和信号分析软件LMS Test. Lab8B组成，如图10所示，测试中采用力锤激励，假定切削力集中在刀头处，在刀头上安装加速度计，测量刀头处的响应加速度，数据采集器将力锤激励信号和加速度信号数字化采集到计算机上，然后由信号分析软件LMS Test. Lab8B进行分析和处理，得到系统动态性能参数，结果如表2所示。

图10 弱刚度铣削系统动态性能参数测试及切削实验Fig.10 Dynamic property test and milling experiments for the weak-stiffness milling system

表2 刀具和工件的模态参数

在表3所示的切削条件下进行加工实验，加工结束后用酒精擦拭加工表面，接着用德国产的徕卡激光共聚焦显微镜DCM-3D测量表面形貌，该设备的分辨率为0.1 nm，如图11所示。

表3 实验的切削参数

图11 表面形貌测量装置Fig.11 Surface topography measuring device

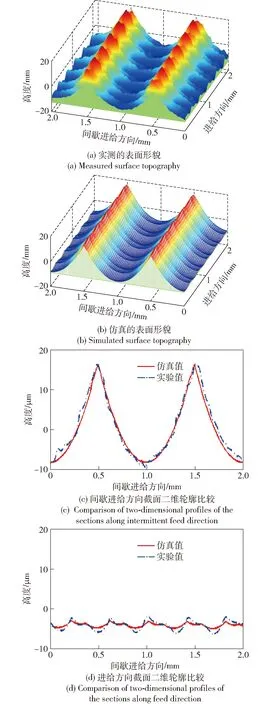
图12 弱刚度铣削系统加工表面形貌的仿真和实验结果对比Fig.12 Comparison of simulation and experimental results of surface topography machined by a weak-stiffness milling system

球头铣刀铣削表面形貌的实测和仿真结果如图12所示，二者的表征参数表面幅度算术平均偏差及轮廓幅度算术平均偏差对比如表4所示，无论从整体形状，还是的对比结果上可以看出，仿真与实测结果都比较接近，二者在间歇进给方向的相应截面轮廓的吻合度也很高，主要是因为该方向截面轮廓是刀齿廓形的“复印”，实验所用刀具的刀齿锋利，且主轴转速高，加工过程中不易产生积屑瘤，金属在该方向的塑性流动小。然而，进给方向上的截面轮廓虽然在变化趋势上一致，但有一定的差异，主要有以下5方面原因：

1)在强迫振动的冲击作用下，弱刚度刀具的中心轴线较大幅地偏离主轴中心轴线，可能会出现副后角切削的情况，此时，刀齿后刀面与工件的摩擦增大，会使残留凸体顶部的金属略微向图示右边偏坍，使得峰谷截面曲线出现了图示的偏态分布特点；

2)在冲击力和摩擦力的共同作用下，接近刀齿刃带的金属会发生较大的塑性流动，流动方向沿着进给方向，接近塑性流动层的金属会发生塑性变形和弹性变形，当刀齿切离工件时，又有弹性变形的恢复，从而使得实测轮廓的波动与理论仿真的有一定差异；

3)刀齿在工件表面形貌的谷底换向切出时可能会使金属从基体撕裂，从而导致轮廓谷深较大；

4)由于更强的摩擦和挤压作用，使得轮廓峰顶略向左偏移，造成了毛刺翻边，使得粗糙度值增大；

5)力锤敲击法测量模态参数存在一定误差，会对工艺系统动态位移的计算精度产生一定的影响，进而对表面形貌预测产生直接影响。

表4 弱刚度铣削系统中实测和仿真表面Sa的对比

若改用文献[21]所提出的方法实现本例的表面形貌几何仿真环节，最终仿真所获得表面形貌的为6.49 μm，在精度上与本文所提方法相当，而仿真计算所需的时间为695.4 s，相对于本文方法(551.2 s)效率显低。

从整体上来讲，仿真结果与实测结果有较好的一致性，可以用于弱刚度球头铣刀铣削表面形貌的预测之中。

5 结论

1)按照齐次坐标变换原理建立了加工轨迹驱动下的球头铣刀刀齿的运动方程，综合Z-MAP法和泰勒公式，能够实现球头铣刀铣削表面形貌的预备性几何仿真和正式性几何仿真。

2)提出了考虑变时滞效应的弱刚度工艺系统动态位移的全离散求解方法，在修正刀具运动轨迹的基础上，通过改进Z-MAP法完成考虑振动诱导下工件和刀具动态位移的表面形貌物理建模，实现了弱刚度球头铣刀铣削系统铣削表面形貌的仿真。

3)在相同条件下，实验和仿真表面形貌的表面幅度算术平均偏差的绝对误差仅为0.02 μm，表明本文所所提出的考虑系统动力学响应的球头铣刀铣削表面形貌建模方法是可靠的，可以为实际加工中参数的选择和优化提供理论依据。