基于姿态反馈实现过载跟踪的飞行器控制方法
姜丽敏, 刘海亮, 陈曙暄
(北京航天自动控制研究所, 北京 100854)
0 引言
机动能力是衡量飞行器高性能的重要指标,而飞行器的机动能力则取决于飞行器对大过载的跟踪能力[1]。过载控制,即将过载直接作为状态量进行控制,能够直接对飞行器质心进行控制,故采用过载自动驾驶仪的飞行器控制系统制导时间短、脱靶量小,因此,为提高飞行器的机动能力,通常采用过载控制。
然而,飞行器在大空域机动飞行时,为提高射程,通常采用高低空混合弹道,当飞行器处于大攻角飞行状态时,气动参数相差悬殊(高达5~8倍),且通道间的本体耦合严重[2-7],使得基于过载反馈的自动驾驶仪无法提供满意的动态性能,甚至有可能使飞行器的稳定性发生变化[8],从而无法完成控制任务;而且,飞行器在宽速域宽空域飞行时,基于过载反馈的自动驾驶仪控制系统设计较为困难[9];此外,低速飞行状态下,气动参数偏差、大气模型偏差、风干扰等又对攻角/侧滑角指令有显著影响,导致难以实现对质心的精确控制[10]。因此,在兼顾飞行器机动能力需求的情况下,鲁棒性在飞行器控制系统设计中显得尤为重要。
为解决该问题,本文针对依靠空气动力提供控制力和控制力矩的飞行器,在构建俯仰- 偏航通道非线性数学模型的基础上,提出一种兼顾机动能力和姿态稳定性能的飞行器控制系统设计方法。该方法基于过载与飞行器姿态的等效转换,将制导律计算得到的过载指令转化为飞行器姿态指令,进而通过以姿态反馈为主、过载补偿为辅的控制系统设计达到对过载指令精确跟踪的目的。本文通过频域相对稳定性分析验证了该方法的稳定性;通过6自由度仿真验证了该方法在各项随机误差下既能满足制导对过载的跟踪精度要求,又能对飞行器进行姿态鲁棒稳定控制。该方法简单可靠,已得到工程应用验证。
1 数学模型
1.1 坐标系定义及转换
本节对本文方法使用的坐标系进行定义,并对坐标系之间的坐标转换关系进行建模。
机体坐标系(Oxbybzb):坐标原点为飞行器的质心O,Oxb轴沿飞行器纵轴指向飞行器头部;Oyb轴在飞行器纵向对称面内与Oxb轴垂直,向上为正;Ozb轴由右手定则确定。
速度坐标系(Oxvyvzv):坐标原点为飞行器的质心O,Oxv轴沿速度方向,与速度方向一致;Oyv轴在飞行器纵向对称面内与Oxv轴垂直,向上为正;Ozv轴由右手定则确定。
航迹坐标系(Oxtytzt):坐标原点为飞行器的质心O,Oxt轴沿航迹速度方向;Oyt在包含Oxt轴的当地铅垂平面内,垂直于Oxt指向上为正;Ozt轴垂直于Oxt,Oyt所在平面,符合右手准则。
发射惯性坐标系(Oxyz):坐标原点为发射瞬间的飞行器质心O,Oy与当地重力方向相反;Ox轴与Oy轴垂直,指向目标点;Oz轴由右手定则确定。该坐标系不随地球转动。
上述4个坐标系之间的关系网如图1所示。

图1 4个坐标系之间的关系网Fig.1 Relationship of the four coordinate systems
图1中:θt、σt、γvt分别为航迹倾角、航迹偏航角和倾侧角;φ、ψ、γ分别为飞行器的俯仰角、偏航角和滚转角;rx、ry、rz为飞行器当前点的地心矢径在发射惯性坐标系下的分量;vtdx、vtdy、vtdz为飞行器相对速度在发射惯性坐标系下的分量。

(1)
(2)
由航迹坐标系的定义,根据飞行器当前点在发射惯性坐标系下的地心矢径Rxyz=(rx,ry,rz)和飞行器相对速度在发射惯性坐标系下的矢量vtd=(vtdx,vtdy,vtdz),可得到发射惯性坐标系到航迹坐标系的坐标转换矩阵为
(3)
式中:
1.2 飞行器运动模型
本文以高超声速飞行器为研究对象,基于牛顿第二定律和动量矩定理,假定惯性积Jxy=0、Jyz=0、Jzx=0,可得到全通道运动模型为
(4)
(5)
式中:m为飞行器质量;v为飞行速度;θ为弹道倾角;σ为弹道偏角;Fvx、Fvy、Fvz为飞行器所受合力在速度坐标系下的3分量;Mx1、My1、Mz1为作用力对飞行器质心主矩在机体坐标系下的3分量;ωx1、ωy1、ωz1为飞行器绕机体3个坐标系的转动角速度;Jx1、Jy1、Jz1为飞行器各轴的主转动惯量。
作用在飞行器上的力有:1)作用在质心的地球引力;2)作用在气动中心上的空气动力;3)作用于推力作用点的推力;4)控制装置提供的控制力。将这些力分解到速度坐标系下,并进行线性叠加得到飞行器所受合力在速度坐标系的3分量为
(6)
式中:Px1为发动机推力在飞行器纵轴上的分量;α为飞行攻角;β为侧滑角;g为重力加速度;cx、cy、cz为速度坐标系下的气动力系数;q为动压;S为气动参考面积;Fcvx、Fcvy、Fcvz为控制力在速度坐标系下的三分量;Fdvx、Fdvy、Fdvz分别为其他干扰力在速度坐标系下的3分量。
相应地,作用在飞行器上的力矩包括空气动力矩、推力矩和控制力矩等。将这些力矩投影到机体坐标系下并进行线性叠加,得
(7)

联立(4)式、(5)式、(6)式、(7)式即可得到飞行器运动模型。
1.3 非线性过载模型
由过载的定义知,机体坐标系下飞行器质心的两个法向过载分别为
(8)
式中:Ftqby、Ftqbz为推力和气动力在机体坐标系下的分量;Fcby、Fcbz为控制力在机体坐标系下的分量;Fdby、Fdbz为其他干扰力在机体坐标系下的分量。

(9)
将(9)式代入(8)式,可见,(8)式是非线性的,且与攻角、侧滑角、姿态、重力等多种因素有关。对于某些外形的飞行器而言,如升力体类滑翔飞行器,当飞行高度和飞行速度确定时,由空气舵面偏转产生的气动力数值较小,此时可忽略(8)式中的Fcby、Fcbz,即此时的过载大小主要取决于攻角、侧滑角的大小。这就意味者,对此类飞行器而言,采用过载自动驾驶仪时,难以得到与过载指令精确匹配的舵偏角指令。
2 控制系统设计
从控制系统角度而言,飞行器有两个基本控制回路,即自动驾驶仪回路(也称“内回路”)和制导外回路。采用高低空混合弹道的飞行器,在大空域宽速域机动飞行时,其动力学特性会随飞行高度、飞行速度、大气密度、质心和压心等发生剧烈变化。因此,为保证制导精度,需要引入自动驾驶仪回路来改善动态特性,使其具有较好的稳定性和操纵性。
2.1 过载指令转化为姿态指令
自动驾驶仪回路有两种常用结构,分别为过载自动驾驶仪和姿态自动驾驶仪。
过载自动驾驶仪的输入为过载制导指令,姿态自动驾驶仪的输入为姿态制导指令。飞行器控制系统设计时,为增大战斗部的毁伤效果,地地、空地飞行器需采用大落角对目标进行攻击。为克服传统比例导引只能保证终端落点而无法实现大落角的问题,工程应用中纵向通道常采用的制导律[11-12]为
(10)
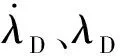
由(10)式得到发射惯性系下的过载制导指令:
nycx=aycx/g
(11)
为方便推导,忽略过载指令中的重力补充项。
那么,当制导指令为过载、内回路采用姿态驾驶仪时,如何将过载指令转化为姿态驾驶仪所需要的姿态指令,同时还能保证制导精度,值得研究。
(12)
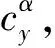
(13)

然后,基于过载与攻角的等效转换(参见1.3节),可将(12)式的过载制导指令,转化为攻角指令:
αcx=kαn·nybcx
(14)
同理,可由侧向过载指令得到侧滑角指令βcx,此处不再赘述。
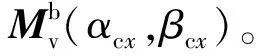
(15)
由(15)式,得到姿态角指令:
(16)
2.2 控制系统设计
2.2.1 控制系统结构
飞行器控制系统设计的目的是在飞行包线内跟踪指令的同时具有足够的稳定裕度来抵抗参数大范围变化的影响[13-15]。

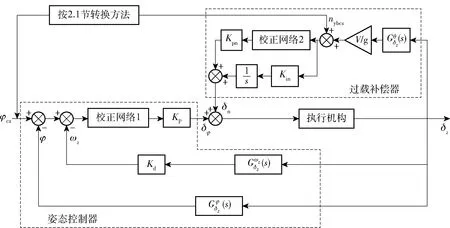
图2 控制系统结构图Fig.2 Structure diagram of the control system
图2所示控制系统的控制指令为
δz=WSF(s)(δφ+δn)
(17)
式中:WSF(s)为图2中执行机构的传递函数;δφ为图2中姿态控制器生成的控制指令;δn为图2中过载补偿器生成的控制指令。
图2控制器与经典三回路过载自动驾驶仪[16-17]相比,二者的共同点为都使用了过载指令、过载、飞行姿态角和姿态角速度,不同点为后者的姿态角速度反馈项是为了增大系统的阻尼。姿态角反馈项实际上是一个近似攻角的反馈信息,形成了与攻角近似呈比例的恢复力矩起到增稳作用,它本质上是以过载反馈为主回路的过载自动驾驶仪,因此无需将指令过载转换为姿态指令;而本文是采用2.1节方法将过载指令转化为姿态角指令,以姿态角信号为主反馈,达到对飞行姿态进行直接控制的目的,本质上是一个以姿态角反馈为主回路的姿态自动驾驶仪。图2中过载补偿回路的目的是提高低速飞行时的过载跟踪精度,而不是提高控制器的稳定性。
2.2.2 姿态控制器设计
图2中姿态控制器的目的是跟踪程序姿态角,采用姿态角偏差+姿态角速度的控制策略,控制方程为
δφ=KpW1(s)((φcx-φ)+Kdωz)
(18)
式中:W1(s)为图2中校正网络1的传递函数。
此外根据飞行器特性,可对(18)式的控制方程进行重新设计,并对图2所示控制系统中的姿态控制器框图进行相应的更改。
2.2.3 过载补偿器设计
图2中过载补偿器的目的是提高控制系统对过载指令的跟踪性能,采用过载偏差+过载偏差积分的控制策略,控制方程为
(19)
式中:W2(s)为图2中校正网络2的传递函数;nyb为当前飞行状态下飞行器的实际过载。
将(18)式和(19)式代入(17)式,得到图2所示控制系统的控制指令δz。
2.3 控制参数设计准则
由2.2节可知,图2所示控制系统具有2个校正网络和4个控制参数,即姿态控制部分的校正网络W1(s)、动态增益Kd、静态增益Kp和过载补偿器的校正网络W2(s)、比例系数Kpn、积分系数Kin。
校正网络和控制参数设计时,首先,沿飞行弹道,选取静不稳定度最大、调整比最大、动压最大和最小等典型特征时刻作为设计的依据;考虑到飞行过程中飞行环境、结构干扰等因素的影响,飞行器的飞行弹道会偏离标称弹道,因此,除沿标称飞行弹道选取典型特征点外,还需考虑偏差飞行弹道,使得设计的校正网络和控制参数确保飞行控制系统在干扰情况下也能实现稳定控制和跟踪。然后,根据频域相对稳定性指标要求(工程上,考虑各种偏差飞行弹道时,通常要求幅值裕度不小于2 dB,相位裕度不小于15°),确定校正网络和控制参数。同时,为解决飞行空域速域大范围变化下控制系统稳定性的自适应性,校正网络和控制参数根据飞行马赫数、动压、弹目距离等进行动态调整。
在上述准则下,采用回路整形法对(18)式和(19)式中校正网络进行设计。具体而言,首先绘制出被控对象的对数幅频特性曲线图;其次,根据期望的频域相对稳定性指标要求,在对数幅频特性图上用图解法初步绘制出校正网络的频域特性形状,它通常是多个1阶、2阶校正环节的串联;然后,基于对各种校正环节如滞后网络、超前网路、滞后- 超前网路及它们组合特性的理解,根据绘制的校正网络形状,利用常规的工程试凑方法可初步估计出校正网络的形式和参数,估计出的校正网络通常是多阶的;最后,将初步估计出的校正网络和未校正系统的开环频率特性相叠加,判断被校正后的系统是否稳定且具有要求的频域相对稳定裕度,不满足要求时修正幅频校正特性。由于设计的校正网络既要保证被校正后系统在各种飞行状态下均能满足频域相对稳定裕度要求,又能以简单的结构形式实现,因此需要反复地修改或调整校正网络的参数。显然,这是一个反复迭代优化设计,因此,校正网络参数的计算机辅助优化设计方法得到广泛研究。考虑到校正网络参数的自动寻优方法非本文重点,此处不做讨论,感兴趣的读者可查阅相关文献[18-20]。
2.4 频域稳定性分析
控制回路的开环传递函数是控制系统频域稳定性分析的基础。
记过载补偿内回路的反馈传递函数为G1(s) ,过载补偿内回路的闭环传递函数为Ggz(s)。根据图2可推导得到G1(s)和Ggz(s):
(20)

引入过载补偿回路,认为过载指令为慢变量。由此可得,图2中以Δφ为输入、φ为输出的开环传递函数G(s)为
(21)
式中:Gpd(s)为姿态角速度构成的内回路的闭环传递函数,
(22)
从标称飞行弹道和两条极限偏差飞行弹道3条弹道中分别选取最高点、静不稳定度最大、动压最大3个典型飞行状态(共计9个特征点),根据频域指标要求,进行校正网络和控制参数整定。
图3为飞行器本体的bode图,图4为9个特征点经控制器校正后的bode图。由图3可见,特征点1至特征点6均不稳定,特征点7的稳定裕度较小,特征点8不稳定,特征点9是相位不稳定的;由图4可见,经本文方法校正后,9个特征点均稳定。

图3 飞行器本体Bode图Fig.3 Bode diagram for the nine characteristic moments

图4 经控制器校正后的Bode图Fig.4 Bode diagram of the nine moments after beingcorrected by the controller
表1为9个特征点经控制器校正前后的稳定裕度。由表1中数据可知,除特征点7外,其他8个特征点的本体均不稳定;经本文控制器校正后,9个特征点均是稳定的,最小幅值裕度为2.63 dB,最小相位裕度为17.61°,满足频域相对稳定裕度指标要求。结果表明,通过设计控制器的校正网络和控制参数,本文方法能够对飞行器进行稳定控制。
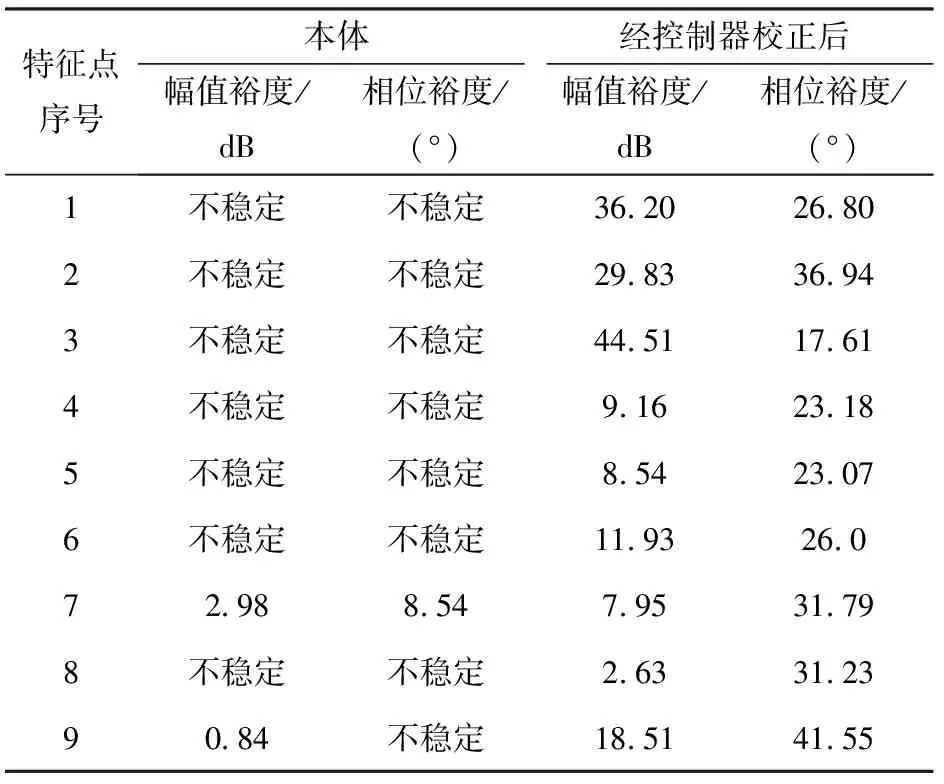
表1 9个特征点经本文方法校正前后的稳定裕度
3 仿真结果
为检验基于本文方法设计的飞行器控制系统的控制精度和鲁棒性,分别在气动参数标称、正向和负向拉偏,飞行器质心位置零偏差、正向和负向拉偏,大气模型参数标称、正向和负向拉偏多种偏差类型随机组合下进行6自由度仿真。
仿真初始条件为:飞行高度22 km、飞行速度马赫数Ma=5.0、初始攻角为11°、初始侧滑角为-1.1°。
图5~图11为标称模型下的飞行弹道仿真曲线。图12~图18为模型具有不确定性的飞行弹道仿真曲线,其中气动力系数cx、cy、cz在标称值cx0、cy0、cz0的基础上叠加10%的不确定度,即cx=(1+10%)cx0、cy=(1+10%)cy0、cz=(1+10%)cz0;气动力矩系数mx1、my1、mz1在标称值mx10、my10、mz10的基础上叠加25%的不确定度,即mx1=(1+25%)·mx10、my1=(1+25%)my10、mz1=(1+25%)my10;质心位置负向拉偏1%;大气密度正向拉偏10%。

图5 标称模型下飞行器俯仰角响应曲线Fig.5 Response curve of the pitch angle of the nominal model
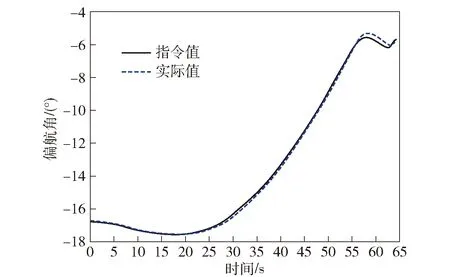
图6 标称模型下飞行器偏航角响应曲线Fig.6 Response curve of the yaw angle

图7 标称模型下飞行器滚转角响应曲线Fig.7 Response curve of the roll angle of thenominal model
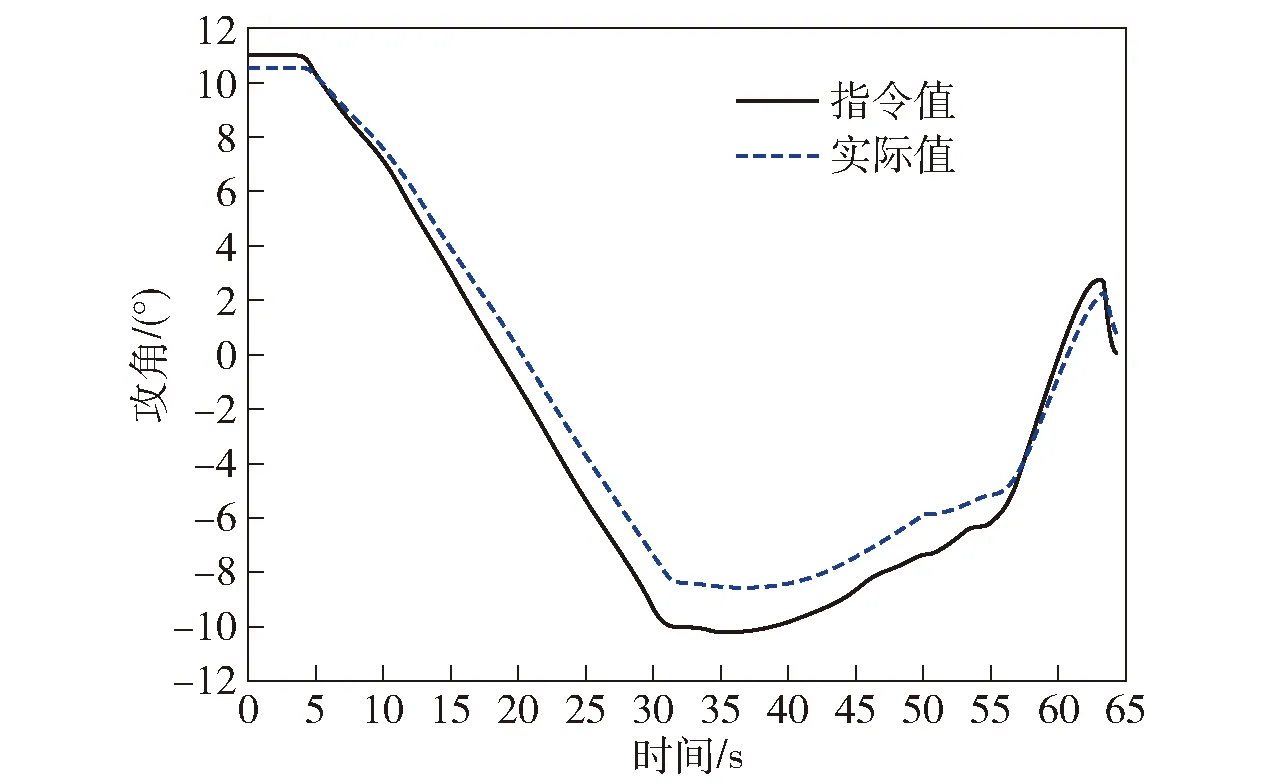
图8 标称模型下飞行器攻角响应曲线Fig.8 Response curve of the angle of attack of the nominal model
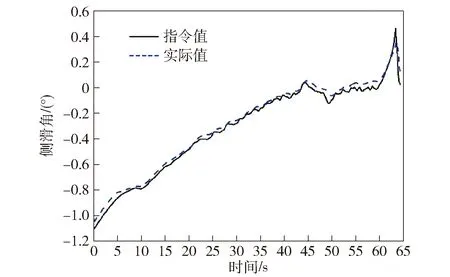
图9 标称模型下飞行器侧滑角响应曲线Fig.9 Response curve of the sideslip angle of the nominal model

图10 标称模型下飞行器y轴方向过载响应曲线Fig.10 y-axis overload response curve of the nominal model

图11 标称模型下飞行器z轴方向过载响应曲线Fig.11 z-axis overload response curve of the thenominal model
图5~图11的仿真结果说明:标称状态下,飞行器姿态角响应和过载响应均具有理想的动态特性与稳态精度。其中,俯仰角的跟踪误差在1.42°以内,最大值位于30 s附近;偏航角的跟踪误差在0.34°以内,滚动角的跟踪误差在0.49°以内,位于俯仰角跟踪误差最大的时刻。
图12~图18的仿真结果说明:模型存在不确定性时,飞行器姿态角响应和过载响应同样具有理想的动态特性与稳态精度。其中,俯仰角的跟踪误差在2.25°以内,最大值位于21.5 s附近;偏航角的跟踪误差在1.25°以内,滚动角的跟踪误差在0.91°以内,位于俯仰角跟踪误差最大的时刻。

图12 模型存在不确定性时飞行器俯仰角响应曲线Fig.12 Response curve of the pitch angle of the model under uncertainties

图13 模型存在不确定性时飞行器偏航角响应曲线Fig.13 Response curve of the yaw angle of the model under uncertainties

图14 模型存在不确定性时飞行器滚转角响应曲线Fig.14 Response curve of the roll angle of the model under uncertainties

图15 模型存在不确定性时飞行器攻角响应曲线Fig.15 Response curve of the angle of attack of the model under uncertainties
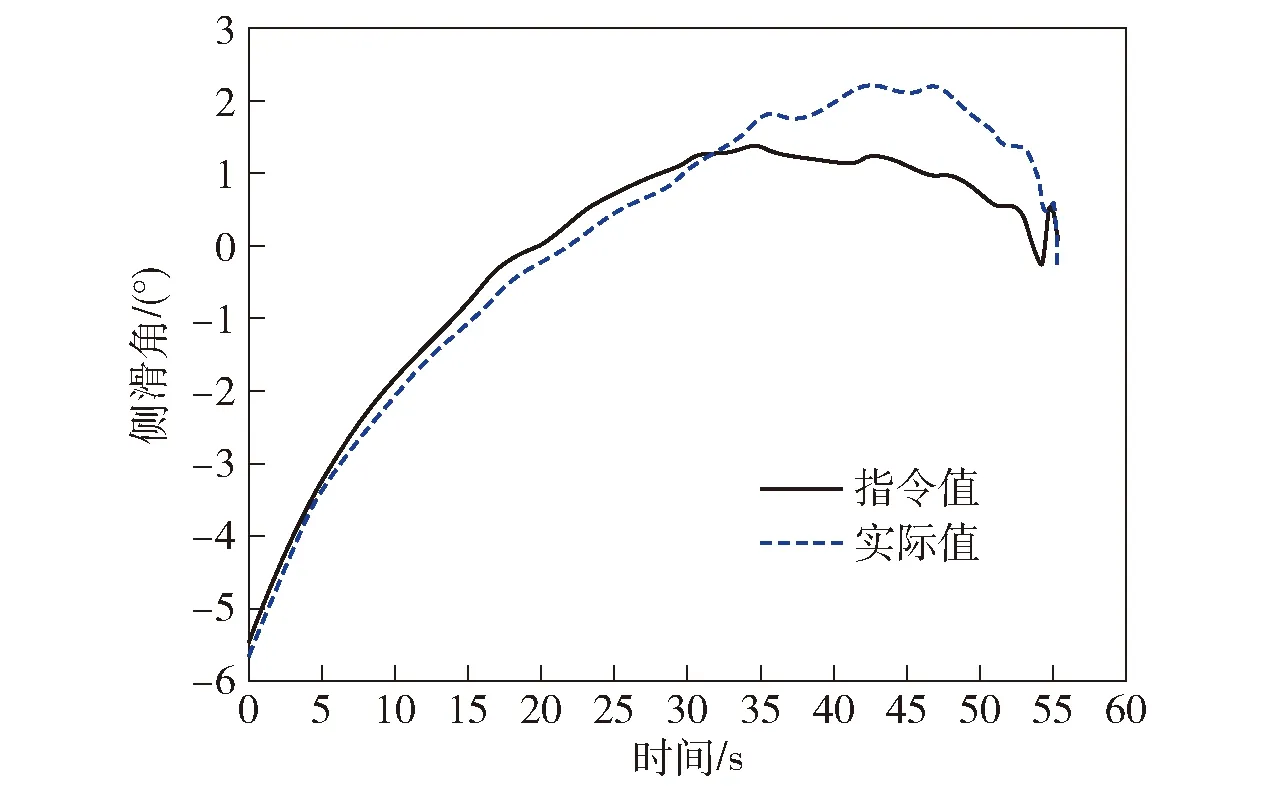
图16 模型存在不确定性时飞行器侧滑角响应曲线Fig.16 Response curve of the sideslip angle of the model under uncertainties

图17 模型存在不确定性时飞行器y轴方向过载响应曲线Fig.17 y-axis overload response curve of the model under uncertainties
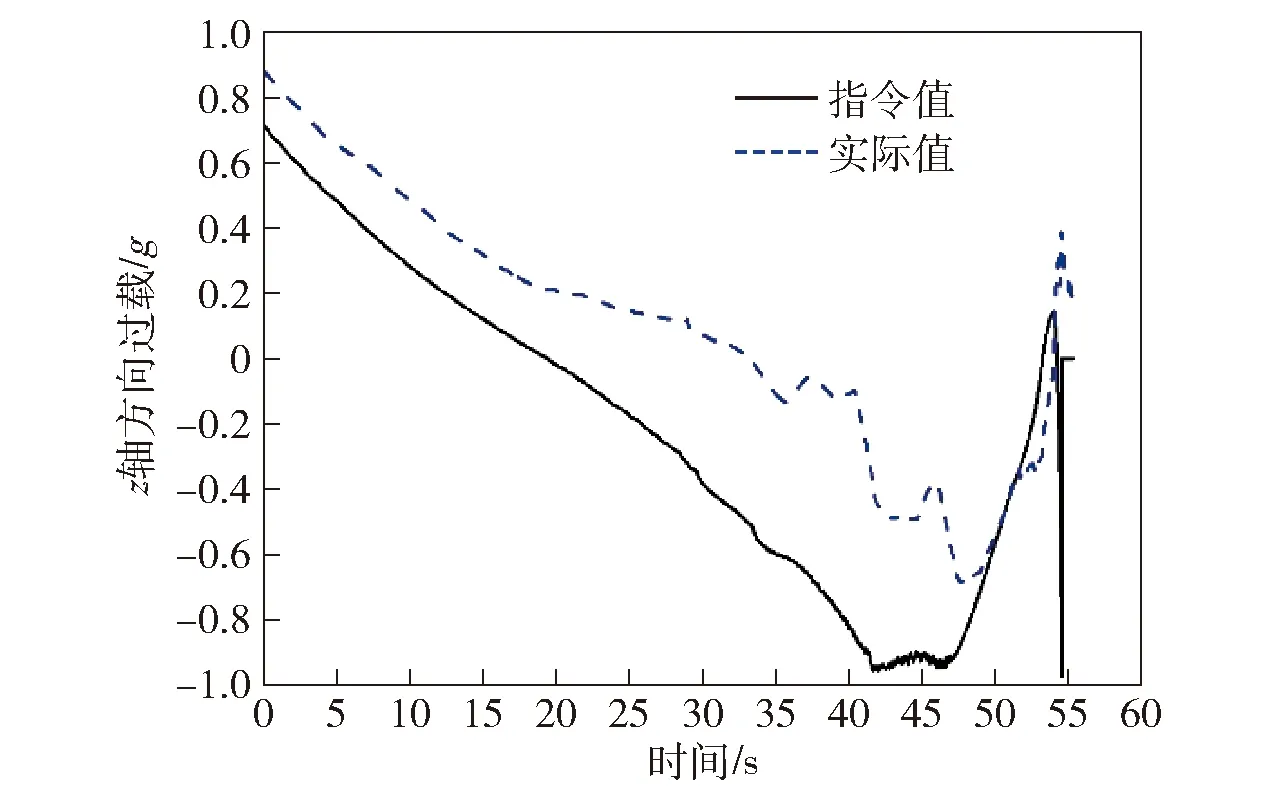
图18 模型存在不确定性时飞行器z轴方向过载响应曲线Fig.18 z-axis overload response curve of the model under uncertainties
4 结论
通常,飞行器处于大攻角飞行状态时,其三通道耦合严重,考虑到过载与姿态、姿态角速度、飞行速度、重力等多种因素有关,使得基于过载自动驾驶仪的控制系统设计较为困难。本文基于飞行器过载与姿态的等效转换,将过载指令转化为姿态指令,设计了以姿态反馈为主过载补偿为辅的控制系统,实现对过载指令的精确跟踪。
频域相位稳定性分析结果表明,通过设计满足频域稳定指标要求的校正网路和控制参数,本文方法能够实现对飞行器在偏差组合飞行状态下的稳定控制;飞行器6自由度仿真结果表明,本文方法既满足了制导对过载的跟踪精度要求,又达到了对飞行器姿态进行鲁棒稳定控制的目的。该方法简单可靠,具有良好的动态特性和很强的鲁棒性,已得到工程应用验证。

