主成分分析法在食品科学与工程专业学生成绩综合评价中的应用

陈向阳，吴永祥，毕淑峰，刘 板，胡晓倩

（黄山学院生命与环境科学学院，黄山 245041）

高等院校本科生在校就读期间要学习的课程数目多达60门以上，教师需要了解学生对所学理论知识与实践技能掌握的程度往往只是单一的分析某门课程，而忽视了各门课程之间的相关性。对于课程成绩的统计分析，基本上都是在期末考试结束以后分课程进行，很难从中获取较为全面有价值的信息，也没有办法解决学生各门课程之间的优势、劣势以及多门课程之间的相关性，造成教师给予学生的综合素质评价产生偏差。多年来，很多学者在科学、客观、公正、合理、有效地评估学生成绩方面做出了大量的研究，多元统计分析和正态分析的评价体系构建是相对集中研究点，在对学生成绩评价方面尤以多元统计中的主成分分析法应用较为广泛，同时主成分分析法也在不断创新与改进。文中的样本选择是以黄山学院食品科学与工程专业的主要核心课程的总评成绩，选取对象是2018级该专业的全部本科生，采用主成分分析法，借助DPS统计软件，分析14门核心主干课程之间的相关性以及学生个体在班级中的排名，从众多数据中寻找规律性的结论，去揭示学生成绩背后隐藏的内在教学规律，为食品科学与工程专业的教学质量的提高及因材施教提供科学的、有效的理论参考依据[1-3]。

1 主成分分析法的定义与具体步骤

1.1 主成分分析法的定义

主成分分析法是把原来众多指标转化为少数几个综合指标，考察多个变量间相关性的一种多元统计方法，尽可能地反应原来指标的信息，达到解释原来资料中的大部分变异。即从原始变量中导出相关性较大的几个主成分，让这几个主成分尽可能多地承载着原始变量的信息，同时彼此间互不相关的一种多变量分析方法[4-5]。

1.2 主成分分析法的具体步骤

具体步骤[6-9]：原始数据标准化；建立相关系数矩阵；计算各主成分的特征值、特征向量；依据特征值和累积贡献率确定所需的主成分因子数；计算主成分因子得分并排序。

2 结果与分析

样本选择是以黄山学院食品科学与工程专业的主要核心课程的总评成绩，选取对象是2018级该专业的全部本科生，由于在大一至大三这几年该专业共开设了60多门课程，从食品科学与工程专业视角进行初步遴选，以14门类主要专业核心课程总评成绩作为变量（如表1），建立一个65×14的原始各科成绩的样本数据矩阵，运用DPS数据处理软件对原始数据标准化处理，然后进行主成分分析，得到14门课程间的线性相关系数矩阵（如表2），得到14个主成分的特征值、方差贡献率和累计贡献率（如表3），计算前6个主成分分别对应的特征向量（如表4）。

表1 食品科学与工程核心课程

由表2可知，食品科学与工程专业的14门专业核心课程成绩之间的相关性只有大学英语（X1）和计算机基础（X13）之间表现为负相关，负相关不显著，表示大学英语与计算机基础之间不具有相互依赖性，剩下所有课程之间的相关系数均为正值，表现为正相关，说明彼此之间具有相互关联性，从表2还可以了解到大部分课程相互之间的相关系数大于临界值（p=0.05时，r=0.244；p=0.01时，r=0.317），达到了显著、极显著水平，各门课程成绩间具有较强的可比性与依赖性。在这些课程中，发现食品分析（X7）、食品安全学（X10）之间的相关系数达到最高（0.782），二者之间相关性达到极显著，表明这两门课程之间有很强的可比性与依赖性。食品工程（X4）、食品保藏学（X9）、食品安全学（X10）与其他课程之间的相关系数均达到0.317以上，即相关性达到极显著水平，这也充分说明了这几门课程成绩对其他核心主干课具有较强的相互依赖性，有力地验证了食品工程、食品保藏学、食品安全学的学习能力对食品科学与工程专业本科生有着较大影响。

此外，大学英语（X1）与计算机基础（X13）、有机与无机化学（X2）之间的相关系数较小，相关性均不显著，这3门课程是公共必修课，可能影响着学生的进一步升学与工作，在日常的教学中教师可以应用相关案例分析，积极引导学生对这些公共必修课的重视。

根据表3所示结果可知，第一主成分的特征值高达7.242，方差贡献率高达51.726%，即第一主成分可以反映学生成绩的主要信息量。前6个主成分的累积方差贡献率也达到了82.212%。若运用主成分分析中方差贡献率不小于80%的判断标准，前6个主成分就能很好地概括所选的14门课程学生成绩的信息量。若按照特征值大于1的标准确定主成分个数，则仅需前 2个主成分就能较好地概括这组数据的信息，基本满足学生成绩综合评价要求，实现了降维分析，大大简化了数据结构。

表3 基于学生成绩的各主成分特征值、方差贡献率和累积贡献率

根据表4所示结果可知，第一主成分对应的特征向量均为正值，数值上相差较小，说明第一主成分可以反映学生在14门核心课程上的综合学习能力。分析比较第一主成分的14个特征向量大小发现，高等数学（X12）超过了有机与无机化学（X2），而与食品微生物学（X6）权重相近。有机与无机化学相对于高等数学这门课程，较为传统的观点认为与食品相关专业课程学习更具有基础性和必要性，通过高等数学在第一主成分的权重，揭示了这种看法具有片面性。实际上，学好高等数学这门课程能够使工科专业学生逻辑思维和推理能力得到训练，有利于培养学生分析和解决问题能力。

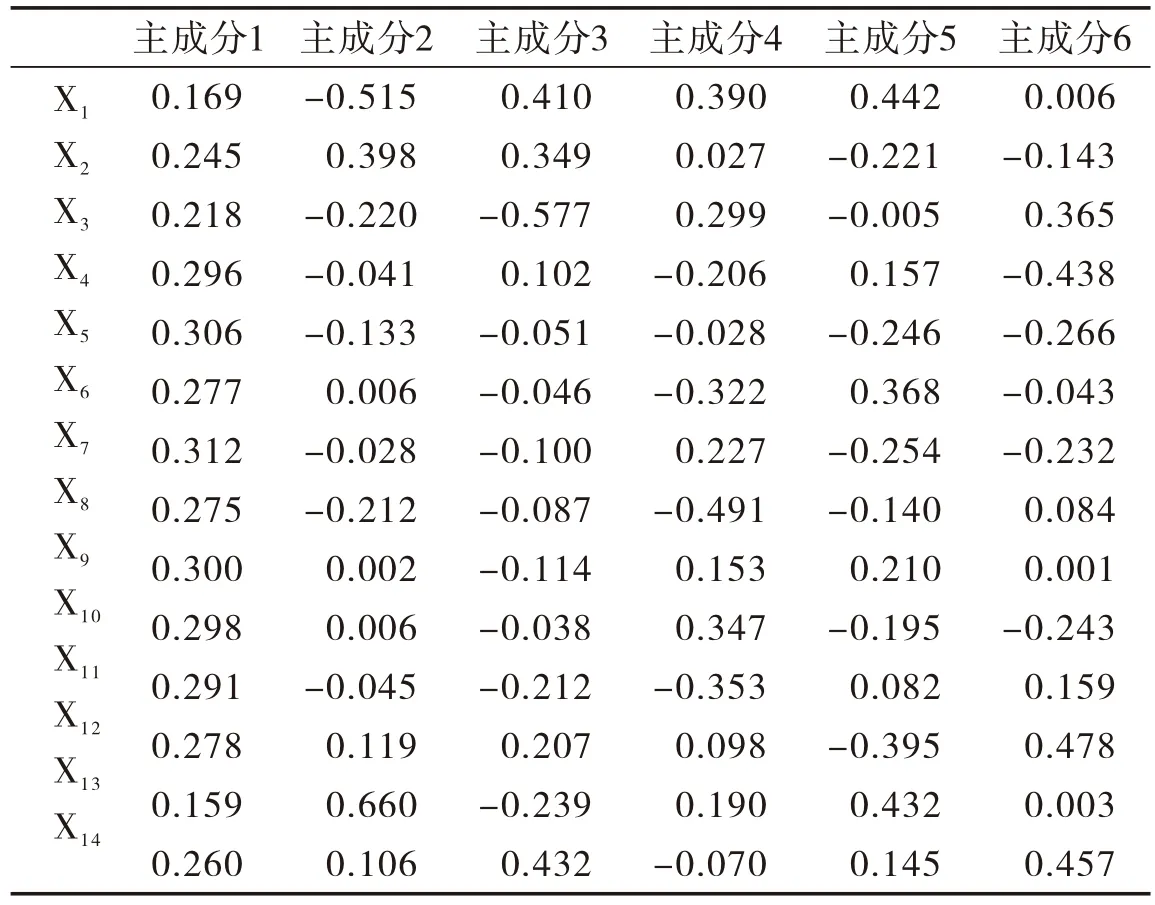
表4 前6个主成分分别对应的特征向量

由表4可知，第一主成分在食品工程（X4）、食品化学（X5）、食品分析（X7）、食品保藏学（X9）、食品安全学（X10）、食品营养学（X11）课程上的特征向量分值较大，即承载的信息量较大，这6门课程能基本概括学生的综合学习能力，可以代表学生的专业课掌握情况。第二主成分的方差贡献率8.759%，相对较小，且在各门课程上的特征向量有正有负，如果单独采用第二主成分分析学生潜在的学习能力容易产生偏差。其余的4个主成分情况与第二个主成分类似，因此采用第一主成分分析与评价学生综合学习能力相对较为客观。

依据表4得到前6个主成分分析结果，计算学生在第一主成分的得分情况可采用如下表达式（其他主成分得分计算以此类推）：

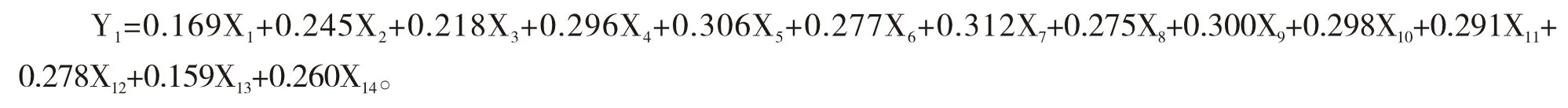
计算前6个主成分综合得分，其表达式如下：

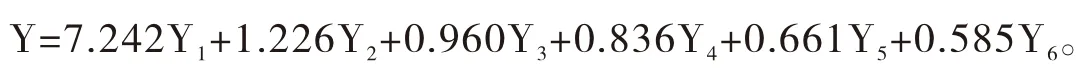
将每位学生的课程成绩标准化后的数据代入Y1、Y2、Y3、Y4、Y5、Y6和Y的表达式中，得到65名学生在6个主成分的得分与综合得分，同时将65名学生的主成分得分、综合得分、平均分分别进行排名，结果见表5所示。通过表5可以明显看出65名学生在第一主成分得分排名与前6个主成分的综合得分排名和平均分排名十分接近，这就说明在学生综合学习能力评价方面即使是采用第一主成分给出的信息也能满足实际需要。在实际应用中主成分分析法与简单地进行算术平均数排序方法相比，可以进一步判断学生在综合学习能力和学科上的优劣，结果更具科学性和客观性。

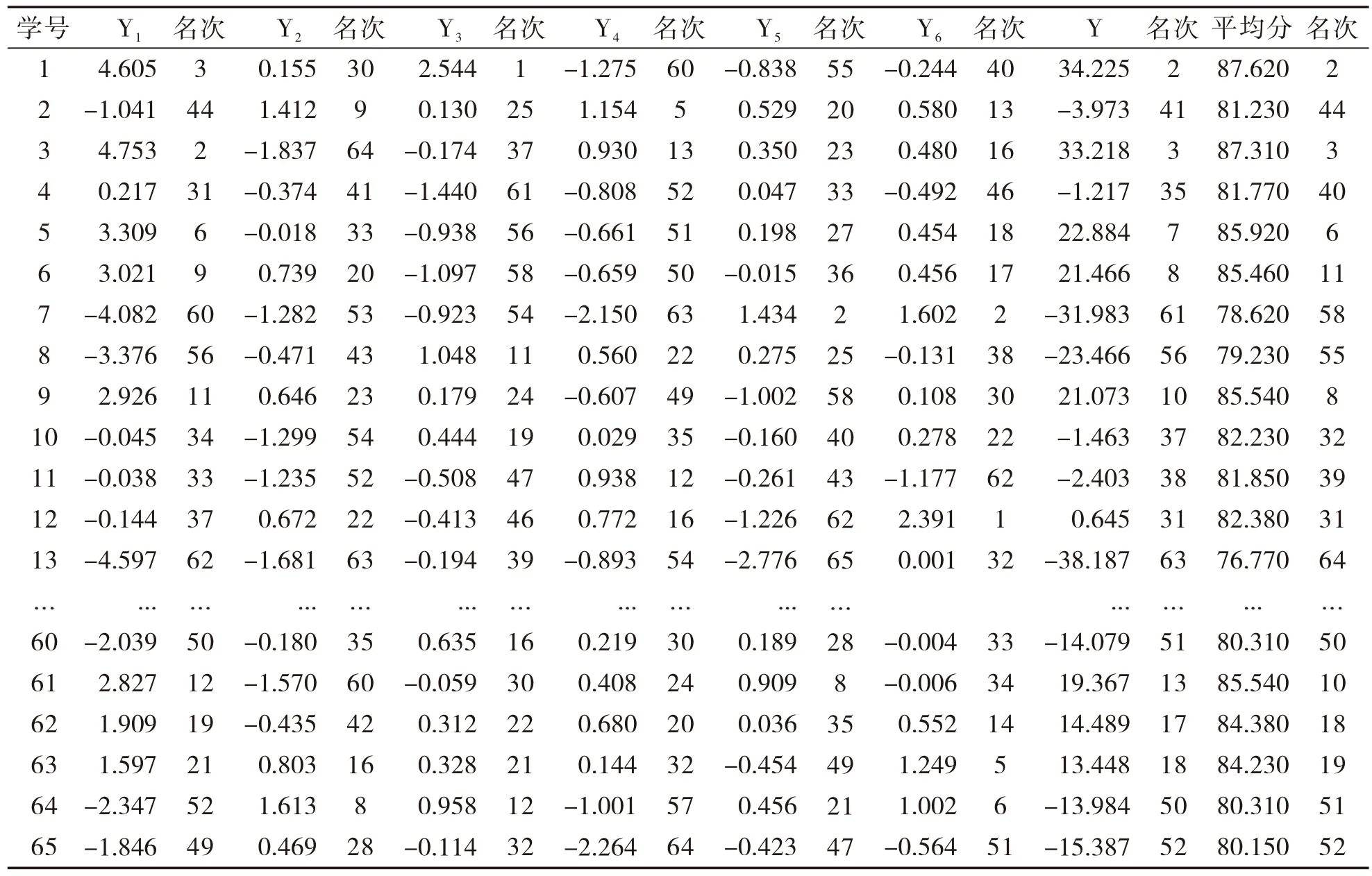
表5 主成分因子得分、综合得分、平均分排名

3 结 论

将多元统计思想应用到学生综合学习能力的评价中，运用主成分分析统计方法，建立主成分模型，借助DPS数据处理软件，依据学生课程成绩原始样本数据挖掘出了多条潜在的有价值信息，如从各门课程线性相关性分析中得出食品工程、食品化学、食品分析、食品营养学、食品保藏学、食品安全学等课程在培养食品科学与工程专业学生的专业技能与综合素质具有重要作用。第一主成分承载着学生成绩的较多潜在信息，应用主成分评价学生的学习能力比课程平均成绩所呈现的学习素质优劣更具科学性和客观性，为因材施教提供科学依据。选修课和专业限选课对学生综合能力的提升的影响在文中没有进行数据选取和统计分析，有待于后期将进一步研究。通过以上的分析认为，主成分分析法可应用于食品科学与工程专业课程培养方案评估与改进分析，为本专业人才培养目标的实现将会起着一定的作用。