一种基于圆环模型的网格搜索定位算法*
王浩祥,邓 平
(西南交通大学 信息编码与传输重点实验室,成都 610031)
0 引 言
随着信息行业的不断发展,人们对全区域精准定位的需求越来越大。虽然如今的基站(Base Station,BS)建设已经可以满足大部分区域被三个或三个以上的BS覆盖,但是仍有小部分偏僻区域只能被两个BS覆盖,所以研究双基站场景的非视距定位算法对于实现全区域的精准定位具有重大意义。文献[1]利用BS测得的电波到达角(Angle of Arrival,AOA)信息对散射体进行定位,然后将散射体作为虚拟基站进行网格搜索,最后将符合条件的网格点约束平均得到移动台(Mobile Station,MS)位置。文献[2]根据先验的建筑信息模型,将建筑模型的几何约束信息加入到原有的优化问题中,较好地提升了定位性能。文献[3]针对内点法局部最优性质,提出了一种网格搜索方法,设立两个误差因子,根据误差因子的上下限设置网格区域,将网格内满足约束的点平均后得到MS位置。文献[4]根据先验的基站周围的空间布局确定出散射区域并构建散射区模型,然后将聚类算法与几何模型结合构建优化问题,最后根据最优化理论求解移动台的位置。
在针对特定的散射体分布模型的研究中,文献[5]提出了基于圆环模型的混合定位算法,通过不断迭代的方式确定散射半径。算法需要6条多径信号的到达时间(Time of Arrival,TOA)信息和AOA信息,并且要求散射体散射的信号被两个基站同时接收到,条件比较苛刻。文献[6]提出了针对指数分布和高斯分布的迭代求取移动台位置的算法。虽然针对特定散射模型的算法精度不错,但是复杂度较大。
在近几年的少基站无线定位研究中,一般会加入一些额外的辅助信息或者特定的约束来进行定位。文献[7]仿真对比了电波到达角信息、电波离开角信息以及最大散射半径分别对定位性能的影响。另外,部分算法根据不同基站之间距离[8]或者基站与待测点之间的距离[9]确定不同基站的权重系数,利用权重系数的差距来提升定位的准确性。文献[10]提出了一种虚拟基站定位算法,在假定最大散射半径的条件下估计出散射体位置,然后视散射体为虚拟基站来约束移动台位置范围,最后在网格区域内搜索移动台位置。
本文针对目前抗非视距定位算法存在需要的基站数目过多、多径信号数目过多的问题,提出了一种基于圆环模型的网格搜索定位算法。仿真结果表明,与现有算法相比,本文所提算法具有更好的定位性能。
1 基于圆环模型的混合定位算法
当散射模型处于一种特定的模型时,比如圆环分布、圆盘分布等,用特定的算法可以根据不同散射模型的几何约束条件更好进行定位,如HRB(Hybrid TOA/AOA Ring Based)算法就是一种基于圆环模型的混合定位算法[5]。
由图1可以看出HRB算法适用于双基站环境,需要的散射体数量为3个或3个以上,散射体的分布需要符合圆环分布模型。算法进行定位需要6条多径信号的TOA和AOA信息。αij代表基站BSj收到的来自散射体Si的多径信号AOA值,Lij代表基站BSj收到的来自散射体Si的多径信号TOA值,R为圆环散射模型的半径。
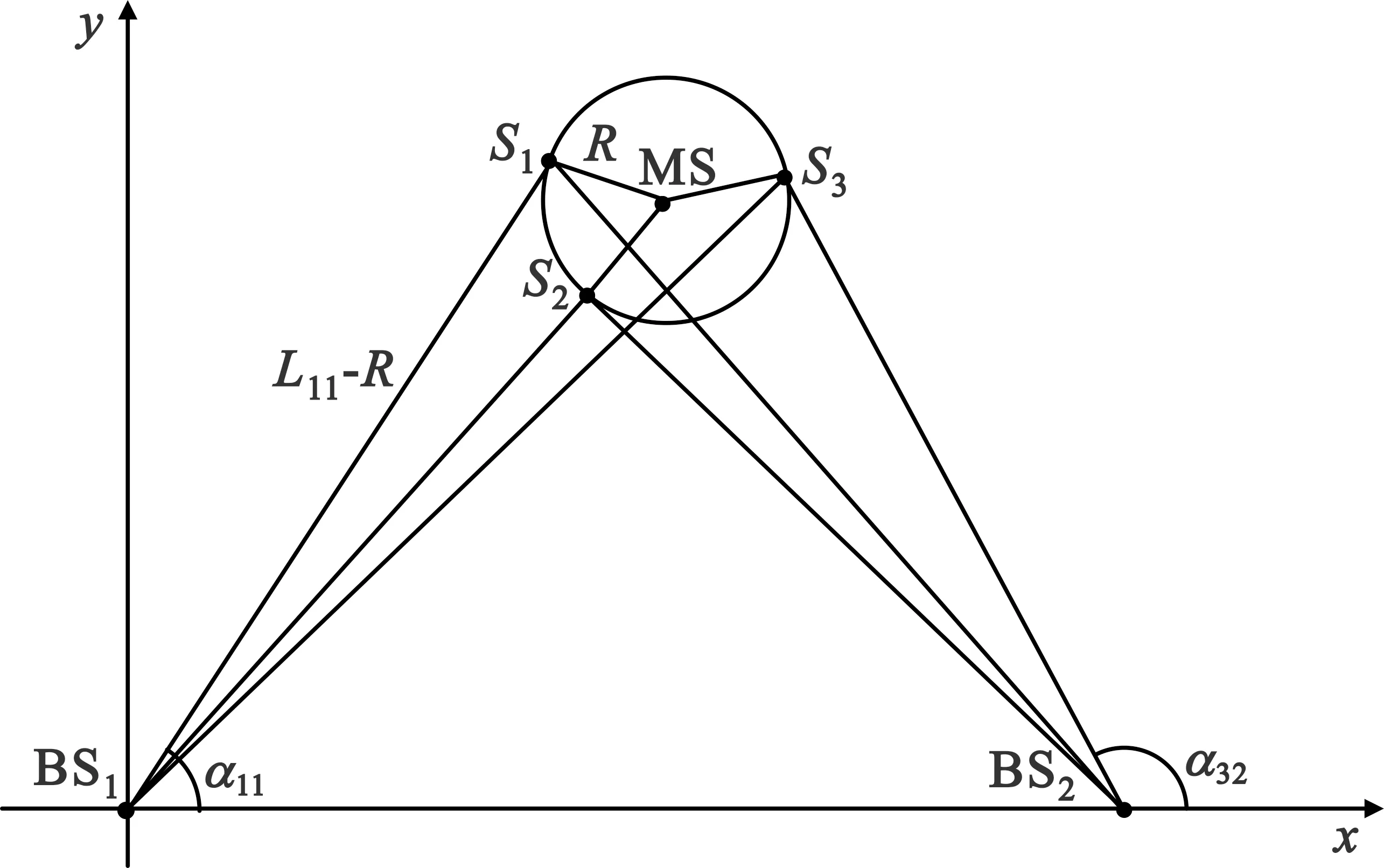
图1 基于圆环模型的几何分布示意图
根据圆环散射模型的几何特征,基站到散射体的距离可以表示为dij=Lij-R,散射体的坐标(xij,yij)可以根据dij、αij、基站BSj的横坐标xbsj和基站BSj的纵坐标ybsj进行计算:
(1)

2Aθ=b。
(2)
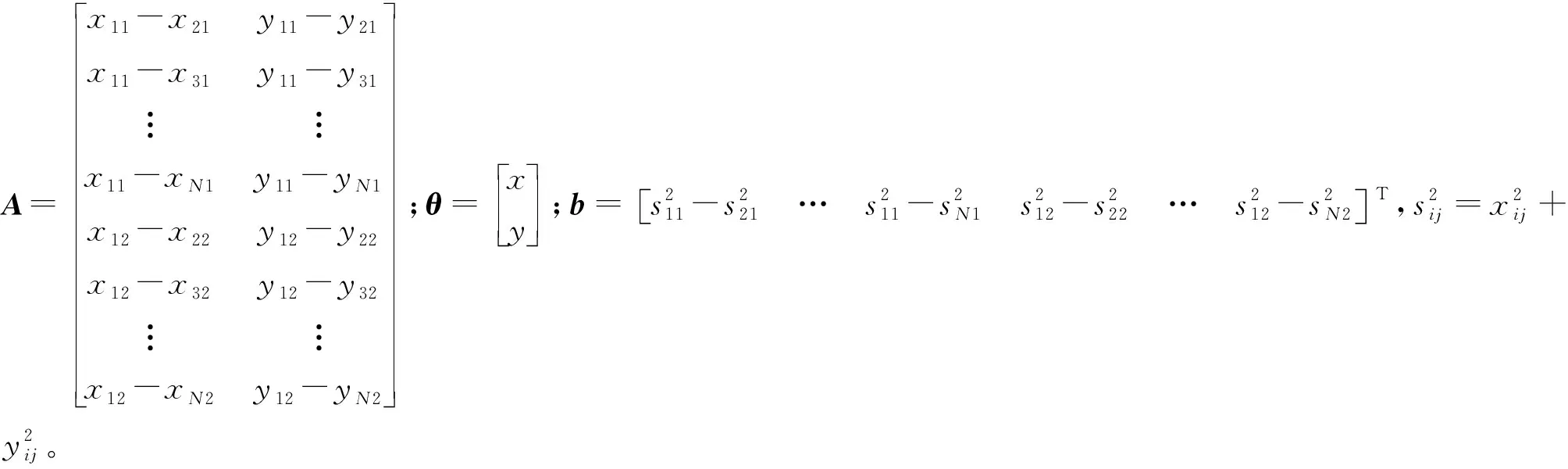
(3)
HRB算法的主要步骤如下:
Step1 假定散射体半径R的初始值。
Step2 根据每个基站的测量TOA值和AOA值通过式(1)计算散射体的坐标。
Step3 根据式(3)计算移动台MS的坐标。
Step4 根据更新的MS坐标计算散射体半径R的更新值。
Step5 计算更新的散射体半径与原有的散射体半径差值是否小于设定的阈值,若大于则用更新之后的R返回Step 2,继续迭代;若小于则停止迭代,当前步骤求得的MS坐标即为最终值。
2 基于圆环模型的网格定位算法
本文根据现有的双基站定位算法,提出了一种改进的TOA/AOA混合定位算法。算法应用于双基站定位环境,需要的散射体数量为3个或3个以上,散射模型为圆环散射模型,要求多径信号数目在3条或3条以上。算法将虚拟基站思想与网格搜索算法相结合,主要流程分为三步:首先进行散射体位置的确定;其次对移动台的位置进行网格搜索;最后将所有候选点根据定义的误差目标函数的大小进行选择性平均。
2.1 散射体位置的确定
参考HRB算法的迭代改变散射半径的方式,本文将迭代改变散射半径的方式改为搜索散射半径的方式。本文算法将HRB算法所需要的多径信号数量从6条降低到了3条,并且解决了两个基站要同时检测到来自同一散射体散射的信号这一问题。
图2是散射体数量为3个时,基站、散射体和移动台的几何分布示意图,基站BS1检测到了来自两个散射体散射的多径信号,BS2检测到了来自剩下散射体散射的多径信号。根据圆环散射模型的几何特征,基站测得的距离测量值减去R可得基站与散射体的距离,然后根据测量距离和AOA测量值求出散射体坐标。

图2 算法几何分布示意图
已知散射体坐标后,根据移动台到各个散射体的距离均为R可设立等式方程,对MS的求解公式为
(4)
搜索散射半径的主要步骤如下:
Step1 先假设一个圆环散射半径的初值R,一般从0开始。
Step2 将散射体半径R和基站检测到的TOA、AOA信息代入式(1)求解散射体的坐标。
Step3 根据式(4)的最小二乘法,求出移动台的坐标。
Step4 求出移动台与所有散射体的距离,判断这些距离与R的差值是否都小于设定的阈值,若小于则跳出循环,当前散射半径和散射体坐标即为所求;若大于则将R增大一定的步长,再从Step 2开始循环。
2.2 网格搜索并筛选候选点
当完成了散射体位置的确定,接下来便是网格区域的确定和候选点的筛选。文献[10]利用了先验的最大散射半径这一信息,对散射体位置进行求解,再利用最大散射半径信息进行网格区域的确定与搜索。本文并没有假定最大散射半径这一限制,在确定散射体坐标后,将3个散射体作为虚拟基站,以搜索好的R作为当前虚拟基站得到的TOA值。如图3所示,移动台的位置位于以虚拟基站VBSi为圆心、以圆环散射半径R为半径的定位圆交叠域内,即图3中的阴影区域。
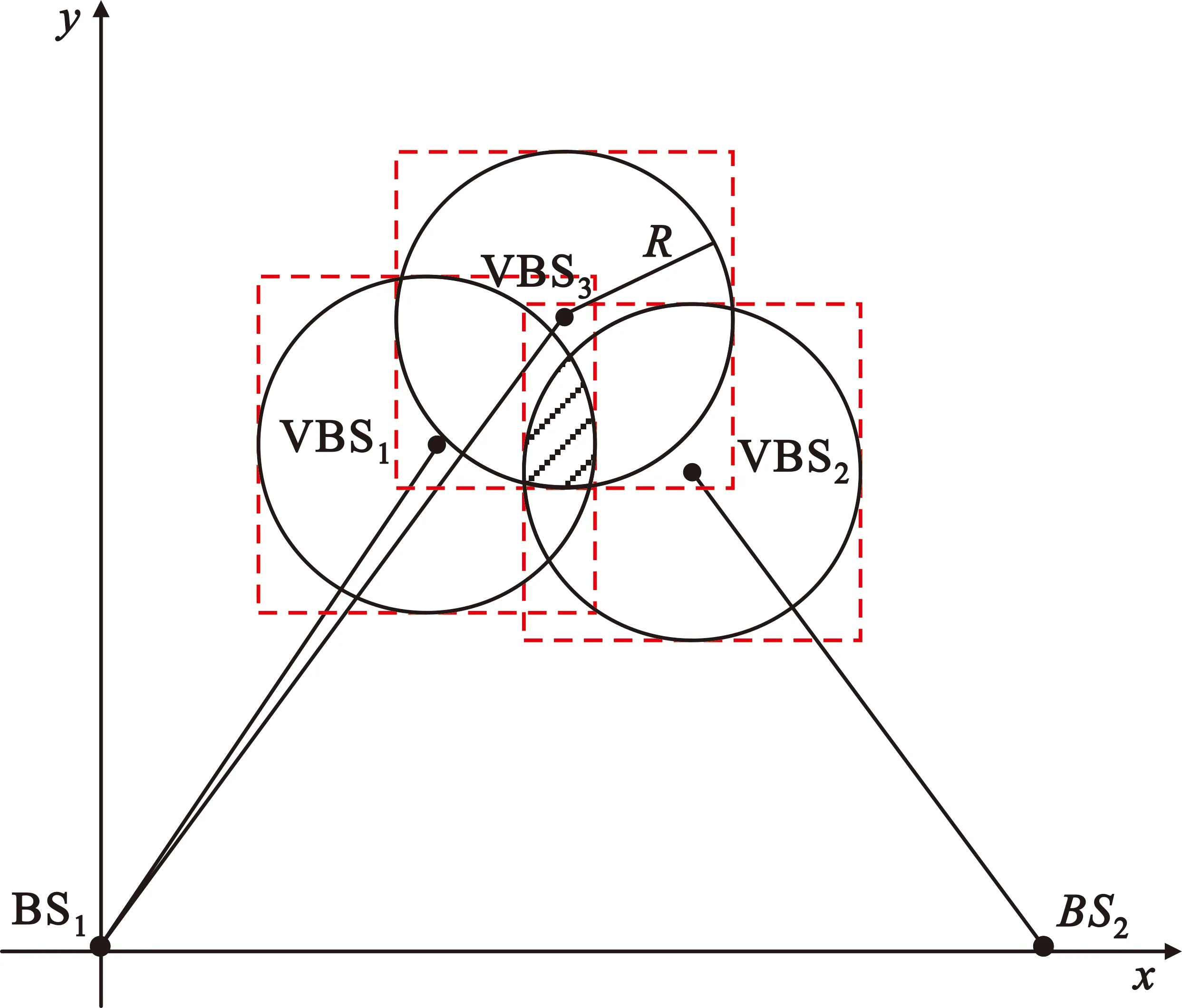
图3 虚拟基站定位示意图
由于图3中的阴影区域难以确定边界,所以将图3中的三个圆交叠的阴影区域放大到如图3所示的三个矩形区域的交叠区域,这样可将网格搜索的区域设定为长方形,方便进行遍历搜索。即移动台位于以虚拟基站VBSi位置坐标(xVBS,i,yVBS,i)为中心、以2R为边长的矩形交叠区域内,从而获得MS位置范围为
(5)

(6)
(7)

2.3 选择性平均
在得到K个MS的可能位置候选点后,根据最优化定位技术的思想,构建出误差目标函数:
(8)
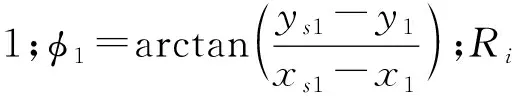
(9)
li=dms,si+ds,i=

(10)
将得到的MS的可能位置候选点代入式(8)进行求解,然后根据目标函数F(x,y,Ψs)的大小进行排序,排序后舍去较大的K/2个值(向下取整),最后将剩下的目标函数的值对应的可能位置候选点坐标进行算术平均,得到最终的MS位置坐标。
综上,本文提出的算法流程如图4所示。

图4 算法流程图
3 算法仿真与性能分析
本文仿真过程是在Matlab软件下进行的,挑选双基站环境下的5种算法进行比较:HTA(hybrid TOA/AOA algorithm)算法、TACA(TOA/AOA Constraint Algorithm)算法、网格搜索算法(Grid Search Algorithm,GSA)[3]、HRB算法以及本文的改进算法。几何分布图如图3所示。散射体模型为圆环模型,基站数量为2个,坐标分别为BS1(0,0)、BS2(1 732,0),单位m。蜂窝网的半径为1 000 m,移动台坐标为
(11)
通过使用无线定位中常用的均方根误差(Root Mean Square Error,RMSE)、平均定位误差(Average Location Error,ALE)和累积分布函数(Cumulative Distribution Function,CDF)三种评判指标来进行不同算法之间的性能比较。
固定角度测量误差服从均值为0、标准差为1°的高斯分布,距离测量误差服从均值为0、标准差为5 m的高斯分布,散射体半径R作为变量,取值依次分别为100 m、150 m、200 m、250 m、300 m,独立仿真1 000次,5种算法的ALE曲线和RMSE曲线分别如图5和图6所示。由图可见,随着散射半径的增大,各个算法的性能都有所下降,主要是因为传播距离变长,NLOS误差变大。本文算法具有较小的平均定位误差和均方根误差,并且与其他算法定位误差差距较为明显,充分体现了本文算法对NLOS误差的适应性优于对比的其他算法。
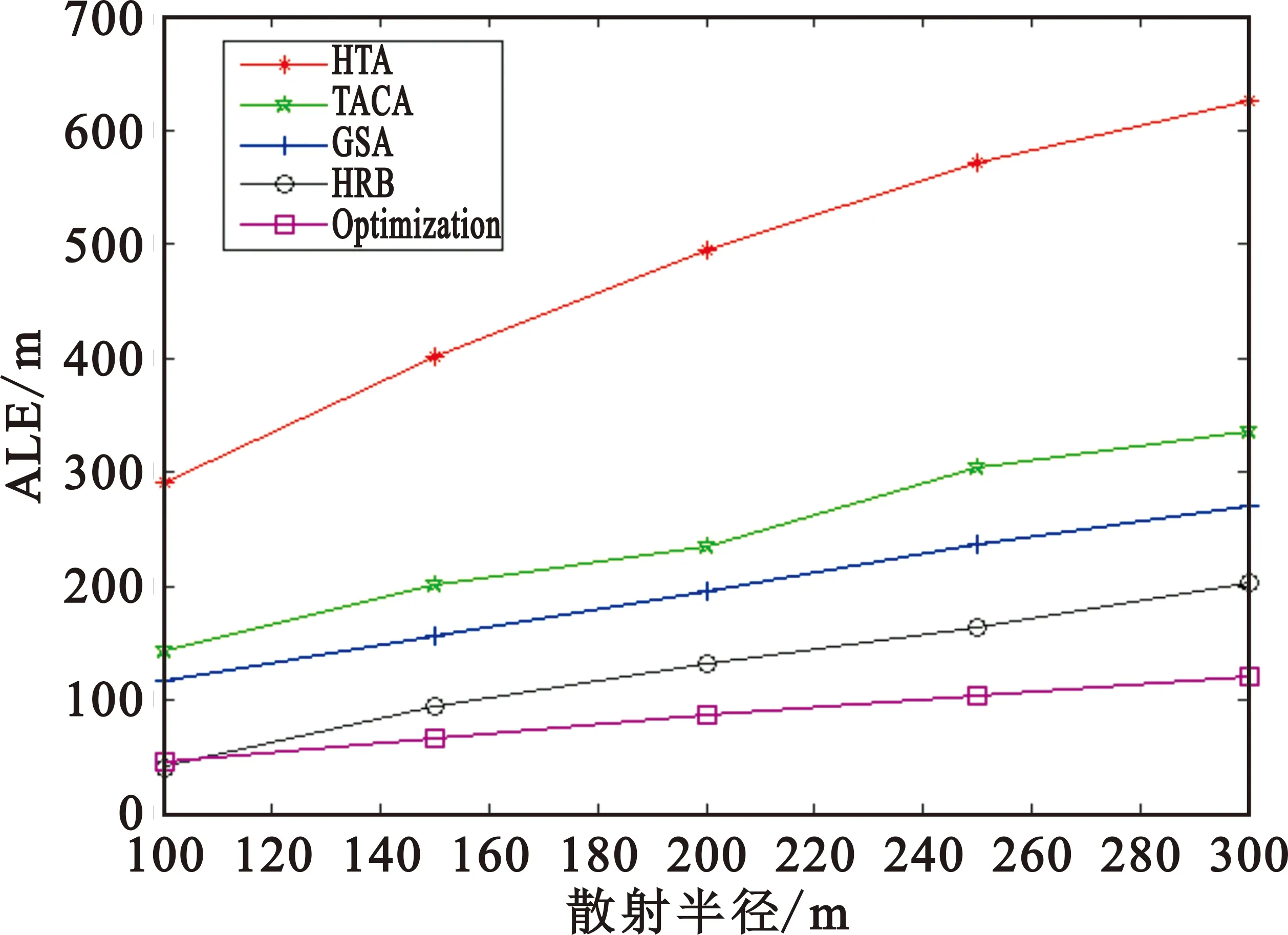
图5 ALE随散射半径的变化
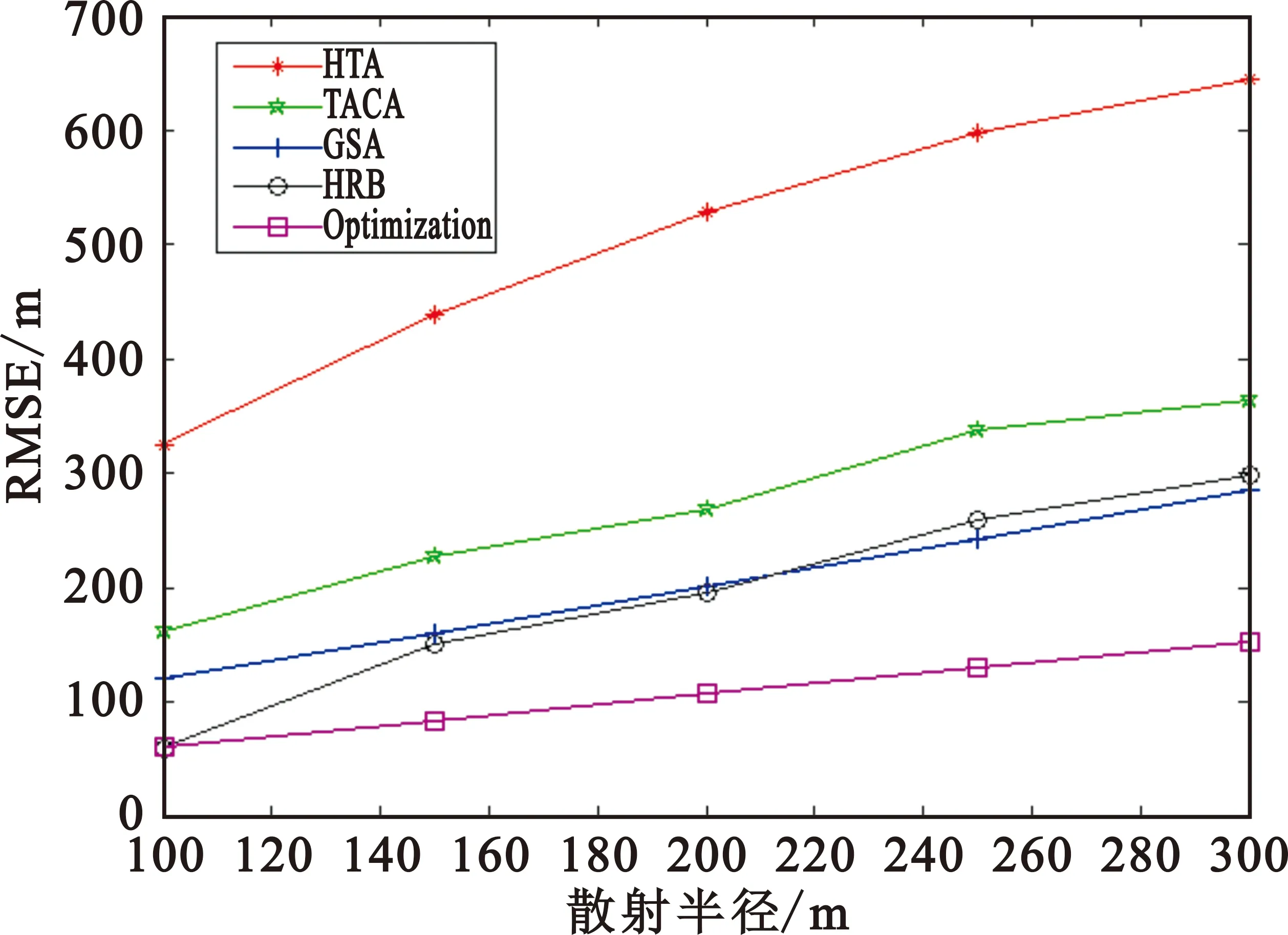
图6 RMSE随散射半径的变化
固定距离测量误差服从均值为0、标准差为5 m的高斯分布,散射半径设置为200 m,将角度测量误差作为变量,均值为0,标准差依次取值0.5°、1°、1.5°、2°、2.5°,独立仿真1 000次的ALE曲线如图7所示。由图可以看出,随着AOA测量误差的增大,对比算法的性能变化不大,但是HRB算法和本文算法的误差有较小的增大。这主要是因为这两种算法在定位散射体时用到了基站的AOA测量值,该测量值的准确性可以影响散射体的坐标估计准确性。从仿真图可以看出本文算法的定位性能依然优于对比算法。
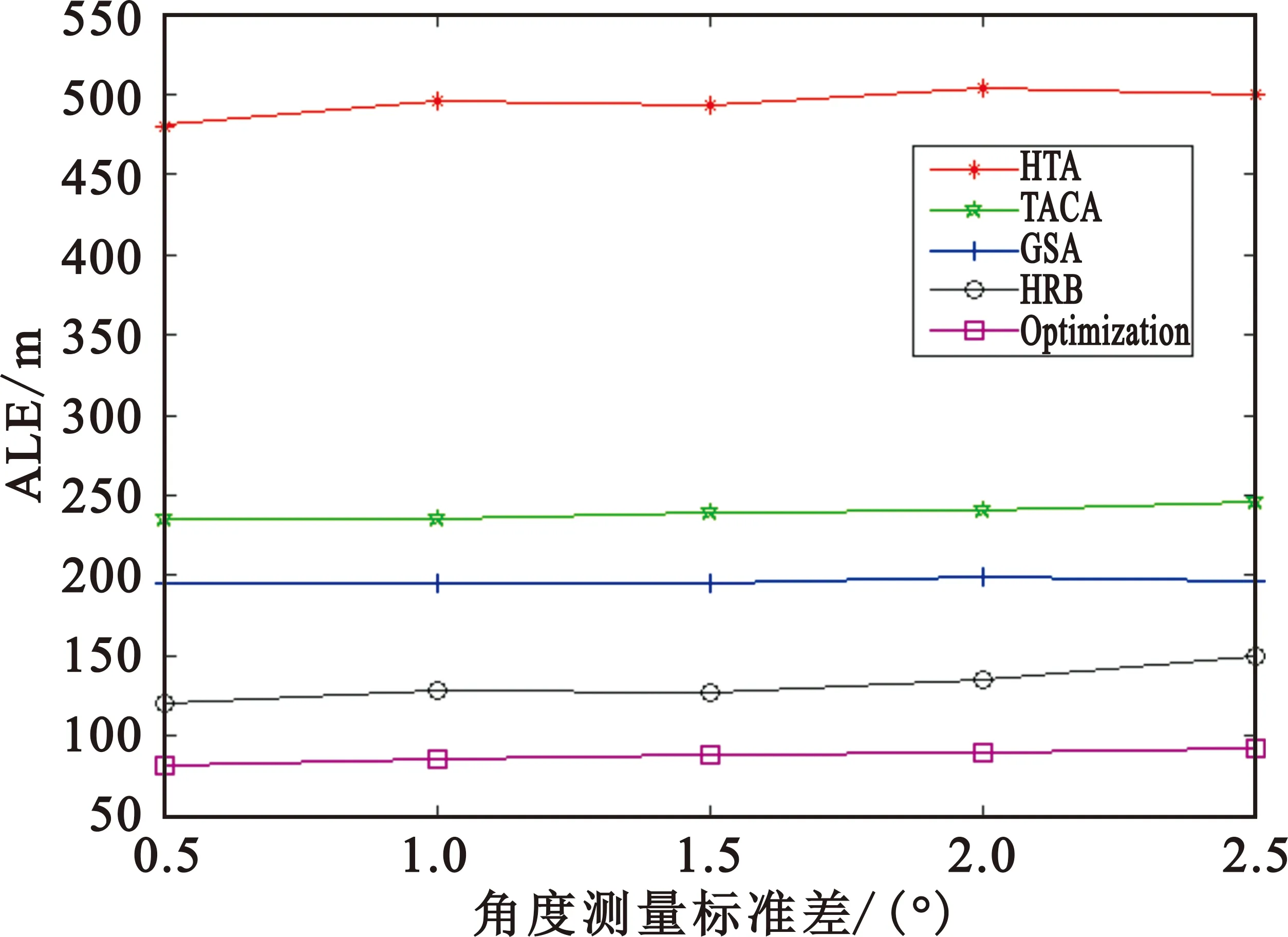
图7 ALE随角度测量误差的变化
固定角度测量误差服从均值为0、标准差为1°的高斯分布,散射半径设置为200 m,将距离测量误差作为变量,均值为0,标准差依次取值2 m、4 m、6 m、8 m、10 m,独立仿真1 000次的ALE曲线如图8所示。由图可以看出,算法对TOA测量误差都不敏感,在不同的TOA测量误差情况下本文算法性能优于对比算法。
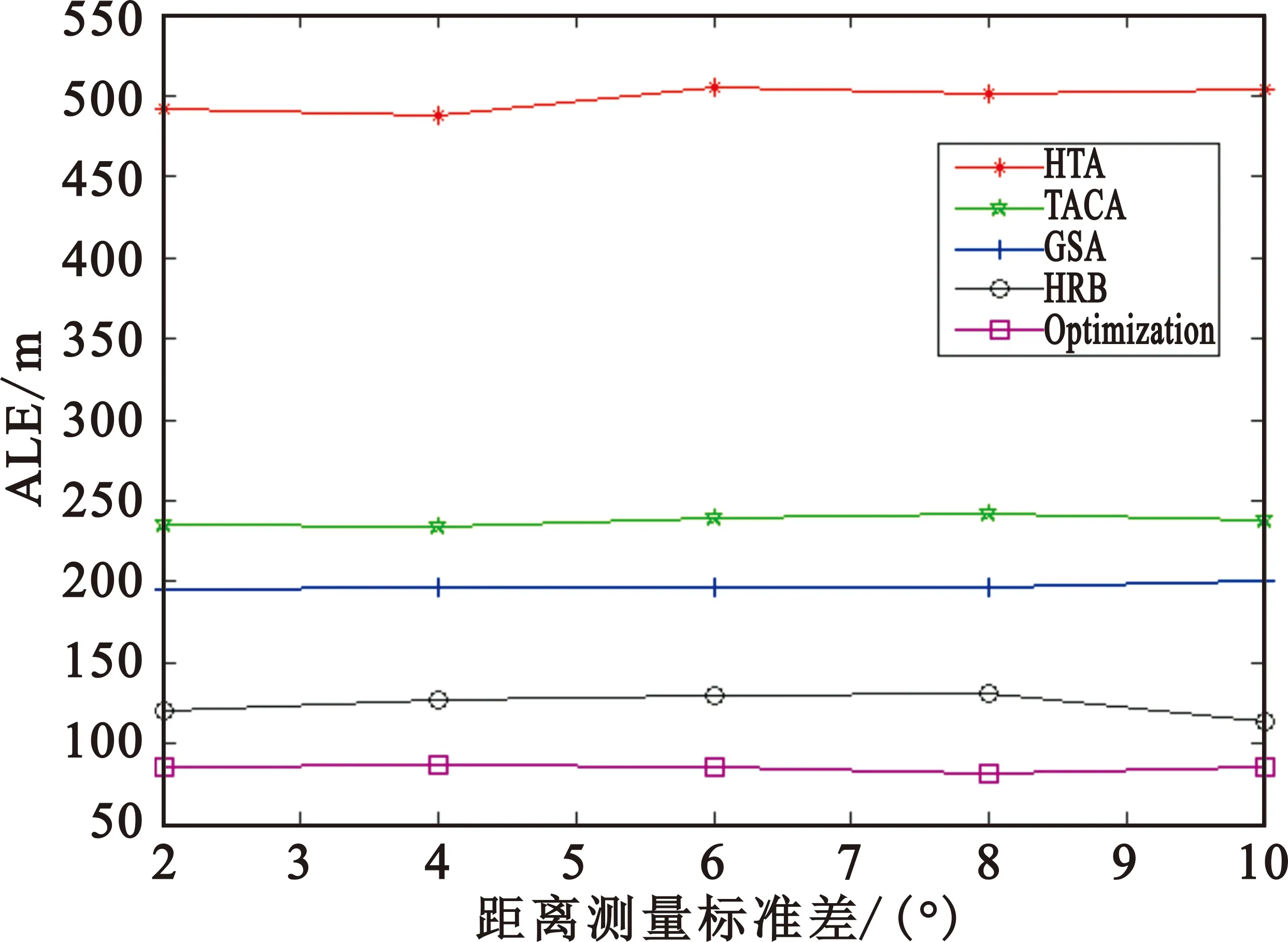
图8 ALE随距离测量误差的变化
固定角度测量误差服从均值为0、标准差为1°的高斯分布,距离测量误差服从均值为0、标准差为5 m的高斯分布,散射半径设置为150 m,5种算法的误差累积分布函数曲线如图9所示。由图可以看出本文算法的平均定位误差小于200 m时CDF可达到100%,表现出了较强的鲁棒性,这主要是由于网格搜索法与选择性平均结合使用的效果。实验结果证实了本文算法的有效性。

图9 圆环模型下累计分布函数曲线图
固定散射模型的两种算法利用了散射模型的几何关系,在先验条件上比HTA、TACA和网格搜索算法多,所以整体上看,固定散射模型的两种算法性能好于另外的三种算法。
从仿真图可以看出改进的算法性能明显好于传统的最优化定位算法以及HRB算法。虽然改进算法和HRB算法都是基于固定散射模型的算法,但是改进算法只使用了3条多径信号的信息,而HRB算法使用了6条,并且要求散射体散射的信号同时被两个基站都检测到,条件比较严苛。从算法理论的角度分析,本文算法先是通过圆环模型的几何特征和基站测量值信息确定出散射体坐标,然后根据虚拟基站技术可以减少非视距误差的特性,将散射体视为基站进行后续的定位。算法后续的网格搜索定位法是一种直接利用约束条件进行定位的最优化理论算法,相较于对比的最优化内点法,既降低了算法复杂度又解决了内点法局部最优的情况。
改进算法利用圆环模型的几何特性,先比较精准地定位了散射体位置,在基于比较精准的散射体位置的基础上将网格搜索法和选择性平均结合,很好地提升了定位性能。
4 结 论
为提升文献[5]提出的基于固定散射模型的HRB算法的性能,本文先利用圆环模型的几何特征,搜索圆环的半径,根据圆环的半径、TOA信息和AOA信息确定散射体的位置;然后将散射体作为虚拟基站来约束MS可能位置范围,并使用网格搜索来获得多个MS可能的估计位置;最后根据目标函数的大小进行选择性平均。不同NLOS场景下的仿真结果表明,本文算法的定位误差相较于文献[5]算法有明显减少,同时也要显著优于其他现有算法,验证了算法的有效性。

