任务迁移的移动边缘计算系统中资源分配和任务卸载策略*
贾淑霞,郝万明,高梓涵,杨守义
(郑州大学 信息工程学院,郑州 450001)
0 引 言
随着5G网络的普及,计算密集型的移动应用将不断增加,但移动设备可能不足以支撑这些应用的计算需求,移动云计算(Mobile Cloud Computing,MCC)应运而生。虽然MCC具有高存储能力和强大计算能力等优点,但是它增加了前向链路传输延时,对延时敏感应用(如人脸识别、自动驾驶交互式情景在线游戏等)并不适用。为降低传输延时,有学者提出移动边缘计算(Mobile Edge Computing,MEC)[1-2],将计算密集型任务卸载至距离终端较近的移动网络边缘进行处理,可同时满足用户快速交互响应和灵活计算服务的需求,缓解了核心网络的压力。
MEC系统主要涉及计算任务卸载策略的研究,其性能的好坏一般是以时延或能耗为衡量指标,目前卸载策略依照需求可分为最小化时延、最小化能耗以及均衡能耗和时延,但这些策略未考虑计算任务的执行机制,将计算任务看作一个整体,即为粗粒度卸载。而在实际生活中,任务之间是存在依赖性的,例如通过智能手环分析人的睡眠状态,首先传感器根据手腕的动作幅度和频率采集运动数据,然后系统根据传感器反馈的数据进行计算来衡量睡眠的质量,即任务间存在依赖关系,为细粒度卸载。此外,任务卸载并非静态过程。文献[3]中提出了一种新的移动感知编码概率缓存方案使得吞吐量最大,文献[4-5]只考虑了移动用户的移动性,并未涉及用户能耗与时延需求且未考虑任务之间的依赖性。
为了更好地符合实际通信场景,本文考虑了任务之间的依赖性,并针对在任务卸载时由于设备的移动而导致任务迁移这一问题建立了任务迁移模型,提出通过优化资源分配和任务卸载策略来解决基于联合时延和能耗的损耗函数最小的优化问题。仿真结果表明本文提出的算法能够以更小的损耗提升系统性能。
1 模型建立
1.1 系统模型
本文假设一个移动用户可以被相邻两个边缘云服务,且边缘云之间通过宏基站(Macro Base Station,MBS)互联,从而实现任务的相互迁移。迁移是指任务在未完成卸载时离开当前边缘云而导致数据在边缘云之间的迁移,即卸载至边缘云1的任务在未完成计算之前,设备已移出边缘云1的服务范围内转而进入边缘云2服务范围,从而边缘云1的任务计算结果会通过MBS迁移到边缘云2,然后返回至终端。系统模型如图1所示,由两个边缘云服务器和若干应用组成。假设移动应用包括一组子任务,每个子任务按顺序依次进行,即下一个子任务需在上一个子任务完成后才能进行。在该系统中,每个应用被划分成任务序列N,用集合N={1,2,3,…,N}表示。其中任务间的依赖性不可忽略,本文子任务的依赖模型为顺序进行,因此采用有向无环图进行描述,用G(N,E)表示。用E表示调用依赖关系,E={e|e=e(i,j),i,j∈N},其中i∈N代表每个任务,e(i,j)表示任务的先后顺序,即任务j要等到i完成后才能执行。
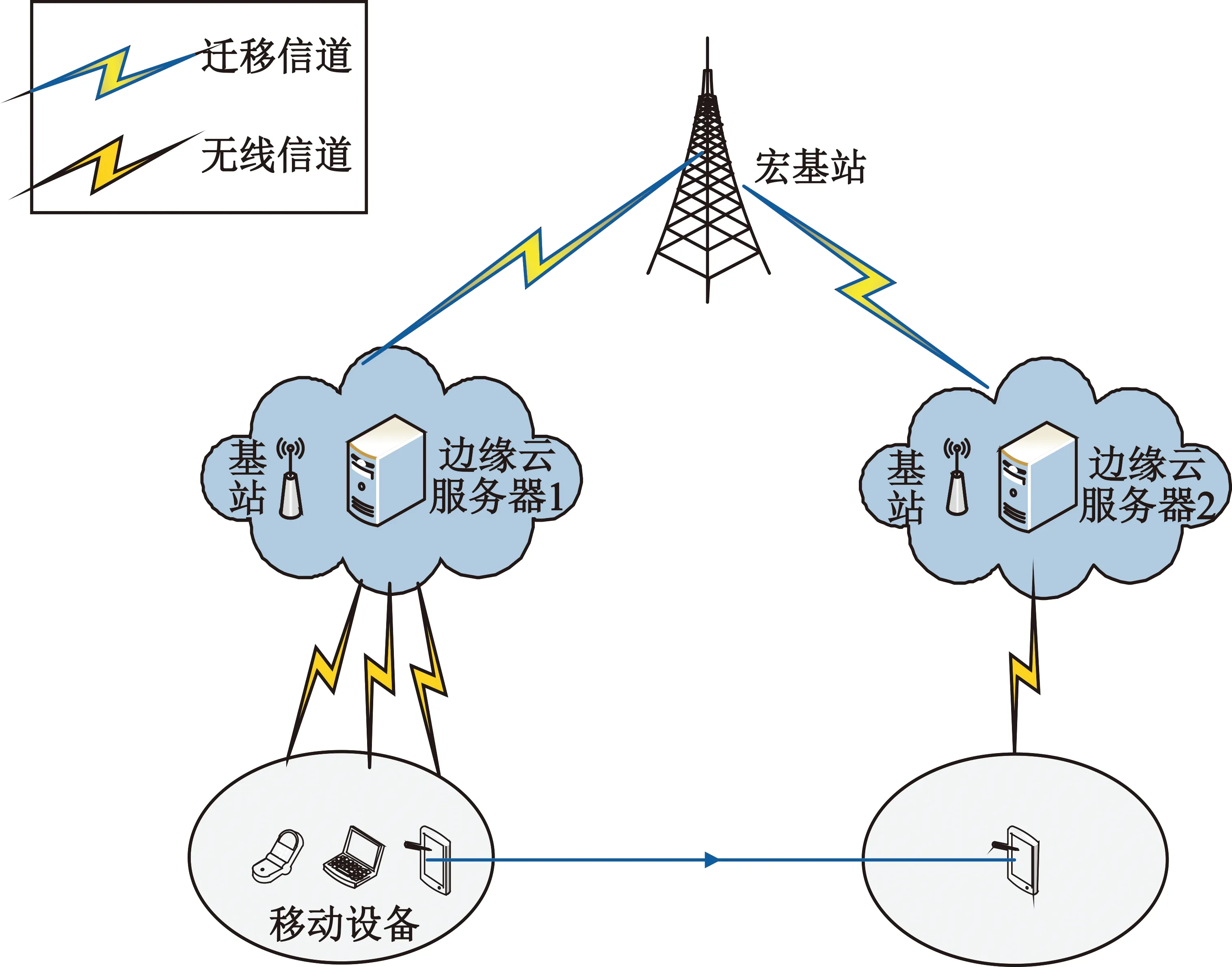
图1 基于迁移的系统模型

1.2 计算模型
(1)本地计算模型
假设移动设备的计算能力为Fl,则任务i在本地的计算时间可表示为
(1)
参考文献[6],计算消耗是计算能力的超线性函数,表示为:pl=κl(Fl)γ,其中γ=2,κl表示CPU的有效电容系数[6],设置为10-15。
任务i在本地的计算能耗可计算为
(2)
(2)传输计算模型
移动设备通过无线信道将计算任务卸载到边缘节点,总消耗时间包括传输时间以及云上执行时间两部分[6],其传输速率可表示为
(3)
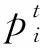
(4)
(5)
(3)边缘云计算模型

(6)
(7)
式中:κe表示CPU的有效电容系数,设置为10-16来满足边缘云计算的能耗需求。
1.3 迁移模型
由于移动设备不是静止不动的,本文定义任务停留时间t为任务在边缘云服务范围内所待时间,若任务在边缘云上执行时间大于任务停留时间,则任务需要在两个边缘云内进行迁移,否则无需迁移。采用停留时间的概率密度函数来体现移动设备的移动性[3-5],表示为
(8)
式中:wi表示任务i的平均停留时间[3]。
2 卸载模型以及优化问题
2.1 卸载模型
本文将卸载过程建立为马尔科夫决策过程(Markov Decision Process,MDP)。MDP是时序决策的标准方法,可以在计算资源充足的条件下给出最优解。MDP考虑了动作及系统的下个状态不仅和当前的状态有关还和采取的动作有关,其中比较重要的三个元素为状态S、动作A以及回报R。
(1)状态S
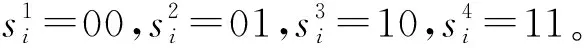
S={S0,S1,S2,…,SN-1,ST} 。
(9)
(2)动作A
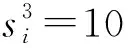

图2 状态转变图
(3)回报R
回报也被称为奖励函数,即任务执行完动作后会得到某个状态下的奖励,一般作为决策的依据。通常回报函数和目标函数相关。由于MDP追求最大化回报,本文的优化目标是最小化损耗函数之和,因此回报函数与之存在负相关关系。
2.2 优化问题
本文定义损耗函数(Loss Function,LF)来衡量服务用户质量,将卸载问题转化为在一定约束条件下损耗函数之和最小化的问题。其中损耗函数定义为特定状态下时间和能耗与全部在本地执行比值的加权和。损耗函数表示为
(10)
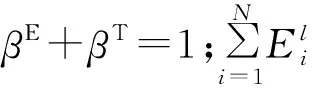
即前一个任务和当前任务均在本地执行,仅需考虑任务i在本地执行的能耗以及时延,表示为
(11)
(12)
因此该状态下损耗函数表示为
(13)
即前一个任务在本地执行,当前任务在边缘云执行,需要考虑传输数据以及移动设备的移动性。根据任务停留时间t和该状态下任务在边缘云系统中完成计算的时间T1的长度关系分情况讨论:
①t>T1,即任务可以顺利地在边缘云1上完成卸载不会发生迁移,这种情况的概率记为Pwi(t>T1)。
(14)
用FTi-1表示前一个任务的完成时间,根据图2可以看出完成时间依赖于状态00或者10,引入p00、p10来表示来自这两状态的概率。即
(15)

(16)
②t≤T1,即任务不能顺利在边缘云1完成,需要迁移至边缘云2完成,这种情况的概率记为Pwi(t≤T1)。由于发生迁移额外产生了迁移成本,用Em=ηHi表示,其中η表示单位迁移价格,此时能耗为
(17)
根据移动模型(8),可以计算得到相应的概率为
(18)
P2=Pwi(t>T1)=1-Pwi(t≤T1)。
(19)
因此该状态下能耗公式可整合为
(20)
时延为
(21)
此状态下损耗函数表示为
(22)
即前一个任务在边缘云系统中执行,当前任务在本地执行,则此状态的能耗和时延表达式为
(23)
(24)
因此该状态下的损耗函数为
(25)
即前一个任务和当前任务均在边缘云系统中执行,但要考虑的是当前任务是在边缘云1还是边缘云2执行,因此仍要分情况考虑:
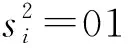
(26)
引入p01、p11来表示来自这两状态的概率:
(27)

(28)
②t≤T2,该情况的概率记为Pwi(t≤T2),类比于状态01,此时能耗为
(29)
(30)
P4=Pwi(t>T2)=1-Pwi(t≤T2)。
(31)
该状态下的能耗和时延表示为
(32)
(33)
因此该状态下的损耗函数表示为
(34)
本文需要按顺序依次对所有任务进行状态决策,目标是通过优化传输功率以及进行卸载决策使得损耗函数之和最小,将优化问题可描述为
(35a)
s.t.
(35b)
(35c)
(35d)
(35e)
式中:C1约束是对传输功率的限制;C2约束是保证边缘云的频率不超过服务器的最大频率;C3约束表示的是每一状态的计算时间要小于任务完成的最大时延;C4约束表示的是每个任务选择的子状态空间的任何状态要在整个系统状态范围内,即任务可选择在本地执行或者在边缘云系统中执行。
3 问题求解
3.1 资源分配问题
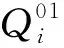
(36a)
s.t.
(36b)
对公式进行化简,即
(37)

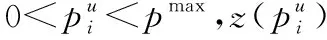

ifz(pmax)≤0 then
else
repeat
else
end if
end if
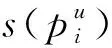
(38)

(39)
3.2 基于Q-learning的卸载算法
本文提出QLBA(Q-learning Based Algorithm)来实现卸载决策。Q-learning算法思想:通过状态和动作构建一个Q值表,根据Q值来选取获得最大回报的动作[7-8]。该算法核心是以一个episode为一个训练周期,采用时序差分法更新Q值表,公式为
Q(s,a)=(1-α)Q(s,a)+α[R+γmaxQ(s′,a′)]。
(40)
式中:γ越趋近于0表示更注重眼前的奖励;γ越趋近于1表示更注重未来的奖励;α表示学习率为Q值和当前Q值的比率,若α越趋近于1表示保留之前的值越少。Q-learning的优势就是融合了蒙特卡洛以及动态规划进行离线学习,通过求解贝尔曼方程得出最优路径。本文的优化目标是最小化损耗函数之和,因此回报函数与之存在负相关关系,即问题(35)转换为
(41)
(42)
QLBA算法如下:
设置初值以及矩阵R,初始化矩阵Q全为0。
对于每一个episode:
(1)随机选择一个初始状态;
(2)在当前状态的所有可能行为中选取一个动作;
(3)利用选定的动作a得到下一个状态;
(4)根据式(40)计算Q值;
(5)直到达到最终目标状态停止。
3.3 算法复杂度
由文献[6]可知,资源分配阶段采用的二分法的复杂度为O(lb(p/ε)),卸载决策阶段采用的Q-learning算法的复杂度为O(N2),因此算法总体复杂度为O(lb(p/ε))+O(N2)。
4 仿真结果及数据分析
此部分对所提算法进行评价,采用Matlab进行仿真,与其他三种不同的方案进行比较,即完全卸载方案(All-edge scheme)、本地计算方案(All-local scheme)和文献[9]中随机卸载方案(Random scheme)。本文假设边缘云的覆盖半径为500 m,移动设备和边缘云之间的无线信道增益遵从瑞利随机衰落。其他仿真参数参考文献[6]和[10]设置,如表1所示。
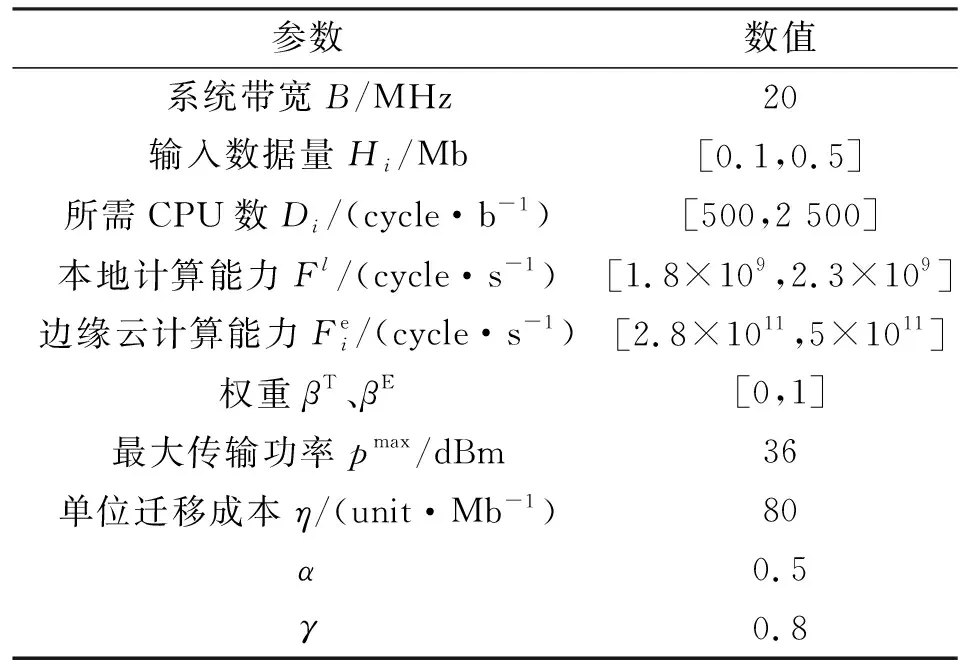
表1 仿真参数
首先将任务数设置为25,βE、βT分别设置为0.6、0.4。图3给出了Q-learning的学习收敛曲线,可以看出经过1 000次迭代,损耗函数趋于一个稳定的值,证明了本文提出的QLBA算法是收敛的。
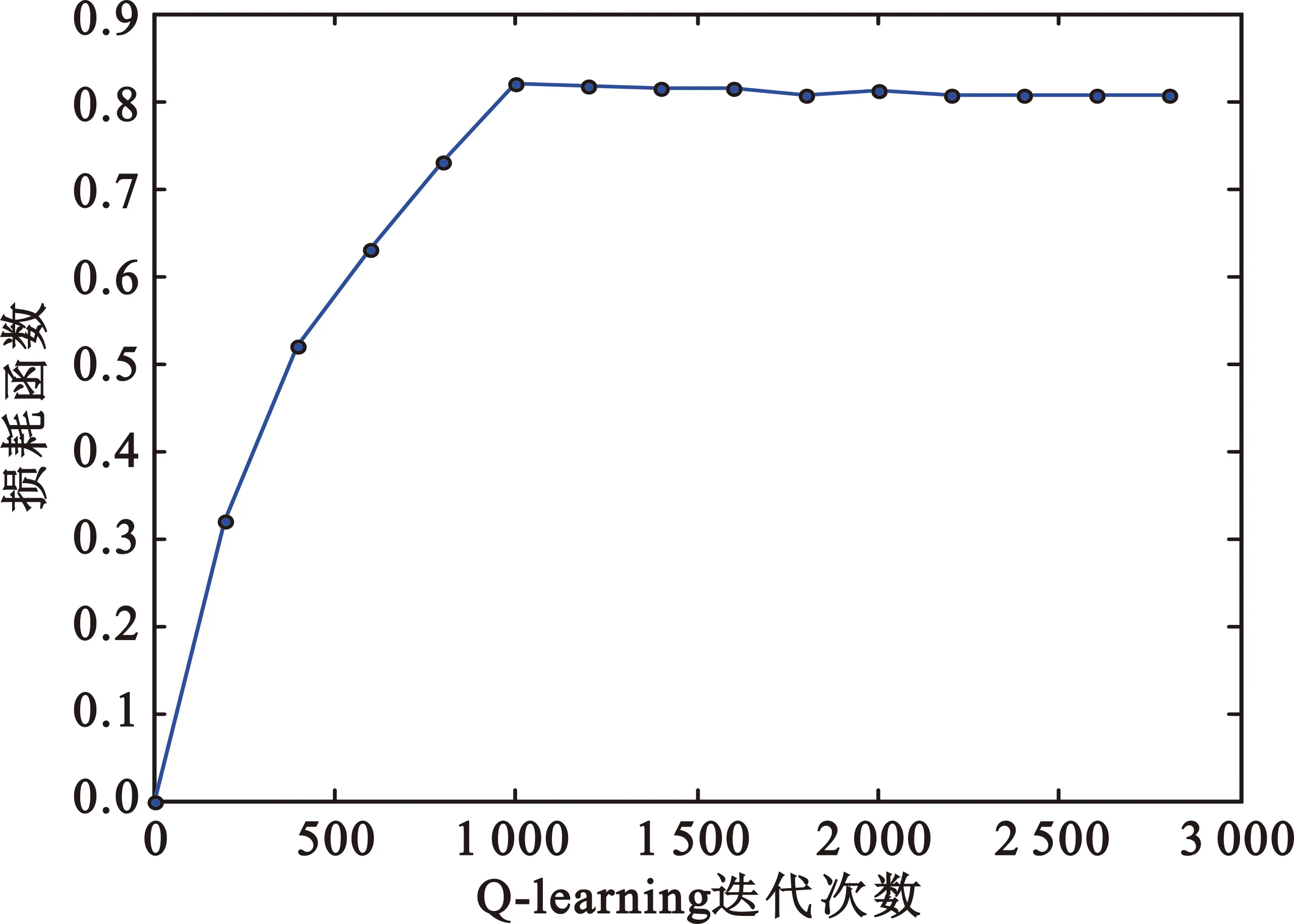
图3 Q-learning学习收敛曲线
不同任务数下(任务数25~55)四种方案的损耗函数对比如图4所示。假设每个任务的数据量和计算能力不同,仿真时在给定范围随机取值,服从均匀分布;βE、βT分别设置为0.6、0.4。本文以All-local scheme作为对比基准,该方案始终为1,其他三种方案由于受无线信道状态以及计算资源的限制都有所波动,可看出在不同任务数下本文所提出的QLBA优于其他三种方案,可以从总体上最小化损耗函数。

图4 不同应用的任务数的损耗函数
然后讨论权重βE、βT对损耗函数的影响。本文方案与其他三种方案的βE与损耗函数的关系如图5所示,此时任务数设置为25,仍以All-local scheme作为基准。可看出当βE小于0.48时,全部在边缘云系统执行和所提方案几乎无差别,但都优于文献[9]中的随机方案;当βE大于0.48后,任务全部卸载方案的损耗函数增加得较快,可见完全卸载比较适用于对延迟比较敏感的应用。而本文提出的方案增长比较平稳,在这几种方案中最优,证明了QLBA的优越性。随着βE的增加,可看出QLBA逼近全本地方案,可得出对延迟不敏感的应用更倾向在本地执行任务。

图5 βE与损耗函数的关系
图6和图7分别给出了随着βE的增加四个方案的能耗以及时延的变化趋势。

图6 βE与能耗关系图

图7 βE与时延关系图
从图6可看出All-local scheme的能耗最小,All-edge scheme的能耗最大。原因有以下几点:一是All-local scheme相对于其他三种方案节省了传输能耗;二是本地的计算能力相对于在边缘云的计算能力要小;三是对于全部在边缘云上执行的任务来说,由于边缘云计算资源有限,发生迁移的概率较大,导致能耗比其他方案高。
从图7可看出任务全部在本地执行的时延最高,全部卸载方案的时延最低。随着βE的增加,QLBA的时延逐渐增加,逐渐和All-local scheme逼近。由此可得出结论:对时延比较敏感的应用分配较小的βE,对能耗比较敏感的应用分配较大的βE。综上可得出,本文所提出的方案可以从总体上使系统损耗最小。
5 结束语
由于数据传输过程中的任务迁移导致额外的迁移成本,为降低迁移概率以及最小化损耗函数之和,本文提出了基于迁移的移动边缘云系统的资源分配以及任务卸载。首先将应用卸载过程建模为MDP,考虑时延和能耗对决策的影响,定义损耗函数来衡量用户质量,将问题转化为最小化损耗函数之和。先采用二分法在任务卸载前对每个任务的传输功率进行优化,再采用QLBA对任务进行决策。仿真结果表明本文提出的方案优于其他三种方案。未来工作中将进一步考虑多用户的数据迁移问题。

