一种全空域球面相控阵天线对非协同目标的过顶跟踪方法*
扈景召,王文政,杜 丹,官 劲,魏瑞利
(1.中国西南电子技术研究所,成都 610036;2.西安卫星测控中心,西安 710043)
0 引 言
相位阵列天线是基于可以控制的阵列天线,通过改变天线波的相位来改变天线波束指向,所以称作“相控阵”[1]。相控阵天线可同时形成多个波束,每个波束的指向角度变换极为快速,单个波束指向响应时间可达到毫秒量级,且可看作是无惯性的。因此相控阵天线具有波束响应时间短、多目标跟踪、边搜索边跟踪等优点[2]。另外,相控阵天线可采用球面阵列设计,实现全空域覆盖,具有很强的工作灵活性和自适应能力,方便建设大型天线,在航天及航空测控领域有广阔的应用前景[2]。
球面相控阵天线在工程化过程中,一个需解决的关键技术问题是对目标的高仰角过顶跟踪问题:球面相控阵天线与传统抛物面天线一样,同样采用方位、俯仰角的自跟踪方式,在待跟踪目标相对于天线以较大的俯仰角过顶时,与传统天线类似,球面相控阵天线同样会出现天线自跟踪系统的方位与俯仰角动态过大问题。尤其当被跟踪目标以90°仰角对天线过顶时,天线跟踪的方位角轨迹会发生180°突变,最终会导致球面阵天线自跟踪系统无法对目标进行连续跟踪[3]。传统机械天线系统中,天线的坐标系在天线的安装时就固定了,无法动态旋转,因此只能通过程序引导或者旋转第三轴等辅助办法来降低目标过顶时对天线自跟踪系统的影响,而无法从根本上解决目标过顶的自跟踪问题[4]。
文献[3]和[5]都对球面相控阵天线过顶跟踪问题进行了分析。文献[3]讨论了一种球面相控阵天线应用于航天测控领域的对协同目标的过顶跟踪方式,但是对于非协同目标,由于无法预测被跟踪目标的过顶点,因此文献[3]给出的过顶跟踪解决方案并不适用。文献[5]给出了一种折中的球面相控阵天线过顶跟踪的解决方案,该方案适用于对非协同目标的过顶跟踪,但该过顶跟踪解决方案有两点缺陷:一是在对目标高仰角过顶跟踪时存在跟踪的稳态误差,只能保证波控角跟踪环路不丢失目标;二是在高仰角跟踪目标时应用该折中方案会出现差波束的畸变,从而导致角跟踪精度的降低[5]。
本文针对球面相控阵天线的特点,提出了一种球面相控阵天线对非协同目标的过顶跟踪方法,在航天与航空测控领域都能有效解决球面相控阵天线对目标的过顶跟踪问题。
1 球面相控阵天线对非协同目标角跟踪的过顶方法
1.1 基本思路
本文提出的对非协同目标过顶自跟踪方案的基本思路为:首先在当前捕获目标位置估算目标运动轨迹,然后根据估算偏转角对球面阵天线跟踪坐标系进行旋转,如图1所示。旋转后形成新的坐标系,在新的坐标系中,xoy平面与目标轨迹基本在同一平面上,因此在该坐标系下目标运动轨迹始终是处于低仰角状态,天线跟踪能保证跟踪精度及不出现过顶问题。

图1 全空域球面相控阵天线过顶跟踪示意图
1.2 对非协同目标的过顶自跟踪流程
全空域球面相控阵天线的对非协同目标角跟踪流程如图2所示,跟踪流程包括两个阶段:第一个阶段是完成对目标的捕获,并在传统坐标系下对目标的自跟踪;第二个阶段是捕获目标后判定目标轨迹方向,再进行坐标旋转,即在稳定的自跟踪过程中计算出过顶跟踪旋转角,再通过过顶跟踪旋向角计算坐标系旋转矢量,最后将波束对目标的自跟踪切换到旋转后的坐标系下完成对非协同目标的过顶跟踪处理流程。其中坐标旋转矢量A1的计算与目标指向有关,坐标旋转矢量A2的计算与过顶跟踪旋转角有关。

图2 角跟踪系统示意图
1.3 对非协同目标的过顶自跟踪算法
1.3.1 坐标系旋转矢量A1的计算
A1表示为
(1)
式中:φ为目标指向的俯仰角,φ为目标指向的方位角。
在全空域球面相控阵天线中,也可采用传统抛物面天线所采用的单脉冲跟踪体制或者圆锥扫描角跟踪体制。由于全空域球面相控阵天线采用数字波束形成,因此在实现上与传统抛物面天线还是有所区别的。
1.3.2 波控角跟踪环路设计
对于如何在相控阵天线中如何设计数字角跟踪环路在文献[6]中已经进行了详细分析,这里引用其结论。
图2角跟踪系统的数字域实现如图3所示。

图3 角跟踪环路数字域实现模型
波控数字角跟踪环路计算公式如下:
(2)
式中:G1、G2、K0为常量系数,θA/E(n)为当前目标方位/俯仰角,θA/E(n-1)为上一轮计算所得目标方位/俯仰角,VA/E(n)为当前上报方位/俯仰误差电压。
值得注意的是,这里波控跟踪环路是建立在过顶跟踪处理后的新坐标系下,跟踪环路得到的目标指向的方位角与俯仰角也是在新坐标系下的。要得到原坐标系下目标指向的方位与俯仰角,需要用坐标系旋转矢量进行转换。xA/E(n)、yA/E(n)为方位/俯仰环路计算的中间变量,跟踪开始时初始化。
1.3.3 过顶跟踪旋转角的计算
过顶跟踪旋转角计算如下:
ψ=arctan(Δφ/Δφ)。
(3)
式中:Δφ=θE(n)-θE(n-1)为当前目标的俯仰角变化率θE(n),见公式(2);Δφ=θA(n)-θA(n-1)为当前目标的方位角变化率,θA(n)见公式(2)。
1.3.4 坐标系旋转矢量A2的计算
A2表示为
(4)
式中:ψ为公式(3)计算的过顶跟踪旋转角。
1.3.5 差阵列划分策略
在新坐标系下,计算球面天线各个阵元的坐标(极坐标),按照目标在新坐标系下坐标划分方位与俯仰差阵列,步骤如下:
(1)设目标在新坐标系下位置方位角为θA,俯仰角为θE,计算各个阵元在新坐标系下的位置:

(5)
式中:x1、y1、z1为子阵在原坐标系下的坐标,A1与A2取值分别如公式(1)和公式(4)所示。
(6)
(2)方位差阵列按如下策略划分:θA≤θA阵元<θA+90° 内的阵元取为方位差阵列正值;θA<θA阵元<θA-90° 内的阵元取为方位差阵列负值。
(3)俯仰差阵列按如下策略划分:θE≤θE阵元<θE+90° 内的阵元取为俯仰差阵列正值;θE≤θE阵元<θE-90° 内的阵元取为俯仰差阵列负值。
2 对非协同目标过顶自跟踪的算法仿真
与文献[3]一样,本文仿真设定飞行器轨道高度为300 km。需要注意的是,对非协同目标过顶自跟踪仿真必须考虑在不同仰角条件下进行防过顶算法处理的仿真。
仿真实验条件:目标轨道高度为300 km,目标飞行速度为7.75 km/s,地球半径为6.378 14×103km,目标过顶仰角(基于传统坐标系)分别为90°、83°、40°、15°。仿真结果如图4~7所示。

图4 83°仰角过顶时传统坐标系及防过顶处理后卫星角跟踪情况比较
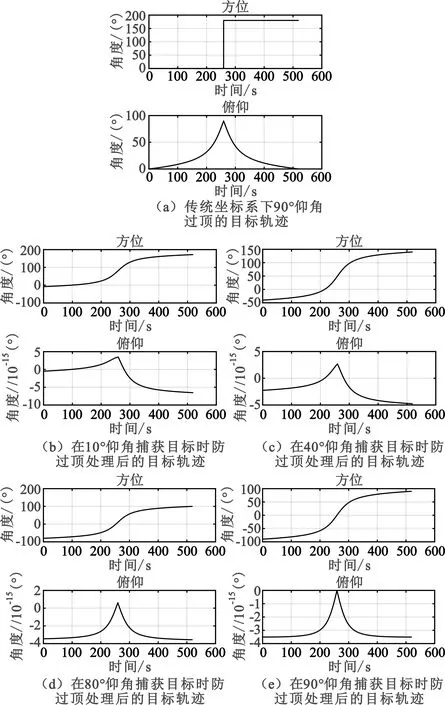
图5 90°仰角过顶时传统坐标系及防过顶处理后卫星角跟踪情况比较
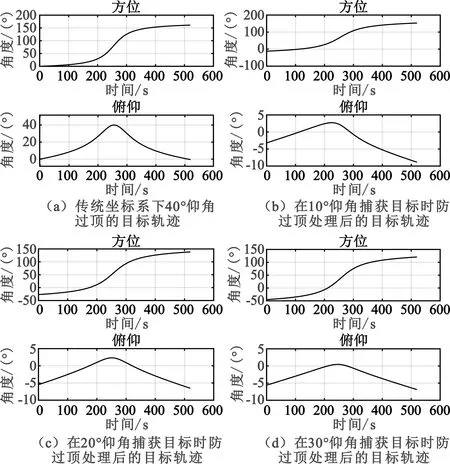
图6 40°仰角过顶时传统坐标系及防过顶处理后卫星角跟踪情况比较

图7 15°仰角过顶时传统坐标系及防过顶处理后卫星角跟踪情况比较
以图4对非协同目标在传统坐标系下83°仰角过顶的仿真结果为例,在目标分别处于10°、40°、70°仰角时捕获目标并进行防过顶算法处理,结果表明在做了防过顶算法处理后的新的坐标系下,目标的仰角变化范围为0.7°~-1.5°。整个仿真结果统计如表1所示。

表1 对非协同目标防过顶跟踪算法仿真结果(卫星高度300 km)
根据表1统计的仿真结果可知,采用本文方案,球面相控阵天线在任意目标可视弧段内捕获非协同目标后,都能确保该目标相对应球面阵跟踪坐标系始终处于低仰角状态。根据文献[3]的分析结论,本文方案可有效减少目标过顶时角跟踪的速度与加速度,在各个不同的目标仰角过顶条件下的最大角速度≤1.5°/s,最大角加速度≤0.023 6°/s,有效避免了跟踪时由于角速度或角加速度过大导致的对目标跟踪不稳定甚至丢失目标的情况[3]。并且,由于本文方案的低仰角跟踪目标的特点,可采用1.3.5节中的差阵列划分方法,有效地简化了工程实现的算法难度。
由以上仿真结果还可以看出,对于飞行高度大于300 km的空间目标,只进行一次计算过顶跟踪旋转矢量A2及坐标系旋转处理就能解决球面相控阵天线过顶跟踪问题;对于飞行高度小于300 km的空间目标,可在本文方案的基础上采用多次迭代旋转的方式,即可设定跟踪俯仰角门限为±10°,在对目标进行跟踪过程中当俯仰跟踪角超过跟踪门限时,重复1.3.3~1.3.5节的过顶跟踪坐标系旋转处理流程。
3 结 论
本文针对非协同目标提出了一种解决全空域球面相控阵天线过顶跟踪问题的方法,并对低轨航天目标在不同仰角过顶条件下应用该方法进行了动态仿真。仿真结果表明,应用该方法可使得球面阵天线的跟踪系统在整个对目标的自跟踪过程中保持低仰角跟踪状态,这样可减小天线对目标的角跟踪动态,避免出现天线丢失目标的情况。进一步分析表明,本文提出的过顶跟踪方法不仅适用于飞行高度较高的航天飞行器目标的过顶跟踪,且同样适用于对飞行高度较低的航空飞行器的过顶跟踪,因而本文所提方法可以很好地解决球面相控阵天线对非协同的飞行目标的自跟踪需求,有着广泛的应用前景。

