考虑磁差的鲁棒DME/VOR/SINS组合导航算法*
方 涛
(中国西南电子技术研究所,成都 610036)
0 引 言
全球导航卫星系统(Global Navigation Satellite System,GNSS)、捷联惯导系统(Strapdown Inertial Navigation System,SINS)、测距仪(Distance Measuring Equipment,DME)和伏尔(Very High Frequency Omnidirectional Range,VOR)是民航基于性能的导航中常用的导航系统[1-2]。其中,GNSS因具有导航精度高、全天候和全球性的特点,成为最常用的导航系统。然而GNSS信号在高动态情况下信号抗干扰处理复杂使得飞行管理系统研发者在设计系统时必须考虑配置有效的导航备份[3-4]。DME/VOR/SINS的组合导航方式中,由于DME和VOR同址安装且具有信号覆盖范围广的优点,应用场景更广,值得深入研究。
目前国内民航客机应用广泛的进口飞行管理系统中,导航算法封装于系统内部,无法得知其具体实现细节,且相关文献报道较少。国内针对VOR/DME/SINS组合导航系统开展了部分理论研究:文献[5]采用联邦卡尔曼滤波器设计了机载多传感器组合导航系统,并在其子滤波器中设计了塔康(Tactical Air Navigation,TACAN)/SINS组合导航系统(TACAN可看作VOR/DME同址安装在军用领域的应用,两者输出完全相同);文献[6]采用联邦卡尔曼滤波器设计了SINS/GNSS/TACAN组合导航系统,在组合导航的同时实现动态校正、对准和标定;文献[7]设计了基本的TACAN/SINS组合导航算法;文献[8]推导了系数加权的联邦卡尔曼滤波算法,并将该算法应用于SINS/GNSS/TACAN组合导航算法中;文献[9]设计了机载导航系统的故障检测与处理算法;文献[10]同样采用联邦卡尔曼滤波器设计了大飞机综合导航算法,其导航系统包括SINS、GNSS、DME、VOR和星敏感器;文献[11]针对SINS/大气数据机/GNSS/TACAN/雷达综合导航系统,对比分析了两类联邦滤波系统级的故障检测方案。上述针对DME/VOR/SINS组合导航的研究仅停留在理论层面,并未考虑实际应用中存在的问题:一是上述研究均假设TACAN或VOR输出的方位测量基准为真北,而实质上两者输出的方位测量基准为磁北,后文的测试结果将会看到磁差(地理北与磁北的角度差值)对组合导航系统有较大的影响;二是当飞机在VOR台站上空附近飞行时VOR输出的方位信息含较多的野值,野值对组合导航系统的精度也将产生消极影响。
本文针对上述两个实际问题,提出了一种考虑磁差的鲁棒DME/VOR/SINS组合导航算法。实验测试结果表明,考虑磁差的组合导航算法显著提高了系统的导航精度,同时由于采用了鲁棒的卡尔曼滤波算法实现信息融合,算法的鲁棒性得到了有效提升。
1 问题描述
1.1 磁方位与真方位
伏尔系统是一种由机载设备直接输出导航参量的近程无线电导航测角系统,导出的导航参量是飞机相对于伏尔信标台的磁方位角,磁方位和真方位的关系如图1所示。
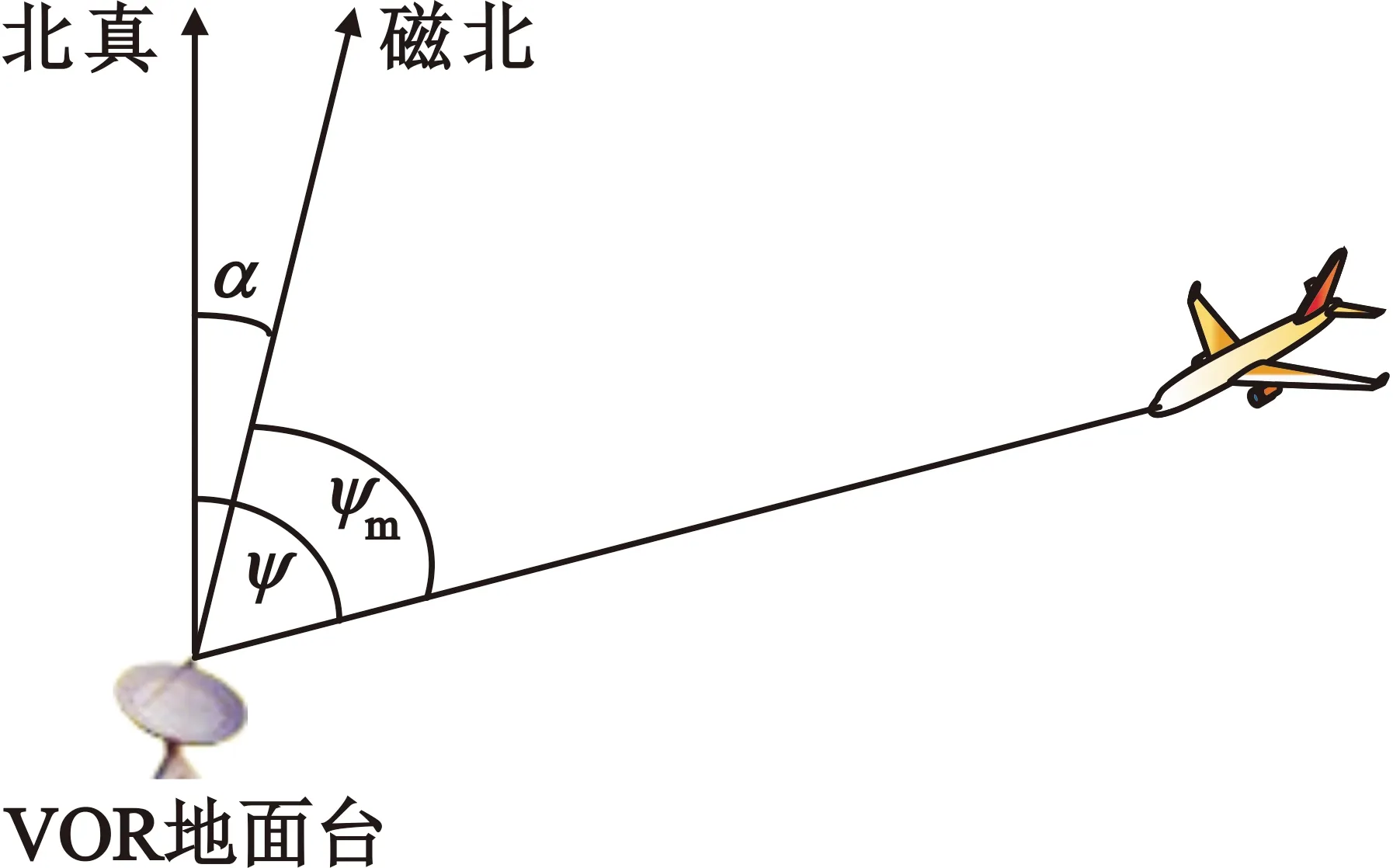
图1 磁方位和真方位关系示意
图1中,α=ψ-ψm,ψ为真方位,ψm为磁方位,α为磁差。一般情况下,磁差随纬度变化,纬度越高,磁差越大。以我国为例,最北端漠河镇的磁差大约为11°。显然,在忽略磁差的情况下,假设VOR输出的方位测量值参考为真北,组合导航系统的导航精度将受到严重影响,第4节将重点对比忽略磁差和考虑磁差两种情况下组合导航系统的精度。
1.2 方位测量野值对组合导航的影响
VOR方位测量输出野值的原因为相控阵天线在±60°的顶空盲区附近增益下降明显,使普通幅度调制度降低,产生的15 Hz、135 Hz相位发生形变,导致方位输出发生跳变。某次实际飞行测试过程中VOR方位测量噪声如图2所示,当飞机飞行至台站上空附近时,VOR输出方位在4 500 s的时间内产生多次跳变。显然,方位测量中的野值将对组合导航系统的鲁棒性产生重要影响,在滤波稳定性受到严重影响时,其导航输出结果甚至不可靠。第4节将测试和分析方位测量野值对组合导航系统的影响。
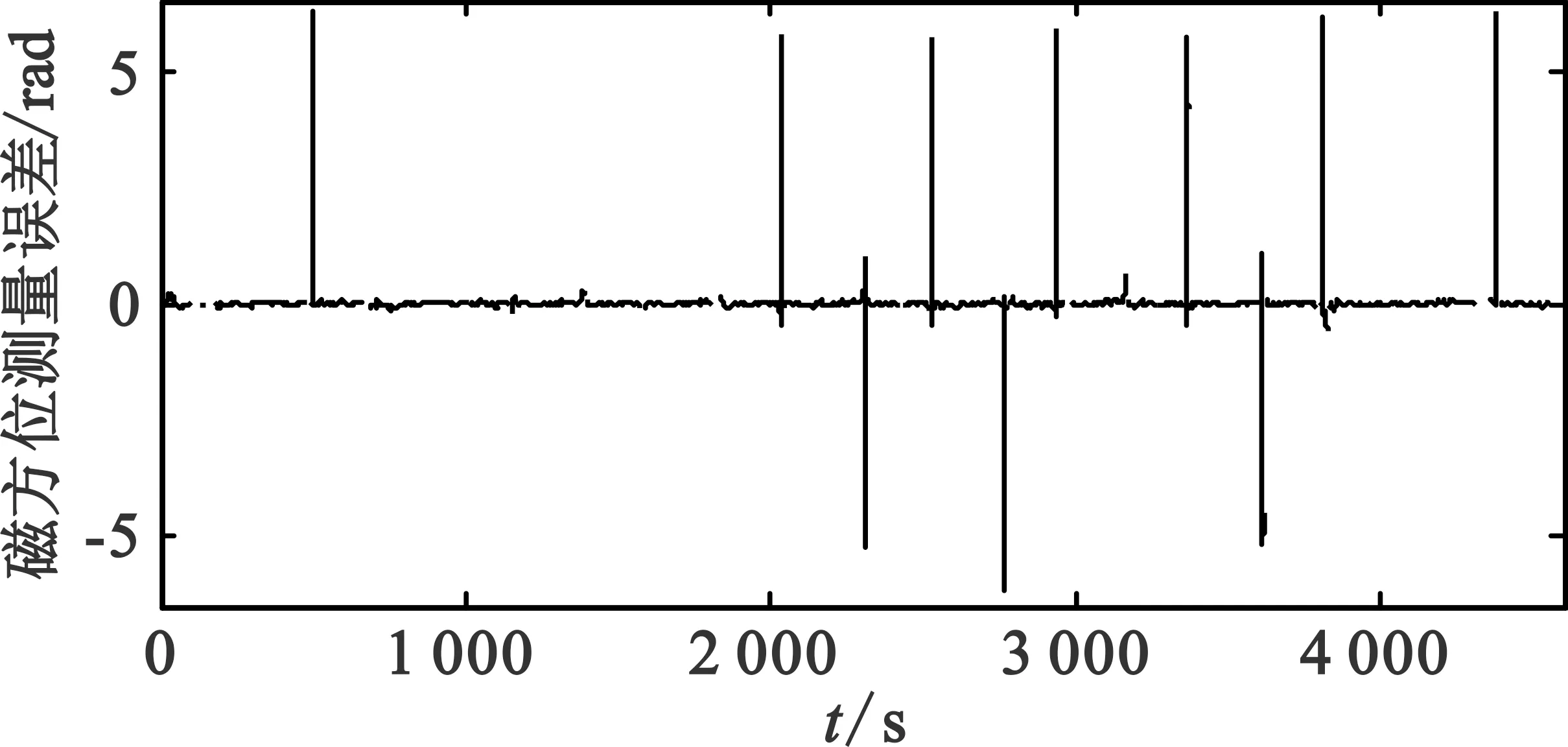
图2 VOR台站上空附近磁方位输出
2 DME/VOR/SINS组合导航系统设计
2.1 算法实现方案
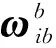
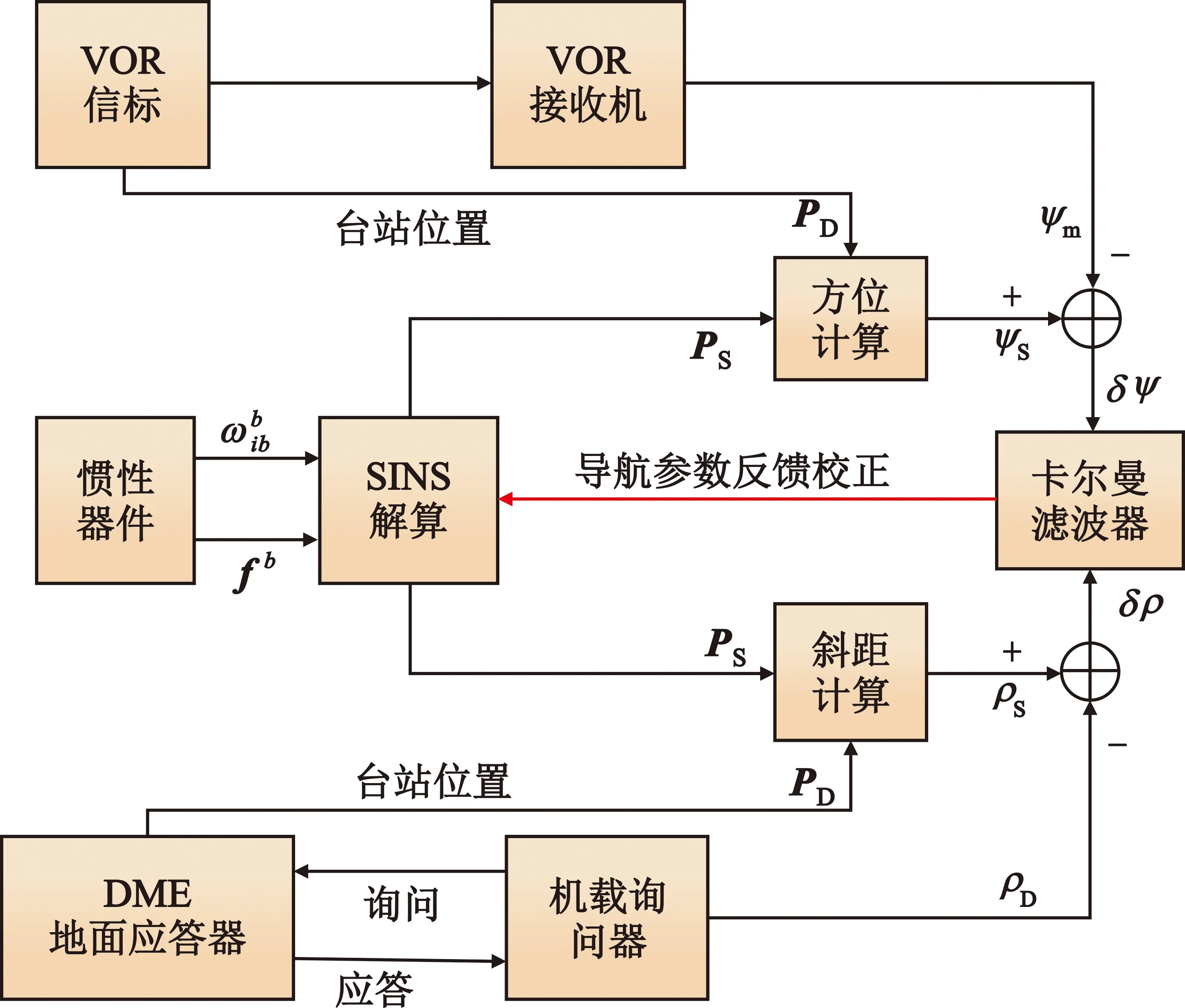
图3 DME/VOR/SINS组合导航系统
2.2 组合导航状态方程
本文以机载SINS误差传播方程为基础,建立DME/VOR/SINS组合导航卡尔曼滤波的状态方程,状态变量X包括三轴姿态误差φx、φy和φz;东北天方向的速度误差δVE、δVN和δVU;经度、纬度和高度误差δλ、δL和δh;三轴陀螺常值漂移εcx、εcy和εcz;三轴加速度计常值零偏▽cx、▽cy和▽cz。
区别于已有的研究,本文不再假设VOR输出的方位为真方位,将台站的磁差纳入参数估计的范畴。考虑到某一固定位置的磁差在相当长的时间内不会发生大的变化,将台站磁差α假定为常值:
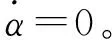
(1)
在SINS误差方程的基础上[12],考虑式(1),组合导航卡尔曼滤波的状态方程如下:
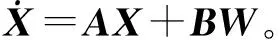
(2)
式中:矩阵A和B可参考文献[12]并结合式(1)得到;系统噪声序列
εrx、εry和εrz为三轴陀螺随机漂移,▽rx、▽ry和▽rz为三轴加速度计随机零偏,ζ为磁差随机误差,近似为高斯白噪声。
2.3 组合导航量测方程

(3)
(4)
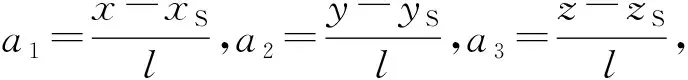
lU=l+a1δx+a2δy+a3δz。
(5)
DME输出的斜距可表示为
lS=l+υ。
(6)
式中:υ为DME斜距测量噪声。
根据式(5)和式(6),斜距差量测方程可表示为
δl=a1δx+a2δy+a3δz-υ。
(7)
SINS误差方程中选择的位置误差变量为δλ、δL和δh,因而需要将式(7)中的位置误差δx、δy和δz转换为δλ、δL和δh。文献[13]给出了上述两类位置误差的转换关系:
(8)
式中:RN为地球卯酉圈半径。
结合式(8),式(7)可进一步表示为
δl=b1δλ+b2δL+b3δh-υ。
(9)
式中:b1、b2和b3的具体形式分别为
考虑台站磁差α,结合文献[8]给出的方位测量误差的表达式,方位测量误差表达式为
(10)
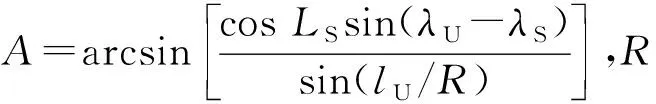
结合式(9)和式(10),卡尔曼滤波的量测方程为
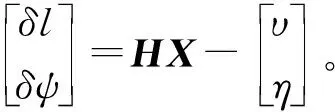
(11)
式中:量测矩阵H的具体形式为
3 基于M估计的卡尔曼滤波算法
经典的卡尔曼滤波在噪声统计特性符合高斯分布时具有状态变量的最优估计,然而,实际应用中噪声特性不可能完全符合高斯分布,在噪声严重偏离高斯分布时状态估计甚至会出现错误。在DME/VOR/SINS组合导航应用中,如1.2节所述,VOR方位测量会出现野值,若采用经典卡尔曼滤波实现信息融合,状态估计的性能将受到影响。本文采用在工程应用中具备良好抗野值能力的基于M估计的卡尔曼滤波(M-estimation Based Kalman Filter,MKF)算法实现信息融合。根据式(2)和式(11),k时刻离散化后的组合导航状态方程和量测方程为
式中:Φk,k-1为离散化后的状态转移矩阵,Γk-1为离散化的系统噪声驱动阵,Zk为量测,Vk为量测噪声序列。
滤波算法采用的L1范数和L2范数混合的代价函数为
(12)
式中:τi为矩阵τ的第i个元素,κ为调节因子。
定义矩阵
(13)
则矩阵ψ对角线上的第i个元素ψi可表示为
(14)
MKF算法执行流程如下:
Step1 设置状态变量初值X0、估计均方误差阵P0、系统噪声方差阵初值Q0、量测噪声方差阵R0、迭代次数N、调节因子κ、k=1。
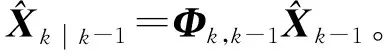
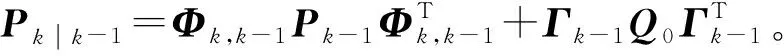
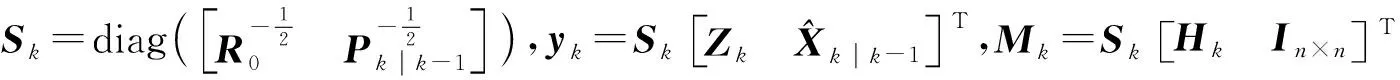
Step5 计算τ=MkXk-yk。
Step6 结合式(12)、(13)和(14)计算矩阵ψ。
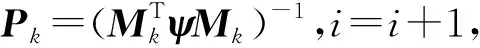
4 实验与分析
4.1 实验测试条件
以某次飞行中记录的机载SINS惯性器件输出为基础,对本文所设计的DME/VOR/SINS组合导航算法进行测试,惯性器件输出频率为100 Hz。以机载SINS/GNSS组合导航系统输出的导航参数为参考,对导航算法的定位精度进行定量分析。SINS解算采用最常用的指北方位惯导力学编排,该力学编排适用于除极区以外的绝大多数区域。飞机在水平方向上的相对运动轨迹如图4所示。
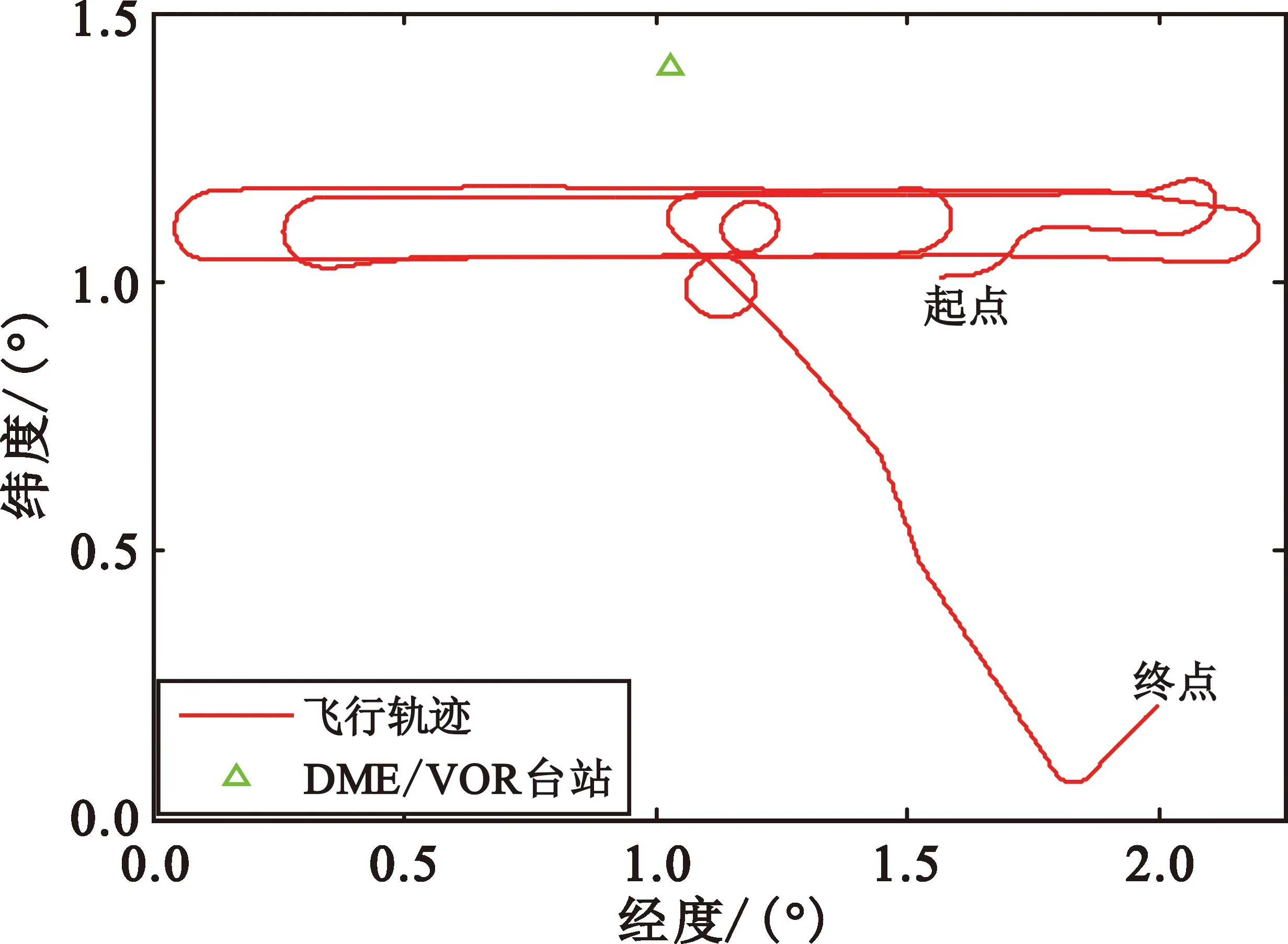
图4 水平面内的相对飞行轨迹
图4中,DME/VOR台站同址安装,其位置根据飞机运动轨迹设置得到,纬度1.4°,经度1.03°,高度0 m。为确保算法验证的有效性,本文采取半物理仿真的策略模拟DME和VOR的输出,即采用在DME和VOR输出的理论真值中叠加实际测量噪声的方法模拟图4台站位置处的DME和VOR的输出。DME和VOR的输出频率为20 Hz,输出的理论真值根据台站位置与飞机位置参考计算得到。本文重点测试飞机飞行至VOR台站上空时VOR输出的磁方位信息包含野值的情况,VOR的实际测量噪声如图2所示。
4.2 实验测试结果及分析
4.2.1 磁差对组合导航系统影响测试
首先测试组合导航系统考虑磁差和不考虑磁差的两种情况下组合导航系统的性能。设VOR台站的磁差为-5°,两种测试中均采用基于M估计的卡尔曼滤波实现信息融合。算法测试过程中,为保证迭代收敛,滤波迭代次数N设置为10,调节因子κ设置为经典参数1.345。考虑磁差的情况下,磁差的估计结果如图5所示。

图5 磁差估计值
两种测试方案下组合导航系统的姿态误差、速度误差和位置误差如图6~8所示。
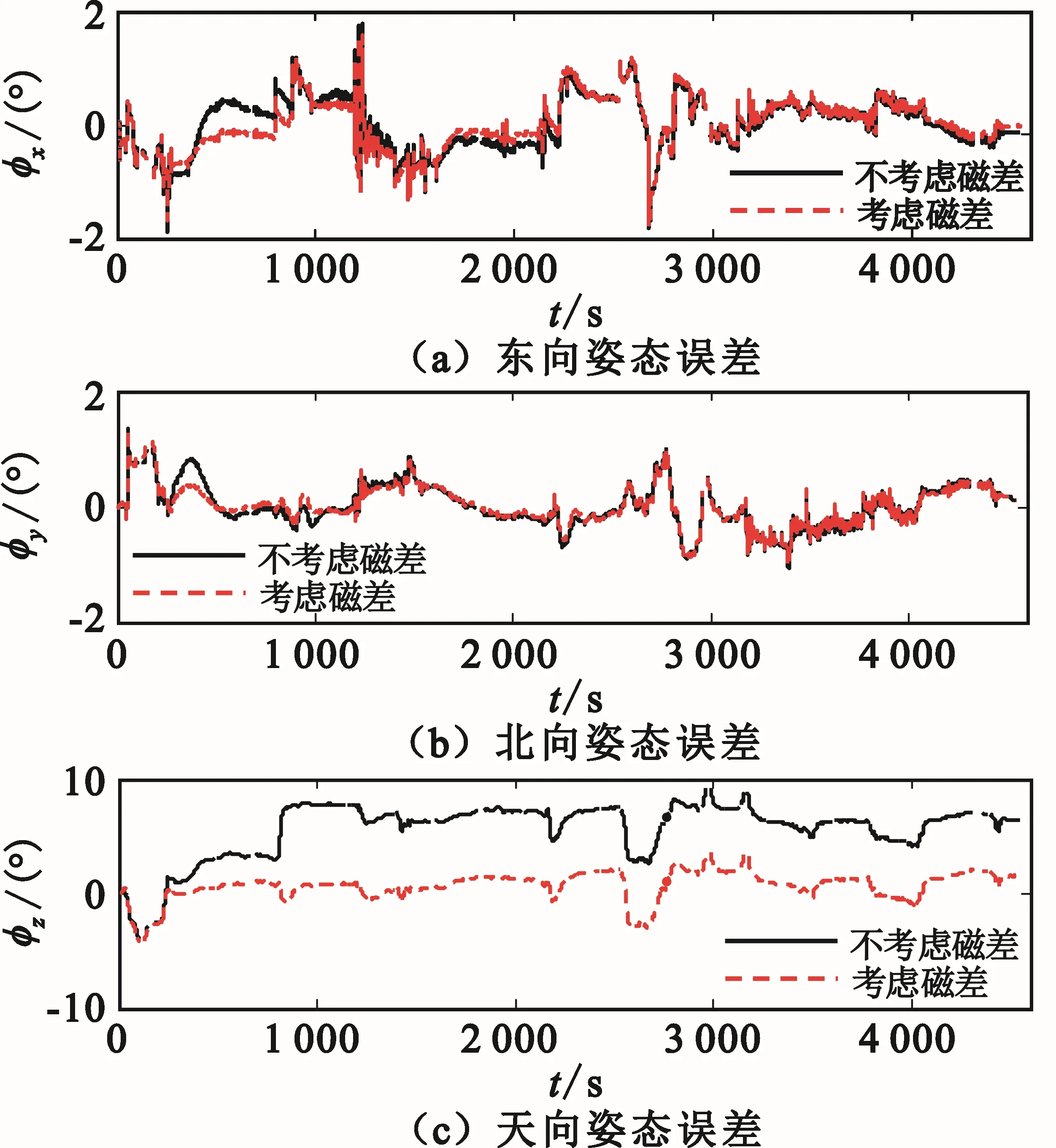
图6 两种测试条件下的姿态误差曲线
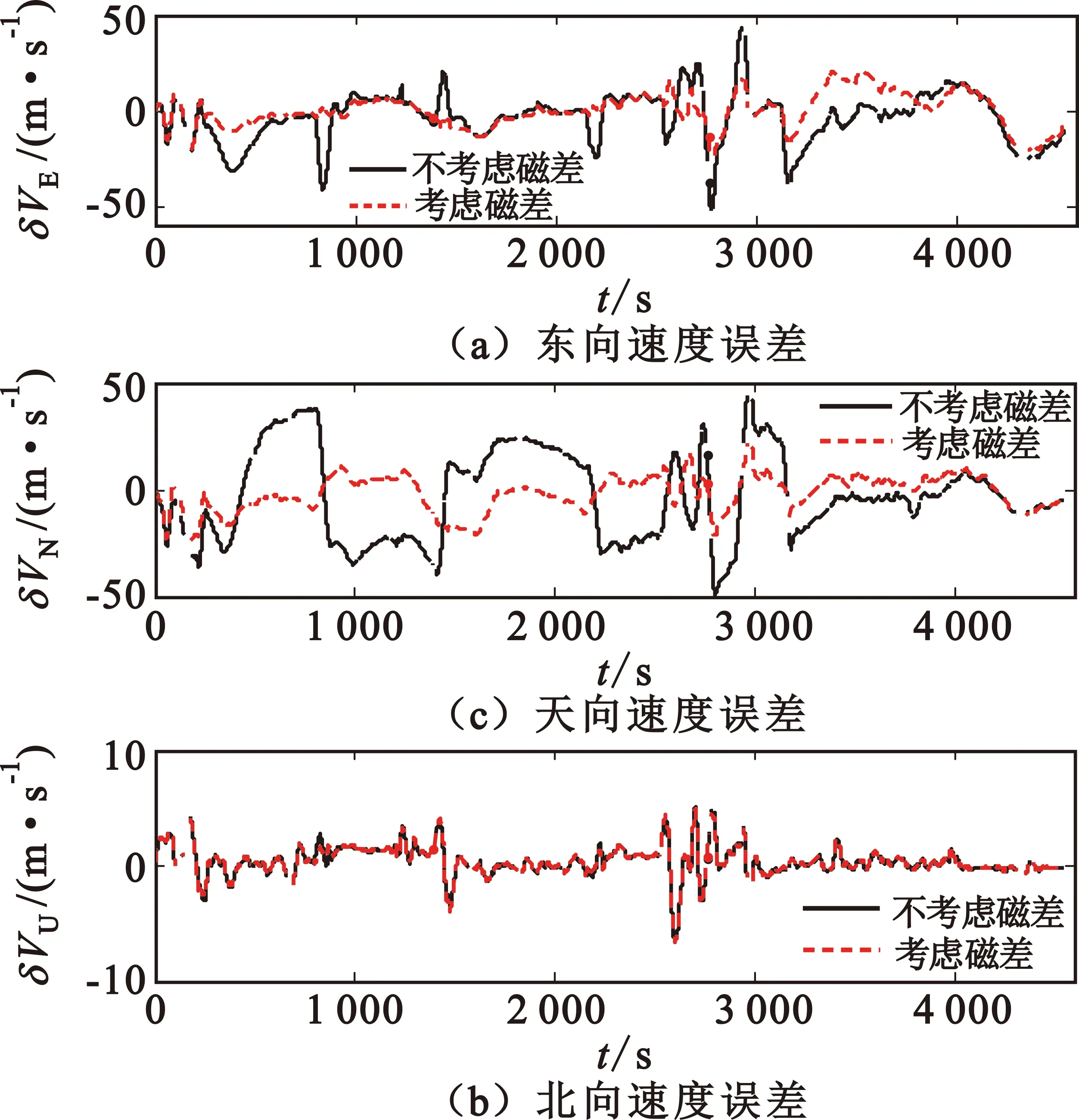
图7 两种测试条件下的速度误差曲线
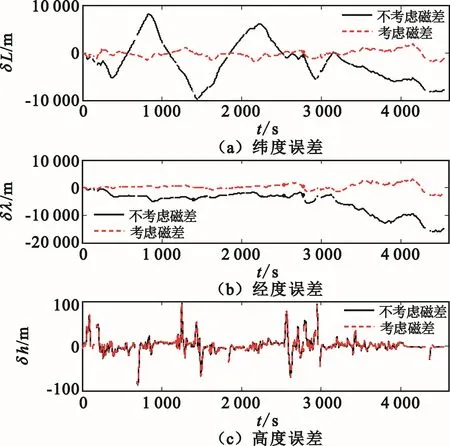
图8 两种测试条件下的位置误差曲线
两种测试方案下导航参数误差的均方根值如表1所示。

表1 两种测试方案下导航参数误差的均方根值
如图5所示,本文所设计的组合导航方案可以较为准确地估计出台站磁差,随估计时间的变长估计精度越高。由图6~8以及表1可知,实际工程应用中,若在组合导航算法的设计中不考虑台站磁差,系统导航精度将受到显著影响。本文在组合导航算法的设计中考虑了台站磁差,相较于不考虑磁差的情况,系统导航精度得到了显著的提升,在方位、水平速度和水平位置的精度提升方面效果更为明显。
在测试中,一个需要值得关注的现象是,随着磁差设置值的增大,磁差估计精度会越来越高。设置磁差理论真值从1~11变化,图9给出了磁差估计精度随磁差设置值变化的曲线,横轴表示磁差理论真值设置值,纵轴表示磁差估计值与理论真值的比值。
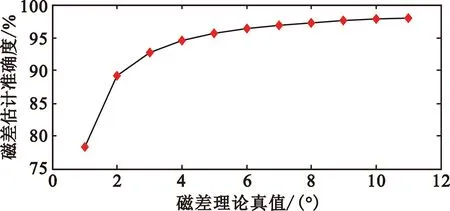
图9 磁差估计精度
综合上述分析,本文所设计的算法可以有效地估计出台站磁差,具备提升组合导航性能的能力。
4.2.2 方位野值对组合导航系统影响测试
本小节测试方位测量野值对组合导航系统的影响,重点测试采用基于M估计的卡尔曼滤波和经典卡尔曼滤波算法时组合导航系统的精度。VOR台站的磁差设置为-5°,两种滤波算法下的组合导航系统的姿态误差、速度误差和位置误差如图10~12所示,两种滤波算法下导航参数误差的均方根值如表2所示。
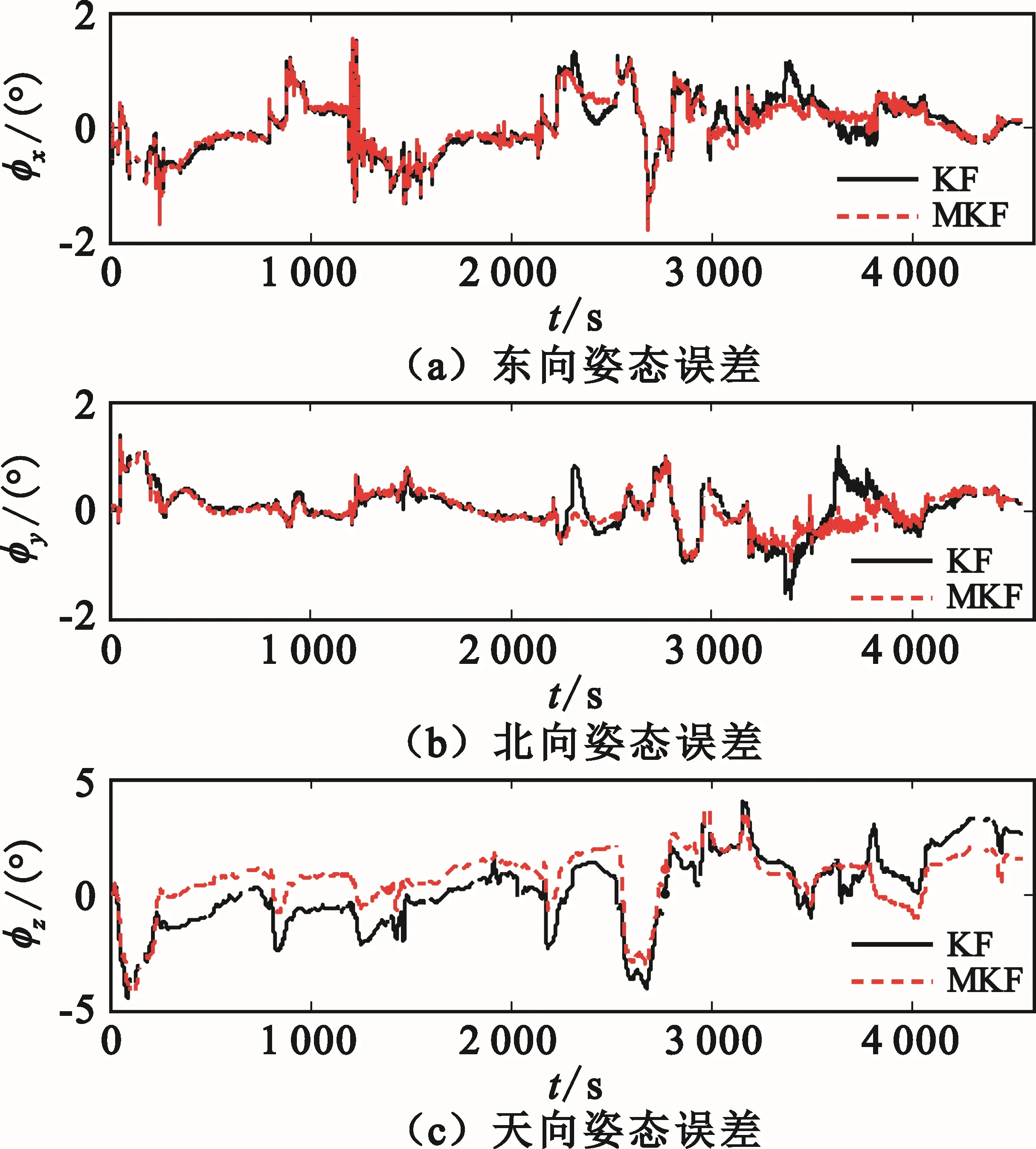
图10 两种滤波算法下的姿态误差曲线
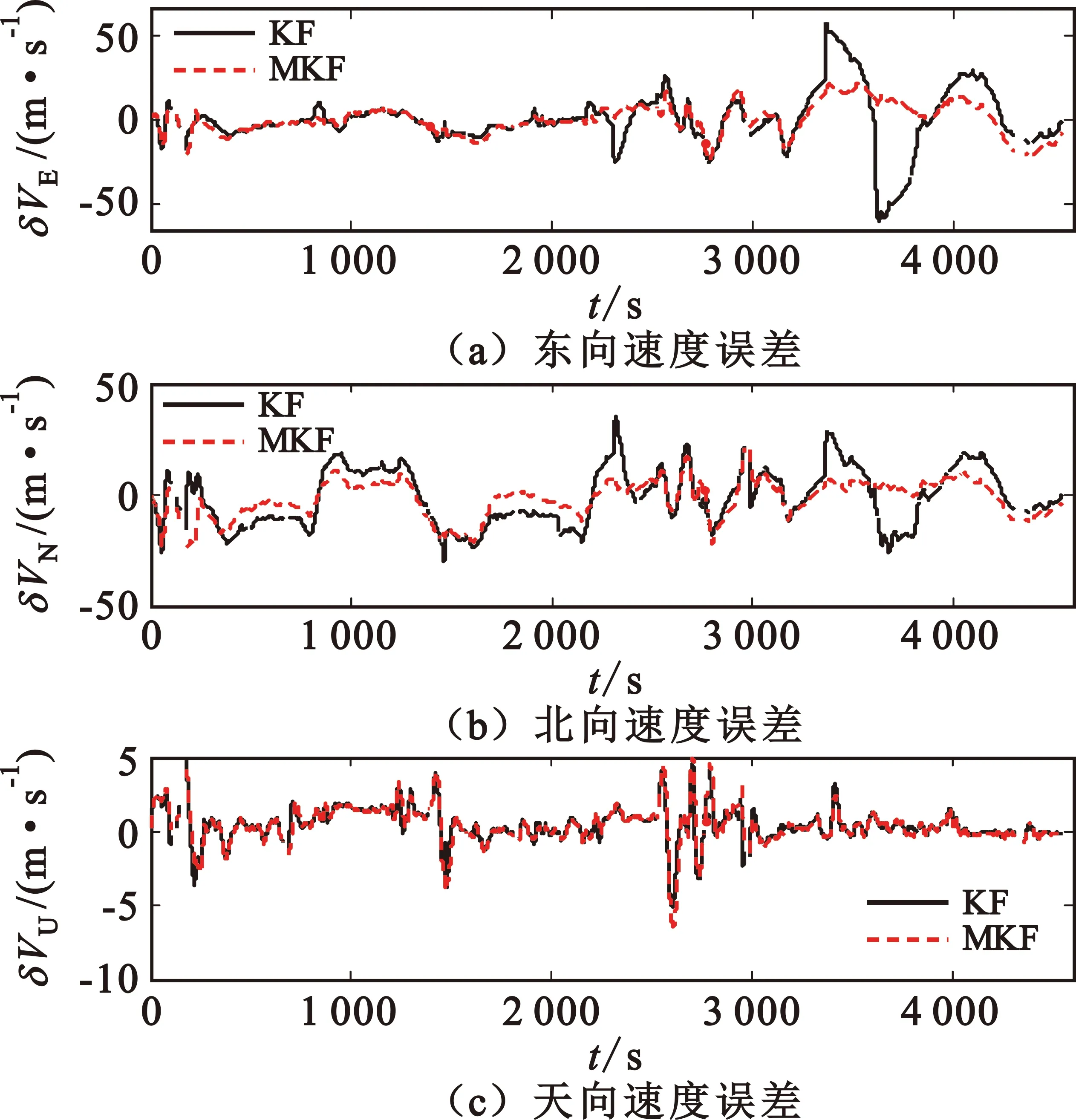
图11 两种滤波算法下的速度误差曲线
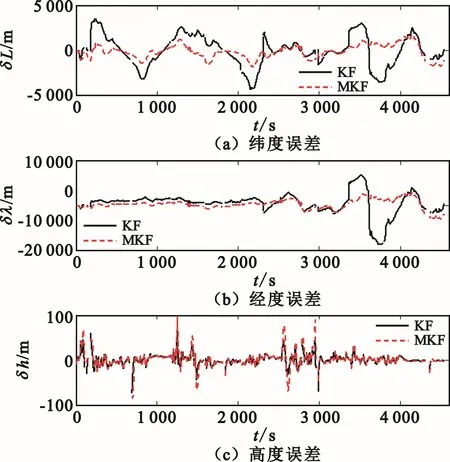
图12 两种滤波算法下的位置误差曲线

表2 两种滤波算法下导航参数误差的均方根值
由图10~12以及表2可知,当VOR输出的方位测量值存在野值时,基于经典的卡尔曼滤波算法实现DEM/VOR/SINS组合导航的导航精度严重恶化,原因在于量测野值的存在破坏了理想的高斯分布框架,导致卡尔曼滤波的状态估计性能严重降低;基于M估计的卡尔曼滤波算法在以上测试条件下表现出良好的鲁棒性,由于该算法是一种组合1范数和2范数的组合估计技术,保证了DME/VOR/SINS组合导航系统在存在野值时仍然具备较好的状态估计性能,相较于前者,基于M估计实现的组合导航系统具有更高的导航精度。需要补充的一点是,VOR输出的方位测量野值通常只在飞机飞行至顶空盲区附近才会出现,当飞机飞行至离台较远的航路阶段,其输出往往较为稳定。当方位测量值不存在野值时,基于M估计的卡尔曼滤波退化为经典的卡尔曼滤波,此时采用两类滤波算法可获得一致的组合导航精度。因此,本文采用基于M估计的卡尔曼滤波实现DEM/VOR/SINS组合导航具备更强的普适性。
5 结 论
本文针对DME/VOR/SINS组合导航系统展开研究,并通过实验验证了所设计的组合导航算法的有效性,主要结论如下:
(1)VOR输出的方位是以台站磁北为参考的,以VOR输出的磁方位作为真方位进行组合导航,由于忽略了台站磁差,组合导航系统的导航精度大幅降低;
(2)飞机飞行至台站顶空盲区附近时VOR输出的方位测量值中包含野值,由于方位测量野值的存在,采用常规的KF实现DME/VOR/SINS组合导航时导航误差急剧增大,导航参数输出不可用;
(3)为减少台站磁差对组合导航算法的影响,本文所设计的组合导航算法将台站磁差纳入参数估计的范畴,在信息融合处理中为应对方位测量野值对导航精度的影响,采用了基于M估计的卡尔曼滤波算法实现了组合导航。上述两方面的改进工作提高了组合导航算法的适用性和鲁棒性,具备较高的工程应用价值。

