基于瞬时相位余弦的探地雷达多层路面自动检测
周东, 刘毛毛, 刘宗辉, 刘保东
(1.广西大学 土木建筑工程学院,广西 南宁 530004; 2.广西大学 广西防灾减灾与工程安全重点实验室,广西 南宁 530004; 3.南宁城建管廊建设投资有限公司,广西 南宁 530219)
0 引言
探地雷达作为一种快速无损的地下目标检测技术,近年来已经在路面病害定位和层厚检测中得到广泛应用[1-4]。然而,目前探地雷达路面层位提取主要依靠解释人员的经验或相关算法,人工或半自动拾取雷达剖面中强振幅同相轴连续的层位信息,存在主观性强、解释周期长、工作量大和每次仅能追踪一个层位等缺点。因此,有必要研究一种路面多层位自动追踪方法。
目前探地雷达层位识别和标定主要是借鉴发展较为成熟的地震层位追踪方法,基于波形相似特征[5]、人工神经网络[6]或图像特征[7-8]自动拾取层位信息。由于地震波与电磁波在理论和数据处理中存在诸多相似性,已有许多学者将地震层位追踪方法引入至探地雷达领域[9-12]。在路面检测方面,Lahouar等[13]基于振幅阈值来检测探地雷达强反射信号,并使用合成的子波信号与反射信号进行相似计算来识别层反射数据。Loizos等[14]采用不同的介电常数估算方法对比分析了路面沥青层厚度估算的准确性。周辉林等[15]通过层界面检测和模式识别等技术提取了探地雷达路基层厚特征,并在此基础上研究了基于SVM的路基病害自动检测算法。Le等[16]同样基于SVM研究了探地雷达道路基层厚度的估计方法。Zhao等[17]研究了基于正则化反褶积技术的探地雷达沥青层厚度预测算法。虽然已有许多学者采用不同方法对路面厚度和病害检测展开了研究,并取得了一定进展,但目前方法主要集中在单个层反射界面识别,且大多未考虑地下层界面同相轴反射的极性信息。
基于此,本文提出了一种快速、准确的公路路面探地雷达多层位自动检测方法。首先利用复信号分析获取了探地雷达数据的瞬时相位余弦,并将其与合成的子波余弦矩阵数据进行相似度分析后再计算瞬时相位余弦,提高相位同相轴的横向连续性。根据深度方向相邻层位线的振幅均方根平方值来确定层位数据,并通过设置层位线阈值和幅值阈值来过滤无关或不重要的层位数据。最后通过室内数值模拟和现场探地雷达数据对本文方法的有效性和适应性进行了验证。
1 方法理论
1.1 瞬时相位余弦
探地雷达采集得到的实信号可以表示如下:
y(t)=A(t)cos[ω0t+φ(t)] ,
(1)
式中:A(t)是关于时间t的函数,为瞬时振幅,主要与地下介质电磁衰减特征和增益方法等有关;cos[ω0t+φ(t)]为瞬时相位余弦;[ω0t+φ(t)]为瞬时相位;ω0为中心频率;φ(t)为关于时间t的相位函数。
为获取探地雷达数据的瞬时相位余弦信息,需要将探地雷达数据进行Hilbert变换后构造复信号,在复信号分析中利用瞬时振幅和实信号来获取瞬时相位余弦。实信号经Hilbert变换后可表示为
(2)
由式(1)、(2)可以得到瞬时振幅:
(3)
瞬时相位余弦:
(4)
式中,实信号瞬时振幅不能为0,虽然在实际信号分析中这种情况很少,但若存在这种情况时瞬时相位余弦值应置为0。
图1显示了一个归一化的雷达子波波形及其瞬时相位余弦波形。图中可以看出瞬时相位余弦波形的波峰、波谷和零值点位置与子波具有较好的对应关系。由于该子波最大振幅绝对值在波峰处,因此在本文中认为该子波的相位极性为正相位。

图1 雷达子波及其瞬时相位余弦
1.2 瞬时相位余弦横向增强处理方法
探地雷达在实际工程应用中,受现场探测环境和天线自身耦合干扰,采集得到的数据中往往会包含有衍射干扰。衍射干扰会使得同相轴局部不连续,给基于相位特征的层位自动追踪造成困难。由于公路路面的探地雷达数据主要是横向层分布,因此在进行层位识别前,增强相位横向连续性是有必要的。
地下层分布介质的雷达反射波形在测线方向上具有连续性、渐变性和相似性等特点,而且反射波波形会保持对称的Ricker子波[13]。由于瞬时相位余弦相当于将雷达信号在波峰和波谷处进行归一化,降低了层反射数据的波形偏差,使得层反射数据与Ricker子波的瞬时相位余弦具有较高的相似度。若将子波瞬时相位余弦数据在测线方向上进行拓展,并将其与雷达反射数据进行相关性分析,则横向层分布的反射数据会具有较高的相似性。若在此基础上重新计算相关分析后的瞬时相位余弦,则能够进一步降低测线方向上的波形偏差,增强横向同相轴的连续性。两个相同大小数据的相关系数可通过
(5)
为增强余弦剖面同相轴的横向连续性,本文提出了一种瞬时相位余弦横向增强处理方法。该方法在获取探地雷达数据的瞬时相位余弦后,主要处理步骤如下:
1)构建标准核矩阵。设置一个大小为m×n的标准子波瞬时相位余弦矩阵作为标准核矩阵,其中m为波长大小;n为测线方向上拓展的道数,值越大,横向增强能力越强,但垂直分辨率越低。
2)计算相关系数矩阵。对于瞬时相位余弦数据中某样点,选取以该样点为中心、大小为m×n的窗口数据,计算该窗口数据与标准核矩阵的相关系数值并代替该样点。
3)再次计算瞬时相位余弦。计算相关系数矩阵数据的瞬时相位余弦,即可得到横向增强处理后的结果。
1.3 层位自动识别方法
为减少解释人员主观判断的影响,提高公路路面探地雷达层位识别精度,文中提出了一种基于瞬时相位余弦的探地雷达层位自动识别方法。对于一个大小为M×N的雷达数据,首先计算其瞬时相位余弦,获取各道瞬时相位余弦的极值点及空间位置信息。将获取的相位极值点采用二值化的方法保存在矩阵C中(大小为M×N),0表示该点瞬时相位余弦为非极值点,1表示极值点(波峰或波谷)。
为方便后续层位追踪和极性识别,在相位极值数据中将具有相同极性的点进行连线。具体方法是:以相位极值点为中心,设置深度方向搜索窗口大小,追踪测线方向相邻道具有相同极性的层位极值点,并将追踪得到的相位极值点连接为层位线。为防止层位线追踪出现串层和偏离,仅追踪搜索窗口内只有单个极值点时的数据。根据层反射单个波长内相邻相位极值点距离约为1/4波长的特点,搜索窗口大小一般设置为1/8~1/4波长。
在本文中,基于反射波的波形特点,认为层位点在反射波的绝对振幅最大值处,并且该层位点的极性取决于绝对振幅最大值处的瞬时相位余弦值。实际层位线提取需要设置一个大小为1~1.5倍波长的深度搜索窗口,若某一层位线在深度搜索窗口内存在上一条和下一条层位线,并且该层位线上的振幅均方根平方值大于另外两条层位线上的振幅均方根平方值,则保留该层位线数据。深度搜索窗口设置为1~1.5倍波长主要是为了防止出现层位追踪串层,并且尽量包含完整的子波反射特征。
为减少一些无关(不重要)的同相轴反射数据,可以通过设置层位线阈值Lmin过滤一些长度较短的层位线数据。对于层分布较广或密集采样的雷达数据,层位线阈值应适当增大。此外,在实际工程应用中,由于层反射分界面两侧存在介电差异,层反射信号幅值相对较大,而背景或噪声数据的信号幅值相对较小。因此,可以通过设置振幅阈值Amin来进一步去除幅值较小的层位线。经过上述步骤,能够追踪得到强反射区域层位线数据及其极性。
对于输入的探地雷达数据,本文层位自动追踪方法主要步骤如下:
1)获取瞬时相位余弦信息。计算雷达数据的瞬时相位余弦,并进行横向增强处理,记录瞬时相位余弦极值点对应的空间位置、振幅和极性信息。
2)层位追踪。设置搜索窗口大小,追踪测线方向上相邻道相同极性的数据,并连接为层位线。
3)层位识别。设置深度搜索窗口大小,若某层位线在深度窗口内存在上一条和下一条层位线,并且该层位线上的振幅均方根平方值大于相邻的另外两条层位线,则认为该层位线为有效层位线,保留该层位线。
4)层位线过滤。根据设置的层位线阈值和振幅阈值去除较短和幅值较弱的层位线。
5)极性识别。层位线对应的瞬时相位余弦值大于0为正相位,反之为负相位。
2 数值模拟
为验证本文方法的可靠性,利用GPRMAX 3.0[18]软件模拟了一个地下多界面反射数据,几何模型如图2所示。模型大小为13.0 m×5.0 m,网格为0.005 m×0.005 m。几何模型中主要包括3层反射介质,在第二层中包含了2个具有相同层厚的倾斜介质,各层介质均为各向同性、不导电、非磁性的材料,从上到下各层介质的介电常数分别为6、4、8、6。雷达天线从模型上方0.5 m的空气层底部由左至右水平移动,发射和接收天线间隔0.4 m,激励源为 200 MHz 的Ricker子波。采样时窗为100 ns,每隔 0.1 m采集一道数据,共采集了130道数据。此外,为避免边界效应,实际模型区域在各边界处向外延伸了2 m。

图2 数值模拟几何模型
图3a为纯净数值模拟雷达剖面,可以看出图中除了由反射面产生的同相轴反射外,还存在一些幅值较弱的伪影反射。为使模拟结果更接近实际情况,在数值模拟结果中添加了信噪比为15 dB的高斯白噪声。在添加高斯噪声后,伪影反射基本被遮蔽,但大致能看出几何模型的边界分布范围(图3b)。由于第二层右侧介质的介电常数高于模型其他介质,电磁波在该介质中传播时速度较慢,因此在雷达剖面中该区域上下反射界面更远。

a—纯净无噪声数据;b—添加高斯噪声
图4为图3b含噪数据的瞬时相位余弦及其横向增强处理后的结果。由图可见,噪声的存在同样使得瞬时相位余弦剖面中的同相轴反射大量被遮蔽,不利于基于同相轴的层位追踪(图4a)。而横向增强处理后,瞬时相位余弦剖面中同相轴的连续性得到提高,同相轴反射特征得到显著增强,有利于进一步的层位追踪(图4b)。
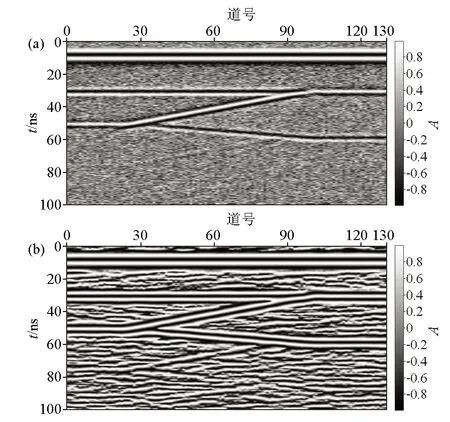
a—横向增强处理前;b—横向增强处理后
利用本文方法追踪了图3b含噪数据的层位,结果如图5所示。层位追踪结果与模型分界面反射基本一致,其中黄、红两种颜色分别表示该层位为正、负相位极性。各界面处反射波的相位极性取决于分界面的反射系数,如第一个分界面ε1>ε2,此时反射系数为正,相位极性与入射波一致。而第二个分界面ε1<ε2,反射系数为负,相位极性与入射波相反。数值模拟试验表明本文层位追踪方法不仅能够准确自动识别出多个层位数据,还可以识别出层位的极性。

图5 层位追踪结果
3 现场案例
选取广西北海市城市公路路面探地雷达数据进行测试,该公路结构包括沥青面层、混凝土基层和水泥稳定碎石层。探地雷达采集仪器选用意大利IDS公司生产的K2型探地雷达,天线中心频率为900 MHz。现场采集设置的时窗为60 ns,每道采集512个样点,每米采集20道。为更好显示路基探地雷达特征,本文后续仅展示前256个样点(30 ns)数据。
图6为原始探地雷达剖面及其测线第15 m处的单道波形。从图中可以看出该区域主要存在2个相对平行的层反射,第一层和第二层反射波形状均与Ricker子波类似,其中第一层反射在10~30样点之间,第二层反射在60~80样点之间。此外,单道波形图中还可以看出上下两层反射信号的最大绝对振幅分别在波谷和波峰处,可知上下两层反射信号的极性相反。这是因为当电磁波从沥青面层(相对介电常数为3~5)传播至混凝土基层(相对介电常数为6~9)时,反射系数为负,反射波的相位与入射波相反。而电磁波由混凝土基层传播至水泥稳定碎石层(相对介电常数为4~6)时,反射系数为正,此时反射波的相位与入射波相同,因此第一层与第二层的同相轴反射相位极性出现反转。

图6 原始雷达剖面和测线第15 m处单道波形
为验证本文瞬时相位余弦横向增强处理方法的有效性,分别追踪了原始雷达数据瞬时相位余弦横向增强处理前、后的层位,结果如图7所示。图中可看出未经横向增强处理的层位追踪结果存在局部不连续现象,而经横向增强处理后第一层和第二层的层位线更加连续、完整,表明瞬时相位余弦横向增强处理有助于提高层位线追踪的连续性。此外,从图中还可以看出第二层层位线起伏较大,在其下方还存在一条较短的正相位层位线。表明该区域混凝土基层存在局部沉降现象,根据相位极性可知下方较短的层反射界面下方介质的介电常数小于水泥稳定碎石层,并且该异常体反射信号幅值较强,因此推断该异常反射体可能为局部脱空。经室内测试,本文方法层位点拾取窗口大小设置为5,层位线长度阈值为150,幅值阈值为原始雷达数据的绝对平均幅值。

图7 横向增强处理前(a)后(b)层位追踪结果对比
为进一步检验本文层位追踪方法的有效性,将其与目前常用的基于波形相似特征的层位自动追踪方法进行对比,结果如图8所示。图中青色星号为传统基于波形相似方法层位追踪的种子点,第一层和第二层种子点分别为(22,800)、(68,800)。从图中可以看出传统方法追踪第一层层位时,在剖面左侧和右侧均出现了层位追踪偏离现象,而在追踪第二层层位时存在层位追踪串层现象。而本文方法不需要设置种子点,降低了人为干预成本,还能够自动提取异常体强振幅同相轴反射的层位数据。现场案例分析结果验证了本文方法的有效性和适应性。

图8 两种方法层位追踪结果对比
4 结论
针对传统层位追踪方法普遍存在主观性强、耗时耗力和每次仅能追踪1个层位等问题。本文提出了一种探地雷达公路路面多层位自动追踪方法。通过复信号分析获取了雷达数据的瞬时相位余弦,并通过构建子波余弦矩阵对瞬时相位余弦进行横向增强处理,提高了相位数据同相轴反射的横向连续性;基于反射信号波形类似Ricker子波的特点,利用雷达数据的波峰、波谷、幅值和极性等信息来确定层位数据;最后根据层位线阈值、振幅阈值过滤一些无关或不重要的层位线,实现有效强反射同相轴层位自动追踪。数值模拟和现场案例分析结果验证了本文方法的有效性和适应性。本文方法不仅可以自动追踪多个层位数据,还可以估计出层位的极性,研究成果可为探地雷达地层分析、层反射介质反演、沉积体系域解释提供技术支持。

