Mathematica在材料力学弯曲问题中的应用

曹建华,郭东旭

（黄山学院，安徽 黄山 245041）

0 引 言

对于机械类、材料类等专业，材料力学是一门必修的专业基础课，而弯曲变形在材料力学中所占篇幅非常大，其所研究的问题是学生学习的难点。弯曲变形所研究的问题包括剪力，弯矩、转角′（）和挠度（）的求解，一般采用截面法或积分法方法。积分法是利用剪力、弯矩、转角′（）和挠度（）与分布载荷（）的积分关系，在作用载荷连续的一段梁内会产生4个常数，当梁上出现不连续载荷时，如梁上作用着多个集中外力、多个集中外力偶，或者作用在多个不连续局部的分布载荷，需要分段写出剪力，弯矩、转角′（）和挠度（）等方程。假设载荷不连续的梁分成段求解，需要4个常数需要确定，是一个繁重的任务，且容易出错。文献[1]应用奇异函数法求解了一根直梁，也没有相应的程序代码。本文在详述奇异函数性质的基础上，应用奇异函数法求解了一根或多根杆件组成的直梁弯曲变形问题，与文献对比进行验证，最后应用Mathematica数学软件实现奇异函数法求解弯曲变形问题的过程。

1 奇异函数性质

1.1 δ函数、单位阶跃函数和单位斜坡函数

(1)狄拉克函数(Dirac Delta function)，具有如下性质：

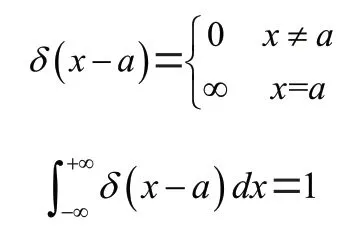
(2)单位阶跃函数（unit step function）（-）为：

(3)单位斜坡函数（unit ramp function）（-a）为：

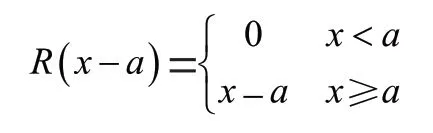
狄拉克函数（-）与单位阶跃函数（-）的关系为：

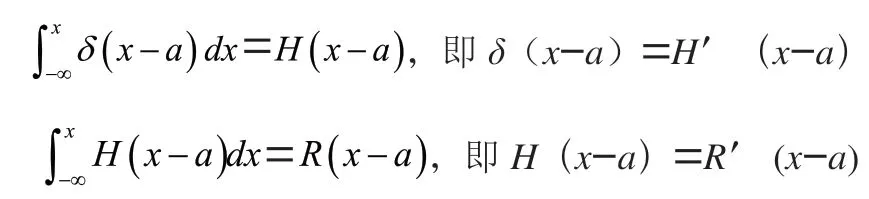
1.2 奇异函数的定义

奇异函数定义如下：

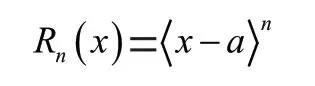
其中，为整数，且当≥0时

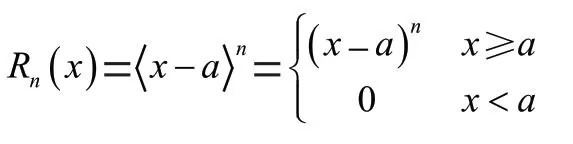
当＜0时

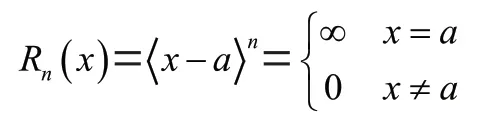
由以上定义可知如下关系：

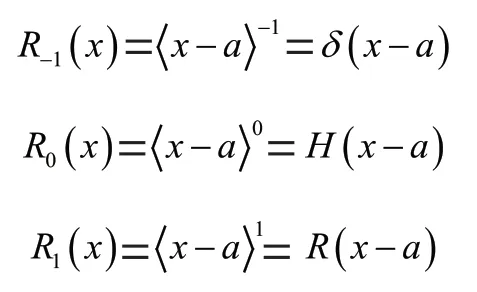
由定义可知，奇异函数有如下性质：

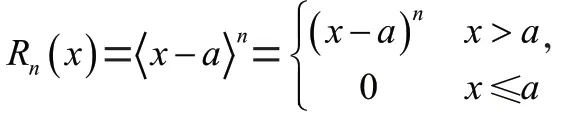
（2）当≥0时，由（1）（2）性质积分可得性质(3)。

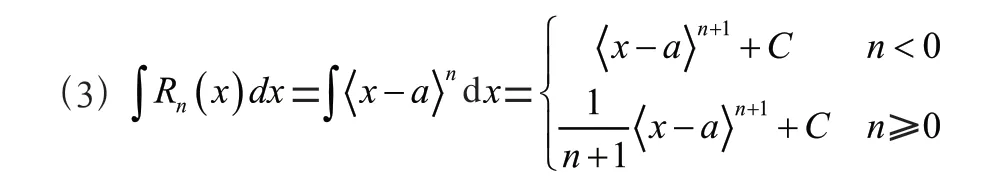
式中，为积分常数。当＜0时，R（0）是没有意义的，不参与计算。

2 应用奇异函数求解梁弯曲变形问题

2.1 梁问题的统一表达式

如图所示，结构由两根梁件通过9 m处的铰链链接在一起，承受有均匀分布载荷，集中外力，集中外力偶、线性变化的分布载荷以及支座反力、固定端约束力。在众多教材中，梁弯曲问题的求解一般步骤如下：

(1)以梁的轴左端为原点，表示沿轴线的横坐标。

(2)按约束（支座和固定端）性质，画出约束反力，并通过平衡方程求解约束反力。

(3)对不连续载荷进行分析，计算载荷不连续处总数，则需要分-1段。如图1所示，载荷不连续处包括分布载荷的起始终止处、集中外力处、集中力偶处、铰链连接处和支座反力、固定端处，如果不连续处重叠（如3 m处支座反力和分布载荷终止处重合），算作1处不连续处，总共有7段不连续处，需要分6段。

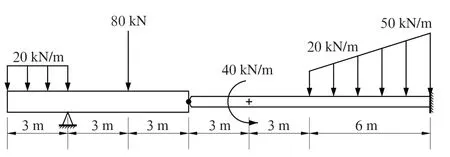
图1 受多个载荷的梁

(4)分段进行求解出剪力，弯矩、转角′（）和挠度（），通过边界条件求出积分数。

梁和梁的坐标系如图1所示。以梁的轴左端为原点，表示沿轴线的横坐标，表示梁的轴线挠度，向下为负。图2显示弯矩和剪力的符号规定。本文中，规定作用在梁上的集中外力和分布外力向下为正，逆时针方向的力偶为正。

图2 梁的内力正方向

设（）代表梁上某一连续段（，）的载荷集度，符号规定如下：向上的载荷为正，顺时针的力偶为正，反之为负。

在＜＜梁内，剪力和分布载荷函数的积分关系表示如下：

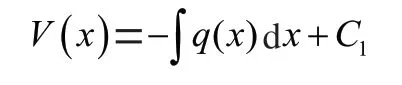
其中为常数。对上式再次积分，可得弯矩表达式为：

由 = 可知，通过积分可得转角′（）和挠度（）表达式：

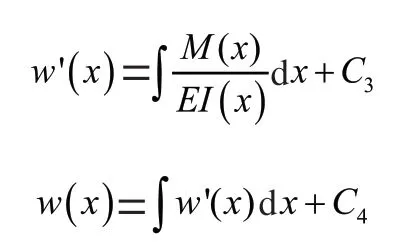
其中，、、、为积分常数，（）是梁的抗弯刚度。

由以上可知，如果将梁上的所有不连续载荷都能包含在载荷函数（）表达式中，就能够无需分段，并求出剪力，弯矩、转角′（）和挠度（）。奇异函数具有将不连续载荷包含在一个表达式并进行计算的能力，将不连续的问题变成了连续问题处理，简化了很多计算。下面叙述采用奇异函数法来表示（）。

(1)作用于=处的集中外力，其载荷函数）表达式为：

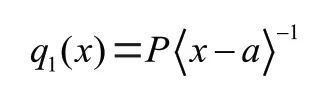
(2)对于在区间[，]内线性变化的分布载荷：

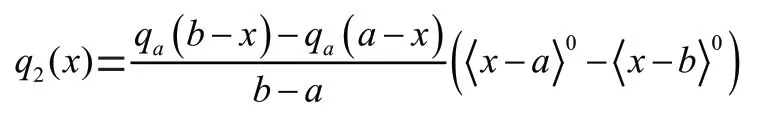
(3)若是在区间[，]的分布载荷函数F（），载荷函数（）表达式为：

(4)作用于=处的集中外力偶，其载荷函数（）表达式为：

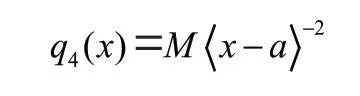
(5)=（0＜＜）处铰链连接处或剪力连接，在此处截面转角发生突变，其载荷函数（）表达式为：

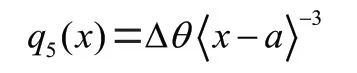
(6)=（0＜＜）处弯矩连接，在此处截面处位移发生突变，其载荷函数（）表达式为：

2.2 梁的边界条件

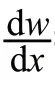
(2)刚性支撑：=0，如图1中3 m处的支撑。

(3)左端简支边界：=0，+M=0（M为作用于左端的集中外力偶），如图3中左端边界。

图3 弯矩连接的梁

(4)右端简支边界：=0，-M=0（M为作用于右端的集中外力偶）。

(5)左端自由边界：+V=0，+M=0（M、V为作用于左端的集中外力偶和集中外力），如图1中左端边界。

(6)右端自由边界：-V=0，-M=0（M、V为作用于右端的集中外力偶和集中外力）。

(7)左端引导边界：+V=0，=0（M、V为作用于左端的集中外力偶和集中外力）。

(8)右端引导边界：-V=0，=0（M、V为作用于右端的集中外力偶和集中外力），如图4所示。

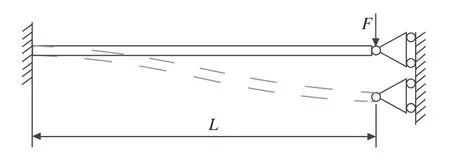
图4 右端是引导边界的直梁

(9)铰链连接（a hinge or moment release）：=0，如图1中9 m处连接，只能传递剪力，不能传递弯矩。

(10)弯矩连接（shear release）：=0，如图3所示，只能传递弯矩，不能传递剪力。

2.3 梁问题的求解步骤

用奇异函数法求解剪力，弯矩、转角′（）和挠度（），步骤如下：

(1)建立坐标系，默认以左端点为原点，平行于轴线为轴。

(2)奇异函数写出沿梁长度的载荷集度（）。

(3)代入边界条件，求出常 数、、、以及Δ、Δ。

(4)作出剪力，弯矩、转角′（）和挠度（）图形。

3 求解实例及Mathematica求解

3.1 求解实例的演算过程

如图5所示，承受两根杆件组成的直梁，通过铰链连接，承受2个集中外力。本实例来自刘鸿文《材料力学.I》6版中习题4.6(b)。

图5 梁的几何和受力

解：第一步：写出梁的载荷函数：

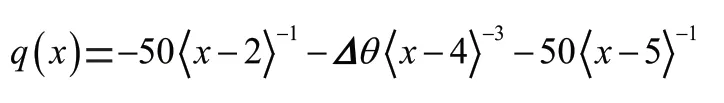
第二步：根据载荷函数，通过积分写出剪力，弯矩、转角′（）和挠度（）的方程分别为：

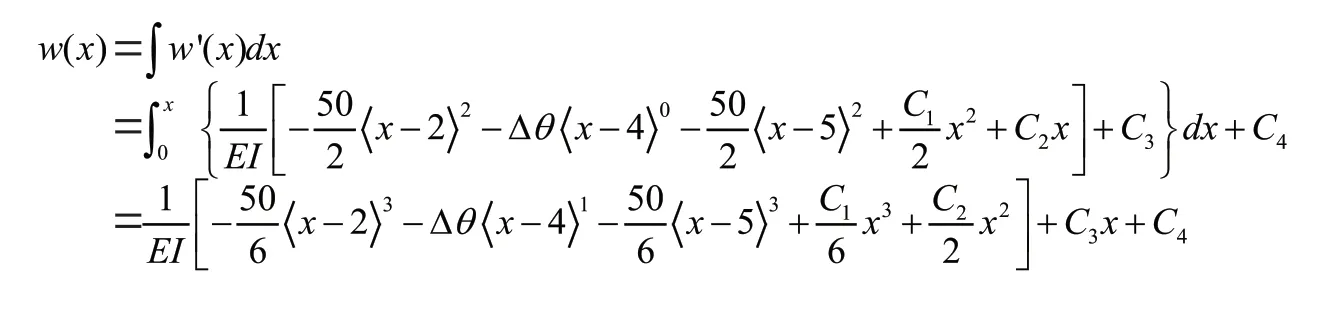
第三步：写出边界条件，并代入第二步中相应的四个方程中，求出积分常数。本题是两端简支梁，其边界条件为：

x=0，U=0，S=0

x=6，U=0，M=0

x=4，M=0

代入第二步中相应的方程，可得：

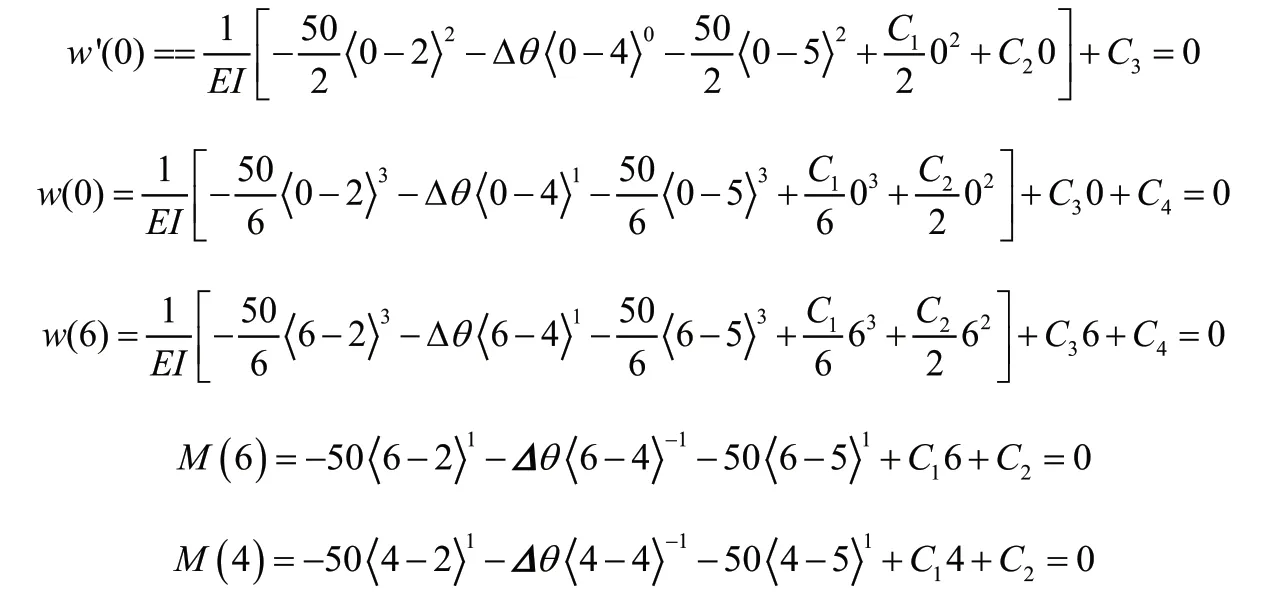
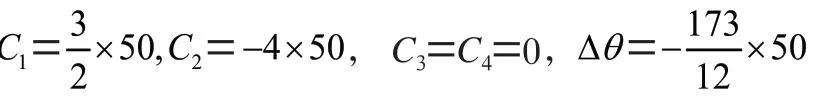
第四步：将第三步所求出的常数代入第二步的方程中，可得弯曲问题的方程，同上，略去不表。

3.2 Mathematica实现奇异函数法

Mathematica具有强大的数值和符号计算能力、强大的图形功能等，深受广大从事科研和工程人员的欢迎。Mathematica有内置函数DiracDelta实现δ函数，HeavisideTheta函数实现单位阶跃函数。当n＜-1时，R（x-a）可以用DiracDelta导数表示，非常方便。下面是基于Mathematica软件实现的奇异函数法程序代码，只需要根据具体问题，修改粗体部分数据，即可用于求解任意直梁弯曲问题。代码内容如下：

Clear[“Global`*”]

SetDirectory[]

(*集中外力对应的载荷函数q(x) *)

Fc[{P_, a_}][x_] := -P DiracDelta[-a + x];

(*分布载荷对应的载荷函数q(x) *)

Fdist[{p_, a_, q_, b_}][x_] := -((b p - a q - p x + q x)(HeavisideTheta[-a + x] - HeavisideTheta[-b + x]))/(-a + b);

(*集中外力偶对应的载荷函数q(x) *)

Cp[{M_, a_}][x_] := -M DiracDelta’[x - a];

(*铰链连接对应的载荷函数q(x) *)

Sc[{dtheta_, a_}][x_] := -dthetaDiracDelta’’[x - a];

(*弯矩连接对应的载荷函数q(x) *)

Mc[{dw_, a_}][x_] := -dwDiracDelta’’’[x - a];

(*梁的边界条件和参数输入 *)

bnd={“Fixed”,”Pinned”};(*边界条件设置*)

Le=6; (*梁的总长*)

EI=1; (*梁的抗弯刚度，为了方便设为1*)

PointLoad={50,2,50,5};(*集中外力设置*)

LineLoad ={};(*分布载荷设置*)

PointCouple= {} ; (*集中外力偶设置*)

InSpan ={};(*刚性支撑设置*)

ShearConnection ={4};(*铰链连接设置*)

MomentConnection = {};(*弯矩连接设置*)

(*生成由载荷函数各项组成的链表*)

px = Join[

Map[ Fc[#1][x] &, DeleteCases[Join[Partition[PointLoad,2],InSpan], {_, 0 | 0.0} | {_, Le}] ],

Flatten[Map[ Fdist[#1][x] &, Partition[LineLoad, 4] ]] /.HeavisideTheta[x - Le] :> 0,

Map[ Sc[#1][x] &, ShearConnection ],

Map[ Mc[#1][x] &, MomentConnection ],

Map[ Cp[#1][x] &, DeleteCases[ Partition[PointCouple, 2],{_, 0 | 0.0} | {_, Le} ]]

];

(*通过积分求解剪力表达式*)

V=Append[Integrate[px, x], c1];

(*通过积分求解弯矩表达式*)

M = Append[Integrate[V, x], c2];

(*通过积分求解转角表达式*)

S = Append[Simplify[ (Integrate[ Flatten[Map[Times[1/EI, #1]&, M]], x ] /. urule[x, Le]) /. HeavisideTheta[x +a_] ->HeavisideTheta[x + a/Le] ] /. HeavisideTheta[x + a_]->HeavisideTheta[x + a *Le], c3];

(*通过积分求解挠度表达式*)

U = Append[Integrate[S, x], c4];

(*取出左端边界上的集中外力和力偶*)

nhL = {Cases[Partition[PointLoad, 2], {_, 0 | 0.0}],Cases[Partition[PointCouple, 2], {_, 0 | 0.0}]} /.{{{P_, _}} :> P,{} :> 0};

(*根据左端边界条件，将x=0代入到所对的条件中，若边界条件中有弯矩和剪力，将左端的集中外力和力偶加进去*)

bndL = Switch[ First[bnd], “Fixed”, {U, S}, “Pinned”,{U, Append[M, Last[nhL]]},

“Free”, {Append[M, Last[nhL]], Append[V,First[nhL]]}, “Guided”, {S, Append[V, First[nhL]]}] /. x -> 0;

(*取出右端边界上的集中外力和力偶*)

nhR = {Cases[Partition[PointLoad, 2], {_, Le}],Cases[Partition[PointCouple, 2], {_, Le}]} /.{{{P_, _}} :> P, {}:> 0};

(*根据右端边界条件，将x=Le代入到所对的条件中，若右端边界条件中有弯矩和剪力，将右端的集中外力和力偶加进去*)

bndR = Switch[ Last[bnd], “Fixed”, {U, S}, “Pinned”,{U, Append[M, -Last[nhR]]},

“Free”, {Append[M, -Last[nhR]], Append[V,-First[nhR]]}, “Guided”, {S, Append[V, -First[nhR]]}] /. x ->Le;

(*将中间刚性支撑，铰链连接，弯矩连接的条件，与边界条件合在一个链表中*)

intList = Join[bndR, bndL, evalIntCon[x, U, InSpan],evalIntCon[x, M, ShearConnection], evalIntCon[x, V,MomentConnection]];

(*将左端边界条件的链表中各项加在一起，并等于0，对右端边界条件，中间刚性支撑，铰链连接，弯矩连接的条件进行同样操作*)

eqns = Thread[ Apply[Plus, intList, 1] == 0 ] /. urule[x, Le] /.{DiracDelta->0};

(*求解上述命令得出的方程*)

soln = Flatten[ Solve[eqns, Join[ {c1, c2, c3, c4}, First /@Join[InSpan, ShearConnection, MomentConnection]]] ];

(*将求解结果代回到V, M, S, U的表达式中*)

res = Apply[Plus, {V, M, S, U} /. {DiracDelta->0} /. soln /.urule[x, Le], 1];

(*绘制剪力图*)

Plot[res[[1]] /. {HeavisideTheta ->UnitStep}, {x, 0,Le},

PlotPoints -> 1500, Frame -> True,

FrameLabel -> {x, “Shear Force”}, LabelStyle -> {12,Bold},

FrameStyle ->Directive[Black, 14, FontFamily -> “Times New Roman”],

Filling -> Axis]

(*绘制弯矩图*)

Plot[res[[2]] /. {HeavisideTheta ->UnitStep}, {x, 0, Le},

PlotPoints -> 1500, Frame -> True,

FrameLabel -> {x, “Bending Moment”}, LabelStyle -> {12,Bold},

FrameStyle ->Directive[Black, 14, FontFamily -> “Times New Roman”],

Filling -> Axis]

(*程序结束*)

运行程序，可得如图6所示的剪力图和弯矩，与文献[5]对比，结果一致。

图6 剪力图和弯矩图

4 结 论

文中在详述奇异函数法理论的基础上，应用奇异函数法，将受弯梁上不连续的载荷写成统一的载荷函数，并通过多个实例的计算进行验证。奇异函数法演算过程无需求解支座反力，无需受力分析，能够求解各类弯曲问题，便于编制统一的计算程序。采用Mathematica数学软件实现了奇异函数法算法，并绘制了弯曲问题的剪力、弯矩、转角和挠度等图形，统一了解决材料力学中各类问题的计算过程，对教与学都有着一定的参考意义。