地裂缝活动对城市连续梁桥作用的力学分析

常曙光,李文阳,徐 强,2,白超宇,石玉玲

(1.长安大学 地质工程与测绘学院,陕西 西安 710054;2.自然资源部地裂缝与地面沉降野外科学观测研究站,陕西 西安 710054)

0 引言

连续梁桥作为城市交通的枢纽工程,在交通中起到至关重要的作用。地裂缝作为一种典型的地质灾害,对各类建筑物均可能产生不同程度的破坏。在地裂缝发育的城市,桥梁作为重要的交通设施,因其工程线型特点不可避免会受到地裂缝的威胁,因此研究地裂缝活动对认识桥梁的变形破坏规律具有非常重要的现实意义。

当前国内外学者对地裂缝进行了大量研究,但主要集中在地裂缝的发育特征、成因机理,以及地裂缝活动对地下结构的影响等方面[1-5],关于桥梁在地裂缝活动作用下变形破坏机制的研究起步较晚,近年来取得了一定成果。石玉玲等[6]通过大比例尺模型试验研究简支梁桥和固接桥在地裂缝活动时桥面板的变形情况,并对二者进行了对比。高虎艳等[7]通过实例论述了西安地裂缝对城市桥梁的破坏方式和破坏程度,提出了使用桥梁结构应对地裂缝活动的总体防治思路。张新广[8]对西安地铁3号线高架段跨地裂缝进行分析,研究结果表明,当基础产生不均匀沉降时采用简支梁桥和线路调坡方案可降低地裂缝对高架线路的影响。张茵涛等[9]开展1∶20的模型试验,研究了高铁桥梁穿越地裂缝带时地裂缝活动对桥墩应力、轨道变形等的影响。庞旭卿等[10]开展1∶5的桥梁结构跨地裂缝模型试验,分析了地裂缝活动时桥面板及桥墩的应变情况,并对桥梁破坏模式进行了探讨。王利洋[11]通过物理模型试验,对不同地裂缝位错量下高铁桥梁整体变形、混凝土桩应力、箱梁应变等进行研究,并进行了数值模拟计算对比。刘海东等[12]通过FLAC3D建立了高铁桥梁跨越地裂缝的数值模型,分析了箱梁的变形和桩基的受力特征。杨涛[13]对高速铁路简支梁桥跨隐伏地裂缝进行模拟计算,分析了地裂缝活动时的箱梁变形、桩基沉降及其内力变化规律。赵凯[14]建立了钢-混凝土组合梁桥跨越地裂缝的数值模型,研究地裂缝活动时钢-混组合梁桥的内力和变形特性。高欢[15]建立了云轨简支梁桥跨越活动地裂缝的数值模型,研究轨道梁、桥墩及桩基础的位移规律。

目前虽然在桥梁工程跨骑地裂缝的措施方面取得了一定成果,但研究主要集中在通过实例、模型试验或数值模拟分析高铁简支梁桥在地裂缝活动时的变形及内力情况,对于城市连续梁桥的研究则鲜见报道。高铁的路线通常在郊外,而连续梁桥多是在城市内部。西安地裂缝是典型的城市地质灾害,对城市地面沉降的影响尤为显著,因此本文以西安地裂缝活动为例,采用数值模拟的方法研究地裂缝活动对城市连续梁桥的影响作用,以期为跨地裂缝连续梁桥的合理设计提供参考。

1 有限元分析模型

西安地裂缝活动表现出三向特征,即同时竖向错动、水平张拉以及水平剪切，其中以竖向错动为主,通常表现为正断式特征,其上盘相对下盘沿地裂缝倾角下滑[2]。

当前桥梁跨骑地裂缝均采用简支梁结构,利用简支梁支座位移不产生内力的原理,减小地裂缝对桥梁的影响范围。采用这种结构虽然对箱梁的内力无显著影响,但是过大的沉降位移会使得箱梁与垫片的接触面积减小,从而造成梁的横向约束减低,存在安全隐患。如采用多跨连续梁跨骑地裂缝,地裂缝活动的影响范围虽然增大,但能够减小每一跨箱梁的倾斜,因此本文主要研究多跨连续梁跨骑地裂缝时的受力与变形响应机制。

模型工程原型为文献[14]中提到的雁塔路互通式立交桥中的三跨连续梁桥。利用MIDAS GTS NX建立该三跨连续梁桥正交跨骑地裂缝的有限元分析模型,如图1所示。模型长120 m、宽60 m,土层分为6层,厚度40 m,地裂缝正交于连续梁桥的正中心处,倾角80°。桥梁跨度均为32 m,桥墩高9 m、宽6 m,用垫板支撑上部箱梁。承台长10.4 m、宽7 m、高2 m,每个承台下设置4根30 m长的混凝土桩,单桩直径1 m。使用梁单元模拟混凝土桩,桩土之间的负摩阻力采用桩土接触单元模拟,桥墩、垫板、箱梁以及承台均采用实体单元模拟。混凝土预制箱梁宽12 m、高3.13 m,支撑垫板长1 m、宽1 m、高0.3 m。箱梁、桥墩、承台均采用C50混凝土。依据上述尺寸划分整体分析模型的网格,为了确保分析的精确度,加密群桩基础周围和地裂缝穿越处两侧网格单元。在模型中,X为轴向,Y为宽度方向,Z为竖向。本文研究内容为连续梁桥,与文献[18]所述不设缝管廊同为线性连续结构,对于地裂缝的模拟,二者采用了相同的方法,所以模型具有较高的可靠度。

图1 三跨连续梁桥正交跨越地裂缝分析模型Fig.1 Analysis model of a three-span continuous beam bridge orthogonally crossing ground fissure

1.1 材料本构模型及参数

土体材料采用莫尔-库仑模型,混凝土梁和钢垫板材料采用弹性模型。以西安实际地层为例,土体与桥梁结构材料的相关物理力学参数列于表1、表2[14]。

表1 土体材料物理力学参数Table 1 Physical and mechanical parameters of soil materials

表2 桥梁结构材料物理力学参数Table 2 Physical and mechanical parameters of bridge structural materials

1.2 边界条件及接触技术处理

在X、Y方向左右侧面及纵向两端面边界设置法向约束。在Z方向上,地层表面为自由面,地裂缝下盘底部设置竖向约束,上盘底部设置强制竖向位移,模拟地裂缝沉降情况。除地层模型整体边界条件外,考虑到群桩基础在Z方向上不能发生转动,还需设置桩单元边界条件。

箱梁与垫板之间、垫板与桥墩之间、桥墩与承台之间均采用interface接触单元模拟,设为刚性连接。地裂缝也采用interface接触单元模拟,可沿地裂缝倾角错动;地裂缝的接触单元法向刚度kn取8 000 kPa,切向刚度ks取800 kPa[16]。桩土接触单元参数列于表2。

1.3 计算工况

西安市当前地裂缝年活动速率为1～5 mm/a,桥梁的设计年限为100年,因此使用期限内地裂缝最大沉降量应按0.5 m考虑。为更精确地研究桥梁结构在地裂缝上盘不同沉降量下的变化情况,分别计算地裂缝上盘沉降量为0.1 m、0.2 m、0.3 m、0.4 m、0.5 m五种工况。

2 计算结果及分析讨论

2.1 箱梁位移和应力场分析

通过计算分别得到地裂缝上盘沉降量0.1 m、0.2 m、0.3 m、0.4 m、0.5 m五种工况下箱梁的竖向位移场云图。限于篇幅,仅以沉降量0.5 m工况下的结果来进行分析(图2)。由图2可见,箱梁的竖向位移从下盘至上盘逐渐增加,整个竖向位移场云图可以分为3段:下盘边跨的微抬升稳定变形区、地裂缝处中间跨的强差异沉降变形区,以及上盘边跨的强沉降稳定变形区。两边跨虽然沉降位移的数值相差较大,且下盘边跨抬升而上盘边跨下沉,但相邻点的沉降差较小,均属变形稳定区域;中间跨相邻点的沉降差较大,属强差异沉降区域。

图2 沉降量为0.5 m时箱梁竖向位移场云图Fig.2 Contour of vertical displacement field of box girder under settlement of 0.5 m

为对比地裂缝不同沉降量下箱梁的竖向与水平位移,需取同一位置的位移量进行分析。由于箱梁的横向刚度较大,横截面各点处位移相近,所以取箱梁结构顶部中轴处的结果来进行分析,其竖向位移与水平纵向位移曲线变化如图3所示。由图3(a)可见,不同地裂缝沉降量影响下,地裂缝正交桥梁处的中间跨均为箱梁结构竖向位移的主要差异沉降区。不同沉降量下箱梁的主要差异沉降区范围接近,均在上下盘各20 m长、共计40 m的区域,可认为这是地裂缝的影响带宽度。分析其原因,地裂缝的沉降使得上盘的桥墩产生向下的竖向位移,而下盘的桥墩几乎不发生位移,由于箱梁的刚度较大,不同的桥墩位移可以看作是不同的支座位移,使得多跨梁的内力重新分布。箱梁变形主要表现为上盘一侧下沉而下盘边跨轻微抬升,地裂缝下沉量越大,抬升变形就越大,箱梁结构的竖向变形均呈反“S”形。

由图3(b)可见,箱梁结构的水平纵向位移量随着地裂缝沉降量的增加几乎呈等间距增大。当沉降量为0.1 m时,箱梁最大水平纵向位移为2.45 cm;当沉降量为0.5 m时,箱梁最大水平纵向位移为11.09 cm。同时,不同地裂缝活动程度下箱梁的水平位移均为正值,表明箱梁整体向上盘方向移动,且沉降量越大,箱梁的水平位移越不均匀。

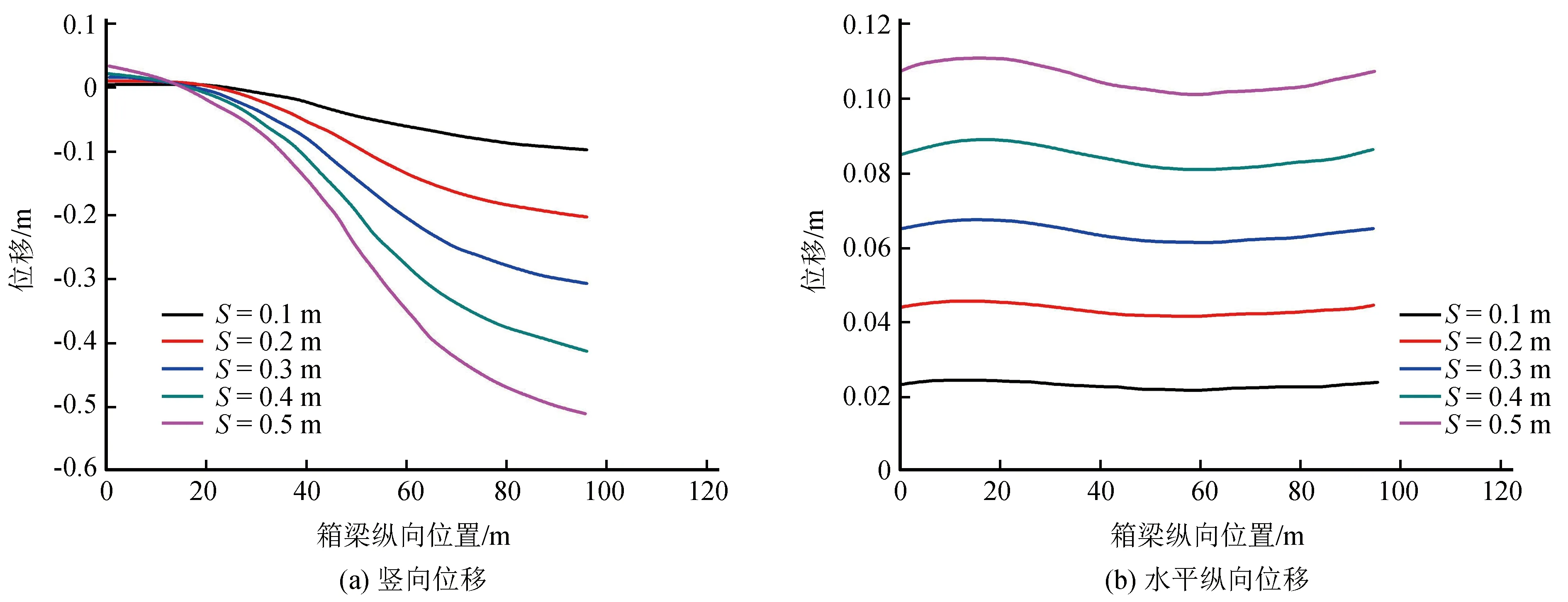
图3 不同沉降量下箱梁顶部中轴处竖向与水平纵向位移变化曲线Fig.3 Vertical and horizontal displacement curves at the central axis of the top of box girder under different settlement

各跨箱梁在不同竖向沉降量下的倾斜度如图4所示。跨越地裂缝的中跨箱梁倾斜度最大,当沉降量为0.5 m时倾斜度为0.97%;右边跨箱梁倾斜度次之,当沉降量为0.5 m时倾斜度为0.42%;左边跨箱梁倾斜度最小,当沉降量为0.5 m时倾斜度为0.34%。《公路桥涵地基与基础设计规范(JTG D63—2007)》[17]规定:相邻墩台间的不均匀沉降差值不应使桥面形成大于0.2%的附加纵坡。当地裂缝竖向沉降量为0.1 m时,桥梁各跨均满足规范要求;沉降量达到0.2 m时,中跨倾斜度超过规范限值。跨度相同的32 m简支梁,0.2%的倾斜角对应的允许最大不均匀沉降量仅为6.4 cm,可见采用多跨梁一定程度上可以提高梁适应不均匀沉降的能力。

图4 箱梁在不同沉降量下的倾斜度Fig.4 Inclination of box girder under different settlement

地裂缝活动对箱梁内力的影响主要以弯矩产生的横截面上的纵向应力为主,本文分析了0.1 m、0.2 m、0.3 m、0.4 m、0.5 m 五种沉降量工况,其中沉降量0.5 m时的箱梁纵向应力云图如图5所示。由图可见,箱梁上下表面纵向应力方向相反,上下盘纵向应力方向呈反对称分布,峰值区域位于靠近地裂缝的两个桥墩处,大致为上盘上表面受压、下表面受拉,下盘上表面受拉、下表面受压。拉力的峰值略大于压力峰值,其原因可能在于地裂缝的倾斜下沉活动存在水平张拉作用,使得箱梁产生附加纵向拉力,与竖向作用下的纵向拉力叠加,最终使得拉力大于压力。

图5 沉降量为0.5 m时箱梁水平纵向应力场云图Fig.5 Contour of horizontal stress field of box girder under settlement of 0.5 m

不同沉降量下箱梁结构上下中轴处的纵向应力如图6所示。随着沉降量的增加,箱梁纵向应力不断增加,且下表面纵向应力的数值均略高于上表面。根据《混凝土结构设计规范(GB50010—2011)》的规定:C50混凝土极限拉应变εt=0.000 1,极限压应变εc=0.003 3,通过公式σ=Eε,计算得混凝土极限拉应力为5 000 kN。可见,当地裂缝活动沉降量大于0.1 m时,箱梁混凝土发生受拉破坏。

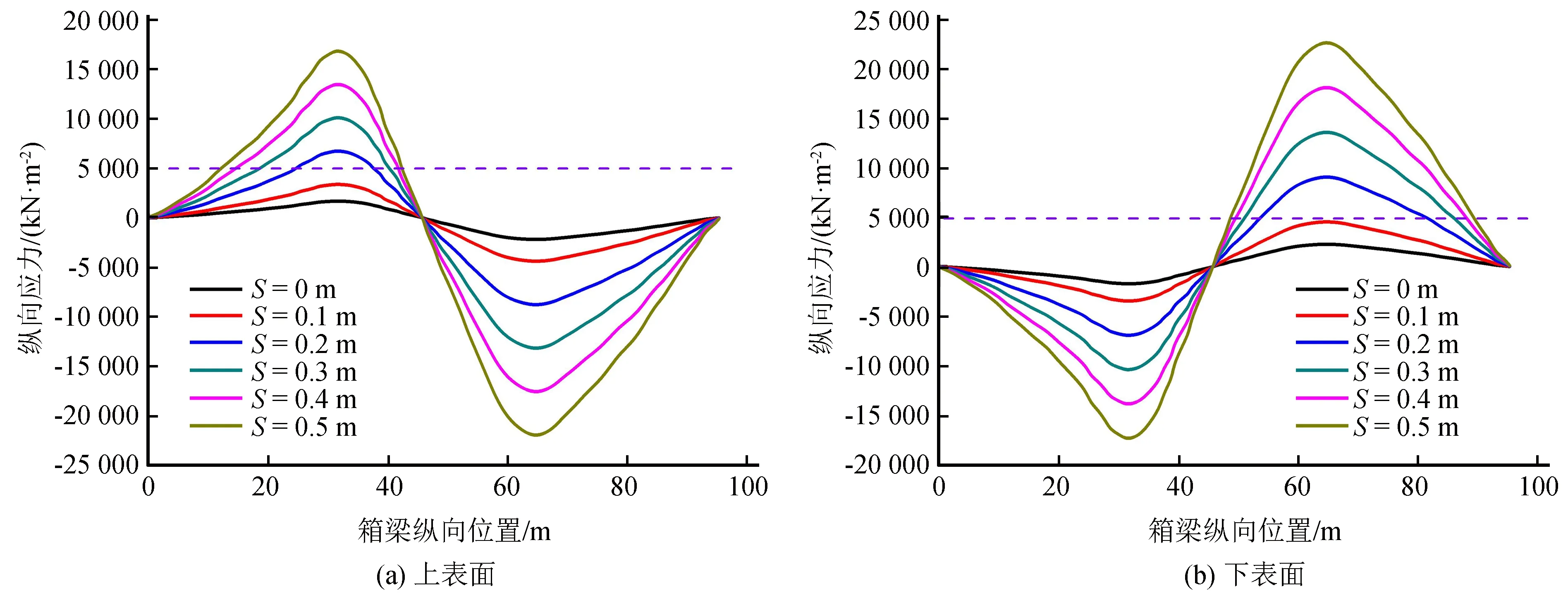
图6 不同沉降量下箱梁上下表面中轴处纵向应力对比Fig.6 Comparisonbetween longitudinal stress on the central axis of the upper and lower surfaces of box girder under different settlement

2.2 墩台位移场分析

墩台结构是桥梁整体性结构的另一个主要组成部分,地裂缝不同沉降量下墩台结构中轴处的竖向位移与水平纵向位移如图7所示。可见,随着地裂缝活动程度的增加,墩台的竖向与水平位移均不断增加,且竖向的不均匀沉降越来越显著。

图7 不同沉降量下墩台表面中轴处竖向与水平纵向位移变化曲线Fig.7 Vertical and horizontal displacement curves at the central axis of pier surface under different settlement

将墩台从下盘向上盘依次编号,各桥墩在不同沉降量下的倾斜度如图8所示。可见位于地裂缝下盘的2号桥墩的倾斜度最大,当沉降量为0.5 m时倾斜度为0.69%;位于下盘的1号桥墩次之,当沉降量为0.5 m时倾斜度为0.58%;位于上盘的4号桥墩,当沉降量为0.5 m时倾斜度为0.48%;位于上盘的3号桥墩的倾斜度最小,当沉降量为0.5 m时倾斜度为0.37%。

图8 桥墩在不同沉降量下的倾斜度Fig.8 The degree of inclination of pier under different settlement

《公路桥涵地基与基础设计规范(JTG D63—2007)》[17]规定:墩台倾斜不得超过0.2%，因此当地裂缝竖向沉降超过0.1 m时,墩台的倾斜已超过规范要求。

综上可知,若采用相同跨度简支梁跨越活动地裂缝,其允许沉降量为6.4 cm,而采用三跨连续梁,虽然地裂缝活动的影响范围增加,但其适应地裂缝活动的能力得到提高,当地裂缝沉降0.1 m时,箱梁的倾角、纵向应力以及墩台的倾斜均能满足规范要求。这表明跨越活动性微弱的地裂缝时,多跨梁可以更好地满足规范要求,对地层不均匀沉降的适应性较好。

3 结论

基于MIDAS GTS NX开展了地裂缝活动对三跨连续梁桥作用的力学分析,模拟了地裂缝上盘不同沉降量条件下桥梁结构的变形破坏情况,并分析了地裂缝上盘不同沉降量条件下箱梁及墩台的位移场和应力场及其变化曲线,得到以下结论:

(1) 箱梁的变形可以分为三段:微抬升区、不均匀差异沉降区和整体稳定沉降区。跨骑地裂缝的中间跨为三跨连续箱梁结构在不同沉降量条件下的主要差异沉降区,其影响带宽度大致等同,均为上下盘各20 m长、共计40 m的区域;

(2) 当地裂缝沉降量达到0.1 m时,多跨梁的各跨倾斜仍能满足规范要求,其适应变形能力优于单跨梁;

(3) 地裂缝活动下箱梁破坏时的峰值应力出现在箱梁下表面上盘靠近地裂缝的桥墩处,当地裂缝沉降量达到0.1 m时,多跨梁的整体轴向应力均能满足规范要求,当地裂缝沉降量超过0.1 m时,箱梁可能发生破坏。可以对桥墩沉降量和主梁内力进行监测,并在连续梁桥的墩台位置设置可调节的升降式支座,当监测到桥墩出现较大的沉降量时,可通过调节支座高度减小桥墩之间的相对沉降量,改善梁的受力状态;

(4) 各桥墩在不同沉降量下的倾斜度以位于地裂缝下盘的2号桥墩最大,且当地裂缝沉降量未达到0.1 m时,所有墩台倾斜均能满足规范要求;

(5) 连续梁桥跨越活动性微弱的地裂缝时,多跨梁对地层不均匀沉降有更好的适应性。