循环荷载下不锈钢力学性能建模方法

孙治国,杨葆洋,张震威,王东升

(1.防灾科技学院中国地震局建筑物破坏机理与防御重点实验室,北京 101601;2.河北工业大学土木与交通学院,天津 300401)

0 引言

不锈钢有着外型美观、耐腐蚀、易于维护和较低的生命周期成本等诸多优点,近年来在土木工程中的应用越来越广泛[1-2]。不锈钢是根据合金中铬的含量来进行分类的,在结构工程中常用的不锈钢主要包含奥氏体和双相型两种类型。其中,奥氏体不锈钢具有优良的延展性、耐火性和非磁性[3];双相型不锈钢具有高强度、优良的抗腐蚀性和可焊性[4]。

强震发生时,结构的不锈钢构件(尤其是耗能元件)将承受低周疲劳荷载作用,准确认识不锈钢材料的滞回本构模型是研究不锈钢结构抗震性能的前提[5-7]。近年来,国内外学者对不锈钢材料进行了相关试验研究与数值分析。朱浩川等[8]通过ABAQUS软件模拟了双相型不锈钢2205简支薄板纵向受压试验,模拟结果验证了模型的准确性与实用性。王元清等[9]对奥氏体不锈钢S31608试件开展了不同模式下的循环加载试验与数值模拟,研究发现,在循环荷载下试件的滞回曲线饱满,在循环加载后期应力有显著提高。王萌等[10]利用 ABAQUS软件,考虑了不锈钢循环强化作用,提出了奥氏体不锈钢单轴滞回本构模型(骨架准则和滞回准则)。Zhou等[11]对奥氏体不锈钢304和双相型不锈钢LDX2101两种材料的滞回性能进行了研究,通过试验发现,两种不锈钢材料的滞回曲线稳定、饱满,且拥有良好的塑性变形能力。Zhou等[12]进一步研究了不锈钢筋的低周疲劳性能和变形能力,对奥氏体不锈钢316LN,双相型不锈钢2205等进行了试验,研究发现,不锈钢筋比普通碳素钢筋具有更好的延性,且疲劳寿命更长。

为了完成地震作用下不锈钢构件受力性能的模拟分析,同时考虑到OpenSees数值分析平台在结构抗震分析中的广泛应用,有必要讨论基于OpenSees数值分析平台的不锈钢力学性能建模方法,从而为含不锈钢的工程结构的抗震分析与设计提供依据。

本文研究内容主要有以下两个方面:一是开展了奥氏体不锈钢及双相型不锈钢在循环加载下的应力-应变滞回曲线模拟,讨论了奥氏体不锈钢S31608在5种循环加载制度下,双相型不锈钢LDX2101在3种加载制度下和双相型不锈钢S22053在4种加载制度下应力-应变关系的数值模拟方法,并给出了建模的相关建议。二是在此基础上,模拟了配置奥氏体不锈钢筋的节段拼装桥墩滞回性能,进一步验证了不锈钢力学性能数值建模方法的准确性。

1 不锈钢力学性能试验介绍

1.1 奥氏体不锈钢S31608试验介绍

参考王元清等[9]完成的试验结果,对奥氏体不锈钢S31608的滞回性能进行模拟。试件尺寸如图1所示,试件为扁平截面,试验段有效长度(20 mm)与截面高度(14 mm)之比为1.43。本文选择A1～A6等6个试件进行模拟。其中,A1试件单调拉伸,A2～A6试件循环加载,加载制度按应变ε控制,A2、A3、A5为循环上升加载(应变ε逐级增加),A4为等辐循环加载(应变ε=0.4%),A6为循环下降加载(应变ε逐级减小)。

图1 文献[9]中试件的设计情况(单位:mm)Fig.1 Design details of the specimens in reference [9](Unit:mm)

1.2 双相型不锈钢LDX2101试验介绍

参考Zhou等[11]完成的试验结果,对双相型不锈钢(LDX2101)的滞回性能进行了模拟。试验中分别采用热轧和冷轧两种加工工艺,热轧板试件(HR2101)和冷轧板试件(CR2101)的力学性能如表1所列。HR2101为圆形截面,试验段有效长度(15 mm)与直径(10 mm)的比值为1.5;CR2101为扁平截面,试验段有效长度(13 mm)与截面高度(12.5 mm)之比为1.04,如图2所示。两种试件在循环上升加载、循环交替加载及循环拉伸加载3种模式下进行加载。

表1 双相型不锈钢力学性能Table 1 Mechanical properties of the duplex stainless steel

图2 文献[11] 中双相型不锈钢试件(单位:mm)Fig.2 Duplex stainless steel specimens in reference [11](Unit:mm)

1.3 双相型不锈钢S22053试验介绍

参考骆晶等[13]完成的试验结果,对双相型不锈钢S22053的滞回性能进行模拟。试件尺寸如图3所示,试验段有效长度(15 mm)与截面高度(10 mm)之比为1.5。本文选择a-3、a-4、a-5、a-6等4个试件进行模拟。其中,a-3、a-4为循环上升加载,a-5、a-6为等辐循环加载。

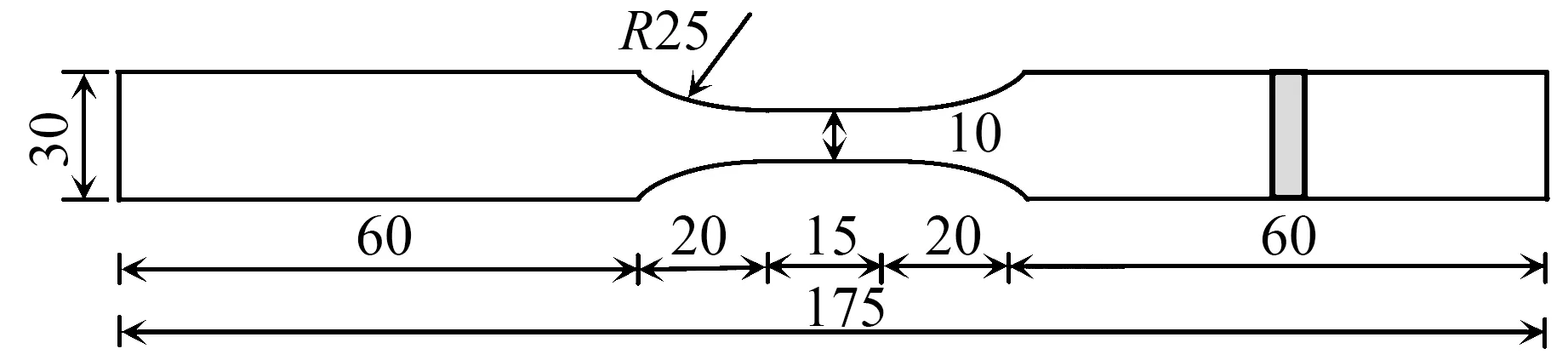
图3 文献[13] 中的双相型不锈钢试件(单位:mm)Fig.3 Duplex stainless steel specimens in reference [13](Unit:mm)

2 不锈钢力学性能建模方法

图4为不锈钢筋与碳素钢筋受拉应力-应变关系对比情况。可以发现,不锈钢筋的应力-应变曲线弹性阶段到塑性阶段平滑过渡,无明显的屈服点及屈服平台,因此一般取卸载时产生的塑性应变为0.2%时对应的应力作为不锈钢材料的名义屈服强度。

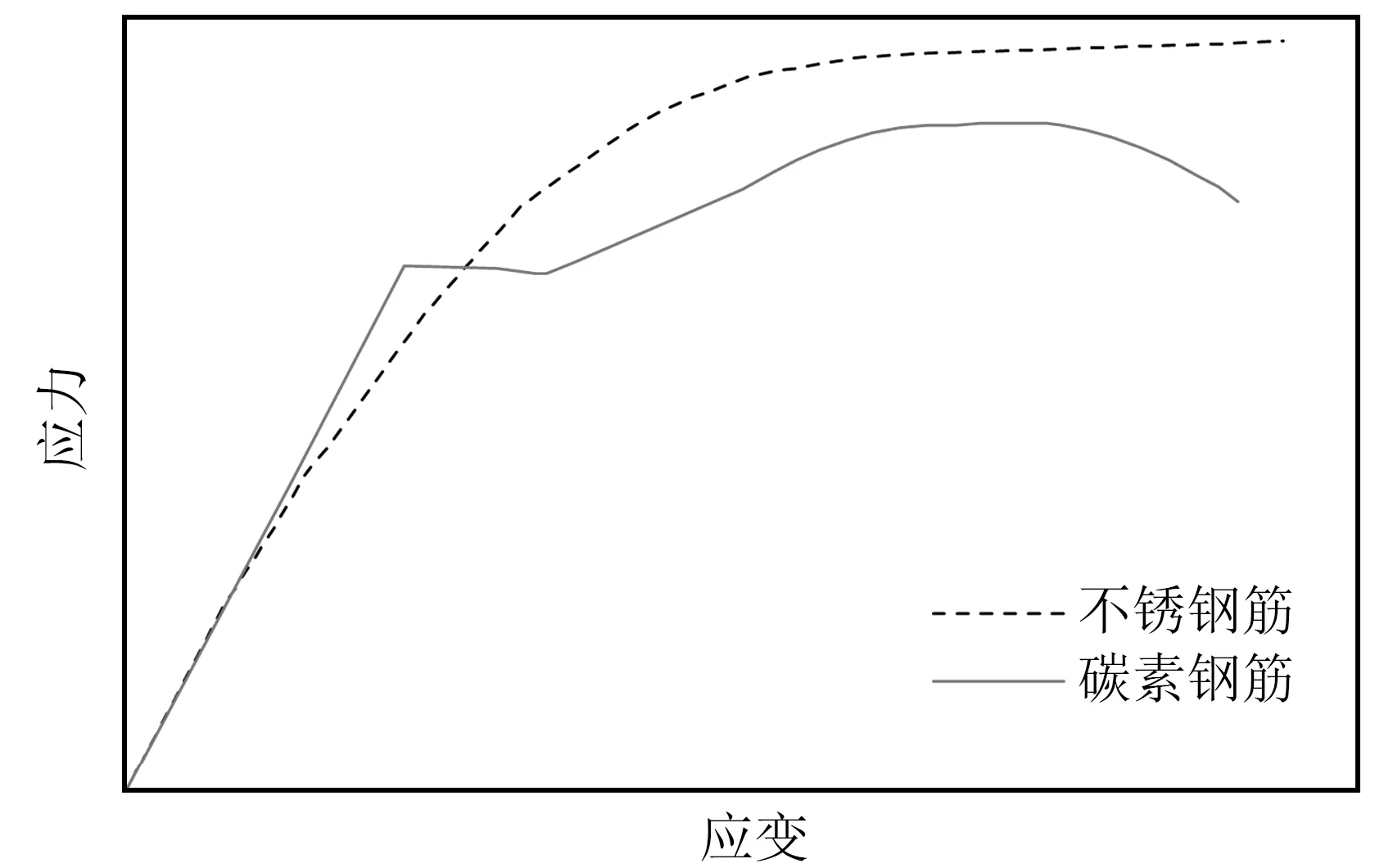
图4 不锈钢筋与碳素钢筋应力-应变对比Fig.4 Comparison between stress-strain curves of stainless steel and carbon steel bars

不锈钢筋的本构关系与碳素钢筋不同,不再满足理想的弹塑性模型[14]。经典的不锈钢筋的本构关系是由Ramberg和Osgood提出,Hill对其进行了修正,该模型的应力σ-应变ε关系可以表达为:

(1)

式中:fy为钢筋名义屈服强度;k为应变硬化指数;E0为材料弹性模量;a为屈服时残余应变,一般取0.002。

图5为OpenSees数值分析平台中Ramberg-Osgood steel材料模型循环加载下的滞回规则。材料屈服后,随着循环次数的增加,循环硬化出现。不同应变幅下循环硬化程度R可表达为:

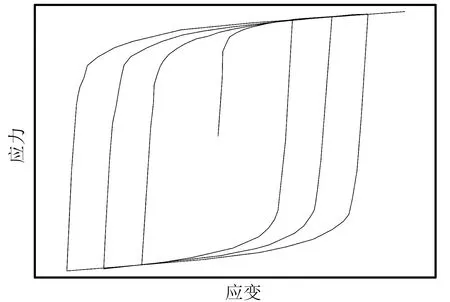
图5 Ramberg-Osgood steel材料模型的滞回规则Fig.5 Hysteretic behavior of Ramberg-Osgood steel material model

(2)

2.1 奥氏体不锈钢S31608模型建立

不锈钢本构模型选用OpenSees数值分析平台中的Ramberg-Osgood steel材料模型,模型中主要参数有fy、E0、a和n。其中,n为控制材料从弹性阶段到塑性阶段过渡的参数。

图6为奥氏体不锈钢不同“n”取值时模拟结果对比。其中,试验结果为王元清等[9]完成的奥氏体不锈钢S31608试件(试件A1与A2)。可以发现随着n值增大,模拟得到的不锈钢的强化速率随之降低;在单调加载作用下,n值取10时模拟与试验结果吻合最佳;在循环荷载作用下,n值取5时模拟与试验结果吻合最佳。

图6 奥氏体不锈钢S31608不同“n”取值模拟结果对比Fig.6 Comparison between simulation results of austenitic stainless steel S31608 with different values of "n"

2.2 双相型不锈钢LDX2101模型建立

双相型不锈钢采用Ramberg-Osgood steel材料模型,图7为双相型不锈钢不同“n”取值时模拟结果与Zhou等[11]完成的HR2101试件试验结果的对比。

图7 双相型不锈钢LDX2101不同“n”取值模拟结果对比Fig.7 Comparison between simulation results of duplex stainless steel LDX2101 with different values of "n"

可以看出:在循环上升和循环交替加载制度下,n值取5时模拟结果与试验结果吻合最佳;在循环拉伸加载制度下,n值取12时模拟结果与试验结果吻合最佳。

2.3 双相型不锈钢S22053模型建立

双相型不锈钢S22053仍采用Ramberg-Osgood steel材料模型,图8为双相型不锈钢不同“n”取值时模拟结果与骆晶等[13]完成的S22053试件试验结果的对比。从图中可以看出,在等幅循环加载作用下,n值取5时模拟与试验结果吻合最佳。

图8 双相型不锈钢S22053不同“n”取值模拟结果对比Fig.8 Comparison between simulation results of duplex stainless steel S22053 with different values of "n"

3 模拟结果与分析

3.1 奥氏体不锈钢S31608试件模拟结果

A1试件为王元清等[9]完成的奥氏体不锈钢单调加载试件,模拟时n值取10,其模拟结果如图9(a)所示,模拟结果与试验结果吻合较好,模型能够较准确地描述奥氏体不锈钢S31608在单调荷载作用下的受力特征。

图9(b)～(f)为王元清等完成的奥氏体不锈钢循环加载模拟结果与试验结果对比,模拟时n值取5。

图9 奥氏体不锈钢S31608模拟与试验结果对比Fig.9 Comparison between simulation and experimental results of austenitic stainless steel S31608

可以看出,所建模型模拟得到的奥氏体不锈钢滞回曲线与试验结果吻合良好,说明Ramberg-Osgood steel材料本构能够描述奥氏体不锈钢S31608材料在不同循环加载方式下的响应。材料屈服后,随着循环次数的增加,循环硬化出现,循环后期应力明显提高[15]。

3.2 双相型不锈钢LDX2101试件模拟结果

图10为双相型不锈钢(LDX2101材料)数值模拟结果与Zhou等[11]完成的试验结果对比图,其中,试件HR2101-a和试件CR2101-a为循环上升加载试件,试件HR2101-b和试件CR2101-b循环交替加载试件,以上两种加载制度在模拟时n值取值均为5;试件HR2101-c 和试件CR2101-c为循环上升加载试件,模拟时n值取12。模拟得到的滞回曲线与试验结果吻合良好,Ramberg-Osgood steel材料本构能够较准确地描述双相型不锈钢LDX2101材料在循环荷载作用下的受力特征。

图10 双相型不锈钢LDX2101循环加载模拟与试验结果对比Fig.10 Comparison between simulation and experimental results of duplex stainless steel LDX2101

3.3 双相型不锈钢S22053试件模拟结果

图11为双相型不锈钢S22053试件数值模拟结果与骆晶等[13]完成的试验结果对比图。在四种循环加载制度下,模拟时n值取值均为5。模拟得到的滞回曲线与试验结果吻合良好,Ramberg-Osgood steel材料本构能够较准确地描述双相型不锈钢S22053材料在循环荷载作用下的受力特征。等辐循环加载时,试件a-6在相同应变下的应力随着循环次数的增加而增大,而后趋于稳定,材料表现出典型的循环硬化效应。

图11 双相型不锈钢S22053循环加载模拟与试验结果对比Fig.11 Comparison between simulation and experimental results of duplex stainless steel S22053

综上所述,采用Ramberg-Osgood steel材料本构分别对奥氏体不锈钢和双相型不锈钢两种类型的多个试件进行了不同加载方式下的模拟计算,与试验结果进行对比,结果均吻合良好,说明Ramberg-Osgood steel材料本构模型可以较好地模拟不锈钢材料在循环荷载下的应力-应变滞回反应。

4 桥墩有限元模拟及验证

上述研究表明,Ramberg-Osgood steel材料模型可以较准确地模拟不锈钢材料力学性能,为了进一步验证该模型在桥墩抗震有限元模型中的可靠性,对Ou等[16]完成的配置不锈钢筋的节段拼装桥墩试件C5C-E32的拟静力试验结果进行模拟。桥墩中的耗能钢筋为奥氏体不锈钢Enduramet 32材料,名义屈服强度为580 MPa,极限强度为939 MPa。其余配筋为普通钢筋。桥墩为矩形空心截面,试验采用拟静力加载,在墩顶侧向加载位移角分别为0.25%、0.375%、0.5%、0.75%、1.0%、1.5%、2.0%、3.0%、4.0%和5%,每个加载位移下循环2次。

本节介绍了耗能钢筋配置不锈钢筋的桥墩建模方法,耗能钢筋配置普通钢筋的桥墩建模细节可参考文献[17] 。

桥墩试件中的混凝土材料模型选用Concrete01材料模型,普通纵筋选用Steel02材料模型,预应力筋采用Elastic-PP材料模型。耗能钢筋采用Ramberg-Osgood steel材料模型,n取值为5。在桥墩墩底摇摆接缝处布置了5个零长度单元,并配合Elastic-No Tension单压材料进行模拟,材料受压刚度E取值为[18]:

(3)

式中:A为桥墩混凝土截面面积;Ec为受压混凝土弹性模量;m为模拟接缝处反应的零长度单元个数;L为桥墩墩高;θ为经验系数。

图12为桥墩的数值分析模型。桥墩的重力荷载施加在墩顶,墩身采用纤维梁柱单元模拟,墩身分为两部分建模,墩身上部为无耗能钢筋的截面,墩身下部为有耗能钢筋的截面。无黏结预应力筋与耗能钢筋均采用truss单元模拟,同时预应力筋与墩身、耗能钢筋与墩身均采用刚性单元进行连接,以保证与墩身协同变形。

图12 配置不锈钢筋的空心墩数值分析模型Fig.12 Numerical analysis model for the hollow pier with stainless steel bars

图13为模拟及试验得到的试件墩顶侧向承载力-位移角滞回曲线。可以看出,模拟得到的试件刚度、承载力等与试验结果基本吻合。

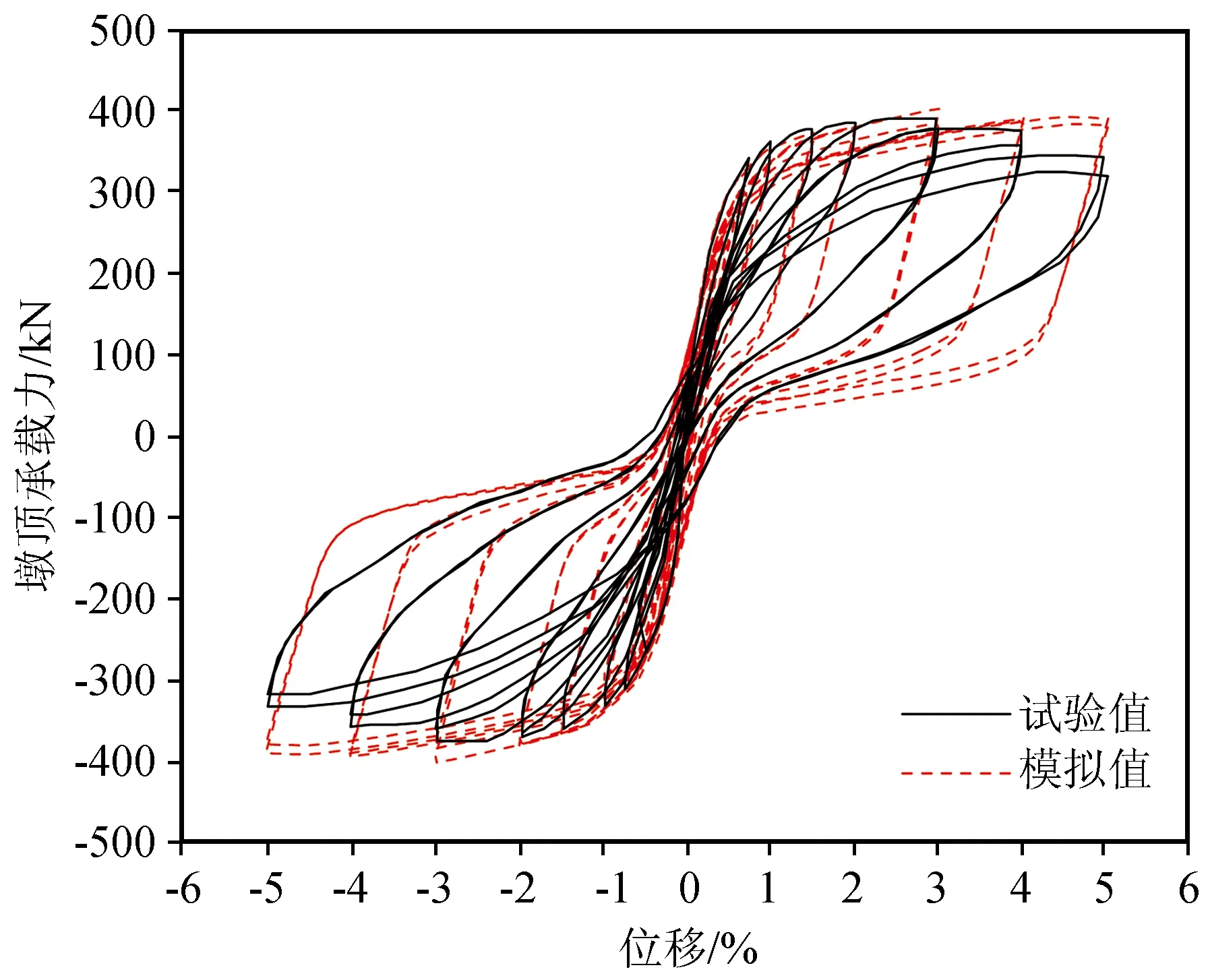
图13 承载力-墩顶位移角滞回曲线Fig.13 The hysteretic curves of bearing capacity-drift ratio at the pier top

模拟得到的墩底接缝宽度是通过提取桥墩最外侧只受压弹簧的变形。模拟得到的墩底接缝宽度-墩顶位移角及与试验结果对比如图14所示。墩底接缝宽度范围为-10 ～35 mm,模拟结果与试验结果吻合良好。

图14 墩底接缝宽度-墩顶位移角Fig.14 Connection width at pier bottom-drift ratio at pier top

图15为模拟及试验得到的试件预应力筋拉力-墩顶位移角关系图。在循环加载过程中,模拟得到的预应力拉力比试验中实际预应力筋拉力偏大,这可能是因为模型不能准确模拟预应力筋应力损失所致。

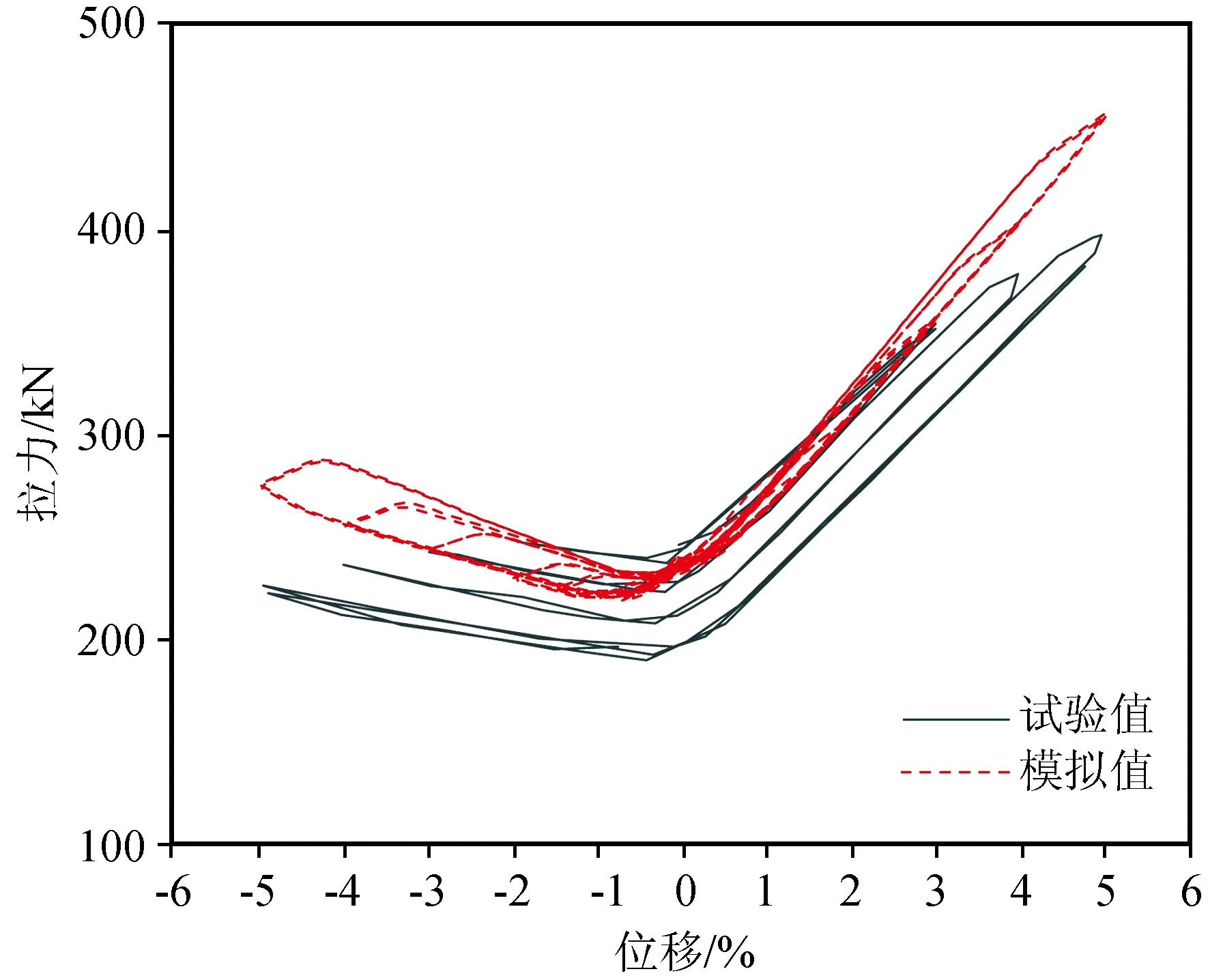
图15 预应力筋拉力-墩顶位移角Fig.15 Tensile force in prestressed tendon-drift ratio at pier top

残余位移是指当水平力为0时,墩顶未恢复的变形,通过提取滞回曲线与横坐标交点处的位移可得。图16为试件残余位移角-墩顶位移角关系图。

图16 残余位移角-墩顶位移角Fig.16 Residual drift ratio-drift ratio at pier top

综上所述,节段拼装桥墩有限元模型基本可以模拟桥墩的真实滞回反应,验证了建模方法的可靠性,建模时不锈钢筋所取参数合理。

5 结论

基于OpenSees数值分析平台,通过不锈钢材料和配置不锈钢筋的桥墩试件两个层次,讨论了循环荷载作用下不锈钢筋力学性能建模方法,得出以下结论:

(1) 通过采用Ramberg-Osgood steel材料模型,建立不锈钢材料力学性能数值分析模型,模拟得到的应力-应变曲线符合不锈钢滞回本构特点,Ramberg-Osgood steel材料模型可用于不锈钢力学性能分析。

(2) 分别模拟了奥氏体不锈钢和双相型不锈钢两种类型材料的滞回曲线,将模拟结果与不同循环加载试验结果进行对比,发现所建模型能够较好地对不锈钢材料的滞回曲线进行拟合,可以预测不锈钢在不同加载方式下的响应。

(3) 模拟过程中,当控制材料从弹性到塑性阶段过度的参数n值增大时,材料的强化速率会随之降低。由于不锈钢材料在单调加载下的受力性能与循环加载下有较大区别,数值建模时n值要分别取值。

(4) 对配置不锈钢筋的节段拼装桥墩拟静力试验进行了模拟,模拟结果与试验结果吻合较好,所建模型可用于模拟配置不锈钢筋的节段拼装桥墩滞回反应。