长短周期地震波作用下钢框架结构的响应特性对比分析

孙鸿玲,胥 彬,刘秋林

(西南石油大学 土木工程与测绘学院,四川 成都 610500)

0 引言

基于1971年2月9日在美国发生的San Fernando地震动记录数据,Hanks最早于1975年提出了“长周期地震动”一词[1]。历史上最早于1968年5月16日在Tokachi-Oki地震中记录到了长周期地震动。直到1985年9月19日发生的Michoacan地震(8.1级)中出现高层建筑的严重震害,才使人们真正意识到长周期地震动的危害性与短周期地震动有着明显不同[2]。地震发生后,地震动经由远距离传播,到达深厚覆盖层场地上时,由于覆盖层的放大、滤波作用,形成长周期地震动。长周期地震动具有幅值低、持时长、低频成分丰富、卓越周期从几秒到几十秒这些特点,使得长周期建筑结构容易产生“类共振”效应,从而导致严重的震害。

1996年11月9日,黄海发生6.1级地震,震中160 km外的上海市区并无房屋倒塌和人员伤亡,但东方明珠顶部发生破坏,导致5根玻璃钢消雷器跌落[3]。2008年5月12日在四川省汶川县发生8.0级地震,震中40 km外的都江堰市和90 km外的成都市高层建筑损坏较轻,然而400 km外汉中市一栋高层建筑出现了较大的楼顶位移,绝大部分填充墙发生较严重的损坏[4],500 km外西安市一座100多米高的钢筋混凝土烟囱垮了一半[5]。2017年8月8日在四川九寨沟发生7.0级地震,距离震中490 km的西安市内高层建筑出现了长时间的剧烈晃动,引起了人员恐慌。

这说明地震动经过远距离传播后,会对特殊场地上的高层、超高层建筑产生更为严重的破坏。上述场地中,上海地区属于滨海相沉积型天然软基;汉中、西安地处渭河盆地,以黄土和砂砾石为主;西安市位于南部凹陷区,沉积物厚度300 m左右。

与此同时,我国许多大中型城市位于沉积盆地之中或附近,包括北京、西安、昆明、成都、兰州等,而上海等城市位于冲积平原之上。这些城市的高层钢结构建筑数量较多,且位于盆地或深厚软土场地上,属于长周期地震动的潜发区域。目前,针对长周期地震动与短周期地震动的区别,相关验算和设计规范的研究还在初级阶段。根据国内外长周期震害史来看,对于某些地区的高层建筑,进行长、短周期地震动的差异化分析是有必要的。

基于此,本文收集了10条典型的长周期地震动记录和10条短周期地震动记录,分析长周期地震动相较于短周期地震动的频谱特征差异,并对一栋20层的钢框架结构进行非线性时程分析,根据计算结果对比分析高层钢框架结构在长、短周期地震动作用下的响应差异。

1 长、短周期地震动的特性差异

日本研究长周期地震动较早,拥有大量的长周期震害资料。根据已有的研究成果和地质结构资料,日本地震调查研究推进总部通过数值模拟预测了可能出现长周期地震动的幅值、频谱、持时三要素,于2009年颁布了《长周期地震动预测地图》[6]。本文采用日本相关部门JMA(国土交通省气象厅)对长周期地震动的判定方法:在自振周期[1.6 s,7.8 s]内,绝对速度反应谱Sva(ξ=5%)峰值≥5 cm/s时被认定为长周期地震动[7]。

本文从日本KiK-net和K-NET台网中选取2003年Tokachi(8.0级)、2011年East Japan(9.0级)以及2016年Kumamoto(7.4级)三次地震中10条典型的长周期地震动记录以及10条国内外的短周期地震动记录作为时程分析中输入的地震动。对原始长周期地震动采用线性多项式类型进行基线校正的调整处理;采用Butterworth数字滤波器,选用4阶高通滤波类型,以截止频率为0.03 Hz进行滤波处理。处理之后地震动的各项特性参数如表1、2所列。

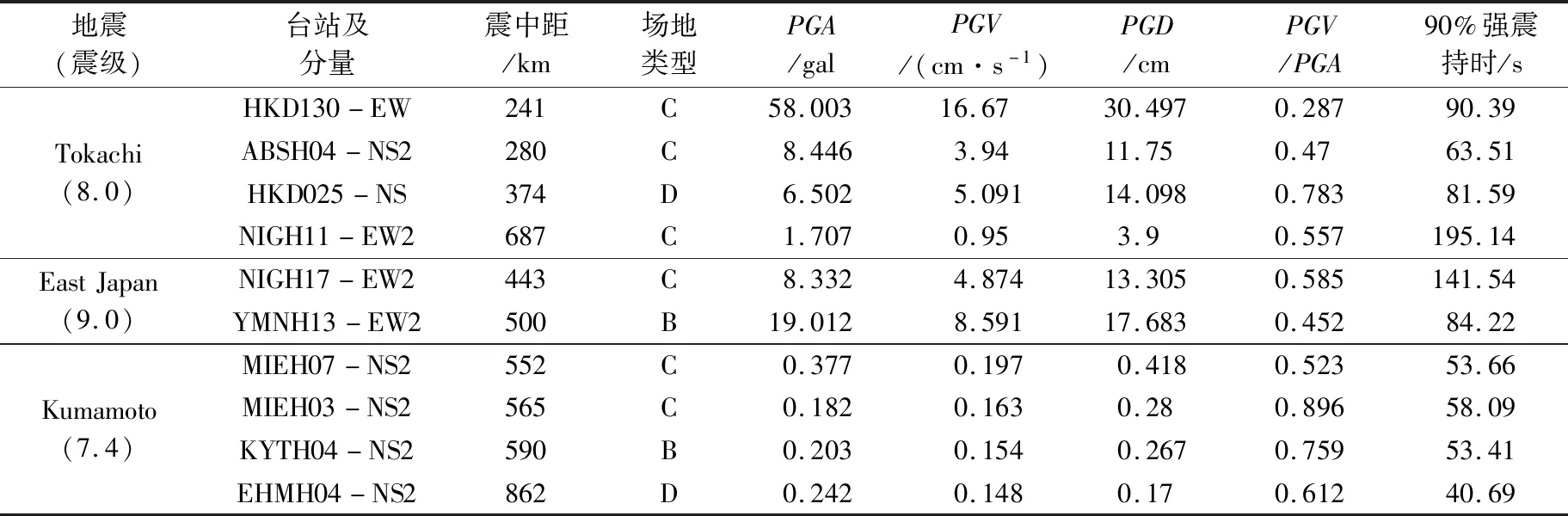
表1 长周期地震动的特性参数Table 1 Characteristic parameters of long-period ground motions

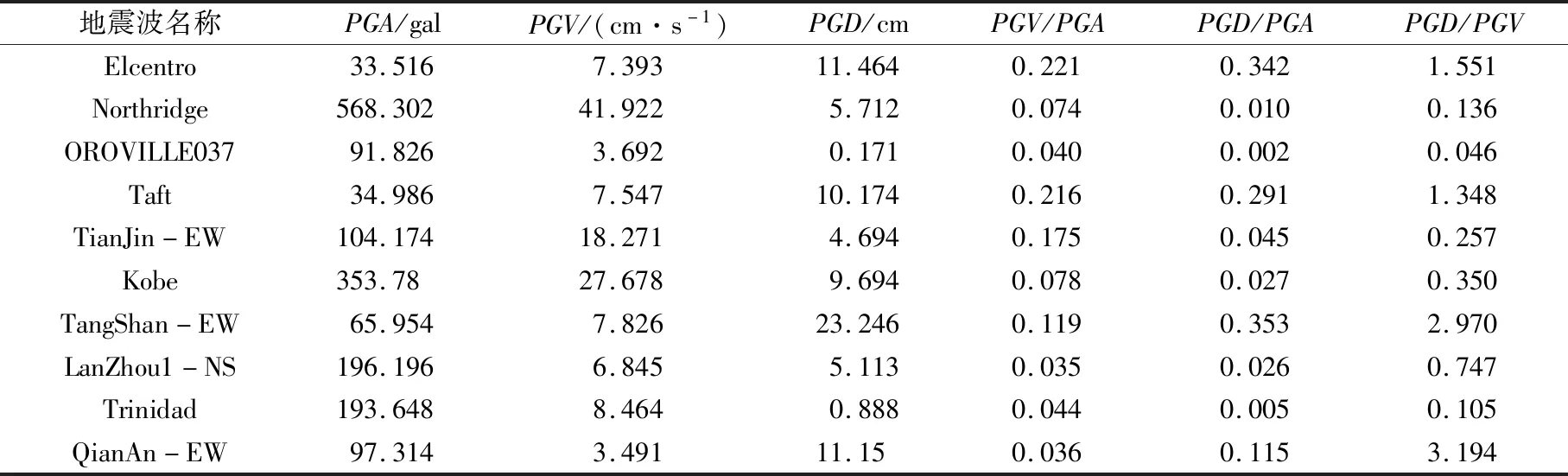
表2 短周期地震动的特性参数Table 2 Characteristic parameters of short-period ground motions

考虑到地震波传递到基岩时,其强度已经大量衰减,在传递到深厚覆盖软土层后向上传播的过程中,软土场地的滤波效应(低频放大、高频衰减)会导致其强度、频谱特性以及持时发生显著改变,使长周期成分增多。在这种前提下,进一步分析长周期地震动与短周期地震动的时程峰值及峰值比差异,结果如图1所示。

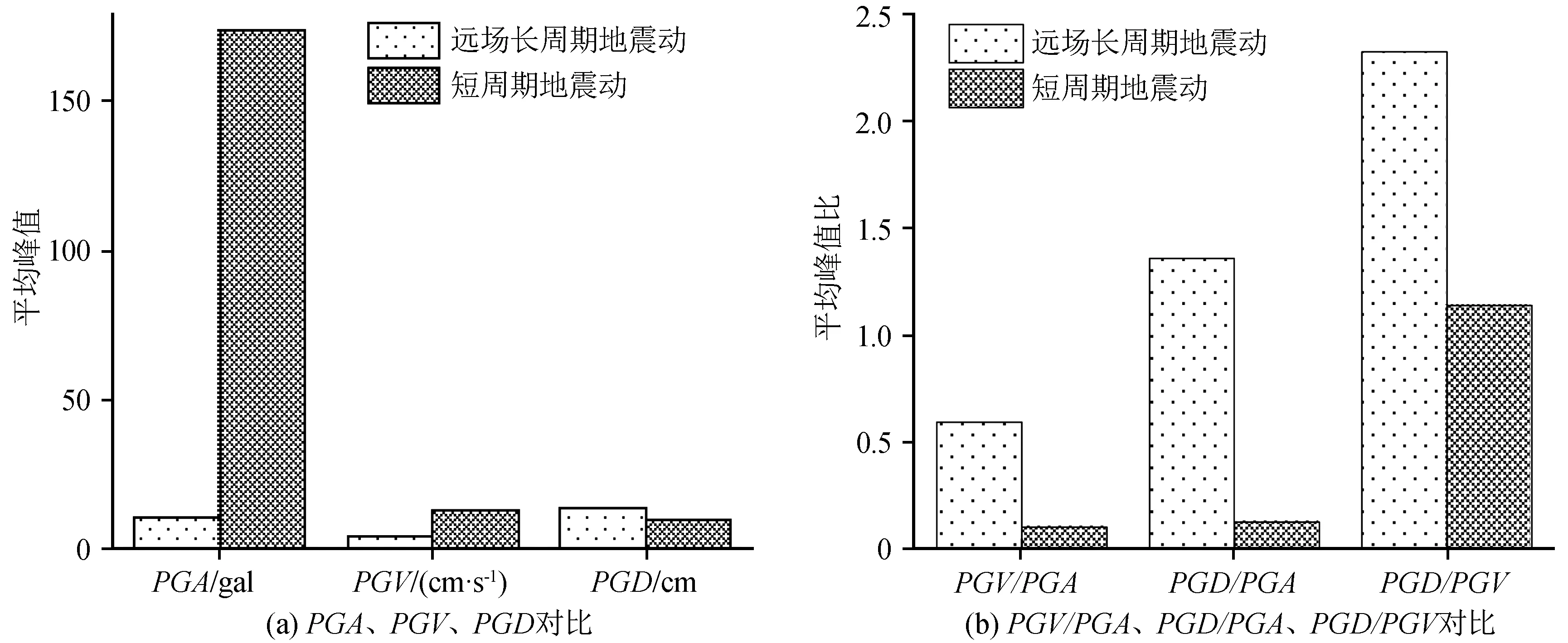
图1 长周期地震动与短周期地震动特性参数对比Fig.1 Comparison between characteristic parameters of long-period and short-period ground motions

2 长、短周期地震波反应谱差异分析

从图1中可以看出,长、短周期地震动平均地面峰值加速度(PGA)的差异最大;短周期地震动的平均地面峰值速度(PGV)是长周期地震动的3.26倍,但平均地面峰值位移(PGD)反而比长周期地震动低10.89%,可见场地土层滤波效应对地震动长周期部分的放大作用。在平均峰值比中,长周期地震动PGV/PGA、PGD/PGA、PGD/PGV值分别为短周期地震动的5.71倍、11.15倍、2.17倍。

采用SeismoSigal软件,取阻尼比为5%,求解出两类不同地震动的加速度、速度以及位移反应谱,对比分析长周期地震动中长周期成分、类谐和波段产生的反应谱差异,如图2～5所示。

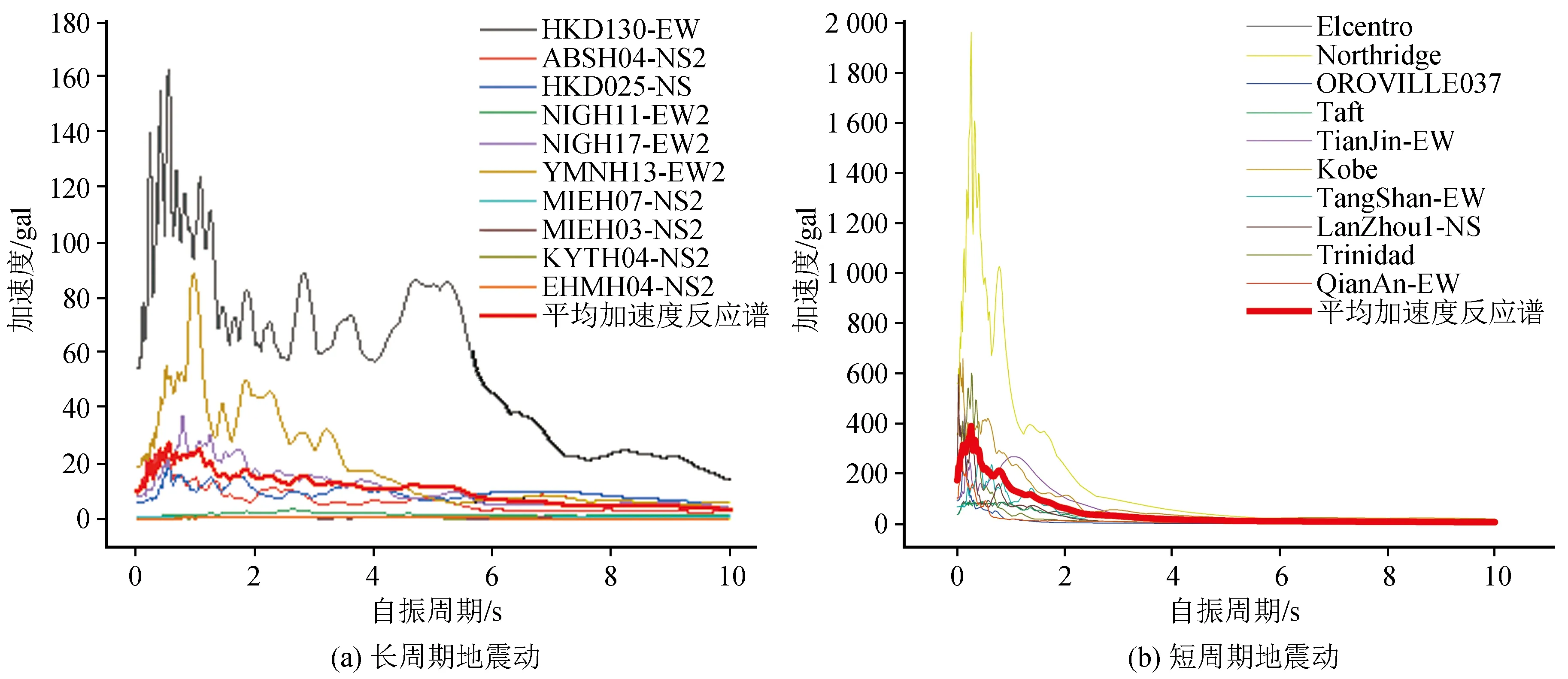
图2 两种地震动的加速度反应谱Fig.2 Acceleration response spectra of two kinds of ground motions

从图2中可以看出,短周期地震动的加速度反应谱随自振周期的增大而快速减小,仅有一个峰值点;长周期地震动加速度反应谱随自振周期的变化过程更为复杂:随着自振周期增大,加速度反应谱增长后缓慢减小,进入平台段,然后继续减小,存在两个甚至多个峰值点,尤其在结构自振周期大于3 s后,加速度反应谱值相较于其最大值仍处于较大水平,而此时短周期地震动则处于较小水平。根据图3可以得出,在整个变化过程中,长周期地震动速度反应谱在自振周期5.6 s前呈线性增长,最终呈现出较大的平台段;短周期地震动速度反应谱在自振周期2 s左右达到最大值,之后处于下降状态,最终呈现出较小的平台段。由图4可知,长周期地震动位移反应谱在自振周期4 s前增长缓慢,自振周期达到4 s后增长较快,整体处于增长态势;短周期地震动位移反应谱在自振周期2 s前增长较快,在2 s左右出现最大值,后期则出现了下降。

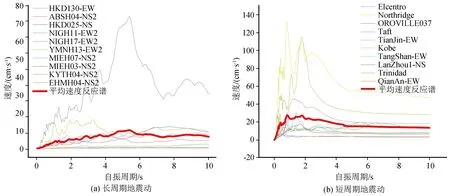
图3 两种地震动的速度反应谱Fig.3 Velocity response spectra of two kinds of ground motions

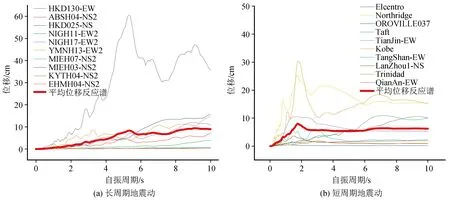
图4 两种地震动的位移反应谱Fig.4 Displacement response spectra of two kinds of ground motions

由两种地震动的平均反应谱(图5)可知,长周期地震动平均加速度反应谱值达到峰值后,下降速度小于短周期地震动,同时长周期地震动加速度反应谱峰值所对应的自振周期大于短周期地震动。对于平均速度反应谱,短周期地震动和长周期地震动分别在自振周期0.83 s、5.36 s处达到峰值。对于平均位移反应谱,由于短周期地震动的能量比较集中,故位移反应谱值增长较快;由于长周期地震动特有的类谐和波段,在自振周期达到4.41 s后其谱值大于短周期地震动,同时二者位移反应谱的差值随着自振周期的增加而增大。

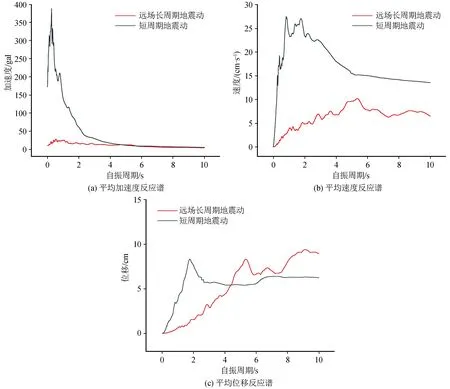
图5 两种地震动平均反应谱Fig.5 Average response spectra of two kinds of ground motions

3 长、短周期地震动作用下高层钢结构响应

利用SAP2000软件建立一个20层钢框架结构模型,输入表1、2中的长、短周期地震动,进行非线性时程分析,对比分析钢框架结构在两类不同地震动作用下的响应差异,研究长周期地震动对结构的破坏特征。

3.1 钢框架结构基准模型的建立

选用美国土木工程师协会(American Society of Civil Engineers,ASCE)推荐的20层钢框架结构基准模型,取其中一榀作为计算模型,总高80.73 m,地面首层受水平约束[8]。钢框架结构质量简化为自重与恒荷载之和,梁荷载取35 kN/m,边柱、中柱荷载分别取125 kN、200 kN,阻尼模型取阻尼比ζ=0.02的Rayleigh阻尼。在梁、柱端的0.1、0.9倍长度处,分别设置FEMA(Federal Emergency Management Agency)356定义的考虑弯矩的M3铰、考虑弯矩和轴力相互作用的P-M2-M3耦合塑性铰[9-11]。

文献[8]中给出了20层Benchmark模型的自振周期,将本文所建立模型前5阶振型的自振周期与文献[8]中的计算结果进行对比,结果列于表3。由表3可知前5阶自振周期的平均误差为1.44%,保证了本文所建立有限元模型的准确性。

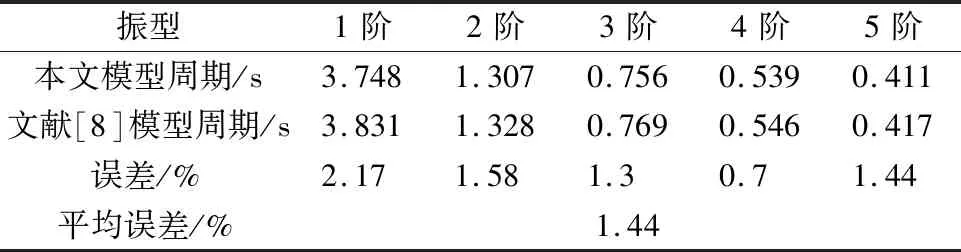
表3 模型自振周期的对比Tabke 3 Comparison between natural vibration periods of two models

3.2 地震动输入与计算

为研究两种地震动对结构动力响应的影响,考虑到调幅对原始地震动的工程特性与结构效应会有所干扰[12],对选定的实际地震动数据不作调整,输入计算模型,时程分析采用非线性直接积分方法,即HHT(Hilber-Hughes-Taylor)法。

式(1)为结构运动微分方程:

(1)

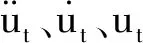
将系数α引入式(1),使用Newmark方法求解,得到HHT法的表达式:

(2)

式中:α取值介于-1/3～0之间。

当α=0时,HHT法还原为常量加速度方法;α取值越小(绝对值越大),高频模态衰减越严重。式(3)为直接积分时程分析中,完整模态阻尼矩阵Cmodal[13-14]的计算方法:

(3)

式中:Ti、ξi和φi分别为模态i的周期、阻尼系数和振型;N为模态总数。

3.3 响应结果分析

经过20次的非线性时程分析,根据钢框架结构的计算结果,得到结构顶点的加速度、速度、位移响应峰值(表4)。根据表4可得,短周期地震动作用下,结构顶点的平均加速度、平均速度响应峰值分别是长周期地震动作用下的5.16倍、1.80倍,差距较大;然而长周期地震动作用下,结构顶点平均位移响应仅比短周期地震动作用下小0.92%,可见位移指标更为敏感。

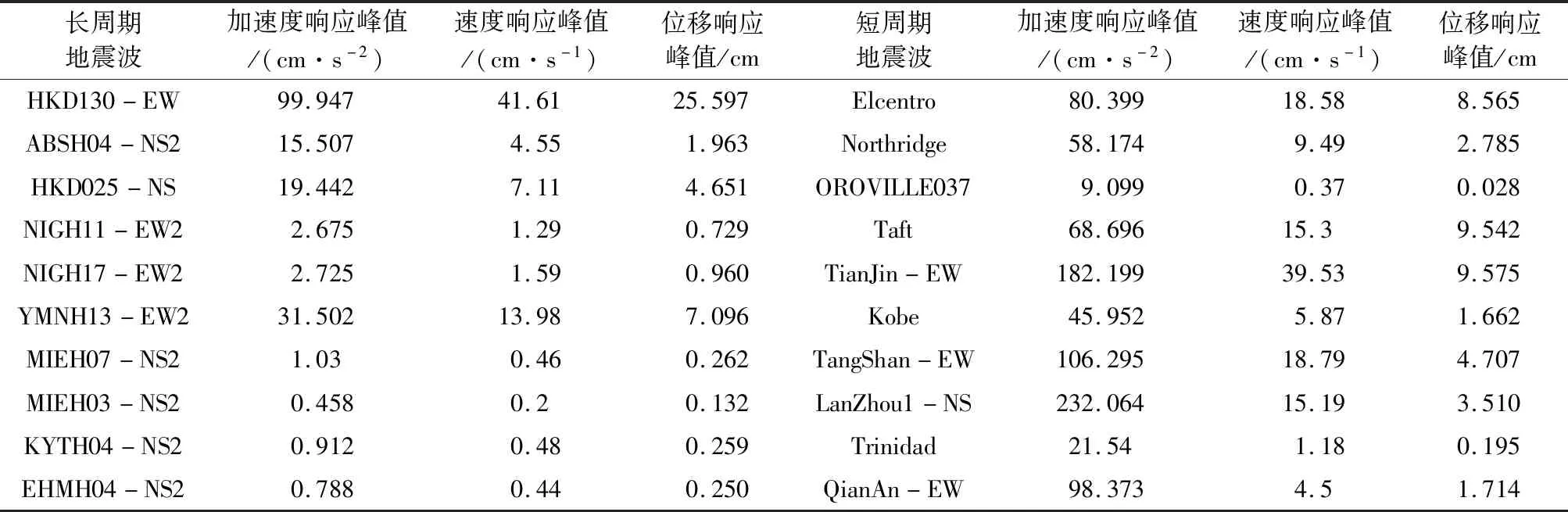
表4 长、短周期地震动作用下结构顶点加速度、速度、位移响应峰值对比Table 4 Comparison between peak values of acceleration,velocity,and displacement response of structure under long- and short-period ground motions

图6、7所示分别为两类地震动作用下楼层位移与总高度之比和层间位移角;图8、9所示为响应平均值。根据表1、2可得,长周期地震动HKD130-EW和短周期地震动TangShan-EW的PGA分别为58.003 gal、65.954 gal,差距较小。而从图6、7可知,HKD130-EW、TangShan-EW作用下的最大层间位移角分别为0.39%、0.134%,长周期地震动作用下响应更大,可见“类共振”效应对结构响应的放大作用很明显。短周期地震动作用下钢框架结构最大层间位移角所在楼层更为分散,竖向突变更显著,容易对结构造成首次超越破坏。长周期地震动作用下钢框架结构的楼层位移与总高度之比更为线性,表现出长时间大幅晃动的运动特征；底部楼层层间位移角响应更强烈且在结构底部影响范围更广,容易对结构底部造成累计损伤破坏，从而导致整体倒塌,对结构抗震极其不利。

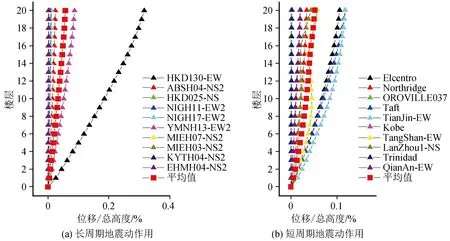
图6 两类地震动作用下结构的楼层位移/总高度Fig.6 Ratio of floor displacement to total height of the structure under two kinds of ground motions

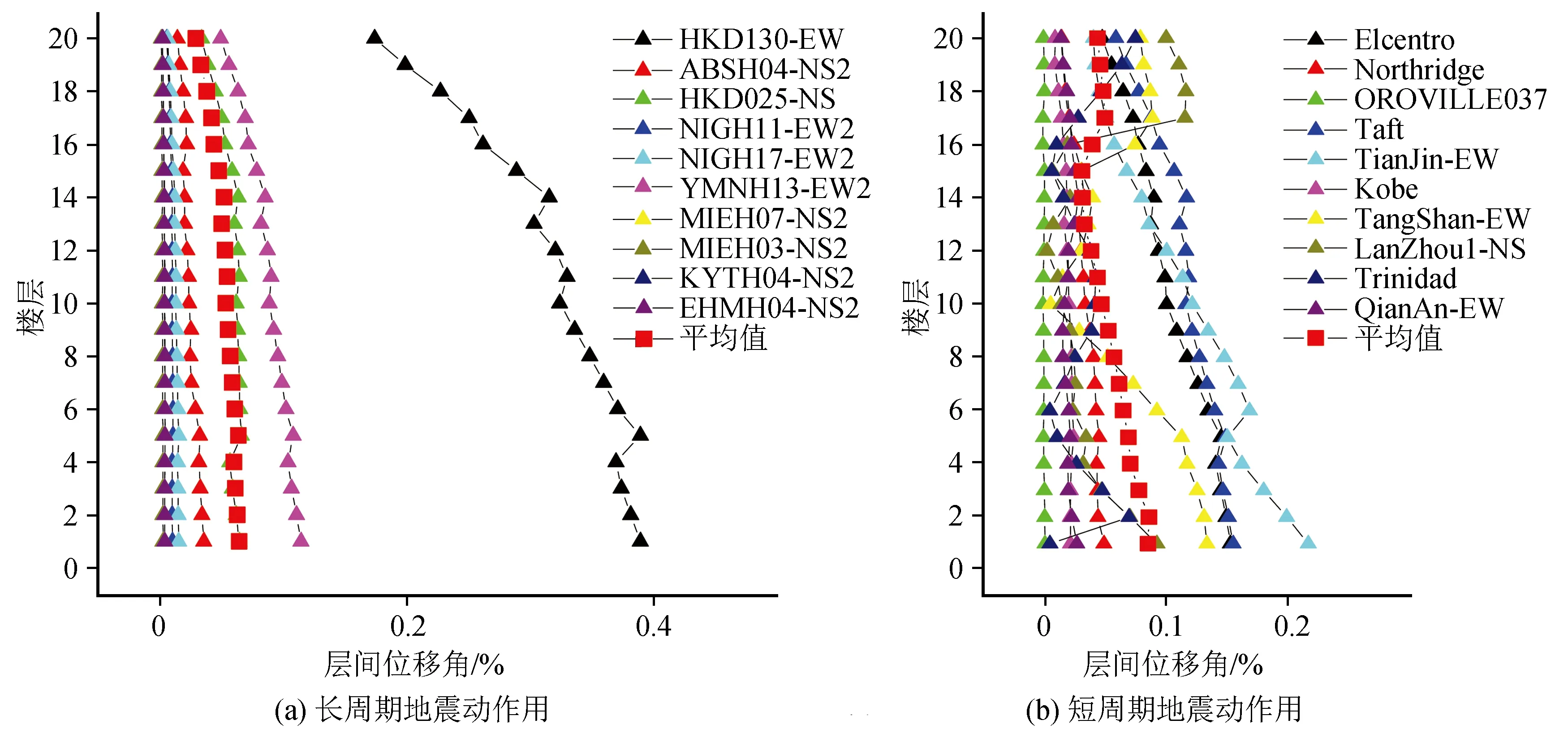
图7 两类地震动作用下结构的层间位移角Fig.7 Story drift ratio of the structure under two kinds of ground motions

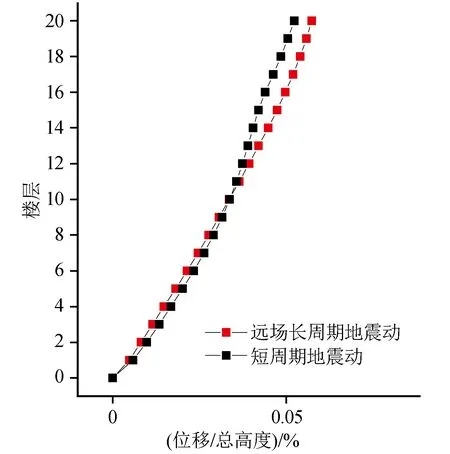
图8 两类地震动作用下平均楼层位移/总高度Fig.8 Average ratio of floor displacement to total height of the structure under two kinds of ground motions

如图8所示,在1～10层,两类地震动作用下平均楼层位移差距较小;高于10层之后,长周期地震动作用产生的位移响应更大,且位移差距随楼层的增高而增大,说明楼层上部受长周期成分影响更为明显。如图9所示,长周期地震动作用下,钢框架结构1～6层的平均层间位移角处于其最大值水平,最大值位于底层;短周期地震动作用下,仅1、2两层的平均层间位移角处于其最大值水平,最大值位于第2层。在9～16层,长周期地震动作用下的平均层间位移角更大;在1～8、17～20层,则相反。

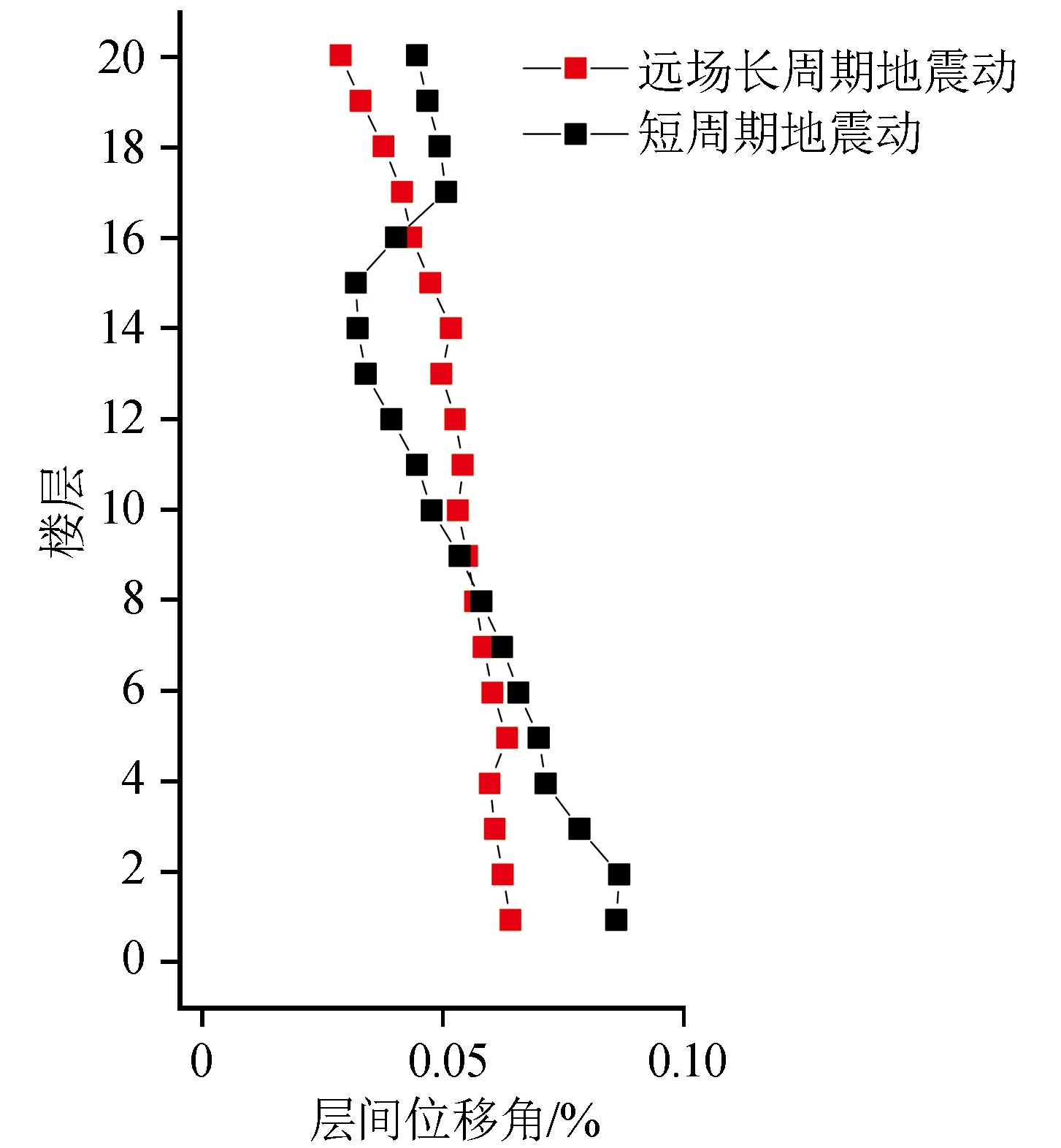
图9 两类地震动作用下平均层间位移角Fig.9 Average story drift ratio of the structure under two kinds of ground motions

4 结论

本文首先比较了长、短期地震动特征参数的差异,然后将不同长、短周期地震动分别输入钢框架结构有限元分析模型,得到钢框架结构在不同地震动作用下响应特征的变化，发现钢框架结构在长周期地震动作用下楼层位移响应更大,结构底部受影响范围更广。对于长周期地震动潜发地区的高层钢框架结构,应针对长、短周期地震动分别考虑震害;对于高层、超高层等中长期结构,建议选择峰值位移作为抗震分析指标。具体结论如下:

(1) 长周期地震动与短周期地震动相比,PGA较小,PGV值小60%以上,PGD值反而大10%以上,软土场地的滤波效应使长周期成分增多且强度被放大。

(2) 基于两种地震动反应谱的对比分析,长周期地震动作用下,对于高层、超高层等中、长周期结构,建议选择峰值位移作为抗震分析指标;对于低层建筑等短周期结构,建议选择峰值加速度作为抗震分析指标。

(3) “类共振”效应使钢框架结构在长周期地震动作用下的结构响应较强,结构长时间发生大幅度振动,结构底部受影响范围更广,容易对结构底部造成累积损伤,导致整体倒塌,对结构的抗震极为不利。

(4) 根据长周期地震动“类共振效应”的震害特征,可通过场地划分、既有建筑结构加固和新建建筑结构针对性设防等方式采取相应的抗震构造措施。