基于模型确认的附着黏滞阻尼器门式刚架地震易损性分析

周 宇,甘露一,赵 青,尚稳齐

(1.安徽建筑大学 建筑健康监测与灾害预防技术国家地方联合工程实验室,安徽 合肥 230601；2.安徽建筑大学 土木工程学院,安徽 合肥 230601;3.安徽省BIM工程中心,安徽 合肥 230601)

0 引言

偶发的地震作用给工程的结构安全带来了巨大威胁,因此对工程结构进行抗震性能分析具有重大意义[1]。地震易损性分析是从统计的角度研究不同地震等级下结构发生破坏的概率[2]。相较于依据设计规范的校核方法评估结构的抗震性能,结合结构性能目标的地震易损性分析方法具有定量评估、结果直观等特点,相关研究已有初步进展且发展态势良好，如郑山锁等[3]研究了钢材锈蚀对钢排架结构地震易损性的影响；张令心等[4]研究了参数不确定性条件下框剪结构的地震易损性。有限元分析结果能否精确地反映工程实际取决于建模参数,且结构模型的真实性将直接影响分析结果的准确性,而上述地震易损性相关研究尚未对有限元建模参数的不确定性展开研究。李天天[5]通过对比有、无隔震设备对结构地震易损性的影响,对结构优化提出建议。文波等[6]考虑相互作用对厂房易损性的影响,为结构加固提供了理论依据。但上述研究在结构优化方面尚未开展直观且精确的优化对比分析。

针对上述模型参数的不确定性和既有分析方法的不足,本文通过一实测结构在环境激励下的时程响应数据,经功率谱分析识别结构模态参数;通过实测尺寸信息及时程响应参数进行有限元建模与确认,建立同尺寸附着黏滞阻尼器的结构模型;基于β分布概率分析二者的地震易损性与抗震性能,进一步提出一种可以直观且精确地反映结构优化程度的曲线:震害优化比曲线(Optimization Ratio Curve of Seismic Damage Index,ORSDI),为工程结构的地震风险评估与结构优化提供新思路。其技术路线见图1,其中x为模型的单元属性值;E为弹性模量;D为模型几何尺寸;K为模型刚度;Jfre为目标函数。

图1 技术路线图Fig.1 Technology roadmap

1 有限元模型确认

常规门式刚架结构有限元模型的建立未考虑实际结构与计算模型在构件尺寸与材料上存在的差异,结构的边界条件也难以实现理想的刚接或铰接,而结构各参数的模糊性对分析结果带来的影响不可忽视[7]。

本文以某典型门式刚架为研究对象,展开有限元模型确认与地震易损性分析研究。该结构横向2跨,跨度均30 m,结构纵向14榀,共180.5 m。梁截面采用H型钢,钢材采用Q355钢,各节点均采用固接。当地抗震设防烈度7度(0.1g),为更好地模拟结构在地震作用下的弹塑性作用,在柱铰处布设P-M-M塑性铰,采用随动硬化滞回模型。

为提高模型的分析精度,对理想的有限元模型进行地震易损性分析时需进一步考虑结构建模参数的不确定性,进行模型确认研究,从而获得更真实、精准的有限元模型。

1.1 试验模态识别

试验模态的识别受测点布设形式的影响较大,原则上测点布设数量越多、覆盖越广,测试精度就越高,但实际工程中因传感器数量不足等问题无法做到理想布设,往往分组分批次进行测试。为使不同批次的测试数据具有可比性,需选择特定响应点作为参考点,参考点的选择需要避开驻点,使其在各阶模态振型下皆有较大的振幅[8]。依据上述测点布设原则,采用DH5907N三向加速度传感器,使用不测力法记录结构在环境激励下的时程响应,并采用功率谱法提取结构的自振频率,识别模态振型(图2)。

图2 结构动力响应图Fig.2 Diagram of structural dynamic response

由图2(a)可知,结构的时程响应峰值为0.05 mm/s。由图2(b)可知,各测点的功率谱中首次出现峰值点的位置基本相同,表明各测点能够识别结构的一阶频率;待一阶频率识别完毕后,令结构一阶频率为0,提取结构的功率谱并识别结构二阶频率,以此识别结构的前二阶模态频率(表1)。由图2(c)可知,结构的一阶振型向着型钢弱轴方向产生平动。

表1 模型修正前后前二阶模态频率Table 1 The first two modal frequencies before and after model correction

1.2 模型确认方法

针对上述算例,以相对误差构建目标函数,分析结构构件参数与目标函数间的敏感性,对目标函数最小值进行求解,开展模型确认研究[9]:

(1) 构建目标函数:定义结构固有频率的计算值与试验值之间的误差为目标函数[10],基于试验模态置信准则理论(Modal Assurance Criterion,MAC)[11]评估试验模态测试的准确性:

(1)

式中:P为修正参数;αfre,i为第i阶固有频率的权重;fa,i为第i阶频率的有限元计算值;fm,i为第i阶频率的试验值。

(2) 修正方法:基于复形法构建一个N维空间,并选取N+1个顶点构成复形多面体[10],在其域内找到一个新点来替换旧的不利点,以构成一个新的多面体。通过上述方法进行多次迭代,使复形多面体不断缩小,逐步逼近最优点。当复形多面体上各顶点的目标函数差值满足计算需要时,目标函数最小顶点称为最优点。理论上迭代的次数越多,最优点越精确,但因运算量大,当目标函数的相对误差在5%内即认为修正完毕。

1.3 有限元模型确认

根据式(1)中复形法的约束条件,对有限元模型进行确认。由表1可知,确认后的模型精度显著提高,试验模态与计算模态在前两阶有较好的重合度(相对误差≤5%),模型结构更加逼近真实结构。由图3可知,迭代次数与相对误差呈显著负相关。由图4可知,模态置信矩阵非对角线元素接近0,对角线元素接近1,结构试验模态的振型符合正交特性,模态测试结果较好。

图3 复形法迭代误差分析Fig.3 Iterative error analysis of the complex method

图4 模态置信矩阵Fig.4 Modal assurance matrix

1.4 附着黏滞阻尼器模型建立

为评估结构模型优化后的抗震性能,基于确认后的模型添加黏滞阻尼器单元,对比二者的减震效果。黏滞阻尼器采用Maxwell单元,刚度为1 kN/mm,阻尼为5 kN,阻尼指数为1。黏滞阻尼器布设在振型幅值较大处有更好的减震效果[12],通过式(2)开展阻尼器布设数量的优化设计:

Pi=μ1Φi,1(Φi,1-Φi-1,1)+μ2Φi,2(Φi,2-Φi-1,2)+μ3Φi,3(Φi,3-Φi-1,3)

(2)

式中:Pi为阻尼器数量;Φi,1,Φi,2,Φi,3为结构前3阶第i跨的振型幅值;μ1,μ2,μ3为前3阶振型权重。

算例仅考虑低阶模态,因此定义前3阶的振型权重分别为:0.7,0.25,0.05,代入式(2)计算结构各榀阻尼器数量。各榀阻尼器数量按计算出的P值四舍五入,取3的倍数成比例对称布设。故算例1～14榀黏滞阻尼器的数量分别为:12、96、18、42、54、39、9、9、15、24、45、48、60、21,结构如图5所示。图5(a)中1-1、2-2、3-3截面的尺寸信息如图5(c)、(d)所示。

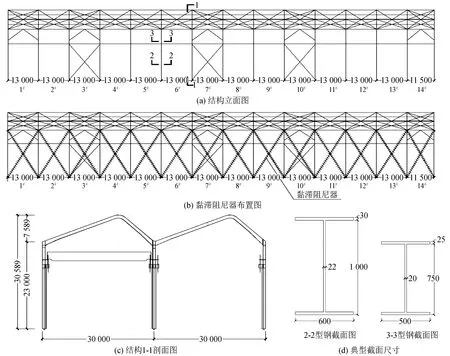
图5 结构几何尺寸信息(单位:mm)Fig.5 Information of structural geometry(Unit:mm)

2 易损性表达方式

2.1 地震动选波与调幅

地震波的不确定性会对结构地震易损性分析产生影响[13],因此本文依据当地抗震设防规范谱,从美国太平洋地震工程研究中心(PEER)强震数据库中选取20条地震动记录,并列于表2。如图6所示,对比规范谱与20条地震动记录的平均反应谱可知,二者的符合度较高,说明所选的地震波符合要求。

图6 平均反应谱与规范反应谱对比Fig.6 Comparison between mean response spectrum and code response spectrum

表2 地震动记录Table 2 Ground motion records

在结构易损性分析中,需对地震动记录进行等步或不等步调幅。本文采用等步调幅原则,即利用固定的等量步长Δλ对地震记录进行调幅[14]:

λi=λi-1+Δλ

(3)

将固定步长设置为0.1g,峰值地面加速度PGA从0.1g等步调幅到1.0g。

2.2 基于β分布的易损性理论

结构的地震需求分析是指结构在地震动作用下维持安全性、适用性所具备的最小能力[15]。通过分析结构超越某一破坏等级的概率大小,评估结构在地震动下的易损性,此时需要定义地震动强度(Intensity Measure,IM)与地震需求参数(Seismic Demand Parameter,SDP)。本文选取结构层间位移角定义地震需求参数,峰值地面加速度PGA定义地震动强度[13]。因地震需求D服从对数正态分布函数[15],故地震动强度和地震需求的中位值mD服从对数线性回归关系:

lnmD/IM=p+qln(IM)

(4)

式中:p、q分别为截距与斜率,可通过回归分析得出。

对数正态分布函数的对数标准差为:

(5)

式中:Sr为残差平方和;N为样本数。

门式刚架结构可通过最大层间位移角定义结构的破坏等级,具体限值如表3所列[6]。结构在不同地震动水平下超越某一破坏等级限值的失效概率为:

(6)

式中:mD/IM为结构地震需求D的中位值;LS为概率抗震能力值,按表3取值;βc为0.399[16];βM与结构破坏限值不确定性有关,取值为0.4[17]。

表3 各性能水平的层间位移角限值Table 3 Story drift ratio limits corresponding to different performance level

根据式(6)所示的结构失效概率,提出基于β分布的地震易损性分析,使易损性矩阵转化为震害指数与峰值地面加速度之间的关系。

定义随机变量x的β概率密度[18]:

BE(x,a,b)=

(7)

式中:a、b为β分布函数的形状参数,a>0,b>0,且满足:

(8)

其中β分布的期望值及方差为:

(9)

(10)

基于上述理论,对既定IM条件下结构各个破坏等级的概率矩阵进行拟合。易损性矩阵中的破坏等级用震害指数Dr表示,该破坏等级的概率密度值为[16]:

(11)

此时地震强度参数i下震害指数的期望值Ei为:

(12)

(13)

联立式(9)、(10)、(12)、(13),得到地震强度i下β分布函数的形状参数ai、bi:

(14)

(15)

由此得到地震强度等级i下的连续型β概率密度函数。

3 地震易损性分析

根据式(3)对所选的地震波进行等步长调幅,开展有限元分析,提取结构最大层间位移角。取地震动强度指标PGA与最大层间位移角的对数,并代入式(4)计算回归关系，将数据结果代入式(6),计算结构超越概率并绘制地震易损性曲线(图7)。依据结构失效概率(表4),提取结构震害矩阵(图8)。根据式(11)计算结构超越某一性能状态下的概率密度(表5),代入式(12)、(13)计算震害指数的方差与期望值,通过式(14)、(15)、(7)得到β分布函数的形状参数与概率密度曲线。将β分布函数的期望值、震害优化比及相应PGA下的β概率密度曲线(表6)绘制于图9中,得到“震害优化比曲线(ORSDI)”，由此可直观、精准地展现结构的震害指数及附着黏滞阻尼器优化后的结构抗震性能。

表5 附着黏滞阻尼器结构的震害指数概率密度Table 5 Seismic damage index probability density of structure with additional viscous damper

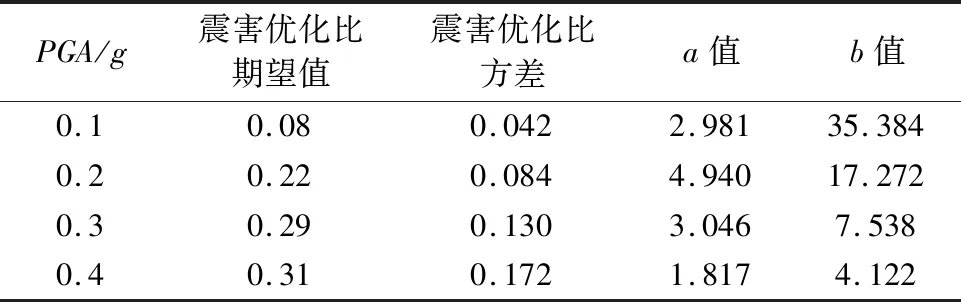
表6 震害优化比的期望值、方差及β函数形状参数值Table 6 The expected value,variance,and β function shape parameter of seismic damage optimization ratio

图7 不同结构的易损性曲线Fig.7 Vulnerability curves of different structures

表4 附着黏滞阻尼器结构的失效概率Table 4 Failure probability of structure with additional viscous damper

图8 结构震害矩阵图Fig.8 Seismic damage matrix of the structure

由图7(a)可知,该门式刚架结构各破坏等级的超越概率随着PGA的增加而增大,当PGA小于0.1g时,轻度损伤曲线的增长速率较快,即结构快速超越完好性能水平,进入轻微破坏阶段；随着PGA进一步增大到1.0g,结构有60%的概率出现结构倒塌。由图7(b)可知,对该门式刚架结构的关键部位附着黏滞阻尼器进行优化后,结构各性能水平下超越概率的增长趋势均有所下降。当PGA逐步增大到0.4g时,结构超越完好性能水平,进入轻微破坏阶段；当PGA增大到1.0g时,相较于初始结构,优化后的结构发生倒塌的概率从60%下降至30%。由图9震害优化比曲线可知,当以期望值作为震害指数评估结构的地震易损性及优化结果时,随着PGA的增大,结构震害指数增长趋势越来越平缓;当PGA逐步增大到0.4g时,结构优化程度达到峰值点,结构优化比为30.6%,减震表现较好。

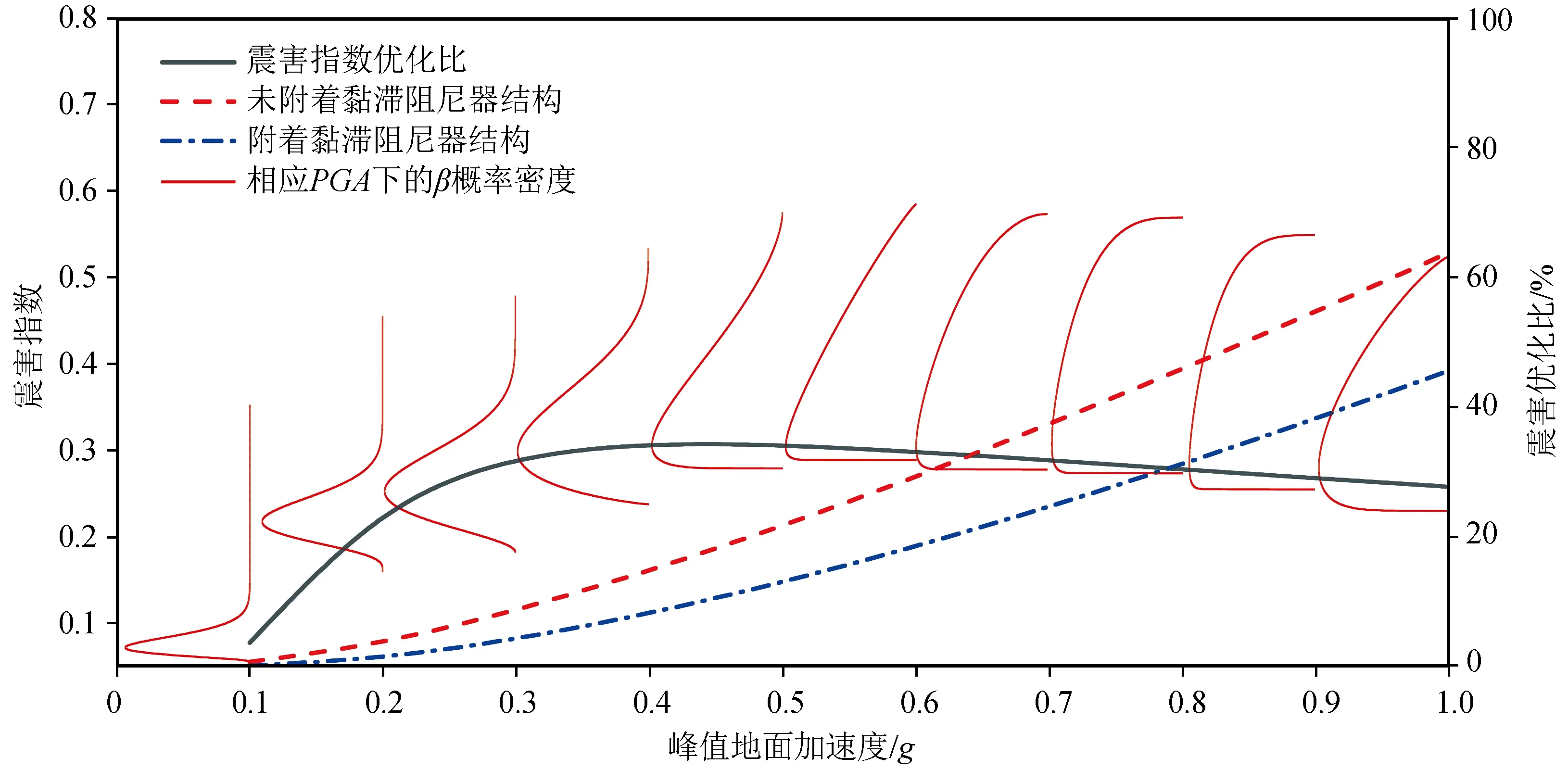
图9 震害优化比曲线Fig.9 The optimization ratio curve of seismic damage index

4 结论

本文依据实测试验数据构建有限元模型,并对有限元结构参数进行模型确认;对确认后的两跨门式刚架有限元模型及附着黏滞阻尼器的优化模型开展地震易损性分析,绘制易损性曲线;依据β分布构建结构的震害矩阵与概率密度,并以期望值作为震害指数建立直观的ORSDI曲线。通过结构的地震易损性分析,可以得到以下结论:

(1) 基于模型确认的方法可最大程度地保证有限元模型接近真实结构。通过模型确认可知,模型结构的相对误差与迭代次数呈显著负相关,且经过十次迭代后,有限元模型的相对误差可减小至5%。

(2) 构建结构地震易损性曲线可定量地评估结构超越各性能水平的概率,得到不同峰值地面加速度下结构的破坏状态,对结构抗震加固具有指导意义。

(3) 基于β分布函数建立的ORSDI曲线可更加直观、准确地展现结构的震害指数及优化程度,并反映出不同PGA下震害指数的分布特性,为结构的震害预测提供科学参考。

(4) 门式刚架结构经附着阻尼器优化后,结构的抗震表现良好,相较于未附着阻尼器的结构,优化后的结构具有更好的减震表现,优化比可达30.6%。

(5) 本文对地震易损性的研究仅考虑主震害作用下结构的易损性,关于余震对结构的持续损害累积尚待深入研究。