基于TSMRFDE和随机森林的旋转机械故障诊断*

宋来建，王晓甜，吴彬彬

(1.西南交通大学机械工程学院，成都 610031；2.重庆科创职业学院人工智能学院，重庆 402160；3.国网河北省电力有限公司营销服务中心，鹿泉 050000)

0 引言

作为工业设备的重要组成，旋转机械的运行状态关乎着生产安全。目前，基于振动信号对旋转机械故障进行检测是最有效和普遍的方法[1-2]。非线性动力学指标，例如各种熵等被广泛用于故障诊断领域，如杨云等[3]将排列熵用于轴承的故障诊断。付文龙等[4]将散布熵(DE)与变分模态分解(VMD)相结合，用于轴承的故障诊断。LI等[5]基于波动散布熵(FDE)和固有时间尺度分解对船舶辐射噪声的特征提取进行了研究，结果表明FDE具有优于DE的特征提取性能。然而，上述熵仅从单一尺度来衡量时间序列的复杂度，分析的不够全面。为此，学者开发了多尺度排列熵(MPE)、多尺度散布熵(MDE)、多尺度波动散布熵等方法。刁宁昆等[6]提出了一种基于MPE和PSO-SVM的滚动轴承故障诊断方法。曲全鹏等[7]提出了基于VMD和MDE的液压泵故障诊断方法，结果表明，MDE相比于单一尺度的DE能够提取更多特征信息，较好地区分液压泵的故障状态。

多尺度波动散布熵(MFDE)具有效率高、抗噪性强等优点[8]。然而，MFDE中的粗粒化处理存在不可避免的缺陷，影响分析的稳定性。粗粒化生成的粗粒序列包含的信息量随着尺度的增加而逐渐减少，造成有效信息的丢失[9]。为此，王勉、张凡等[10-11]在时移粗粒化处理的基础上，结合散布熵，提出了时移多尺度散布熵(TSMDE)，并用于滚动轴承的故障诊断。结果表明TSMDE的有效性和稳定性均优于MDE。

随机森林(RF)作为集成学习的经典方法，具有效率高和性能强的优点，且参数可解释[12]。因此，本文引入RF作为故障分类器，来完成旋转机械的故障识别。综上，针对旋转机械的故障识别问题，提出了一种基于TSMRFDE和RF相结合的故障诊断方法。首先，受到时移粗粒化处理的启发，结合JIAO等[13]提出的反向波动散布熵(RFDE)，提出了TSMRFDE。TSMRFDE优化了MFDE中不全面和不充分的粗粒化处理，使得粗粒化序列包含的信息量随着尺度的增加而增加。此外，TSMRFDE方法通过考虑距离信息具有更强的特征提取性能。随后，将其用于提取旋转机械的故障特征，将得到的TSMRFDE至作为特征信息的表征。其次，针对特征冗余问题，本文引入t-SNE进行降维处理，提高分类效率和精度[14]。最后，将降维后的低维故障特征输入至RF中进行识别，完成了旋转机械故障的精准诊断。

1 时移多尺度反向波动散布熵方法

1.1 反向波动散布熵

JIAO等[13]考虑时间序列中的距离信息，结合波动散布熵，提出了反向波动散布熵。RFDE在效率和性能方面优于传统的熵。给定长度N的序列x={x1,…,xi,…,xN,i=1,…,N}，RFDE的原理描述如下：

(1)基于式(1)所示的正态分布函数：

(1)

式中，μ和σ2分别表示期望和方差。将序列x映射为序列y={yi,j=1,2,…,N},yi∈(0,1)。

(2)通过式(2)所示的线性变换：

(2)

将序列y映射成[1,2,…,c]范围内的数(R为取整运算)，c为类别个数。

(3)

式中，m为嵌入维数；d为延迟系数。所有向量组成的矩阵如下，其中K=N-(m-1)d。

(4)

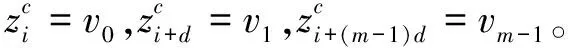
(5)每个散布模式发生的概率计算如下：

(5)

(6)RFDE可以表示如下：

(6)

1.2 时移多尺度反向波动散布熵

TSMRFDE的计算步骤描述如下：

(1)对给定的原始序列{x(i),i=1,…,N}，定义yk,β为：

yk,β=(xk,xk+β,xk+2β,…,xΔ(β,k)β+k)

(7)

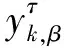
(3)当尺度因子为τ时，对得到的τ个不同的熵值进行平均化处理，即：

(8)

TSMRFDE方法优化了MRFDE方法中不全面的粗粒化处理，降低了对时间序列长度的依赖性，具有更强的特征提取性能。时移粗粒化处理的示意图如图1所示。

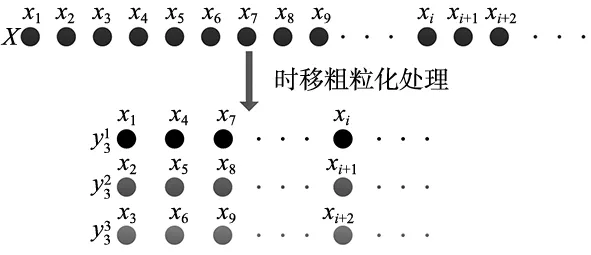
图1 尺度因子为3时的时移粗粒化处理

2 仿真实验分析

为验证TSMRFDE相较于MRFDE的优越性，从两个方面进行验证，分别是对时间序列长度的敏感性和测量时间序列时的稳定性。采用不同长度WGN和1/f噪声开展实验，根据文献[10]设置参数：嵌入维数m=2，类别个数c=5和延迟系数d=1，分别计算WGN和1/f的TSMRFDE和MRFDE值，结果如图2所示。

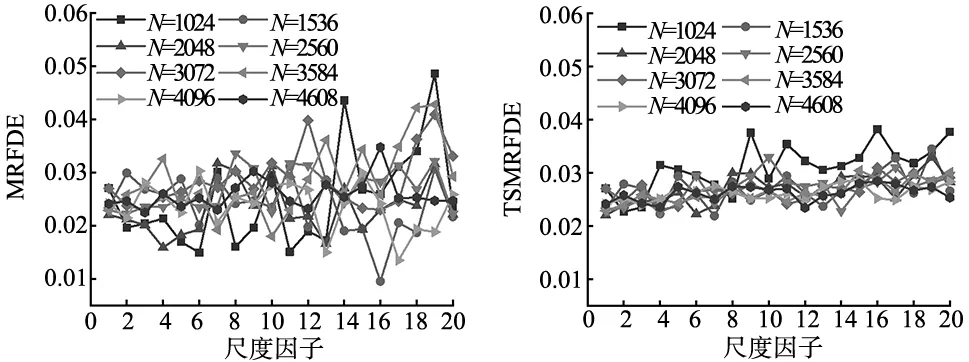
(a) 不同长度下WGN的MRFDE (b) 不同长度下WGN的TSMRFDE

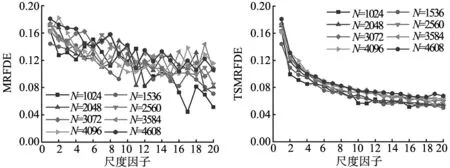
(c) 不同长度下1/f噪声的MRFDE (d) 不同长度下1/f噪声的TSMRFDE

图2a、图2b分别是高斯白噪声的MRFDE和TSMRFDE熵值，图2c、图2d分别是1/f噪声的MRFDE和TSMRFDE熵值。无论是WGN或是1/f噪声，MRFDE和TSMRFDE的趋势大致相同。对比图2a、图2c，MRFDE曲线随着尺度因子的增加发生了波动，特别是在高尺度短序列区域内，波动的更加剧烈。这种现象和之前理论分析中MRFDE对时间序列的尺度及时间序列的长度依赖相对应。对比图2b、 图2d，无论是WGN或1/f噪声TSMRFDE值随着尺度因子的增加不断减少，但其线性随着尺度因子的增加保持相对平滑稳定，即使在高尺度短序列区域中，曲线依然能够保持相对稳定，未出现显著的波动。这可以证明TSMRFDE解决了MRFDE粗粒化不全面的问题。此外，可以发现，当N=2048时，TSMRFDE曲线已经相对平滑，熵值比较稳定。

从信号的波动情况来分析，TSMRFDE提取的特征在稳定性方面显著优于MRFDE。为进一步验证TSMRFDE方法的优越性，利用10组WGN和1/f噪声进行稳定性分析。图3为WGN和1/f噪声的TSMRFDE与MRFDE标准差差值。

从图3a、图3 b可以发现，无论是WGN或是1/f噪声，对应的TSMRFDE标准差减去MRFDE标准差，其差值均小于0，这表明TSMRFDE在分析稳定性方面优于MRFDE。

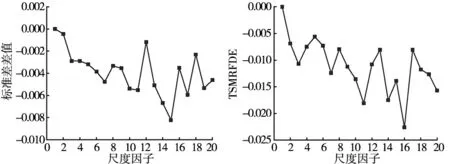
(a) WGN下TSMRFDE与MRFDE的标准差差值 (b) 1/f噪声下TSMRFDE与MRFDE的标准差差值

3 旋转机械智能故障诊断方法

3.1 故障诊断流程

利用TSMRFDE提取旋转机械振动信号的故障特征后，为减少故障特征的冗余，采用t-SNE对原始特征进行降维处理以获得维数低集成度更高的敏感特征。随后，利用RF分类器对旋转机械的不同故障类型和严重程度进行故障识别。基于TSMRFDE，t-SNE和RF的旋转机械故障诊断方法流程如下：

(1)假设旋转机械的工况包含K类，每类工况包含N个样本。对每个样本信号执行M个尺度的TSMRFDE计算，将得到的TSMRFDE值作为故障信号的特征，组成原始特征向量矩阵RN×M。

(2)利用t-SNE算法对初始特征矩阵进行降维处理，获得低维且集成度更高的敏感特征矩阵RN×2。

(3)从每种工况的所有N个样本的敏感特征中选择q个作为分类器的训练样本数据集，剩余N-q个特征作为测试样本数据集。

(4)采用训练样本数据集对基于RF的分类器进行训练，生成训练完备的RF多类别故障分类器。

(5)利用训练完备的RF分类器对测试样本数据集进行智能化的分类，根据输出的类别标签完成旋转机械的故障识别。

3.2 实验验证和分析

3.2.1 实验1

为验证所提故障诊断方法的有效性，利用凯斯西储大学提供的滚动轴承数据集进行实验。测试轴承的型号为6205-2RSJEM SKF深沟球轴承，传感器以12 kHz的频率在1797 rpm的转速下采集驱动端轴承的10种工况振动信号。每种工况振动信号都被分割为互不重叠的58组样本，其中28组样本作为训练数据集，剩余30组样本作为测试数据集。实验数据的详细信息如表1所示。不同工况轴承振动信号的时域波形如图4所示。

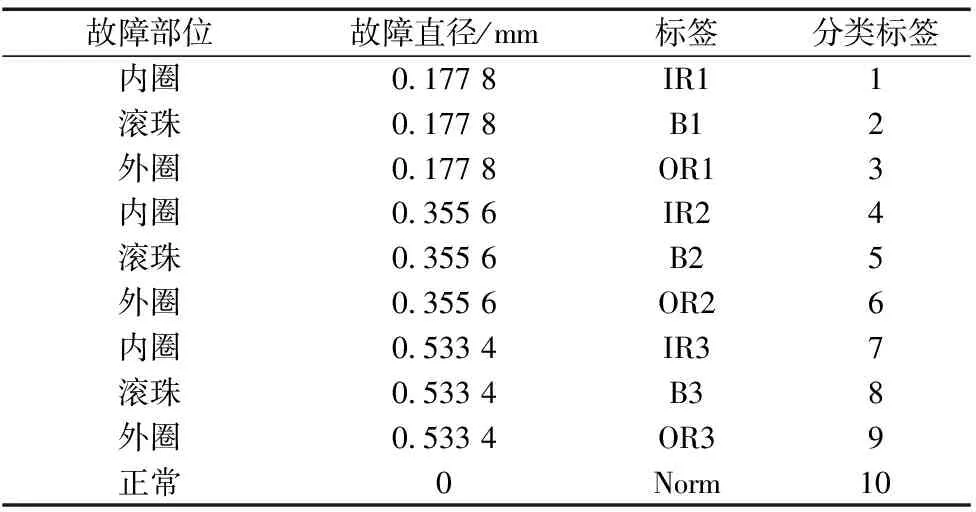
表1 滚动轴承实验数据的详细信息

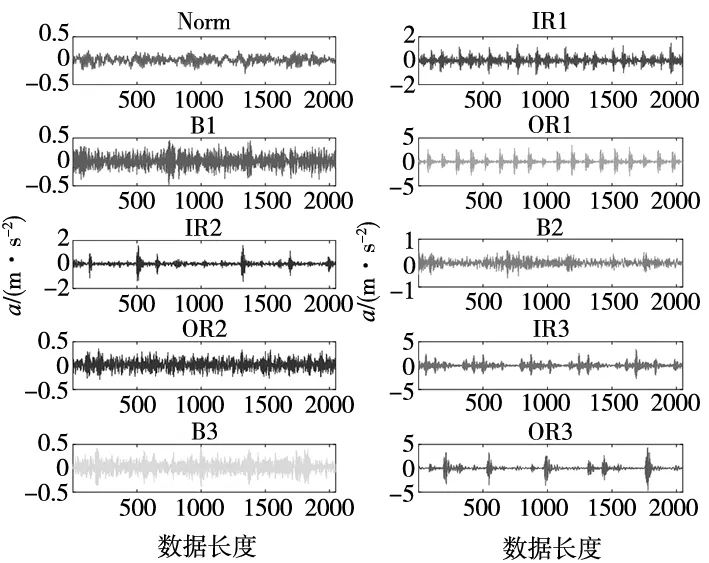
图4 轴承原始信号的时域波形

根据所提方法的流程，采用TSMRFDE和MRFDE方法提取10工况振动信号的故障特征，结果如图5所示。

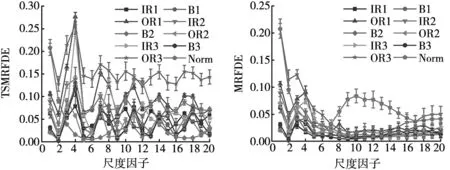
(a) TSMRFDE (b) MRFDE

可以发现，TSMRFDE的标准差明显要小于MRFDE的标准差，特别是Norm样本。这表明TSMRFDE在稳定性方面优于MRFDE。然而，可以发现在部分尺度上，TSMRFDE和MRFDE值存在较为明显的混叠，需要进行降维以增强特征的分辨率。因此，采用t-SNE对原始特征进行降维，结果如图6所示。

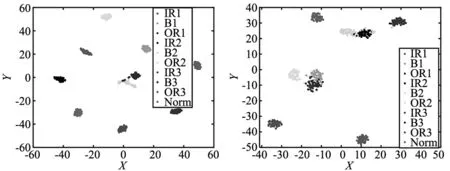
(a) TSMRFDE (b) MRFDE

可以发现，TSMRFDE在降维后，相同工况样本都有明显的聚类中心，不同工况样本都互相分离，这表明特征经过降维具有优异的区分度，也证明了TSMRFDE初始特征具有较高的质量。反之，MRFDE特征在降维后发生了明显的混叠，如B3样本和B1样本，IR2样本和B2样本。此外，同一类别样本的聚集度也小于TSMRFDE，这表明MRFDE特征的质量低于TSMRFDE。

随后，将低维特征输入至RF分类器进行训练和识别。TSMRFDE和MRFDE特征的测试集识别结果如图7所示。可以发现，TSMRFDE方法取得了100%的分类准确率，这表明该方法能够有效的检测滚动轴承的不同故障类型和严重程度。MRFDE方法的识别准确率为95.67%，特别是B2样本的识别准确率仅为70%，有9个样本出现了错误分类，证明了MRFDE方法无法有效的检测B2故障。

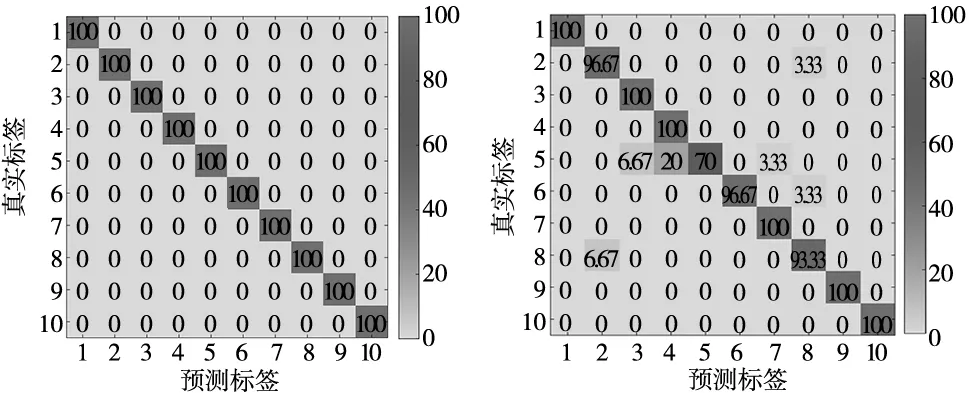
(a) TSMRFDE (b) MRFDE

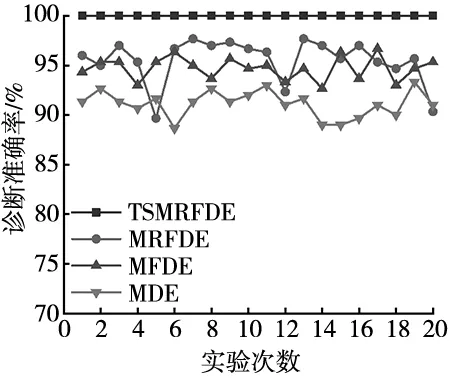
图8 20次实验下4种方法的故障诊断结果

此外，为了全面地验证所提方法的优越性，将TSMRFDE与MRFDE、MFDE和MDE进行对比。每种方法的参数设置都保持相同，4种方法的20次分类结果分别如图8和表2所示。

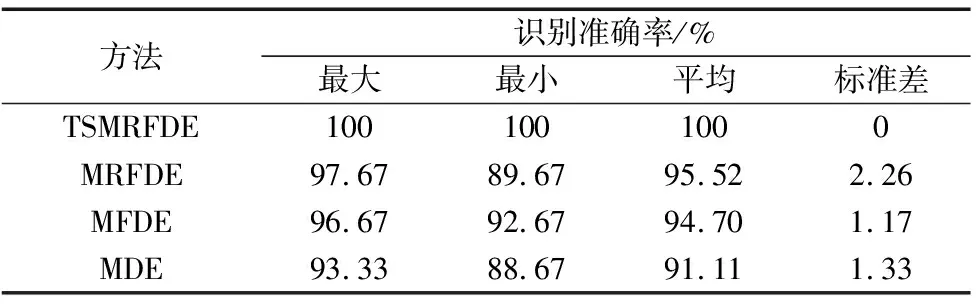
表2 20次实验下4种方法的识别准确率

从表2可以发现，即使开展多次实验，TSMRFDE方法的平均识别准确率也达到了100%，证明其具有优异的稳定性和可靠性。另外3种方法的平均识别准确率分别为95.52%、94.70%、91.11%，均低于TSMRFDE，证明了TSMRFDE的优越性。此外，可以发现虽然MRFDE方法的标准差大于MFDE的标准差，但MRFDE方法的平均识别准确率高于MFDE，这证明了MRFDE方法具有相对优异的性能，但容易出现不稳定的结果，仍然证明了MRFDE优于MFDE。

3.2.2 实验2

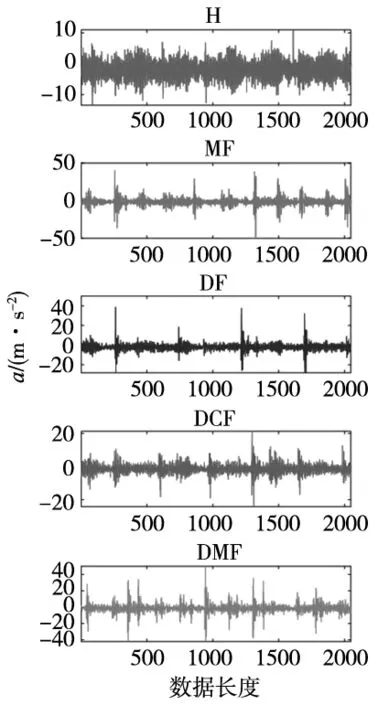
图9 齿轮箱原始信号的时域波形

为了验证所提方法的通用性，利用齿轮箱故障数据集来进行验证。实验数据采集于QPZZ-Ⅱ故障模拟实验平台。实验中电动机的转速设置为880 r/min，未引入负载。齿轮箱包括1个主动的齿数为55的小齿轮和1个从动的齿数为75的大齿轮。人为设置了5种齿轮箱工况，分别是齿轮点蚀故障(DF)、齿轮磨损故障(MF)、齿轮断齿故障(DCF)和点蚀&磨损复合故障(DMF)以及健康状态(H)。利用安装在输入轴的加速度计在5.12 kHz的频率下收集齿轮箱振动信号。每个工况的样本都分割为26组长度为2048的互不重叠样本。其中16组样本用于训练，剩余10组样本用于测试。样本的简要介绍如表3所示。图9为不同工况齿轮箱振动信号的时域波形。

表3 实验2数据的简要介绍

同样的，计算5种工况齿轮箱振动信号的TSMRFDE和MRFDE均值标准差，结果如图10所示。

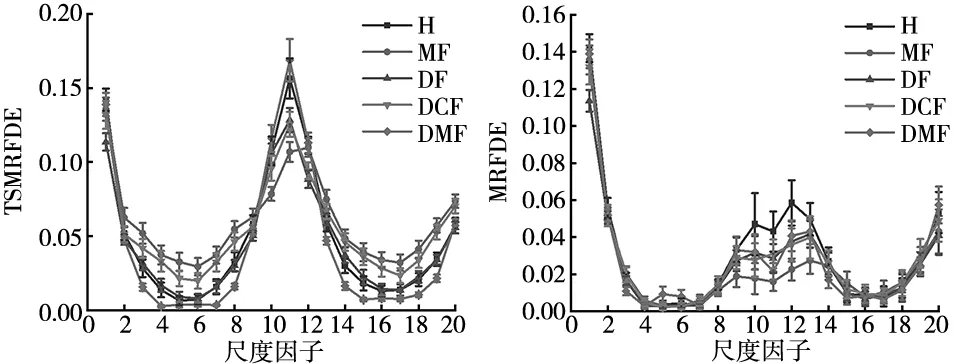
(a) TSMRFDE (b) MRFDE

可以发现，TSMRFDE的标准差要小于MRFDE的标准差，特别是DMF样本，这证明了TSMRFDE方法的稳定性优于MRFDE。此外，在各个尺度上，TSMRFDE曲线的分辨率也要优于MRFDE曲线。在尺度为10～13时，MRFDE曲线具有一定的区分度，而TSMRFDE曲线在各尺度上的区分度更加显著。因此，从特征的提取性能来对比，可以证明TSMRFDE优于MRFDE。

随后，利用t-SNE对原始故障特征进行降维，以进一步增强特征的分辨率。TSMRFDE和MRFDE特征经t-SNE降维后的可视化结果如图11所示。

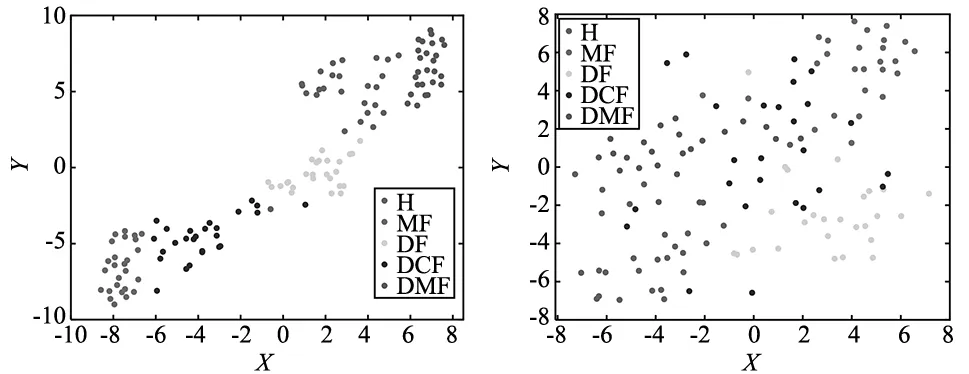
(a) TSMRFD (b) MRFDE

可以发现，TSMRFDE的可视化结果较优异，各工况样本都存在相对显著的聚类中心，同一类别的样本都互相聚集，不同样本之间互相分离。虽然样本H和样本DCF出现了部分的混叠，但总体上具有非常明显的区分度。而MRFDE的可视化结果较差，各工况样本分布的非常分散，无法找到聚类中心，并且不同样本互相混叠，各类别样本的聚集度也低于TSMRFDE。因此，这证明TSMRFDE方法提取的故障特征具有较高的质量，优于MRFDE。

随后，将低维的故障特征输入至RF分类器进行训练和识别。TSMRFDE和MRFDE特征的测试集识别结果如图12所示。

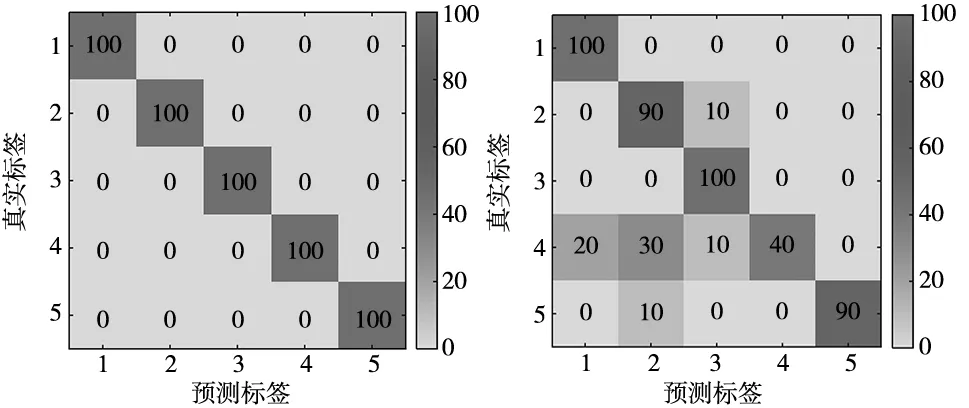
(a) TSMRFDE (b) MRFDE

可以发现，TSMRFDE方法的分类准确率为100%，即所有样本都得到了准确分类，验证了其在齿轮箱故障识别中的有效性。MRFDE方法的识别准确率为84%，特别是DCF样本的识别准确率仅为40%，有6个样本出现了错误分类，这证明了MRFDE方法无法有效的检测DCF故障。

同样的，为了全面和准确评估TSMRFDE方法的有效性和优越性，利用MRFDE，MFDE和MDE在20次分类下的故障识别结果进行对比。4种方法的20次实验结果如图13和表4所示。可以发现，TSMRFDE方法的平均准确率为97.9%，高于另外3种方法，验证了其有效性和优越性。此外，TSMRFDE方法的标准差也小于其它方法，证明了其稳定性。

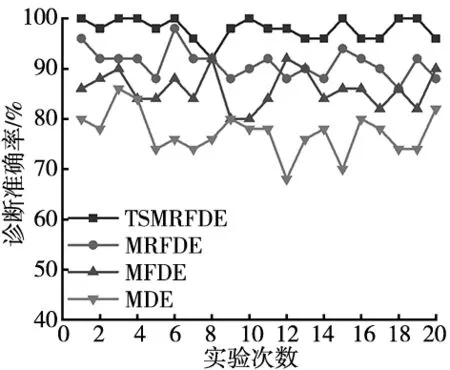
图13 20次实验下4种方法的故障诊断结果

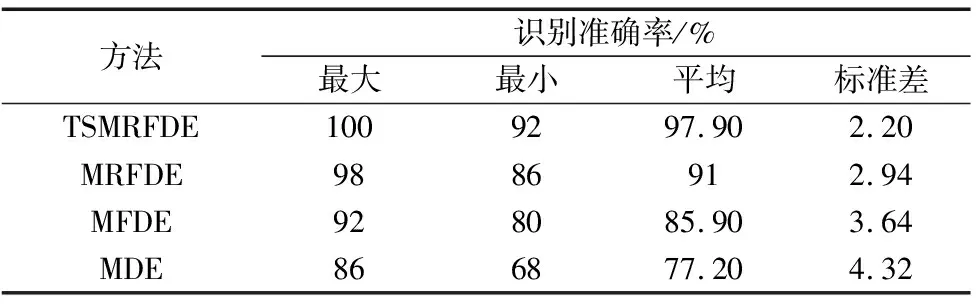
表4 20次实验下4种方法的识别准确率

4 结论

(1)本文在FDE的基础上，引入时移粗粒化处理来实现信号的多尺度分析，并考虑了距离信息，提出了TSMRFDE。通过理论介绍和仿真信号分析，证明了TSMRFDE对时间序列长度的依赖性小于MRFDE，并且具有更高的稳定性。

(2)开发了一种基于TSMRFDE，t-SNE和RF的旋转机械故障诊断方法，利用滚动轴承和齿轮箱两组数据集验证了所提方法的有效性和泛化性，能够准确的识别旋转机械的故障类型和故障程度，相比于另外3种方法具有更加显著的优势。

然而，所提方法也存在一些不足，如TSMRFDE需要人为的设置参数，没有严格的设置标准。未来将对参数的自适应设置进行研究，例如优化算法进行优化等。