基于分数阶滑模永磁同步电机调速*

邓 豪，曹 勇，何志琴

(贵州大学电气工程学院，贵阳 550025)

0 引言

永磁同步电机因具有高功率密度、体积小、调速范围广、具有高可靠性等特点，在工业控制、航空航天、电动汽车、医疗器械都具有广泛的应用[1]。由于永磁同步电机是多变量、强耦合、非线性控制对象[2]，传统的PI控制只能满足简单工况的环境，当受到参数变化以及外界扰动的情况下，系统的鲁棒性将受到较大影响。

滑模控制作为一种非线性变结构控制，当系统参数以及负载发生变化时，具有很好的抗扰能力和鲁棒性。但是滑模控制在滑动模态时，会在滑模面进行来回穿越产生抖振。因此许多学者采用了不同办法来消除控制过程中会带来的抖振。郭征华等[3]在传统指数趋近律中引入系统的状态变量来设计新型趋近律，加快了趋近过程，同时当系统状态处于滑动模态时，系统在滑模面上的切换过程不再是带状，而是逐步减小的过程。KANG等[4]通过对双幂次趋近律进行收敛时间以及相轨迹分析，提出一种通过构造反正切辅助函数双幂次趋近律，将该趋近律应用于二阶系统，从收敛时间，系统抖振，抗干扰性分析了其优越性。

随着分数阶理论的不断发展和完善，近年来分数阶控制被广泛应用于线性和非线性系统，例如分数阶PI控制[5]，分数阶自抗扰控制[6]，分数阶滑模控制[7]。分数阶微积分相比整数阶多了俩个可调参数，自由度更大，调节参数更加灵活。由于分数阶微积分的优越性，许多学者结合分数阶微积分和滑模控制将其引入永磁同步电机控制中。GAO等[8]提出一种分数阶PID滑模面，并利用所提滑模面提出一种指数趋近律应用于永磁同步电机调速系统中，提高了系统的响应速度，抑制了系统抖振。王兴亮等[9]提出一种分数阶快速终端滑模速度环控制，有效降低了系统抖振，为了进一步提高系统的抗干扰能力，设计了分数阶观测器进行前馈补偿，提高了系统的鲁棒性。

为了减小滑模控制的固有抖振问题，将整数阶滑模面扩展到分数阶滑模面，利用分数阶微积分随时间缓慢衰减特性，设计分数阶滑模面。同时提出一种新型趋近律，使的系统状态可以根据距离滑模面的远近参数自适应调整，有效减小了系统的抖振。同时为了避免参数的反复试凑，引入粒子群算法进行参数寻优。最后通过仿真验证所提分数阶滑模控制的优越性。

1 趋近律设计与分析

1.1 传统趋近律

为了改善滑模控制的品质，提出了趋近律概念，并设计指数趋近律如下所示：

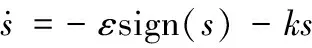
(1)

式中，ε、k为大于0的常数；s为滑模面；sign()为符号函数；ks为指数项；-εsign(s)为等速趋近项。

当系统的初始状态S(0)远离滑模面的时候，此时通过调整指数项和等速项参数同时来完成趋近模态。当系统状态点到达滑模面时，此时指数项为0，由等速项来完成滑动模态。由于等速项含有符号函数，ε不可能为0，所以系统将一直伴随着以ε大小的抖振。

1.2 新型趋近律

为了克服传统指数趋近律的缺点，本文所提趋近律可表达为：

(2)

式中，k1、k2为大于0的常数；0<γ<1；0<σ<0.1。

与传统的指数趋近律相比，本文所提的趋近律参数k1是自适应变化的，而不是像指数趋近律中的等速项ε是一个固定的常数。对所提趋近律进行趋近模态和滑动模态进行分析如下：

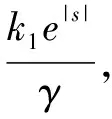
滑动模态：当系统状态接近滑模面时，即s→0时，此时指数项k2s为0，由等速项起作用，此时e-|s|→1,σ|s|→1，等速项为k1/(γ+1)，系统将以一个很小的数在滑模面上滑动，有效减小了抖振。

为了进一步消除系统由于sign函数所带来的抖振，文中选取双曲正弦函数作为系统滑动模态的切换函数，使得其切换过程更加平滑。

最终，所提出的新型趋近律如下：

(3)

为了分析本文所提趋近律的稳定性，通过构造如下的Lyapunov函数：

(4)

对式(4)进行求导，即可得到如下：

(5)

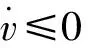
2 分数阶微积分

(6)

式中，a和t表示算子的上下限；α表示为微积分的阶次。

分数阶微积分在几百年的发展过程中，出现了多种定义，其中Grunwald-Letnikov、Riemann-Liouville、Caputo定义最为常见：

本文以Caputo定义进行介绍，Caputo分数阶微积分定义表达式为：

(7)

式中，Γ()为gamma函数，定义如下：

(8)

分数阶微积分具有如下性质：

线性性质：

(9)

叠加性质：

(10)

3 永磁同步电机数学模型

为了简化分析，建立一个理想的永磁同步电机数学模型，对PMSM提出如下假设：忽略永磁同步电机铁芯饱和，忽略磁滞和涡流的影响，磁通势成正弦分布，忽略由于定子槽不规则所产生的影响[10]。

永磁同步电机在d-q轴下的数学模型如下所示：

(11)

磁链方程为：

(12)

式中，ud、uq是d-q轴下的定子电压；id、iq是d-q轴下的定子电流；Ld、Lq是d-q轴下的定子电感；R是定子电阻；ψd、ψq是d-q轴下的磁链；ψf是永磁体磁链；ωe是机械角速度；ω是电气角速度；Pn是电机极对数。

电磁转矩方程如下所示：

(13)

本文以表贴式永磁同步电机为例，因此Ld=Lq=L，所以新电磁转矩方程为：

(14)

运动方程为：

(15)

3.1 PMSM速度环滑模设计

定义永磁同步电机系统状态变量如下所示：

(16)

式中，x1、x2为系统的状态变量；ωe为给定速度；ω为参考速度。

结合式(15)和式(16)可以得到：

(17)

(18)

为了消除系统稳态误差，选取积分滑模面作为系统的切换函数，表达式如下：

(19)

对式(19)进行求导，并结合所提出的新型趋近律，可设计永磁同步电机滑模速度环的控制表达式如下：

(20)

3.2 分数阶滑模速度环设计

为了对比分数阶滑模控制的优越性，选取如下的分数阶滑模面：

S=x1+βD-λ-1x1

(21)

式中，β为积分增益；λ为分数阶的阶数。

对式(21)求导可得：

(22)

结合式(17)、式(22)，可以得到控制器的输出为：

(23)

4 粒子群算法

粒子群算法是一种智能优化算法[11]，其核心思想是通过模仿鸟类的觅食行为，将空间的每一只鸟抽象为一个粒子，每一个粒子代表求解问题的可行解。多个粒子组成为一个种群，每一个粒子都有各自的位置，速度和适应度函数值信息。在每一次迭代的过程中，每个粒子根据自身的位置，个体极值和全局极值来调整速度和方向。其速度和位置更新公式如下：

(24)

式中，ω为惯性权重；c1、c2为学习因子，通常设为1.5；r1、r2为(0～1)之间的随机数。

在粒子群算法中惯性权重ω对算法的寻优能力有较大的影响，在算法优化早期较大的惯性权重可以增强全局探索能力，有利于得到寻优最佳值。在算法优化后期较小的惯性权重可以增强算法局部探索能力。常规的粒子群算法惯性权重是一个固定常数，算法寻优能力差。采用一种线性递减权重更新方式，表达式如下：

(25)

式中，ωmax、ωmin为ω的最大值和最小值；t为当前迭代值；tmax为总的迭代值，一般ωmax=0.9，ωmin=0.4。

(1)首先对粒子进行赋值，在文中目标函数的空间为6维，初始化种群为30，第i个粒子在空间的位置表示为：Xi=[xi1,xi2,xi3,xi4,xi5,xi6]，速度表示为Vi=[vi1,vi2,vi3,vi4,vi5,vi6]，其中第i个粒子的个体最优位置为pid=[pi1,pi2,pi3,pi4,pi5,pi6]，全局最优位置为：pgd=[pg1,pg2,pg3,pg4,pg5,pg6]。

(2)选择适应度函数如下所示：

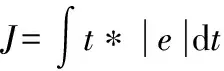
(26)

(3)设置最大迭代次数为30，通过不断迭代找到最小适应度函数的粒子，该粒子在搜索空间的位置是最佳滑模参数。

(4)判断算法是否满足约束条件，如果满足则结束寻优，输出最佳参数。如不满足结束条件，则继续寻优。

5 仿真实验结果

图1为基于所提新型趋近律永磁同步电机滑模速度环结构框图，采用id=0控制策略，利用参考转速和实际转速之间的误差，设计了分数阶滑模控制器对转速进行控制，并引入粒子群算法对滑模参数进行整定，进而提高PMSM控制性能。

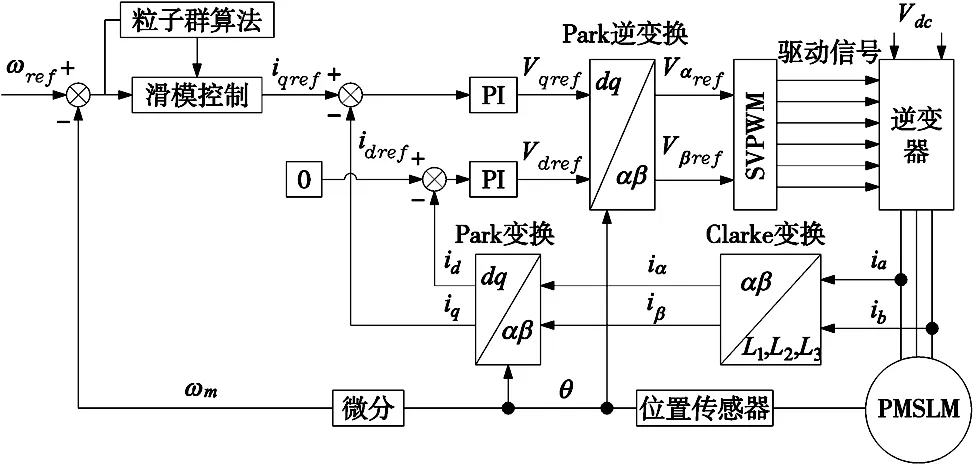
图1 永磁同步电机矢量控制结构框图

本文在MATLAB/Simulink仿真所采用的PMSM模型参数如下所示：定子电阻为R=2.875 Ω，电感Ld=Lq=0.008 5 mH，磁通φ=0.175 Wb，转矩系数为1.05 N·m/A，转动惯量J=0.003 kg·m2，极对数为4。为了验证本文所提出趋近律的优越性，将提出的趋近律和指数趋近律相比较。

为了保证仿真对比的准确性，电流环参数保持一致，速度环分别采用新型趋近律和指数趋近律进行控制。指数趋近律参数选取分别为ε=200，k=300，c=60。新型趋近律通过采用粒子群进行在线优化，其优化参数分别为：k1=1.12，k2=125.25，γ=0.45，σ=0.01，c=2.51。分数阶滑模控制参数为：k1=0.12，k2=260.4，γ=0.55，σ=0.013，β=2，λ=0.089。

为了验证永磁同步电机采用新型滑模转速环控制动态性能，系统仿真时在初始时刻设置空载转速为1000 r/min,为了对比系统的抗干扰性，在0.2 s时给系统突加5 N的负载，其转速对比、电磁转矩对比如图2和图3所示。

图2 转速对比 图3 电磁转矩对比

从图2转速对比曲线来看，采用指数趋近律设计的滑模速度环，系统有较快的响应，但是在初始时刻超调量大(31%)，跟踪时间长(0.06 s)，采用新型趋近律滑模速度环，响应速度较快快(0.05 s)，并且转速无超调，在分数阶滑模控制方式下，响应速度快(0.02 s)，转速无超调。当系统在0.2 s突加负载时，指数趋近律转速波动大(50 r/min)，恢复时间长，新型趋近律转速波动较小(10 r/min)，具有较快地恢复时间，采用用分数阶滑模控制，转速波动小(5 r/min)，抗负载能力强。

图3电磁转矩对比结果表明，指数趋近律控制下的转矩在初始时刻波动大，在0.2 s突加负载时，电磁转矩达到稳定时间长，在新型趋近律控制方式下，初始时间电磁转矩波动较小，同时在0.2 s 突加负载时，电磁转矩能够在很短的时间里跟踪并达到稳定，在分数阶滑模控制方式下，初始时间电磁转矩波动更加且平稳，在0.2 s突加负载时，电磁转矩能够快速跟踪并稳定。从上面的结果对比分析图可以得出，永磁同步电机采用所提的趋近律设计的分数阶滑模速度环比指数趋近律，新型趋近律控制方式动态特性好，鲁棒性强。

为了验证分数阶滑模速度环控制受参数变化以及负载扰动时系统的鲁棒性，首先设置转速为1000 r/min，在0.2 s负载突变到5 N，在0.3 s时转速增加1200 r/min。对于参数变化，本文选择转动惯量作为验证，分别选择J=0.5J和J=2J进行比较。

从图4可以看出当转动惯量发生变化时，转速能够迅速响应并达到稳态，转矩和电流在0.2 s负载突变时波动小，在转速上升到1200 r/min时，转矩有一定的波动，但能够在短时间到达稳态。

图4 转动惯量变化时速度、转矩对比图

6 结论

为了解决永磁同步电机采用传统滑模控制应用于速度环控制动态特性不好、鲁棒性差等问题。提出一种分数阶滑模速度环控制，利用分数阶微积分随时间缓慢衰减特性，有效减小系统抖振。同时提出一种新型趋近律，该趋近律在传统的指数趋近律上进行改进，对等速项引入自适应因子γe-|s|+σ|s|解决滑模控制在快速性和抖振之间的矛盾，引入双曲正切函数进一步减小由符号函数切换过程带来的抖振。通过采用分数阶滑模面和新型趋近律来设计控制器，仿真结果表明，采用分数阶滑模面和新型趋近律设计的滑模速度环，能够加快系统的响应速度且转速无超调，减小系统的稳态误差，同时电磁转矩波动更小；当电机参数和负载发生变化时，转速和电磁转矩能够快速响应达到稳态，提高了系统的鲁棒性，验证了所提方法的有效性。