基于贝叶斯更新和荷载信息的桥梁时变可靠度评估
韩育刚
(广西上横高速公路有限公司,广西 南宁 530000)
由于恶劣的环境和不断增加的交通量和负载,在役桥梁可能会随着时间的推移而退化,从而降低桥梁的可用性。由于服役可靠性最终可能会低于为新桥指定的可接受水平,因此必须经常就这些桥的“安全性”做出决定。在荷载预测和桥梁承载能力估算中都存在不确定性的情况下,可靠性分析为不确定性下的决策提供了一个合理的准则,是一种有效的决策工具[1,2]。
由于抗力和荷载等参数在结构服役期间不是恒定不变的,因此计算出的可靠度也具有时变的特点。此外,通过历史荷载试验信息可获得截断荷载从而截断桥梁抗力的上尾分布,引起抗力的统计参数改变。历史荷载对于可靠度评估具有重要的修正补充作用。李全旺等[3]基于采用历史荷载信息作为截断荷载,建立了多种劣化因素下的桥梁抗力更新方法。另外,部分学者也开展了利用荷载试验进行贝叶斯更新方面的研究,贝叶斯方法通过确定先验分布,并以检测或监测数据建立似然函数,进而得到变量的后验分布,不仅可以有效利用多源数据,还能减少先验模型的不确定性,提高预测精度,在机械、航天、土木等领域得到了广泛应用,然而对于历史荷载信息的贝叶斯更新鲜有报道,如何有效利用历史荷载信息开展可靠度评估亟需进一步研究。
1 桥梁时变可靠度计算
桥梁在服役期间会受到多方面因素的随机影响,如恒荷载、冲击荷载、风荷载等,在进行桥梁可靠度计算时应将这些因素作为随机变量X1,X2,…,Xn来考虑,形成的结构功能函数表达式为Z=g(X1,X2,…,Xn),对应的概率密度函数表示为fx(x1,x2,…,xn)。为方便描述,桥梁的荷载效应用S表示,桥梁的抗力用R表示,R和S是相对独立的随机变量,它们对应的概率密度函数为分别为fR(r)和fs(s),概率分布函数分别为FR(r)和FS(s)
结构功能函数表示为
Z=g(R,S)=R-S
(1)
则失效概率可描述为
(2)
假设由于环境条件影响,桥梁抗力会随着时间的推移而恶化,此时时变抗力R(t)表示为:
R(t)=R0·G(t)
(3)
式中:R0为桥梁服役初始抗力(随机变量),G(t)为抗力衰减函数(随机过程),假设R0独立于G(t)。G(t)=1-a·tα,式中,a和α分别为由试验数据进行拟合分析得到的参数,a为考虑试验数据随机性的随机变量。
桥梁退化的抗力评估中存在偶然不确定性和认知不确定性,偶然不确定性是固有的,不可减少,是自然变异性,如材料特性、几何形状等[4];而认知不确定性可随着认知水平的增加、数据量的增多而减少,如模型不确定性、统计参数不确定等,本式中R(t)和G(t)的选择是认知的。当获取观测数据后,即本文荷载试验历史,可以截断抗力分布的下尾,从而减少来自抗力计算模型和退化模型的认知不确定性。这个方法将在下面介绍。
假设服役时间为T,将T离散为n个时间区间,各个区间内的荷载效应S1,S2,…,Sn互相独立,则(0,T)的可靠性表示为:
L(0,T)=Pr[R(t1)>S1∩R(t2)>S2∩…∩R(tn)>Sn]
(4)
式中:R(ti)表示时间区间(ti-1,ti]的抗力,失效概率表示为Pf(0,T)1-L(0,T)。
2 服役桥梁抗力更新
长久以来随机过程由于其良好的不确定性表征能力而被广泛应用于混凝土桥梁的概率建模。然而现有研究大多集中于初始参数的估计,桥梁实测数据对参数进行更新,实测数据是获取桥梁服役状态的重要依据,因此,本文采用贝叶斯更新方法结合历史荷载信息对抗力进行更新。当服役桥梁进行荷载试验,承受已知荷载时,则抗力的分布在这个已知的荷载效应被简单地截断,根据贝叶斯定理,更新后的抗力分布为
(5)
式中:FS(r)表示时间T内承受的最大荷载效应累积密度函数,FR(r)表示加载前桥梁抗力概率密度函数。
考虑服役期内桥梁抗力随时间退化,假设初始抗力R0的概率密度函数为fR0(r),G(T)的概率密度函数为fG,T(g)。加载前,根据式(3),R(T)的概率密度函数表示为
(6)
考虑到桥梁服役T年,即承受了n个最大荷载效应:S1,S2,…,Sn,根据上文提到的衰减函数,则式(5)可表示为

(7)
式中:FS,i(·)表示时间(ti-1,Ti]内承受的最大荷载效应的累积密度函数,式(7)适用于平稳(FS,i为时不变)和非平稳(FS,i为时变)加载过程。
3 应用实例
3.1 初始抗力计算
文献对欧洲三座实桥荷载试验过程与结果进行了分析,本文以其中一座三跨钢筋混凝土简支T梁桥(12.48+15.96+12.48 m)为例,该桥参照欧洲规范建成于1968年,除去人行道宽度桥宽7 m,主梁T型截面高度为1.3 m,翼板的计算宽度为1.6 m,计算跨径为16.5 m。受拉钢筋初始直径为32 mm,混凝土抗压强度为26 MPa,钢筋屈服强度为335 MPa。
考虑计算模型误差引起的认知不确定性,抗弯承载力可表示为[5]
(8)

通过进行50万次的蒙特卡罗模拟分析,进行K-S(Kolmogorov-Smirnov)检验得到初始抗力近似服从对数正态分布,该分布的统计参数:均值为3 952 kN·m,标准差为454 kN·m。

表1 桥梁抗力和荷载统计参数
3.2 抗力退化评估
进一步考虑钢筋锈蚀的损失,估计当前状态下的桥梁抗力为
(8)
ξs,ξd,ξb分别为考虑锈蚀后钢筋面积、主梁高度、翼板宽度的折减系数,z表示根据条件下抗力评估的修正系数,根据第20年检测评估结果得到ξs=0.85,ξd=0.9,ξb=0.9,z=0.85。因此,计算得到抗弯承载力为2 552 kN·m,与上节计算得到的初始抗力对比得到退化系数为0.646。根据文献[10-12],抗力衰减函数表示为:μ(G(t))=1-0.015 9t,cov(G(t))=0.1。假设恒载效应为固定值,Dn=1 113 kN·m,活载效应L=1 210 kN·m。
该桥在第10年和第15年均进行了荷载试验,重点在于介绍采用贝叶斯方法结合荷载信息进行可靠度评估,包括挠度、应力、应变在内的荷载试验结果,将20年划分为20个时间间隔,考虑荷载试验历史,通过式(7)计算服役一定年限的桥梁抗力更新值,如图1所示。由图可见,服役20年桥梁抗力均值通过荷载试验历史更新后,标准差得以减小,变异系数由0.119减小为0.110,由此可见本文采用的贝叶斯更新方法可结合历史试验数据从而有效减小抗力评估的不确定性。
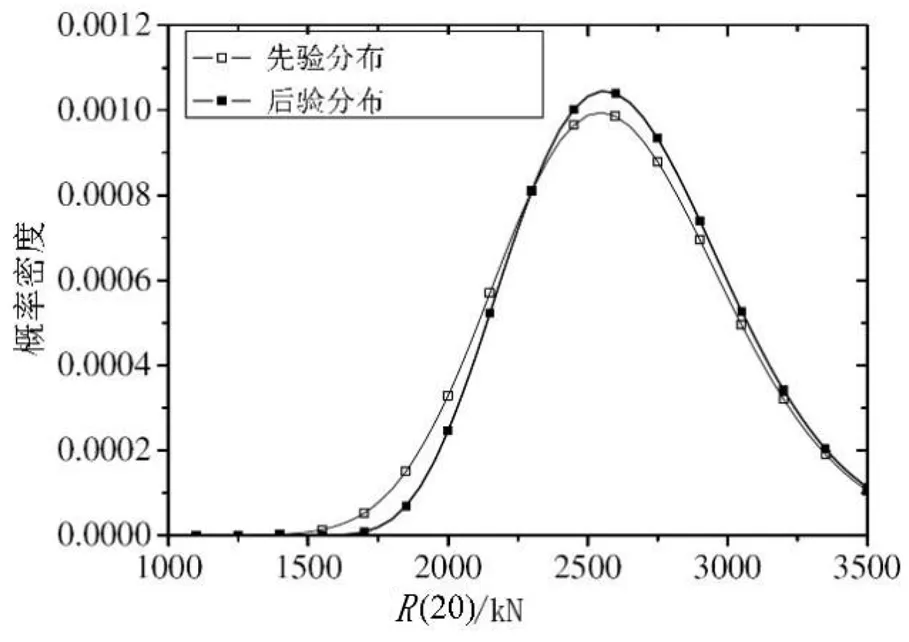
图1 服役20年抗力先验值与更新值对比
此外,计算了荷载历史试验数据更新后的时变可靠指标,如图2所示。从图中可以看出,随服役年限增长,可靠指标不断减小,且更新后的可靠指标明显大于更新前,未考虑第20年条件评估时低估了桥梁的可靠性,证明了本文中结合荷载试验进行抗力更新的必要性,另外,可进一步结合混凝土强度、保护层厚度等日常检测信息进行贝叶斯更新,进而提高可靠度评估精度。本例中采用的抗力更新方法有效结合了桥梁状态评估桥梁,可更真实反映桥梁服役状况,为维修加固决策提供理论指导。
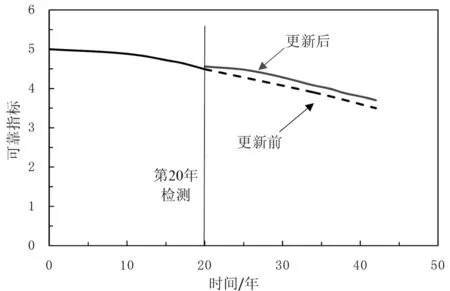
图2 更新前后时变可靠度指标对比
4 结 论
利用历史荷载试验信息并结合贝叶斯方法更新服役桥梁抗力,提出了桥梁时变可靠度计算方法,以一座混凝土实桥为例,演示了抗力更新与时变可靠度评估。服役20年桥梁抗力均值通过荷载信息更新后,变异系数由0.119减小为0.110,减小了抗力评估的不确定性,且更新后的可靠指标明显大于更新前,未考虑荷载信息评估低估了桥梁的可靠性。本研究可为在役混凝土桥梁后期维修加固决策提供理论指导。

