航空复杂结构纤维预制体成型工艺与复合材料性能仿真研究进展*

葛敬冉，刘增飞，乔健伟，梁 军，2

（1. 北京理工大学先进结构技术研究院，北京 100081；2. 北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

先进复合材料具有金属材料无法比拟的低密度、高比刚度和高比强度等特点，在航空航天、交通运输等领域作为主承力结构获得越来越多的应用[1–2]。近些年，随着高端装备性能的提升和先进制造技术的快速发展，为了满足减阻降噪、吸波隐身、耐压抗爆、防隔热一体化等多功能需求，越来越多复合材料复杂 （异形）结构不断涌现[3–6]，如大扭转、变厚度的航空发动机风扇叶片、正负曲率交变的机匣、针刺复合材料飞机刹车片以及各种形态热塑性复合材料角片等在航空领域层出不穷。

目前世界上最先进的航空发动机Leap-X的风扇叶片采用三维机织复合材料制成，在提高发动机性能的同时大幅降低了发动机的重量[7]。叶片是航空发动机中的主要气动部件，为保证气流在叶片上均匀做功，叶片从叶根到叶顶扭角逐渐增大，厚度逐渐减小，外廓尺寸具有大扭转和变厚度的几何形态，在复合材料成型过程中结构内部纱线的走向和形态发生较大变化，见图1[7–8]。Leap-X发动机的机匣也采用机织复合材料制造而成，整个机匣预制件一次编织成型，提高了机匣的耐久性和包容性，从而减少了发动机的维护成本，见图2[9]。发动机机匣在内外法兰过渡区存在正负曲率和厚度的变化，外轮廓具有变厚度和变曲率的几何形态，导致内部织物细观结构发生较大变化。飞机的刹车片、固体火箭发动机喷管结构则采用的是针刺纤维复合材料[10]。针刺复合材料纤维预制体采用专门的倒钩针进行针刺，针刺后纤维发生折断、偏转等损伤，局部微细观结构存在极大的随机性和不确定性，见图3[11]。此外，采用热压快速成型技术制造的角片、支架、加强肋等航空用热塑性复合材料构件同样也存在着复杂的内部特征，如在制造过程中产生的褶皱缺陷、波纹缺陷等，如图4所示[12]。上述航空复合材料结构在预制体赋形过程中发生了纤维的错动、挤压、扭转等，内部纱线形态和走向呈非均匀分布。如何建立真实细观几何结构复合材料性能预示模型，分析复合材料复杂结构力学行为和可靠性，解决目前航空复合材料结构设计主要依靠长时间和高成本试验迭代的现状，对推动航空复合材料复杂结构在航空领域的应用具有重要的工程价值和理论意义。

图2 航空发动机机匣[9]Fig.2 Aero-engine casing[9]

图3 飞机刹车片、喷管制品及针刺预制体形貌[11]Fig.3 Aircraft brake pads, nozzle products and needle punched preform morphology[11]

图4 热塑性复合材料角片及其成型典型制造缺陷[12]Fig.4 Thermoplastic composite angle pieces and typical manufacturing defects[12]

为抑制复合材料结构制造工艺缺陷和快速准确表征评价复合材料结构性能，国内外学者开展了航空复合材料结构制造工艺及性能评价的数值仿真方法研究，以此来缩短其设计周期，降低研发成本，提高结构的可靠性，推动复合材料在航空领域的进一步发展。本文以三维机织和针刺复合材料为对象，从纤维预制体成型工艺过程仿真、细观建模、力学性能分析3方面总结和梳理近年来复合材料及其结构数值仿真方法的研究现状，并为航空复合材料结构数值分析方法提供一种新思路。鉴于复合材料结构的预制体成型方式存在一定的相似性，本文提到的方法也可为其他复合材料及其结构的设计与制备提供参考。

1 复合材料纤维预制体成型工艺过程仿真

复合材料结构的制造过程可以分为纤维预制体赋形和树脂基体固化两个阶段，又称为纤维预制体成型工艺和树脂固化的复合工艺，其中纤维预制体是复合材料的骨架，其成型工艺过程决定了织物结构变化，也最终决定着复合材料的性能。纤维预制体的内部结构由工艺运动学和成型过程中施加在纱线/纤维上的力决定[13]。工艺运动学决定了织物的基本内部纱线结构模式，称为织物拓扑结构。成型过程中施加在纱线/纤维上的力决定了详细的微观几何形状，如纱线截面形状、纱线内的单个纤维路径和纱线曲率。当纤维预制体成型后，再以预制体为增强体将树脂基体浸润固化形成复合材料。复合材料在热固化复合成型过程中，由于材料本身的各向异性、热失配以及基体固化收缩效应等因素，其内部纤维不可避免地会发生一定的运动[14]。但对于织物复合材料而言，由固化成型过程引起的纤维变形很小，基体固化过程对纱线形态、走向的影响可忽略，国内外学者也鲜有研究织物复合材料结构复合工艺过程中的纤维变形行为。在树脂基体固化过程的复合工艺研究方面，国内外学者大多将重点放在了不同固化温度、升降温速率、保温时间、压力以及模具结构形式等对材料残余应力、固化变形的表征方法和模拟方法上[15–17]，涉及树脂流动、相变、传热传质以及热力耦合场分析等诸多内容，也取得较为突出的研究成果。鉴于篇幅所限，本文仅聚焦于复合材料纤维预制体成型过程在数值模拟方法上的进展，而树脂固化成型方面的研究进展不再赘述。

为了反映复合材料内部预制体的微细观几何形态，Wang等[18]首先提出了数字单元法 （DEA）来模拟纤维预制体的工艺成型过程。在该方法中，将纱线看成一个圆形截面的针状连接的杆单元链，纱线之间的接触可以用两个节点的接触来表示。为了避免系统中任意相邻的纱线因平行而造成的全局刚度矩阵的奇异性，在求解数字单元刚度矩阵时采用了刚度扰动法，有

与有限元分析中使用的杆单元的刚度矩阵相同，数字单元的刚度矩阵包括杨氏模量E、横截面积A和元素长度L。Δ用于防止全局刚度矩阵的奇异性（Δ<<1）。然而，由一根纤维组成纱线并不符合实际，比如不能表示纱线横截面的变化，而织物纱线横截面积的变化对渗透率等影响较大。于是，Zhou等[19]对数字单元法进行了改进，提出了多链数字单元方法，将纱线离散成多根纤维组成的结构。当单元长度接近零时，纱线的柔性行为被重现，链变得完全灵活，但这样大大增加了计算时间。为了克服计算效率问题，Miao等[13]提出了一种改进的接触方法。该接触方式允许数字纤维间在长度上接触，这样采用粗大的数字单元网格也能准确地描述织物的微观几何形状，此外，文中还针对多链数字单元方法中存在的两个关键问题 （数字链数量和初始纱线截面形状）进行了研究，发现若采用真实纱线所包含的纤维数量表示数字单元链的数量是不现实的，数字纱线包含19～70根虚拟纤维足以代表真实的纤维束经纬纱线，而纱线中采用更多的虚拟纤维数量只会增加计算时间，对模拟结果的精度无明显提升；另一方面，在多链数字单元分析中，初始纱线横截面的选择并不影响最终的织物形貌[13]。此后，研究者们基于多链数字单元法将制造工艺过程与预制体微观观测联系起来，针对纺织复合材料进行了大量研究，本节将以针刺复合材料和三维机织复合材料为例，介绍数字单元法在纤维预制体成型工艺过程仿真方面的应用。

1.1 针刺纤维复合材料成型工艺过程仿真

针刺复合材料是利用针刺技术，通过刺针对碳纤维布、网胎等纤维复合材料进行接力针刺，把部分面内纤维引入到铺层厚度方向，产生垂直纤维簇，使碳纤维布和网胎相互紧密结合，形成面内和层间均有一定强度的预制体。图5展示了针刺碳纤维复合材料的细观形貌，可以看出针刺碳纤维复合材料具有明显的分层结构，0°、90°无纬布和网胎层交替叠加。材料经过刺针刺入后，部分面内纤维在针刺过程中会被刺针挤压至两侧，部分纤维会在厚度方向发生偏转，呈倒“人”字形[20]。

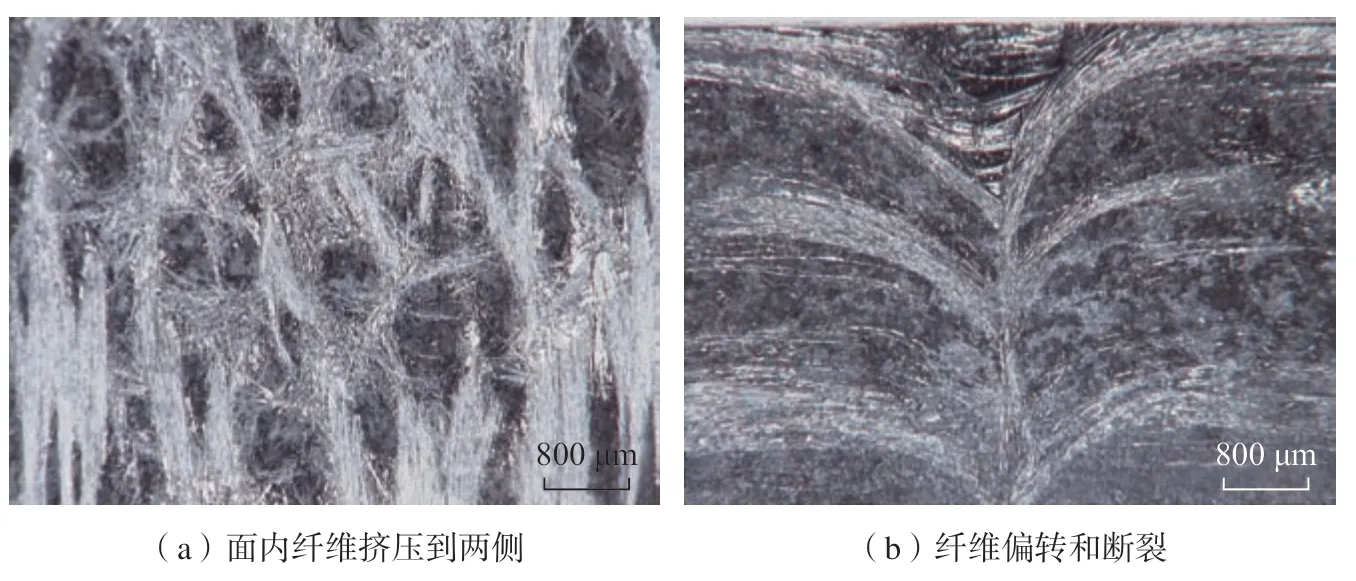
图5 针刺碳纤维复合材料的细观形貌[20]Fig.5 Mesoscopic morphology of needle-punched carbon fiber composites[20]

为精确描述材料局部细观结构、纤维走向和损伤，Xie等[21]建立了二维斜纹石英织物和网胎织物的数字单元模型，采用显式动力学算法对织物层针刺过程进行有限元模拟，模拟结果也得到试验证实，见图6。Song等[22]基于纤维长度和曲率的统计，生成了针刺碳纤维预制体的全尺寸三维数字单元模型，并模拟了预针刺技术的压缩和针刺过程。Yang等[23]则在模拟过程中考虑了纤维束中纤维数量以及捻度，较精确地得到了预制体的微观几何结构变化，如纱线截面变形、经纱卷曲和纬纱移位等，模拟结果与通过Micro-CT获取的细观结构吻合较好。

图6 针刺织物的纤维结构模拟与试验观测结果对比[21]Fig.6 Comparison of simulated fiber architecture and experimental observations of needled fabrics[21]

为了获得优异的材料力学性能，针刺复合材料的制备往往不会一次成型。其制备工艺参数有许多，如针刺密度、针刺深度、布针方式等[24]，甚至有时需要对同一铺层进行多次针刺。为此，Xie等[25]利用参数传递的方法，基于针刺预制体纤维结构形貌特征，划分了4种典型区域，并以此建立了包含这4种区域的周期性单胞模型，分别将计算得到的局部力学性能赋予整体模型中对应的区域，如图7所示，其模型可以分析针刺预制体工艺参数对复合材料有效弹性模量的影响[12]。Han等[26]利用圆弧梁单元和弹簧单元分别描述针刺区域发生偏折的纤维束和基体对纤维束的约束，建立了离散化的针刺C/C复合材料有限元模型，并对该材料的拉伸行为进行了有效预报。

图7 针刺复合材料周期性单胞模型[25]Fig.7 Periodic unit cell model of needled composite[25]

1.2 机织复合材料预制体成型工艺过程仿真

三维机织复合材料是将若干层经纱和纬纱接结在一起，利用多层纱线织造形成三维整体预制体，与树脂基体复合固化而形成的一种新型复合材料。三维机织技术能够制备出各种空间形状复杂的纤维增强预制体，同时，通过空间结构中纤维之间的交点传递和分散载荷，使纤维能以更大限度地发挥纤维增强作用[27]。然而，机织预制件在织造过程中容易发生细观结构变形，纱线走向和截面形态均会在纱线张力和相互挤压作用下发生变化，如图8所示，这些细观结构的变形决定着复合材料的力学性能[28]。

图8 三维机织预制件细观形态[28]Fig.8 3D woven preform mesoscopic morphology[28]

为了能够真实地反映机织复合材料内部预制体结构形态，Green等[29]采用梁单元建立了正交三向织物预制体的数字单元模型，模拟了织物的压实过程，通过与Micro-CT扫描得到的织物压实形态进行对比，模拟结果与试验观测具有较好的一致性，如图9所示。Daelemans等[30]利用数字单元法对拉伸和剪切载荷下三维机织预制体的几何形态和力学行为进行分析，研究发现数字单元法不仅可以准确地描述纱线的几何变形行为，还可以较好地表征预制体的拉伸、剪切力学行为。

图9 Micro-CT扫描图像与数字单元压实模型对比结果[29]Fig.9 Comparison results of Micro-CT scanned images and digital element compaction model[29]

数字单元法可以较好地描述复合材料内部纱线的路径及截面几何形态，但细观模拟计算量大，不适用于复杂预制体结构成型过程模拟。为了解决细观模拟计算量大的问题，研究者们基于连续介质力学，采用唯象本构方程描述预制体的宏观力学响应。彭雄奇等[31]提出了一种超弹性本构模型，描述机织复合材料织物在成形过程中由于大变形所引起的非线性各向异性力学行为。丁纺纺等[32]利用非正交本构模型对机织物半球冲压进行了模拟，取得了好于正交本构模型的模拟结果。预制体宏观模拟方法具有计算效率高，可以与有限元法相结合的优点，但是无法表征复杂结构内部纱线走向和形态的变化，忽略了预制体的细观结构。针对这一问题，目前已有少量工作将宏–细观多尺度模拟方法用于分析预制体变形，得到结构的宏–细观结构特征，但是没有将其应用于复合材料结构的力学性能分析。Iwata等[33]提出了一个宏–细观结合的预制体变形模拟方法，首先采用唯象方法模拟预制体的宏观变形情况，再在预制体的局部通过细观织物力学模型预报纱线的走向以及屈曲情况，整个分析过程计算成本可以接受，如图10所示。Zhang等[34]发展了一种织物增强预浸料的多尺度模拟方法，采用细观单胞模型分析织物的拉–剪耦合效应，通过贝叶斯方法预报纱线性能，形成织物应力模拟器，可以用于预浸料的宏观赋形过程模拟。

图10 织物在半球形模具上悬垂的宏–细观变形模拟结果[33]Fig.10 Results of macro-meso deformation simulation of fabrics draping on hemispherical mould[33]

2 复合材料细观单胞几何建模方法

复合材料的细观几何结构主要指复合材料内部的几何结构，即预制体中纱线之间的相对空间关系。复合材料的数值模拟面临着重要挑战，即如何准确地表示织物的几何形状。考虑到复合材料内部结构在空间上具有一定的周期性，研究者们一般采用细观力学分析方法，通过建立细观单胞或代表体积单元（RVE）来研究复合材料的力学性能。复合材料细观尺度结构由纱线和基体构成，其中纱线由纤维丝束和渗入纤维间的基体组成，为了方便建模，一般采用理想几何的单胞模型来表征复合材料结构。研究人员通过观察扫描电镜、光学显微镜和Micro-CT扫描等切片结果，对纱线进行一定的截面、路径假设，从而通过参数化的方式创建材料细观结构理想模型。纱线的横截面形状一般假设为圆形、椭圆形、跑道形、凸透镜形等，且不受纱线相互挤压、扭转等影响，截面形状保持不变。Cao等[35]基于Micro-CT扫描图像对经纬纱的截面分别进行了假设，建立了三维机织复合材料实体几何单胞模型。Song等[36]将纤维束截面假设为矩形和凸透镜形，并考虑到三维机织复合材料在不同区域的挤压程度，分别建立了复合材料的表面单胞和内部单胞模型。Fang等[37]假设纤维束截面为八边形，采用随机函数理论表征了编织复合材料因扭曲造成的随机弯曲路径。但理想几何模型多用于低纤维体积含量的复合材料，当纤维体积含量较高时，由于纱线间的相互挤压变形会导致纱线具有不同的波纹度且纱线截面存在一定的非对称性和扭转。理想几何模型所假设的规则纱线形态、轨迹与真实模型差距较大，甚至纱线几何模型会出现一定的干涉，无法满足力学性能分析的需要。刘增飞等[38]通过研究发现机织复合材料实际细观结构与理想细观结构相比，其细观纱线具有明显不同的卷曲程度，且纱线的卷曲程度对复合材料的拉伸力学响应（如“台阶”效应）有较大影响，如图11所示。为了能够精确描述复合材料内部细观纱线的真实几何结构，学者们发展了两种主要的建模策略，一种是基于Micro-CT图像处理技术的建模方法；另一种为基于预制体工艺仿真成型技术的重构方法。

图11 三维机织复合材料细观纱线对比及其拉伸力学响应[38]Fig.11 Comparison of mesoscopic yarns and tensile mechanical response of 3D woven composites[38]

2.1 基于Micro-CT图像的重构方法

随着Micro-CT技术的发展，其在材料内部结构表征和无损检测等领域的应用越来越广泛。采用Micro-CT扫描技术建立的几何重构模型可以表征复合材料的细观尺度结构，描述结构内部纱线的真实形态，避免了理想化假设，能够反映影响织物结构的任何微观变化。Faes等[39]通过手动提取 Micro-CT 切片图像内纤维束的截面轮廓，建立了机织复合材料的有限元模型，如图12所示。Naouar等[40]采用图像分割的纹理分析方法对Micro-CT图像进行处理，分割经纱、纬纱和粘合纱，自动建立了三维织物的细观尺度有限元模型。Huang等[41]提出了“Micro-CT辅助几何建模”的新方法来重构三维机织复合材料的详细几何模型，并通过引入新的多因素形态学准确性标准来评价重构的几何模型。Fang等[42]基于Micro-CT扫描切片图像，利用滤波、收缩等方法自动识别出了纱线的截面轮廓，并将纱线截面信息转化为点云数据，空间几何重构出了三维编织复合材料细观精细化模型。然而，基于Micro-CT图像的重构方法需要在制得织物预制体或复合材料后才可以进行扫描建模，且只能研究现有结构，生成的实体单元结构复杂，转化为有限元分析模型时增加了网格划分的难度。同时，Micro-CT扫描成像质量受结构尺寸影响较大，无法对整个复杂结构内部纱线的细观形貌进行观测。

图12 Micro-CT扫描重构建模[39]Fig.12 Micro-CT scan reconstruction modeling[39]

2.2 基于预制体工艺成型数字化仿真的重构方法

一般来说，预制体被模具压实赋形后，树脂基体固化过程对纱线形态、走向的影响可忽略，即复合材料结构具有和赋形后预制体相同的细观结构。正如1.2节所介绍的，数字单元法可以模拟预制体成型工艺过程，有效地预报预制体的纱线走向及截面形态。然而，预制体成型工艺过程仿真结果由一系列相互连接的杆/梁单元组成，并不能直接用于复合材料的力学性能分析，因为在细观尺度下，纱线需要定义为实体几何。Huang等[43]采用滚圆在虚拟纱线横截面上逆时针滚动获得了纱线截面轮廓周长，并通过连接纱线截面周长上的对应点生成了细观纱线表面。Green等[44]提出了一种修正的凸胞算法来生成虚拟纱线的截面形状，并利用提取出的纱线截面信息几何重构生成了机织复合材料细观真实模型。Liu等[45]考虑到纱线存在一定的扭曲，利用Alpha-shapes算法和数字单元链追踪法准确提取了虚拟纱线的截面信息，精确构建了细观纱线的几何形状，如图13所示。通过与真实试样的截面形状和纱线路径进行对比，如图14所示[45]，有效地验证了所建细观几何模型的准确性，在此基础上作者采用精细化模型和理想模型预报了机织复合材料的拉伸力学性能，发现采用精细化模型预报的应力–应变曲线与试验结果更加吻合。采用这种建模方法能够较精确地体现复合材料的细观几何特征，但也存在一些缺点，对于多层连接结构适用性比较好，对于采用编织、针刺等结构不是特别适用。

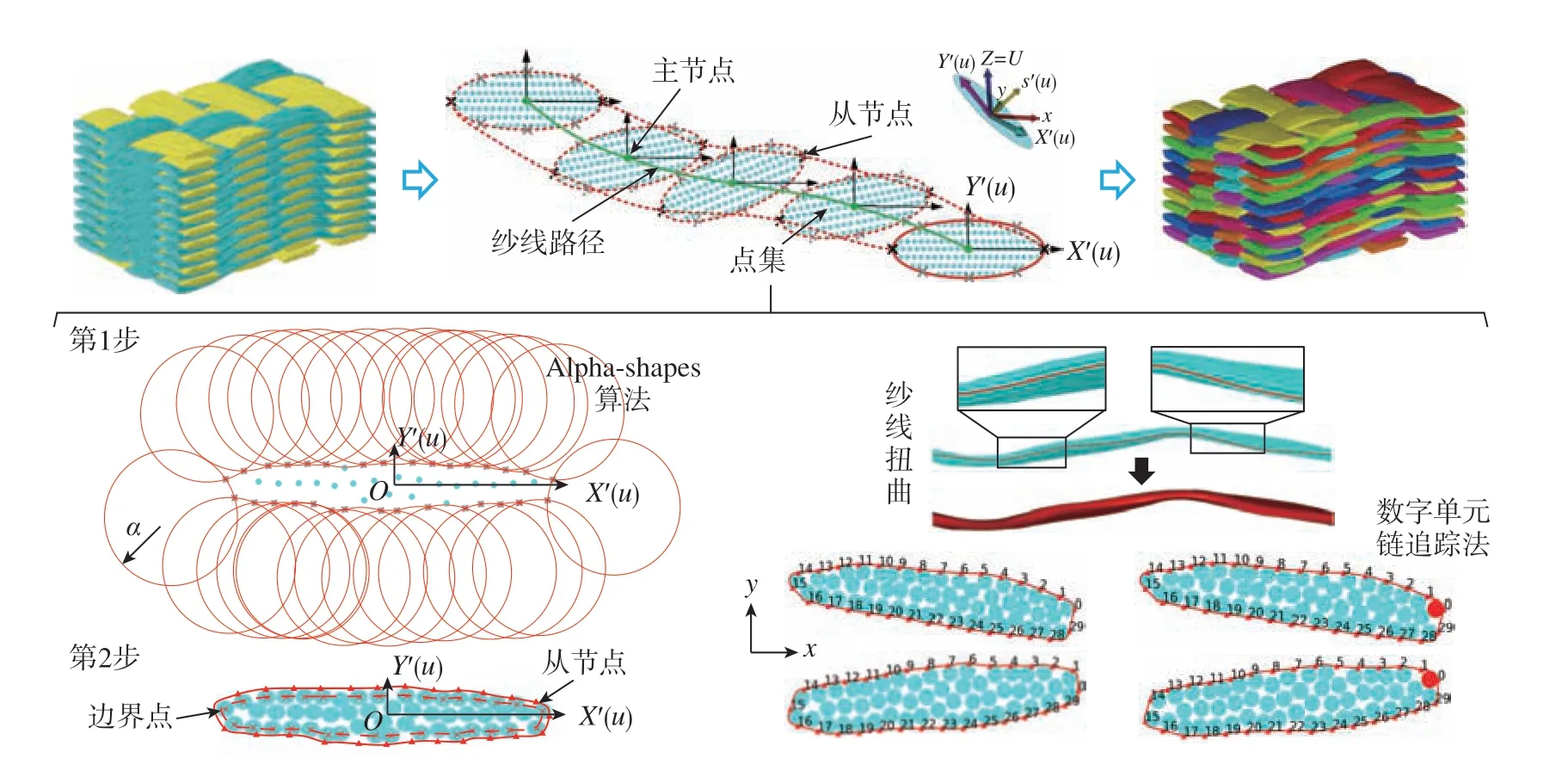
图13 基于预制体仿真成型结果的重构建模[45]Fig.13 Reconfiguration modeling based on preform simulation molding results[45]

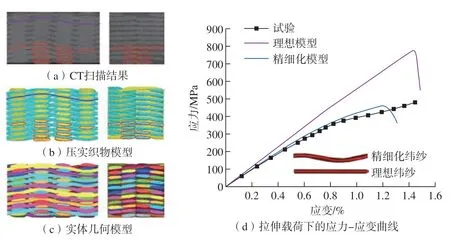
图14 复合材料细观模型几何形态与力学性能试验验证[45]Fig.14 Experimental verification of geometry and tensile mechanical properties of composite mesoscopic model[45]

3 复合材料力学性能的数值分析方法

针对复合材料结构的力学性能研究方法包括试验方法、解析分析方法以及数值分析方法。试验方法所需时间周期长、制造成本高，且存在不可避免的局限性。基于理论的解析模型无法准确捕捉到材料内部的应力特征，只能预报一些具有简单规则细观结构复合材料的刚度性能[46–48]，难以预报复合材料的强度性能。随着计算机技术和有限元等数值方法的快速发展，越来越多的学者更趋向于采用数值分析方法研究复合材料及其结构的力学行为。

复合材料结构具有天然的多尺度特性，从微观尺度的纤维束到细观尺度的复合材料单胞，再到宏观尺度结构件，不同尺度具有不同的结构特征。由于复合材料结构的内部特征非常复杂，直接对其进行求解难度较大。为了简化问题，考虑到复合材料结构在细观、微观尺度上一般呈周期性排列，由重复排列的RVE组成，通过求解RVE模型可得到复合材料在微–细观尺度的等效力学响应，目前常用的单胞模型的求解方法有直接数值模拟方法以及缩减模型方法。但仅在微–细观单胞尺度下对复合材料结构的力学响应进行合理预报仍是不充分的。因此，研究者们提出了多尺度的概念，通过建立宏观结构与微–细观结构之间的联系，利用微–细观RVE的力学响应来预测宏观性能，常用的方法有层级多尺度、子区域多尺度和并发多尺度方法。

3.1 代表性体积单胞模型的求解方法

随着计算力学与高性能计算集群的发展，直接数值模拟成为一种有效求解单胞模型的方法。目前使用较为广泛的直接数值模拟方法包括有限单元法 （FEM）和快速傅里叶变换法 （FFT）。值得注意的是，对于复合材料力学性能数值模拟的计算精度和速度而言，网格离散是一个关键步骤。特别是对复合材料复杂细观几何结构来说，即使采用四面体进行离散也很难得到与内部细观结构相界面一致光滑的网格[49]。采用体素网格离散技术则很好地解决了这个问题，能够对任何复杂的结构进行网格划分。体素单元根据其中心的位置来界定不同的材料相。但体素网格不能够得到光滑的相界面，为此，研究者们提出了非均匀体素网格离散技术[50]和应力平均化技术[51]来有效地缓解界面处的阶梯状体素单元边界造成的局部应力集中现象。在此基础上，很多研究者利用FEM或FFT方法，结合刚度折减法或连续介质损伤力学，建立了纺织复合材料单胞的渐进损伤分析模型。Fang等[37]采用Murakami-Ohno损伤理论，利用FEM方法研究了三维编织复合材料单胞在拉伸载荷下的渐进损伤过程。Zhong等[52]利用FEM方法研究了纱线波动对三维机织复合材料面内刚度和强度的影响。Jia等[53]利用FEM方法分析了三维机织复合材料的非线性黏弹性损伤过程。Ge等[54–55]采 用Matzenmiller损伤理论建立了细观组分材料的耦合弹–塑性损伤模型，利用FEM方法研究了三维编织复合材料的非线性力学行为，如图15所示。Liu等[45]采用体素网格离散了三维机织复合材料精细化模型，利用FEM方法预报了机织复合材料的拉伸力学性能。FEM方法在计算单胞模型的等效刚度和强度性能，分析其失效行为时表现出了较高的准确性，但由于复杂细观结构的单胞模型需要很大数量的网格来离散，无法避免地导致计算量的增加。FFT方法是一种基于离散像素点的快速计算方法，通过对每个离散像素点的应变做迭代求解，在傅里叶空间对应变进行更新，在实空间对应力进行更新，从而快速求解单胞的力学响应。相较于FEM方法，FFT方法无须进行单元插值及刚度组集，故计算效率得到较大提高，通常是FEM方法的数十倍。田晓晓[56]采用FFT方法研究了复合材料的力学性能及细观损伤机制。Wang等[57]使用FFT方法研究了三维编织复合材料的渐进损伤行为，如图16所示，FFT方法对于组分性能差异大以及具有复杂微观结构的单胞模型，其算法收敛性较差且计算量仍然较大。

图15 基于FEM的复合材料单胞分析方法[55]Fig.15 Composite unit cell analysis method based on FEM[55]

图16 基于FFT的复合材料单胞分析方法[57]Fig.16 Composite unit cell analysis method based on FFT[57]

FEM方法和FFT方法都是对单胞模型高分辨率、高精度的计算方法，必然会导致较大的计算量，影响计算效率。为了提高单胞模型的求解效率，研究者们提出了各种缩减模型方法。Dvorak等[58]提出了TFA（Transformation field analysis）方法，假设每一组分材料内的变量均匀，并通过叠加原理来求解每一组分的变量，通过对求解单胞进行分块，从而降低了求解的自由度，但该分块策略较粗糙，难以捕捉界面处的应力集中等现象。Michel等[59]进一步改进了TFA方法，假设每一组分的变量场非均匀且每一组分可以分为多个区域，但分块区域内的非均匀性需要高精度有限元来表征，增加了计算的自由度与复杂性，从而降低了计算效率，难以应用于具有复杂细观结构的单胞模型。Liu等[60]最近提出了基于数据驱动的自洽聚类分析 （SCA）方法，该方法使用离线–在线两阶段策略，其中离线阶段使用基于数据驱动的聚类分析算法实现模型的缩减，在线阶段求解缩减模型的离散Lippmann-Schwinger方程，在保证求解精度的同时，大大提高了计算效率。基于这种思路，Tang等[61]提出了虚拟聚类分析 （VCA）方法，从数学角度对SCA方法的收敛性进行了分析并提出了相互作用张量的快速计算方法。Cheng等[62]基于有限元理论框架提出了有限元聚类分析 （FCA）方法，其中相互作用张量采用有限元计算而非借助格林函数。He等[63]发展了考虑各向异性损伤的SCA方法，并采用SCA方法和有限元方法分别模拟了三维编织复合材料在单轴拉伸载荷下的损伤演化过程，如图17所示，SCA方法预测的复合材料强度与试验结果的误差在5%以内，但其计算效率约为有限元方法的近千倍。

图17 基于数据驱动的SCA分析方法[63]Fig.17 SCA analysis method based on data-driven[63]

3.2 复合材料结构的多尺度分析方法

针对复合材料结构的多尺度特征，部分学者在预报复合材料结构力学性能时采用均匀化理论，用均匀化一个单胞之后的力学性能代表宏观结构各材料点的力学响应，实现各尺度之间由下而上的均匀化逐级单向传递，研究者们称此方法为层级多尺度方法。Potluri等[64]采用这种层级多尺度方法预测编织复合材料管结构的力学性能。He等[65]也基于该方法分析了编织复合材料结构在高温下的拉伸、弯曲力学性能。Bassam等[66]将一系列周期性单胞模型的均匀化响应作为输入信息赋予复合材料设计空间中指定位置，结合宏观尺度和细观尺度对二维平纹编织复合材料层合扭曲板进行弹性静力响应分析，如图18所示。这种基于均匀化的方法虽然计算效率较高，但需在各个尺度分别建立本构关系独立计算，尺度之间没有耦合，无法考虑尺度之间的相互作用。此外，对于航空复合材料复杂结构，其内部细观几何结构高度不均匀，结构各部位的代表性体积单胞各不相同，采用这种方法预测复合材料复杂结构力学性能将产生较大误差，而且不能有效地揭示复杂结构各尺度下的失效模式。

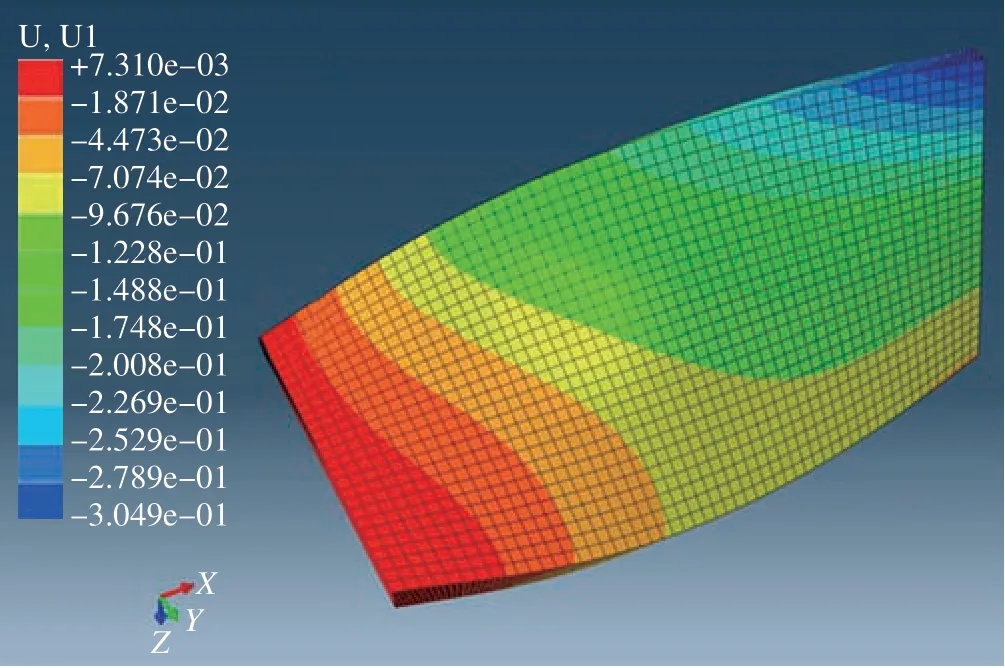
图18 基于均匀化模型的扭曲板位移响应[66]Fig.18 Displacement response of twisted plate based on homogenization model[66]

为了综合考虑复合材料复杂结构内部损伤破坏分析的精确性与多尺度计算模型的效率，部分研究者提出了子区域微结构的多尺度方法，将不同尺度的计算模型放置于同一个求解模型中，即在危险区域建立具有微观结构信息的模型，而在其他区域建立宏观模型。Hettich等[67]将细观结构作为子结构嵌入到复合材料平板模型中，模拟了损伤在细观结构中的萌生与扩展。Marfia等[68]将微观单胞按微观结构分布特征划分成多个子区域，微观的力学响应进行体积平均得到宏观物理量，并采用了预测–校正技术，研究了弹塑性或黏塑性复合材料结构的力学响应，分析过程如图19所示。基于子区域的多尺度计算方法需要人为划定危险区域，且宏观均匀区域的材料性能需要预先定义本构方程计算，并非实时双向多尺度模拟。

图19 复合材料微观单胞子区域的多尺度模拟方法[68]Fig.19 Multiscale simulation method for microscopic unit cell subregion of composites[68]

并发多尺度方法则借助均匀化方法来实现不同尺度之间的耦合。在该方法中，需要两套求解方法分别对宏观与细观结构进行求解。Feyel等[69]提出了基于FE2的多尺度计算方法，在宏观结构每个单元的高斯积分点耦合一个细观单胞模型，两个尺度都使用有限元法进行求解，并通过与全尺寸细观模型的FEM结果对比，验证了FE2多尺度计算框架的可行性。Tikarrouchine[70]、Tchalla[71]、Xu等[72]使用FE2方法模拟了复合材料的非线性力学行为，但其所选微观与细观结构较为简单，且使用少量的单元数对细观、宏观结构进行离散。由于FE2多尺度方法在细观尺度上采用有限元法进行计算，导致整个多尺度计算效率较低，难以应用于具有复杂细观结构复合材料的多尺度分析。Spahn等[73]提出了FE–FFT的多尺度计算方法，即在细观尺度使用计算效率相比FEM高的FFT，并将细观尺度计算结果均匀化后返回到宏观尺度的有限元计算中，如图20所示。Fang等[74]使用FE–FFT方法模拟了复合材料的拉伸及弯曲失效行为。Wang等[8]将不确定性量化模型嵌入到FE–FFT 的多尺度计算方法中，在宏–细–微观各尺度内进行不确定性量化，并在不同尺度间进行传递，揭示了编织复合材料扭曲异形结构在悬臂梁载荷条件下的损伤失效机理，分析流程如图21所示，但其收敛性较差、计算量仍然较大，难以实现宏观结构与细观结构的全耦合计算。Dvorak等[75]则建立FE–TFA多尺度方法，并应用于复合材料的弹塑性行为分析中，表现出较高的计算效率，但停留于算法发展及弹塑性验证，尚难以应用于具有复杂细观结构的复合材料及结构多尺度分析中。对于新发展的SCA方法，鉴于其求解复杂单胞时的高效性，可有效应用于多尺度分析中。Liu等[76]通过在宏观有限元模型中每个单元高斯积分点耦合一个SCA计算的细观单胞模型，采用FE–SCA方法研究了三维双开孔复合材料板的非线性力学行为，如图22所示。Han等[77]基于FE–SCA多尺度方法研究了平纹编织复合材料的弹塑性力学行为，验证了基于SCA方法多尺度方法的高效性。He等[78–79]提出了基于数据驱动的编织复合材料与结构并发多尺度聚类分析算法SCA2和FE–SCA2，避免了宏–细–微观不同尺度之间双向耦合导致的维度灾难问题，实现了三维编织复合材料与结构多尺度损伤与失效的分析与评价，如图23所示。目前基于SCA方法的多尺度分析集中于均匀宏观结构的弹塑性分析，即宏观结构不同位置对应的微细观单胞相同，亟须将其发展并扩展到非均质复杂结构的多尺度损伤分析中。

图20 复合材料FE–FFT多尺度计算方法[73]Fig.20 FE–FFT multiscale calculation method of composites[73]

图21 基于不确定性量化的FE–FFT多尺度方法示意图[8]Fig.21 Illustration of FE-FFT multiscale method based on uncertainty quantification[8]

图22 基于FE–SCA多尺度方法的双缺口复合材料板力学行为[76]Fig.22 Mechanical behavior of double-notched plate composite plates based on FE–SCA multiscale method[76]

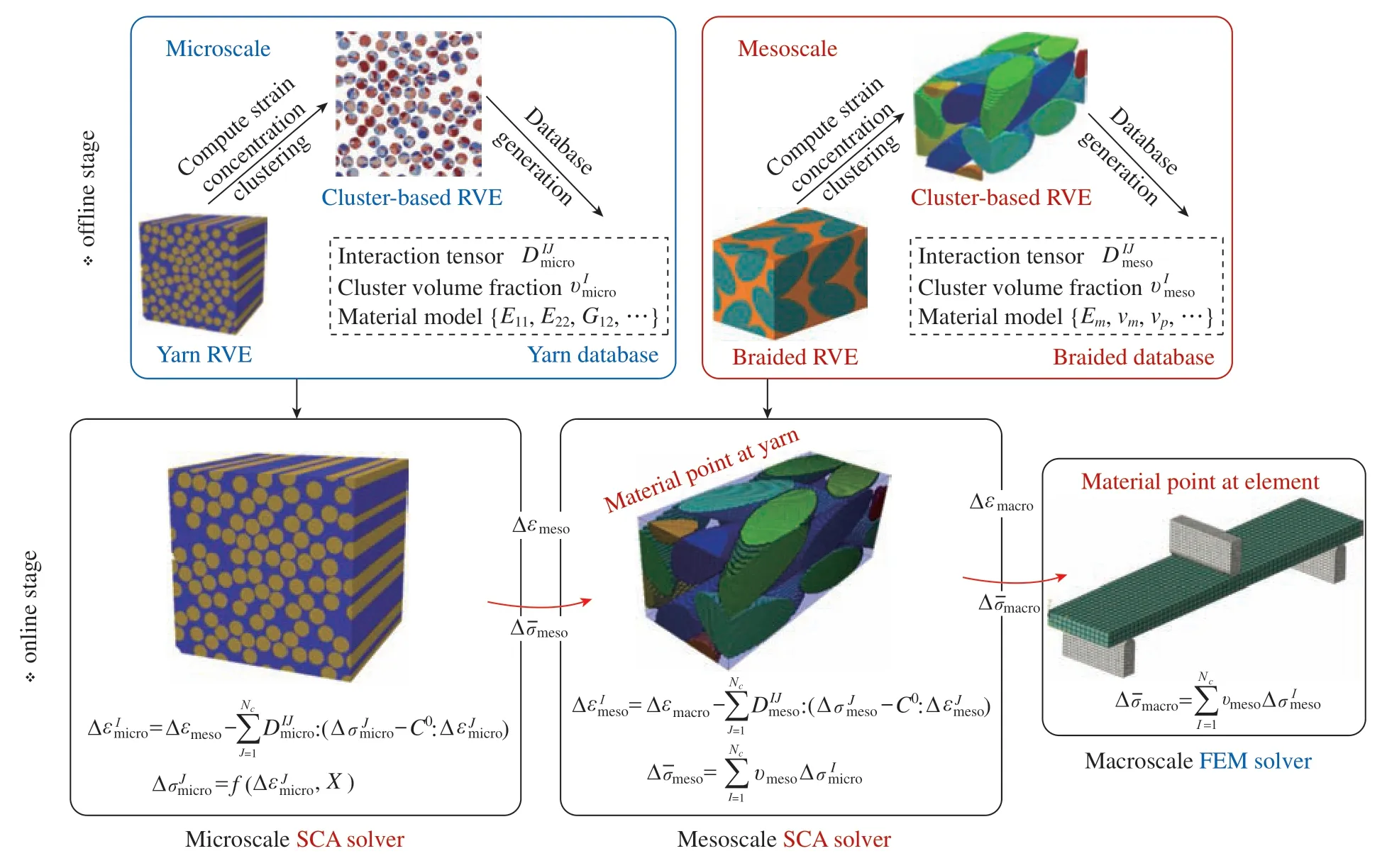
图23 编织复合材料结构的宏–细–微观耦合FE–SCA2并发多尺度框架[79]Fig.23 Schematic of concurrent three-scale FE–SCA2 scheme for braided composites[79]

前述的方法在求解宏观结构力学响应的时候，需要反复求解单胞模型，而如果使用机器学习方法计算单胞模型的力学响应，则可以更为高效地进行多尺度计算。Le等[80]将神经网络 （NN）用于训练细观结构的响应，并搭建了FE–NN多尺度框架来预测宏观结构的响应。Yang等[81]同样运用神经网络算法训练样本数据以得到对应的非线性弹性本构关系，并应用于宏观结构分析。Liu 等[82]提出了“深度材料网络”的多尺度建模方法，通过机器学习将多相组分材料均匀化解析解连接组合得到复合材料的复杂力学响应，保留了复合材料单胞模型部分细观结构拓扑信息和力学响应机制。Xu[83]、Tang[84]等也基于数据驱动或机器学习算法进行了复合材料多尺度分析方法的相关研究。基于神经网络的多尺度计算，细观单胞模型的力学响应由已训练的数据库插值得到，线上计算时存在数值外推的风险，在处理非线性响应时往往精度不够，且只能给出单胞的均匀化结果，无法描述单胞的细观结构拓扑信息和组分材料的力学响应机制。另外，如果单胞细观结构改变，需要重新生成训练数据库，使得计算量巨大。因此，需要发展包含物理响应机制和细观结构特征的机器学习方法，应用到航空复杂结构力学性能的多尺度分析中。

目前基于均匀化的多尺度分析方法存在计算量大，难以表征结构的宏–细观损伤过程等缺点；基于机器学习的多尺度分析方法计算效率高，但无法准确描述材料的力学响应机制。此外，航空复合材料复杂结构在制造过程中内部纱线细观结构发生较大变化，细观尺度上具有高度的非均匀性，结构各位置的细观RVE各不相同，目前多尺度分析均假设宏观结构不同位置对应的细观RVE相同，无法描述复合材料复杂结构件的真实细观结构，难以准确分析结构的非线性力学响应。因此，亟须将预制体成型工艺过程仿真与高效多尺度分析方法相结合，通过纤维预制体成型工艺过程数值仿真得到复杂结构内部的细观结构，建立数据驱动的高效多尺度分析方法，揭示复杂结构成型工艺过程–细观结构–结构服役性能之间的映射关系，从而抑制复杂结构制造缺陷，优化制造工艺方案，提升产品质量的稳定性和可靠性，如图24所示。

图24 航空复合材料复杂结构的制造工艺与力学性能研究框架Fig.24 Research framework of manufacturing process and mechanical properties for aeronautical complex structures of composites

4 结论

本文通过总结和评述复合材料结构制造工艺及力学性能仿真研究进展，对复合材料及其结构研究的现状和未来发展趋势总结如下：

（1）航空复合材料复杂结构在预制体赋形过程中内部细观纱线发生变形，使得结构内部细观几何结构高度不均匀。Micro-CT扫描方法可以表征复合材料内部细观纱线的走向与形态变化，但是无法对整个复杂结构内部纱线的细观形貌进行观测。基于宏观唯象本构的预制体变形模拟方法计算量小，可以模拟预制体宏观变形，但是无法表征复杂结构内部纱线走向和形态的变化；细观模拟方法可以模拟复合材料内部纱线走向和形态的变化，但是计算量大，无法对预制体结构进行变形过程分析。因此，亟须发展航空复合材料复杂结构预制体成型工艺的宏–细观仿真方法，得到复杂结构赋形后内部纱线的形态和走向变化，建立其细观结构的数字化表征手段。

（2）目前基于均匀化的多尺度分析方法存在计算量大，难以表征结构的宏–细观损伤过程等缺点；基于机器学习的多尺度分析方法计算效率高，但无法准确描述材料的力学响应机制。基于缩减模型SCA的多尺度分析方法在复合材料结构的多尺度分析中表现出了极高的计算效率，实现了结构的多尺度损伤分析与评价，但是研究均集中于宏观均匀结构。而航空复合材料复杂结构在细观尺度上表现出高度的不均匀性，结构各部位的细观RVE各不相同，且存在随机不确定性，因此亟须将数据驱动的缩减模型方法拓展到复杂结构的多尺度损伤分析中，高效准确地分析和评价复杂结构的力学性能。

（3）航空复合材料复杂结构的力学性能与预制体成型工艺过程密切相关，亟须将预制体成型工艺过程仿真与高效多尺度分析方法相结合，建立复合材料复杂结构预制体成型工艺过程–细观结构–宏观结构力学性能的映射关系，为优化航空复合材料复杂结构工艺方案，提升质量的稳定性和可靠性提供重要理论基础和技术支撑，从而推动其在航空领域的应用。