模块化功率变换器驱动开关磁阻电机转矩控制

杨广辉，郭振超，程启原，黄晓灿

(1.国家知识产权局 专利局，北京 100088；2.洛阳电光设备研究所瞄准显示部，洛阳 471000；3.西北工业大学 自动化学院，西安 710072；4.吉林大学 通信工程学院，长春 130022)

0 引 言

开关磁阻电机(SRM)驱动系统具有结构简单、工作可靠、机械强度高、高效节能、调速精度高、起动电流小、可频繁正反转运行等优点[1]，在航空航天、电动汽车、家用电器、工业传动等领域具有广泛的应用前景[2-5]。不对称半桥功率变换器是SRM驱动系统中常用的功率变换器拓扑[6]，不对称半桥功率变换器通常由分立的功率开关器件和二极管，或者电源斩波模块搭建而成，不采用工业上成熟的电机驱动功率模块，这无疑增加了系统的复杂度与成本。

文献[7]提出的模块化功率变换器由1个半桥IGBT模块和1个三相全桥IGBT模块组成，电机相绕组采用星形连接并将中线引出，减少了电机与功率变换器的接线数量，提高了系统的可靠性。文献[8]针对文献[7]无法实现重叠导通的缺陷，提出了新型双极性励磁控制策略，该方法改善了模块化功率转换器的控制性能，提高了电机输出转矩，增加了功率变换器的灵活性和适用性。

在抑制SRM转矩波动领域，直接瞬时转矩控制(以下简称DITC)具有很好的应用前景。文献[9]采用的SRM DITC控制方法，提出了在不同工作区域内对转矩误差分别进行补偿的方案，并根据变化的工作条件动态调整换相时刻，通过转矩误差调节器和检测相电流结束的时刻，在每个电周期内修改开通角和关断角。文献[10]提出了一种基于电流重叠角可变的转矩分配函数对DITC方法进行优化。文献[11]引入了脉宽调制(PWM)来调制转矩偏差，代替传统DITC中的转矩滞环控制器，根据PWM信号和转子位置所在的扇区选择最佳开关信号，根据转矩特性曲线，分析了换相期间的转矩脉动，提出了补偿方法。

本文采用文献[8]中的模块化功率变换器拓扑结构，在传统DITC策略的基础上，提出了一种基于电流重叠角优化和脉宽调制的DITC方法，将传统转矩分配函数中固定的电流重叠角替换为实时计算的值，并在转矩控制器设计时结合脉宽调制算法，有效降低了SRM的转矩脉动。

1 SRM模块化功率变换器转矩控制策略

本文采用的模块化功率变换器拓扑如图1所示，由1个三相全桥开关模块和1个半桥开关模块组成，其相电流是双极性，每个工作模式下存在2种不同的运行状态。

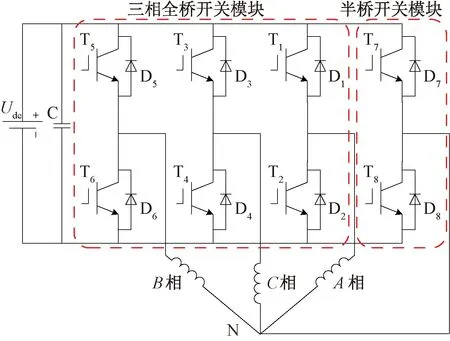
图1 模块化功率变化器拓扑结构

模块化功率变换器驱动的DITC原理框图如图2所示，采用双闭环控制，根据位置传感器得到转速n后与参考转矩nref进行比较，得到参考转矩Tref，利用静态转矩特性得到当前瞬时转矩T，与参考转矩Tref比较后经DITC转矩控制器得到开关信号。

图2 DITC原理框图

转矩控制器的设计是SRM DITC的核心，其中滞环控制方法是应用较多的偏差控制方法，滞环控制器结构相对简单，应用范围广。将模块化功率变换器工作模式分别定义如下：励磁模式为“1”状态，续流模式为“0”状态、退磁模式为“-1”状态。模块化功率变换器转矩滞环控制原理如图3所示。

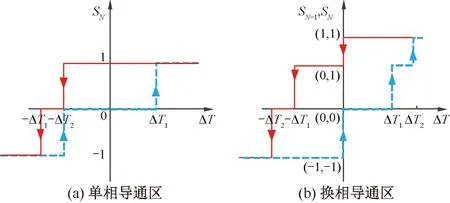
图3 模块化功率变换器转矩滞环控制原理图

图3中，转矩误差ΔT定义：

ΔT=Tref-T

(1)

ΔT1和ΔT2分别为转矩滞环的内环带宽与外环带宽。

在单相导通区，转矩滞环控制原理如图3(a)所示，以A相为例，如果其初始状态为“1”，A相绕组通过开关管T1和T8施加+Udc母线电压，电机输出转矩快速增大，转矩误差ΔT快速减小。直至转矩误差小于-ΔT1时，改变绕组状态为“0”，此时A相绕组处于续流阶段，转矩误差继续缓慢减小到-ΔT2，此时电机输出转矩过大，需要退磁以减小电磁转矩，满足系统需求，即改变绕组状态为“-1状态”，给A相绕组施加-Udc母线电压，电磁转矩快速减小。

在换相导通区，转矩滞环控制原理如图3(b)所示，以A、B两相重叠导通为例，且A相为开通相，要建立转矩，而B相处于关断角前期，由于模块化功率变换器存在电气耦合，每相并不独立，此时需要对这两相的开关状态同时进行调节，其中SN-1、SN分别代表退磁相和励磁相。

若A、B两相的初始状态分别是(1, 1)，电机输出转矩快速增大，转矩误差ΔT快速减小到0，为保证总转矩稳定，牺牲退磁相，使B相绕组处于续流状态，励磁相A相绕组建立转矩保持不变，即选择状态(1, 0)。当转矩误差ΔT达到内环下限-ΔT1时，此时选择状态(0, 0)，A、B两相均处于续流状态，实际输出转矩增加缓慢；直到转矩误差ΔT达到外环下限-ΔT2时，表明电机输出转矩远大于参考转矩，需要关断开关管T1、T6，绕组处于退磁状态，电机输出转矩减小，以维持转矩稳定。

2 电流重叠角优化和脉宽调制DITC策略

2.1 电流重叠角优化的转矩分配函数设计

转矩分配函数(TSF)控制策略是以合成瞬时转矩保持恒定为目标，通过转矩分配函数分配各相绕组在不同位置时的预期转矩。常用的转矩分配函数有直线型、指数型、余弦型以及立方型4种。

本文采用余弦型转矩分配函数进行转矩分配，其函数表达式：

(2)

式中：θon为开通角；θoff是导通相按照转矩分配函数设定的规律开始减小分配的电磁转矩的起始位置角；θov是相邻两相电流重叠导通的角度；τr为电机转子角周期。

(3)

转矩分配函数与开通角、关断角以及电流重叠角有关，传统转矩分配函数将电流重叠角θov定义为常数，但设定恒定的θov并不能严格保证SRM各相分配函数之和一直为1，从而产生较大的转矩脉动。

SRM电流重叠角在不同工况下的变化如图4所示。图4中，iB_TSF、iA_TSF分别为转矩分配函数中电流重叠角θov_TSF不变时，对应的B、A相绕组电流；iB为实际工况下B相绕组电流，θov为实际工况下电机电流重叠角。

图4 电流重叠角变化示意图

当电机低速或者带较小负载电动运行时，相电流较小，如图4(a)所示，当SRM从B相换相到A相运行时，实际的电流重叠角θov<θov_TSF，按照传统的余弦型分配函数，在S1区域内应满足式(4)，但此时B相无法产生转矩，实际转矩分配如式(5)，因此电机实际产生的电磁转矩小于转矩分配函数分配的电磁转矩。

(4)

(5)

当电机高速或者带大负载运行时，相电流较大，如图4(b)所示，当SRM从B相换相到A相，实际的电流重叠角θov>θov_TSF，若按照传统的余弦型分配函数，在S2区域内应满足式(6)，但是B相仍可以产生转矩，实际转矩分配如式(7)，因此电机实际产生的电磁转矩将会大于转矩分配函数分配的电磁转矩。

(6)

(7)

针对上述问题，本文采用电流重叠角可变的转矩分配函数来对传统的DITC策略进行改进。以A、C相重叠导通为例，电流重叠角θov=θA0-θonC。其中θonC为C相开通角，θA0需要实时在线检测，在θA0处，理论上A相电流满足下式：

(8)

通过检测相电流大小和变化率可以计算得到实际电流重叠角θov的值，将实时计算所得的θov代替传统余弦型转矩分配函数中固定的θov_TSF。

2.2 结合PWM的转矩滞环控制器设计

在SRM DITC算法中，转矩控制器采用传统滞环控制方法，结构简单，但滞环限设置的大小会影响到滞环控制方法的效果。当滞环限范围设置得比较小时，虽然可以提高系统的响应速度，但是无疑增加了功率开关器件的负担，在开关频率比较高的情况下可能会导致功率器件开关无法响应，会引起系统失控的严重后果；当滞环限设置得比较大时，系统的控制作用就会减弱，不能达到抑制转矩脉动的目的，并且在滞环限内系统功率开关器件不动作，于是系统进入到了一种“自由响应”阶段。

为了克服传统滞环控制方法滞环限内不动作、滞环限外强制动作的缺点，本文在模块化功率变换器的基础上，结合PWM算法进行转矩滞环控制器设计，在滞环限内采用PWM算法，在固定采样周期下连续调整转矩误差，在滞环限外部采用传统滞环控制方法。PWM调制方法定义如表1所示。

表1 调制方法定义

在一个采样周期Ts内，定义转矩误差采样值为ΔTsample，δ为误差阈值的绝对值，本文将滞环限之间的转矩误差归一化到±1之间，误差阈值δ满足：

(9)

式中:γ为期望转矩脉动系数。

模块化功率变换器单相导通区转矩误差控制原理如图5所示。控制策略如下：

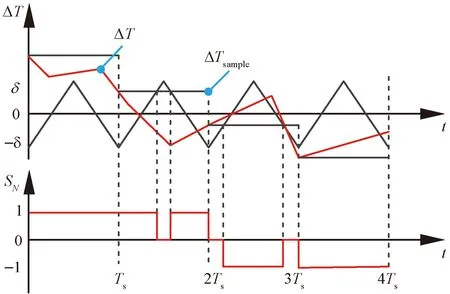
图5 模块化功率变换器单相导通转矩误差控制原理图

(10)

转矩误差控制原理如下：

1)当ΔTsample>δ时，电机参考转矩远大于实际转矩，此时电机绕组应处于“1”状态，进入快速励磁阶段，满足系统需求。

2)当0≤ΔTsample≤δ时，电机参考转矩稍大于实际转矩，此时采用PUPWM，电机绕组处于“1”和“0”状态，从而柔和地增加电机的输出转矩。

3)当-δ≤ΔTsample<0时，电机参考转矩稍小于实际转矩，此时采用NUPWM，电机绕组处于“-1”和“0”状态，从而柔和地减小电机的输出转矩。

4)当ΔTsample<-δ时，电机参考转矩远小于实际转矩，此时电机绕组应处于“-1”状态，进入快速退磁阶段，尽快减小电机输出转矩。

换相导通区转矩误差控制原理如图6所示。控制策略如下：

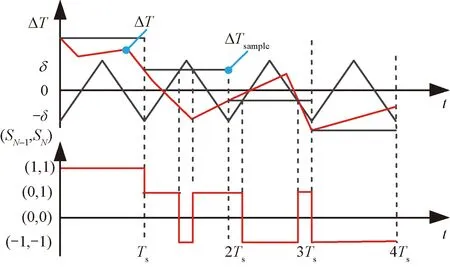
图6 模块化功率变换器换相导通转矩误差控制原理图

(11)

以B、A两相重叠导通为例，且A相为即将导通相，B相为即将关断相，转矩误差控制原理如下：

1)当ΔTsample>δ时，电机参考转矩远大于实际转矩，电机绕组应处于(1,1)状态，进入快速励磁阶段，满足系统需求。

2)当-δ≤ΔTsample≤δ时，电机参考转矩与实际转矩稍有偏差，此时A相采用BPWM调制方式，B相采用NUPWM，B、A两相电机绕组在此区间内状态可处于(1,1)，(0,1)，(0,0)，(-1,-1)4种状态，算法可根据转矩误差实际值进行快速有效调节。

3)当ΔTsample<-δ时，电机参考转矩远小于实际转矩，此时电机绕组应处于(-1,-1)状态，进入快速退磁阶段，尽快减小电机的输出转矩。

3 仿真验证

本文以一台三相12/8极SRM为样机，经过实验获取了其静态磁链特性，进而采用文献[12]神经网络非线性映射建模的方法，对曲线簇进行学习，得到完整的SRM静态特性曲线。而后根据电压平衡方程和机械方程，进行电机本体仿真模型的搭建，主要包括三相SRM模块、模块化功率变换器模块和控制器模块，如图7所示。

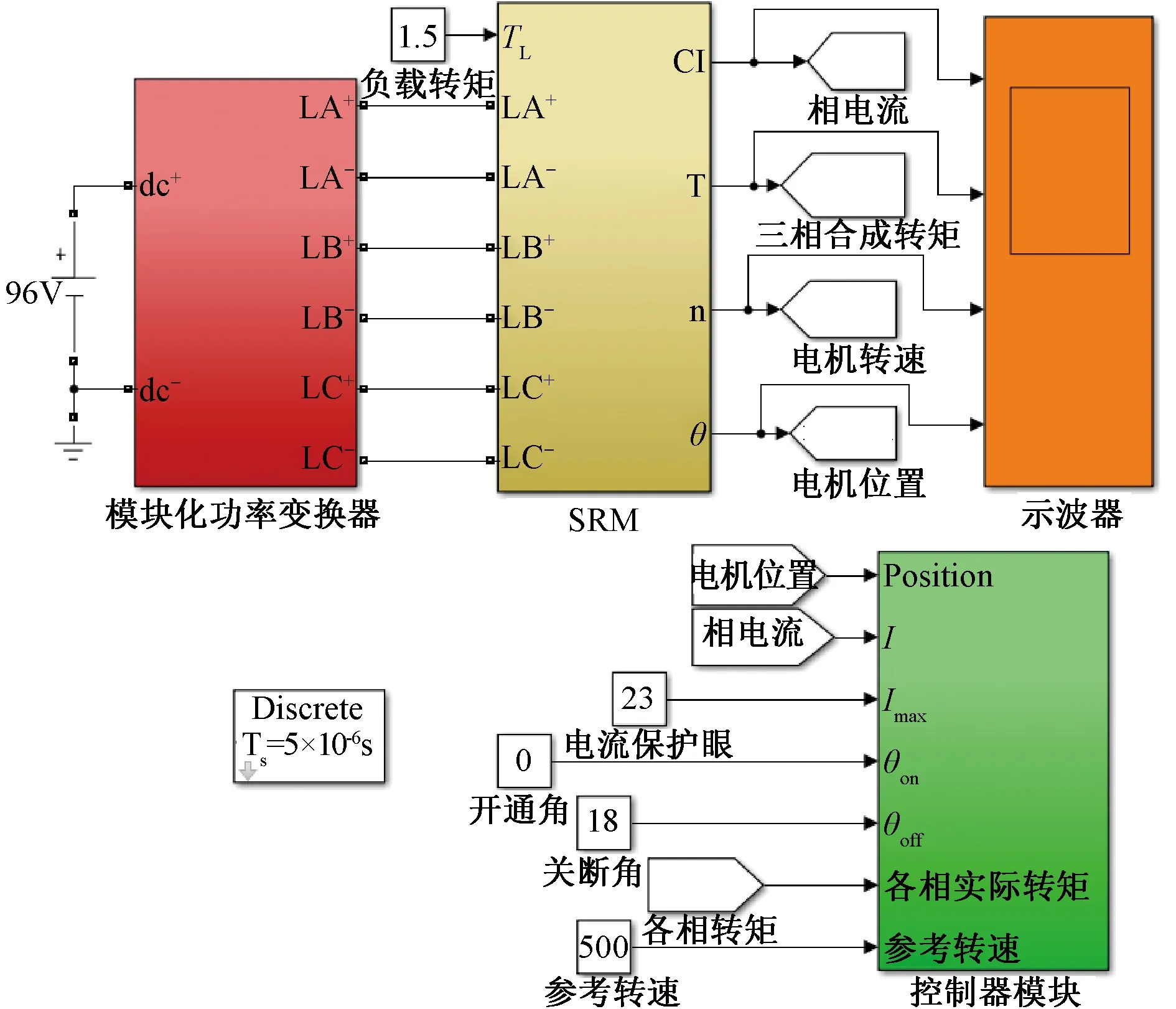
图7 模块化功率变换器驱动的SRM系统仿真模型

设定参考转速为500 r/min，采用传统DITC控制方式仿真结果如图8所示。图8中转矩脉动系数为54.39%，效率为62.85%。

图8 500 r/min时DITC仿真结果

采用改进型DITC控制方式仿真结果如图9所示。图9中转矩脉动系数下降到了31.13%，效率为63.07%。

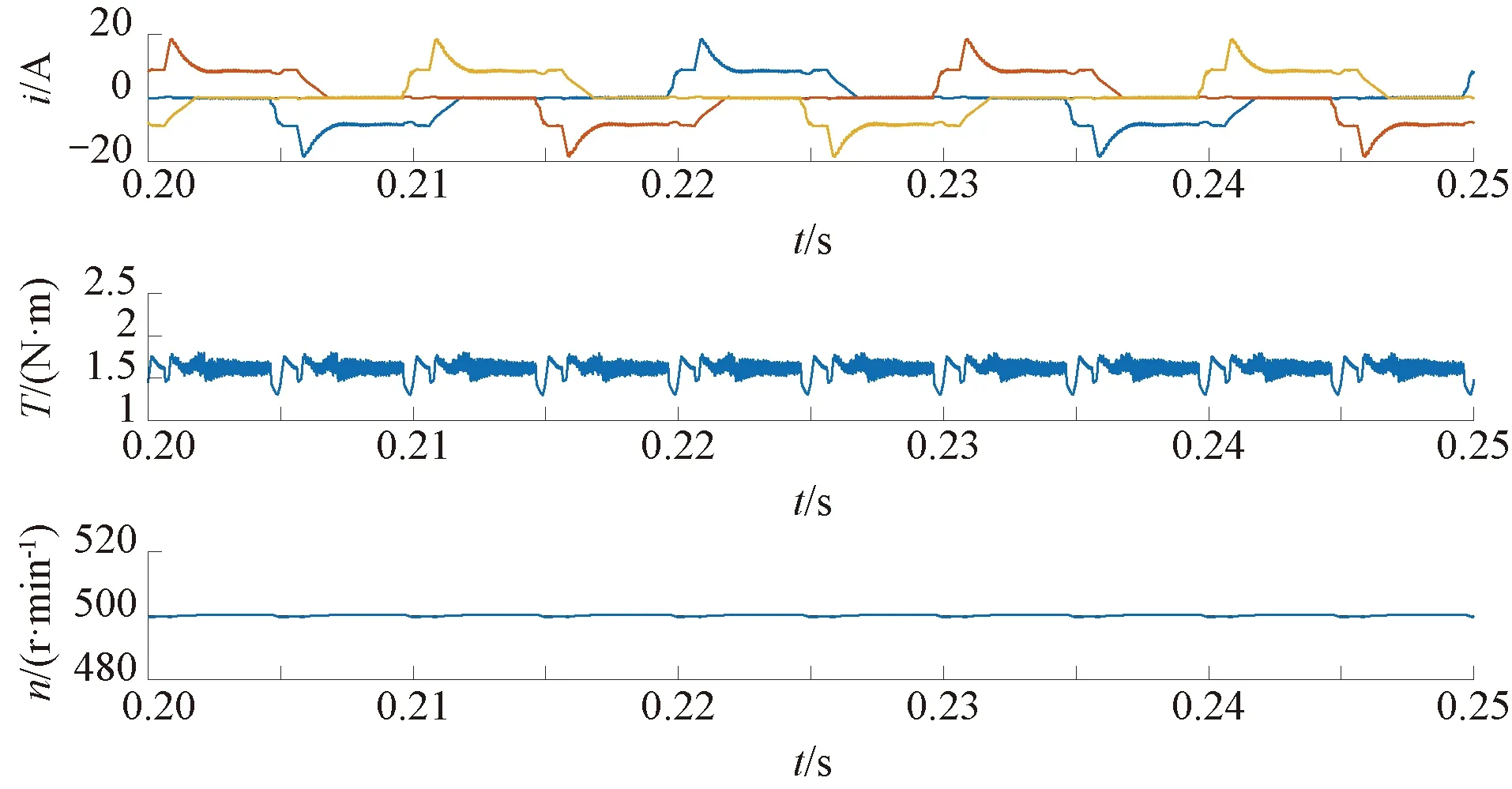
图9 500 r/min时改进型DITC仿真结果

给定参考转速为1 000 r/min，采用传统DITC控制方式仿真结果如图10所示。图10中，转矩脉动系数为65.01%，系统效率为78.85%。

图10 1 000 r/min时DITC仿真结果

采用改进型DITC控制方式仿真结果如图11所示。图11中，转矩脉动系数下降到了34.65%，系统效率为78.96%。

图11 1 000 r/min时改进型DITC仿真结果

将模块化功率变换器驱动的SRM转矩脉动的上述仿真结果进行总结，如表2所示。

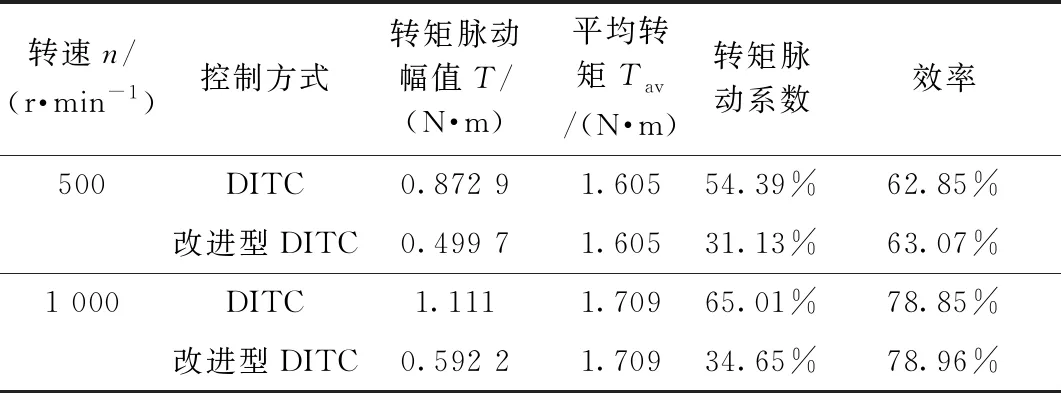
表2 SRM模块化功率变换器DITC仿真结果总结

分析表2数据可以得到如下结论：

1)电机运行在相同转速条件下，改进型DITC控制算法转矩脉动小于传统DITC控制方法，在低转速500 r/min时，改进型DITC控制方式下的，SRM转矩脉动系数可以降低到31.13%。

2)电机运行转速相同时，采用两种不同的控制算法，电机输出的平均转矩相当；对传统DITC方法改进后，不仅没有牺牲电机的输出转矩和效率，而且对转矩脉动起到较好的抑制作用，从仿真的角度证明了改进算法的有效性。

4 实验验证

目前，dSPACE在电机控制领域发挥着越来越重要的作用[13]。本文搭建的SRM驱动系统测试平台实物图如图12所示。实验中电机所加负载为1.5 N·m，分别给定不同的参考转速进行实验，实时系统中断频率为10 kHz。

图12 基于dSPACE的SRM实验平台实物照片

设定参考转速为500 r/min，采用传统DITC控制方式，实验结果如图13所示，转矩脉动系数为63.60%，系统效率为46.02%。

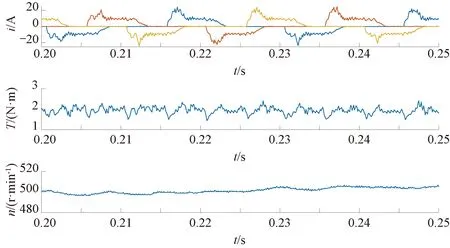
图13 500 r/min时DITC实验结果

采用改进型DITC控制方式，实验结果如图14所示。图14中转矩脉动系数下降到了38.09%，系统效率为46.38%。

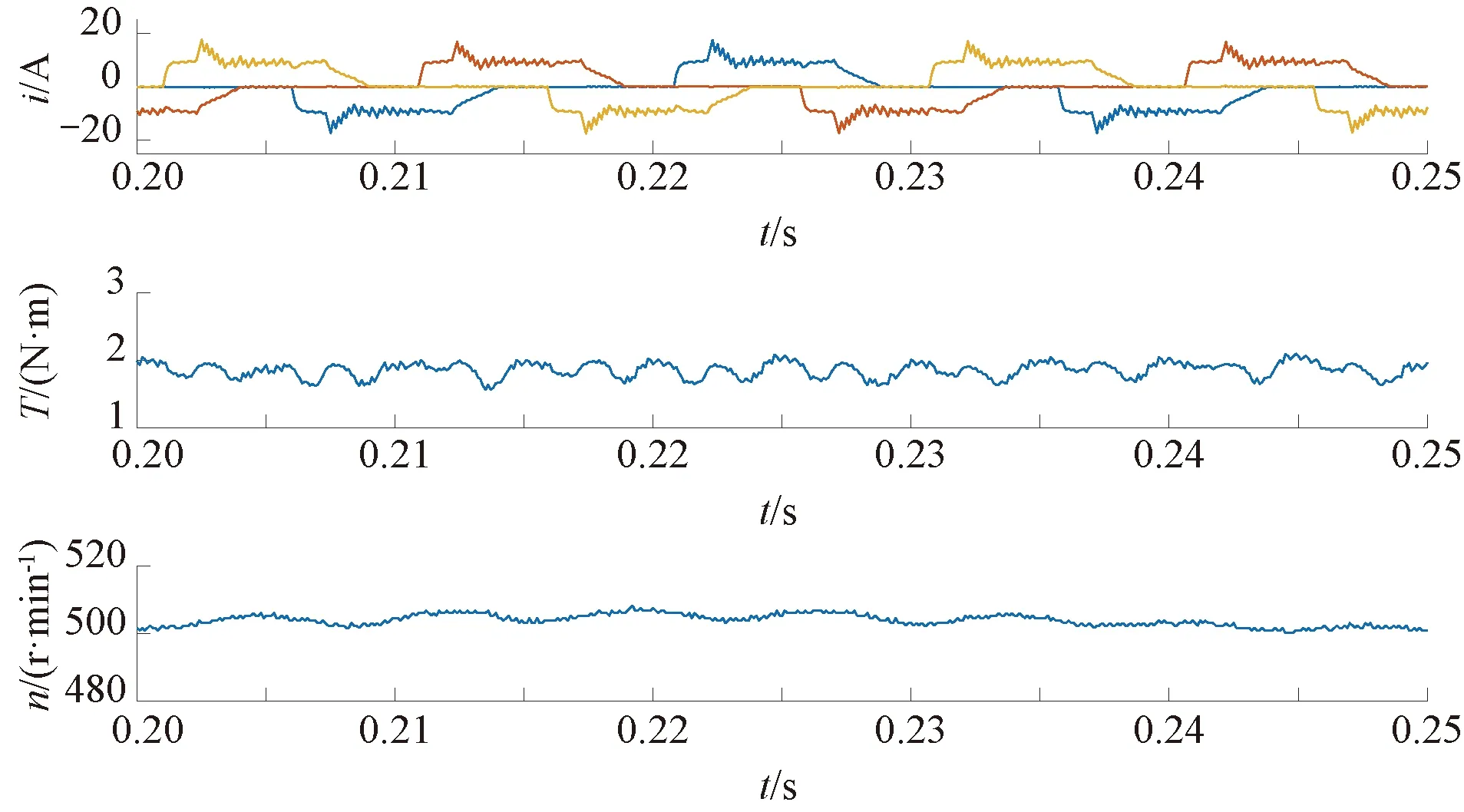
图14 500 r/min时改进型DITC实验结果

给定参考转速为1 000 r/min，采用传统DITC控制方式，实验结果如图15所示，转矩脉动系数为70.68%，系统效率为58.72%。

图15 1 000 r/min时DITC实验结果

采用改进型DITC控制方式，实验结果如图16所示。图16中，转矩脉动系数下降到了42.30%，系统效率为59.02%。

图16 1 000 r/min时改进型DITC实验结果

将模块化功率变换器驱动的SRM转矩脉动的上述实验结果进行总结，如表3所示。

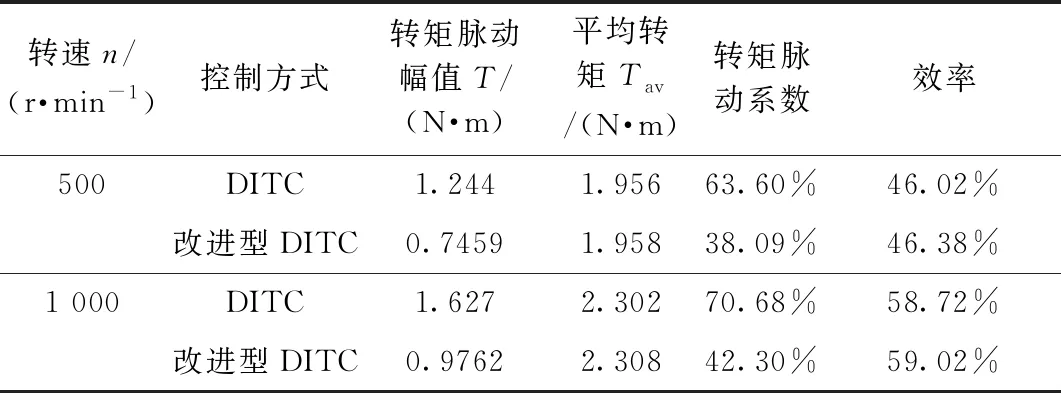
表3 SRM模块化功率变换器DITC实验结果总结

分析表3数据，可得以下结论：

1)给定相同的参考转速，本文的改进型DITC控制方法对SRM转矩脉动抑制效果要比传统DITC控制方法好。

2)相同转速条件下，从电机输出的平均转矩以及驱动系统效率看，改进的DTIC控制方法与传统DITC控制方法基本一致。

3)采用同种控制方法，随着转速的升高，SRM转矩脉动会变大，驱动系统效率会有所提升。

实验结果与仿真结果相比，转矩脉动增大，效率降低。二者之间存在差异，主要原因是仿真条件比较理想，步长设置为5×10-6s，而实验受dSPACE实时系统以及功率变换器的开关频率限制，控制系统步长为1×10-4s。

5 结 语

本文针对模块化功率变换器驱动的SRM，提出了一种基于电流重叠角优化和脉宽调制的DITC策略，实现了电流重叠角的实时计算与更新，保留了滞环控制方法快速简单的特性，并避免了其滞环带内不动作的缺点。仿真及实验结果表明，本文的改进型DITC控制方法能够有效地抑制电机的转矩波动，且不牺牲平均输出转矩和效率。