电动汽车用增程发电机的设计与优化

孙维国，胡 岩，吴家成

(沈阳工业大学 电气工程学院，沈阳 110870)

0 引 言

我国的能源消耗逐年增加，2020年我国石油消耗50%以上要依赖国外进口[1]。大力推动传统车辆的节能减排与新能源汽车的产业化，成为中国汽车工业和全球汽车工业发展趋势[2]。电动车是一种新的方案，可以降低机动车的排放量，并解决传统的能源问题，已经受到广泛的肯定[3]。永磁同步发电机是一项重要的研究课题[5]，近年来，国内外许多学者从电磁、结构等方面对其进行了深入的研究。

文献[6]利用Taguchi法优化V形永磁转子结构，通过调整每个目标函数的权重值，提出不同的最优设计结果。文献[7]提出了一种基于Taguchi法的混合设计模型，用于优化设计具有更低转矩纹波和更高效率的开关磁阻电机。文献[8]利用Taguchi法确定优化参数和取值范围，考虑了加工过程等因素对测量结果的影响，并确定了试验的正交矩阵；应用有限元软件对试验矩阵进行了求解，并对参数的变化趋势和权重进行了分析，得到了最佳参数的选取原则。上述电机优化都是采用Taguchi法，当进行多个电机性能参数优化时，该方法不能得到全局最优解。

文献[9]以等效磁路法为基础，建立了一种快速计算模型，讨论了永磁体定子内外径、轴向长度、气隙长度等参数对电动机损耗及效率的影响。文献[10]通过对不同线型绕组的交流损耗的计算，比较和分析了各种线型绕组的交直流铜损，并根据损耗的发生机制，给出了采用扁线绕组分股和换位控制交流损耗的方法。然后，根据常见的轮毂电动机运行状态，综合比较了各种线型绕组电动机的损耗及效率。上述优化方法都是通过电机计算模型或者电机等效磁路模型，该方法缺点是等效模型复杂、电机优化繁琐效率低。

文献[11]采用遗传算法实现永磁同步电动机多目标优化设计，优化永磁同步电机的效率和转矩性能，研究结果表明，基于遗传算法的优化方法具有求解速度快、优化准确等优点。文献[12]采用有限元法和Taguchi法优化电机效率，仿真实验结果表明发电机的效率与初始设计相比得到了提高。上述优化虽然都得出了优化方案，但都是针对单一或两个目标进行优化，并未涉及三个目标以上的优化。

如今，人们对电动车用发电机的效率、功率密度、振动噪声等性能要求越来越高，由于内置式永磁同步发电机的电磁转矩波动太大，会使其工作时的振动、噪声增大，损耗增大，进而影响发电机效率。此外，转矩波动太大，会使机械轴产生过度的疲劳应力，从而降低其使用寿命。因此，研究发电机的转矩波动，对提高发电机的运行效率、延长机械轴使用寿命具有十分重要的意义。

本文以一台6极36槽电动汽车用永磁同步发电机为研究对象，主要研究发电机的效率、功率密度以及转矩脉动问题。首先，通过磁路法快速计算出电机各部分尺寸，使用仿真软件建立有限元模型，采用有限元方法对初步设计方案进行验证。其次，通过参数化建模初步找出对发电机性能参数影响较大的9个设计参数作为优化因子，采用基于Taguchi法的参数敏感度分析，从9个设计参数中筛选出影响权重大于20%的参数，采用CCD(中心复合设计)试验样本点选取技术进行采样，拟合出各性能参数与不同优化因子的响应面，通过遗传算法进行全局寻优，得出最优解，对影响权重小于20%的参数，考虑参数之间相关与否，对相关联的参数进行基于响应面法参数优化，对不相关联的参数使用参数化扫描法进行优化。最后，利用有限元分析软件对其进行分析。结果表明，本文的优化方法能够有效减少电机优化时间，为增程发电机的设计优化提供了一定的指导和参考意义。

1 电机初始参数的设计及有限元分析

目前，利用有限元仿真软件对所有电机都可以进行设计和操作模拟。有限元方法已经发展到了较为成熟、可靠的地步，它能够实现整个系统的参数设计和调试，以及各种运行状态的仿真。本文从发电机的主要设计指标出发，结合设计经验和计算公式，得出了发电机的关键参数，如表1所示。建立二维有限元模型，如图1所示。

图1 电机有限元模型

表1 电机关键参数

利用有限元分析软件绘制电机的1/6模型，利用有限元方法对电机的初始设计进行验证，并给出空载磁密分布云图，如图2所示。

图2 空载磁密分布云图

由图2可知，最大磁通密度是在永磁体隔磁桥与转子外边界之间产生，最大值为2.183 7 T，磁通密度饱和可防止磁力线在永磁体两侧形成闭合回路产生漏磁，定子齿、定子轭、转子轭的磁通密度在1.2～1.5 T之间，满足电机设计磁负荷要求，因此铁磁材料选择合理，电机初步方案设计较为合理。

2 电机优化流程

本次优化涉及到的优化因子众多，而且不同优化因子对性能参数的影响权重和彼此之间相关性不同，同时还需考虑优化时间的限制和准确度的要求。为此，本文针对不同的结构参数对优化目标的影响，采用了相应的优化设计方法。增程发电机的优化设计流程如图3所示。

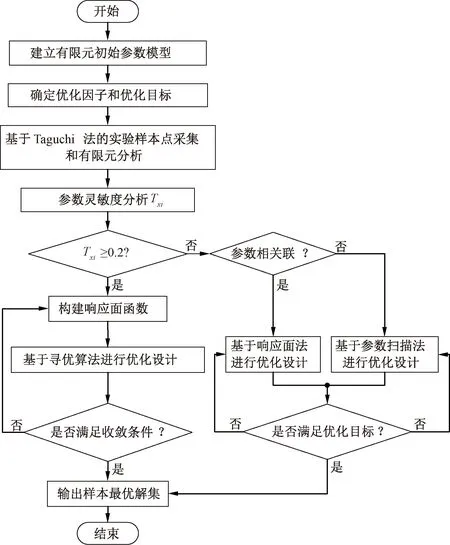
图3 优化方法流程图

2.1 优化目标和优化因子的选取

为满足内置式增程发电机高效稳定的运行需求，本文选取磁化方向长度hm、永磁体长度hl、定子外径Dd、转子外径DZ、极弧系数αp和定转子铁心长度L、隔磁磁桥长度lbridge、倒角宽度ωrib和定子斜槽qskew为优化因子，取值范围如表2所示，以降低电磁转矩波动、提高电机功率密度和效率为优化目标。目标函数为转矩脉动最小，功率密度和效率最大。此时，增程发电机设计的多目标优化函数y(xi)可以定义为数学函数表达式：

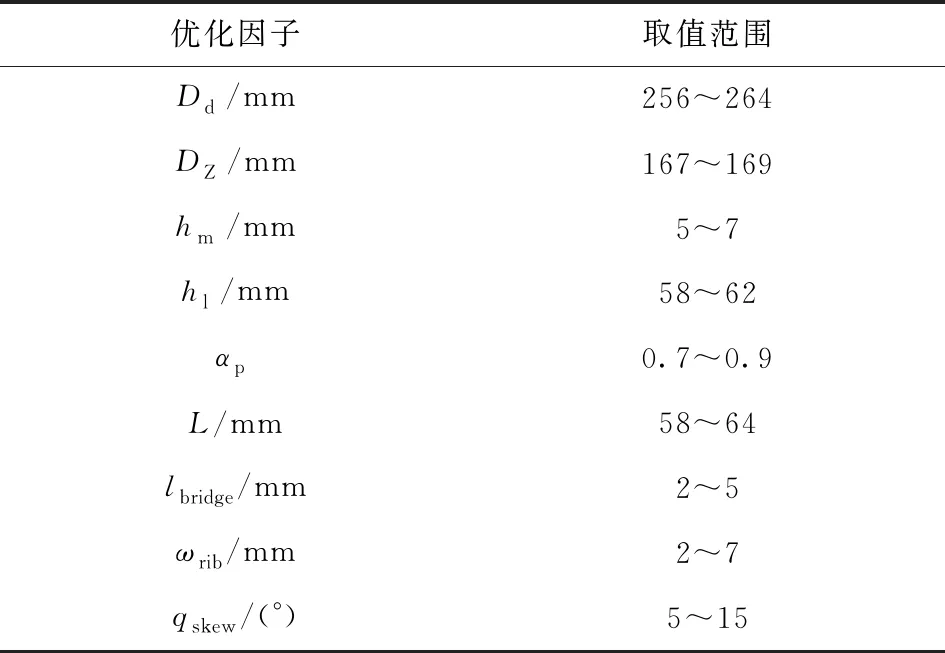
表2 优化因子取值范围

(1)

λ1+λ2+λ3=1

(2)

xi=(Dd,DZ,hm,hl,αp,L,lbridge,ωrib,qskew)

(3)

式中:xi为电机设计参数；ΔT为转矩脉动；η为效率；ρm为功率密度；yη(xi)、yρm(xi)和yΔT(xi)分别表示当xi取某一值时电机效率、功率密度和转矩脉动的大小；λ1、λ2和λ3分别为电机效率、功率密度和转矩脉动对应的权重。考虑到本文设计的电机对发电效率要求较高，权重系数λ1取为0.5，而λ2和λ3取值为0.25。优化目标要求转矩脉动最小，因此转矩脉动函数放在分母上，当多目标优化函数y(xi)取最大值时yη(xi)和yρm(xi)的值就会最大，yΔT(xi)的值就会最小。

在仿真实验时，电机的机械损耗无法通过仿真得到，因此根据经验将机械损耗按输入功率的1%计算，得到发电机效率计算公式：

(4)

式中：P1为发电机的输入功率；pFe为定转子铁耗；pcua为定子绕组铜耗；padd为电机附加损耗；psl为永磁体涡流损耗。

发电机电磁转矩波动计算公式：

(5)

式中:Te max、Te min、Te avg分别为最大转矩、最小转矩和平均转矩。

功率密度计算公式：

(6)

式中:P2为发电机输出功率；M为电机有效质量。

2.2 参数灵敏度分析

通过灵敏度分析确定每个变量对电机性能的影响权重。对于9因素3水平的试验，一共需要做39次仿真分析，本文利用正交试验只需做27次仿真即可。通过仿真软件进行响应面建立和优化因子参数化，整个优化过程在保证优化效率和准确度的前提下，大大缩短了仿真时间。优化因子水平值和正交表分别如表3、表4所示。

表3 优化因子水平值

表4 正交表

1)通过仿真分析计算出发电机效率、电磁转矩脉动和功率密度27组数据的平均值，公式如式(7)所示。

2)由于发电机性能在每个影响因子不同水平因素下的表现存在差异，为了更好地评估每个参数对电机不同性能的影响，需要进一步计算不同水平值下的实验结果均值。

3)通过方差计算出影响因子对各性能参数的影响比重如式(8)所示。最后通过式(9)计算出各优化因子所占总比重。

(7)

(8)

Txi=λ1Axi+λ2Bxi+λ3Cxi

(9)

对电网调度工作监管的不到位和流于形式是导致工作中出现失误的一个重要原因，主要体现在审票的不严格和操作监督的不到位上。这样的一些监管上的不到位，使得工作中的失误不能够被及时发现，使得误操作的发生频率大大提高。

选取对优化目标影响大的优化变量，定义影响权重大于20%的优化因子为重要因素，通过寻优算法进行全局寻优得到最优解。将影响权重小于20%的优化因子定义为次要因素，并根据参数相关性大小分为相关因子和不相关因子，相关因子通过响应面法确定最优解，不相关因子通过参数扫描法确定最优解。影响权重分析结果如表5所示。

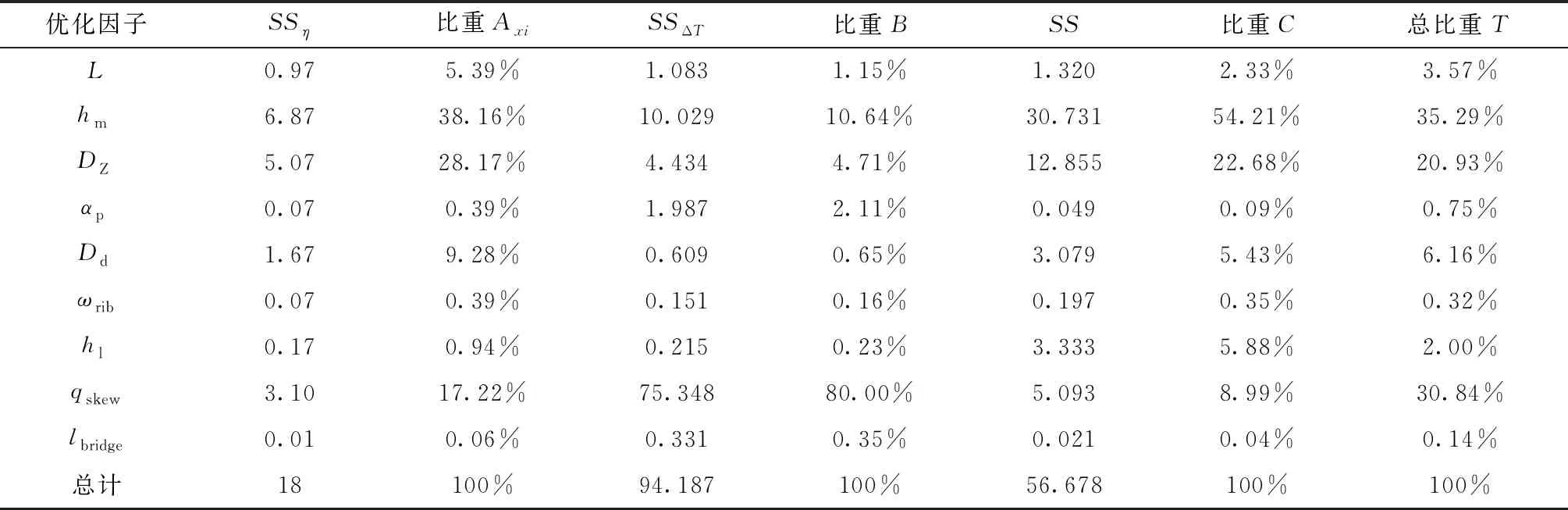
表5 优化因子影响比重

2.3 参数优化

根据各影响因子所占总比重的大小将Txi大于20%的参数hm、DZ、qskew定义为强敏感因子，他们之间相互作用性强，会产生交叉影响，因此通过寻优算法找到最优解，将Txi小于20%的影响因子L、αp、Dd、ωrib、hl、lbridge定义为弱敏感因子，其中L和Dd与电机的体积、成本和形状有关，ωrib和hl对磁力线走向有关，因此将他们定义为相关参数，将αp和lbridge定义为不相关参数。

遗传算法是基于自然选择和遗传原理，将优胜劣汰原则与种群内染色体间的随机信息交换机制相结合的一种有效的全局搜索方法。设置种群大小为150，最大迭代次数设置为50，样本点取1 500个，目标函数为y(xi)，通过交叉、变异操作，对群体的遗传基因进行了连续的更新，图4为目标函数y(xi)的迭代收敛情况。可以看出，经过变量的全局寻优，在样本点达到1 100个左右时，函数y(xi)值达到最大，约为125。

响应面模型通过有限元软件计算出多个设计变量的样本点，将有限元计算的各点用函数的形式进行拟合，从而最大限度地减小了试验和建立的响应面之间的误差，提高拟合精度。在此基础上，对电动机的效率、转矩、功率密度进行响应面拟合。根据响应面模型和色彩分布，确定了各参数的最优范围。

响应面的二阶回归模型表示：

(10)

式中：y是响应变量；β是回归系数；x表示不同的优化变量。

结合图5可以看出，功率密度和发电机效率与定转子铁心长度成正相关，但增加的幅度递减；相反，转矩波动与铁心长度成负相关。还可看出，随着定子外径的增加，功率密度逐渐减小，发电机效率逐渐提高而转矩脉动则是先增加后减小。同理，根据各性能参数与隔磁桥倒角宽度和永磁体长度拟合出的响应面显示，电机效率、功率密度和转矩脉动都随着hl和ωrib的增加，先增加后减小。综合上述分析，最终确定该电机的关键结构尺寸L为64 mm，Dd为261.6 mm，ωrib为7 mm，hl为61.8 mm。这样既能保证发电机具有较高的电机效率和功率密度，又能降低电机的转矩脉动。

图5 响应面结果图

利用参数扫描法对发电机极弧系数和永磁体倒角度进行优化，多目标优化函数y(xi)随极弧系数和隔磁磁桥长度宽度变化的关系曲线如图6和图7所示。

图6 目标函数随磁桥长度变化图

图7 目标函数随极弧系数变化图

由图6、图7可知，当lbridge取2 mm、αp取0.85时，目标函数取得最大值。综合上述分析，最终确定了该电机的关键结构尺寸，如表6所示。

表6 优化前后尺寸对比

3 有限元模型分析与验证

为验证本文的基于优化因子影响权重与多目标优化方法相结合方法的可靠性，利用有限元软件对发电机进行二维建模，并对电磁性能进行全面的分析。优化前后性能参数对比如表7所示，可以看出，电机效率相比于优化前提升了0.35%；转矩脉动优化更加明显，降低了32.64%；功率密度也由1.93 W/kg增加到2.09 W/kg。综上所述，可以看出优化后发电机效率和功率密度提高了，同时转矩波动减小了，计算时间缩短了，发电机的性能提高了。

表7 电机优化前后性能对比

在空载工况下进行有限元分析，转子额定转速为 6 000 r/min，得到发电机优化前后A相空载反电动势波形如图8所示。从图8中可以观察到空载反电动势谐波成分显著减少，波形更加趋于正弦波。设置定子斜槽角为7.5°，分段数为3，步长为0.2°，得到一个周期齿槽转矩波形，如图9所示。可以看出，齿槽转矩显著降低，峰值由原来的2.266 N·m降低到0.349 N·m，发电机运行更加平稳，噪声更小。气隙磁密柱状对比图如图10所示，由图10可知，除了3次和15次谐波外，其它各次谐波均有所减小，对发电机的转矩波动起到了较好的抑制作用。从图11可以看出，经过多目标优化后，发电机稳定运行时电磁转矩波形变得更加平滑，上下波动幅度更小。

图8 A相空载反电动势波形图

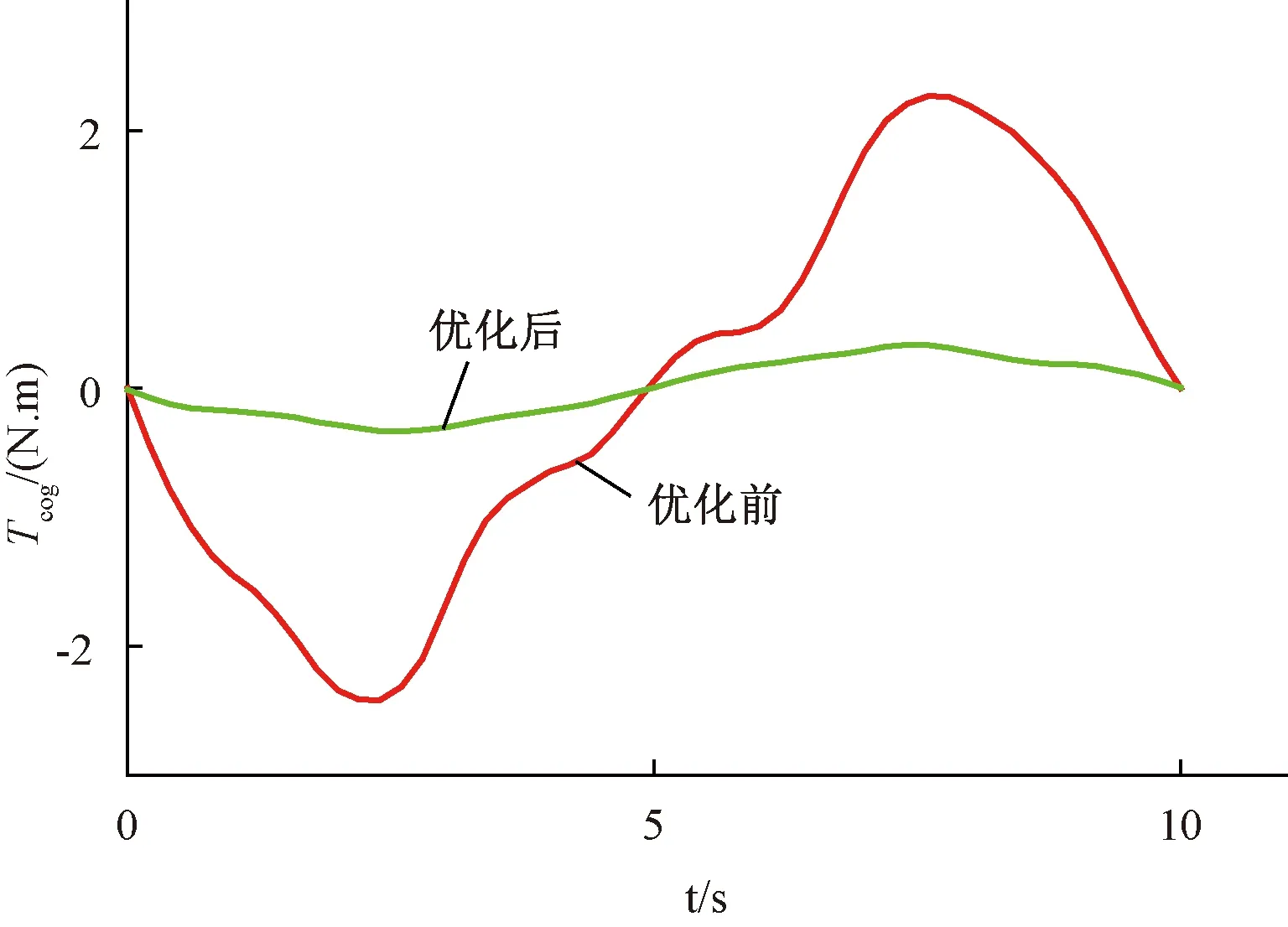
图9 齿槽转矩波形图

图10 气隙磁密幅值分布图

图11 电磁转矩波形图

4 结 语

本文根据优化因子对性能指标影响权重大小、以及优化因子之间的相关性，将优化因子进行分类并采用遗传算法、响应面法、参数扫描法相结合的方法对电机关键结构尺寸进行全面优化，快速有效地优化出满足电机性能的结构参数，利用有限元软件，对优化前后的发电机进行了性能对比分析。可以得出：

1)采用遗传算法、响应面法和参数扫描法相结合的方法对电机关键结构尺寸进行全面优化，相较于只采用某一种方法对电机进行多目标优化，该方法更有针对性，重要因素和次要因素都得到优化。

2)永磁体磁化方向长度hm、转子外径DZ和定子斜槽qskew对增程发电机效率、转矩脉动、功率密度有重要影响。通过多目标优化效率提高了0.35%，功率密度提高了8.29%，电磁转矩脉动降低了32.64%。电机性能得到明显改善，发电机在运转过程中的振动和噪声降低了，发电机的损耗降低了。另外，机械轴的疲劳应力也变小，增加了轴的寿命，降低了电机维护的成本。

3)通过对电机关键参数的优化，空载反电动势波形畸变率由原来13.86%降低到9.39%，谐波含量减小，波形更趋近于正弦波，发电机输出电压质量更高；齿槽转矩得到明显削弱，数值趋近于零，电机的振动噪声减小了，电机运行更加平稳；5次、7次、9次、11次和13次气隙磁密谐波均有明显降低。