混合式步进电机自定位转矩的二维有限元仿真设计研究

陈薇薇，郭默佳，张洪岩

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引 言

混合式步进电机控制简单、可靠性高、响应速度快，且能在断电情况下提供一定的保持转矩，即自定位转矩的优点，因此被广泛应用于航空航天、卫星探测等众多领域。某航天器载荷转移机构中需要采用一种具有一定自定位转矩的混合式步进电机，并且要求该转矩大小在一个特定的范围内，既能保证在断电情况下可以维持电机不转动，也可在稍加电流后便可克服自定位转矩将电机起动。混合式步进电机的磁场呈三维分布，即径向磁场和轴向磁场并存[1]，气隙及相邻齿槽处的磁场变化复杂且剧烈，从而使电机特性呈非线性，利用传统的齿层比磁导方法计算误差较大。三维有限元分析计算方法较为精确，可以实现径向、轴向磁路的耦合，但由于气隙和齿槽尺寸小，对网格剖分的要求很高，故对计算机的硬件条件提出了高要求[2]。

文献[3]分析了一种轴向分相混合式永磁步进电机，如图1所示，提出了采用磁路计算法计算轴向分相步进电机的自定位转矩，在磁路不饱和的情况下，可采用调整转子铁心长度的方法来改变其自定位转矩的大小，该方法简便有效且可操作性强，但存在较大的局限性，不适用于所有类型的混合式步进电机，且在磁路较为饱和的情况下同样不适用，因此方法通用性不高。

图1 轴向分相混合式永磁步进电动机

文献[4]提出了一种用以替代3D有限元仿真计算的代数方程算法，该方法通过一些假设来预置磁路，得到等效磁路模型，依此计算气隙磁导，最后得到电机的电磁参数，计算得到电机的自定位转矩。该文对两相电机进行分析和验证，其结果同样适用于n相电机的自定位转矩计算。这种方法能得到较为准确的自定位转矩峰值，但不适用于磁路饱和的电机，且无法查看磁路分布情况。

针对航天任务特殊的应用需求，本文提出了一种可较为精确计算混合式步进电机自定位转矩的方法，即平铺展开定转子，将三维电机模型等效为二维模型。首先从磁路分析的角度论证其原理可行性，然后对电机模型进行等效变换，并给出变换过程，建立了有限元模型进行仿真计算，最后试制了样机进行试验验证。

1 电机等效变换模型

本文混合式步进电机的主要电磁结构如图2所示，主要组成部分包括定子铁心、永磁体和两段转子铁心，自定位转矩与绕组无关，因此将定子绕组忽略，同时忽略机壳、端盖、转轴等对磁路基本无影响的零部件。

图2 混合式步进电机主要结构图

将三维电机模型等效变换成二维模型，需要基于以下假设条件：

1)等效后定子磁路部分的磁路长度与等效前基本一致，因此定子磁路的磁阻只和磁路的有效横截面积有关；

2)等效后的电机内部永磁体提供的磁通以及磁动势和等效前基本一致。

在以上两个条件下，等效模型中的齿层尺寸和气隙尺寸均保持不变，其余模型参数利用磁通不变的原则进行等效变换后，可以认为等效后模型的静态特性包括自定位转矩与原电机的基本相似。

等效变换后的模型示意图如图3所示。

图3 等效变换后的模型示意图

等效变换前电机转子为两段环形铁心，转子铁心I和转子铁心II相互错开半个齿距，等效变换后，等效转子铁心I和等效转子铁心II上下相对且左右偏移半个齿距；环形定子铁心共有8个大极，分割成为上下平行的两段等效定子铁心，分别有4个大极，即等效定子铁心I和等效定子铁心II；一片环形永磁体均分为4块长方形等效永磁体。利用磁路中磁通不变原理，定转子小齿槽尺寸不变，永磁体厚度也不变，定子铁心长、转子铁心长需做平铺拉伸处理，同时，定子轭部高、定子大极宽、转子轭部高也需要进行等效计算。

在处理定子铁心时，以转子铁心长度和外径作为基准，可认为等效模型的厚度就是一段转子铁心的长度Lra，同时得到等效定子铁心长Ls_DX为：

(1)

式中：Dro为转子铁心外径。

定子轭部和大极在等效变换过程中，利用变换前后体积中磁通量相同的原则，等效定子轭部高度hcs_DX可以表示为：

(2)

式中：Lra为每段转子铁心长；Lm为永磁体厚度；hcs为定子铁心轭部高；Dso为定子铁心外径。

等效定子大极宽bp_DX可以表示为：

(3)

式中：bp为定子大极宽。

转子的等效变换采用同样的原理，等效转子铁心长Lr_DX可表示为：

(4)

式中：Zr为转子齿数。

等效转子轭部高hcr_DX可表示为：

(5)

式中：Lj12为转子挖空厚度；Dj2为转子挖空内径；Dri为转子内径；hrt为转子小齿高；α为挖空倾斜角；Dmo为永磁体外径；Dmi为永磁体内径。

永磁体每块长度Lm1_DX可表示为：

(6)

式中：Zs为定子大极数。

2 仿真计算

根据前文提出的模型变换方法，对某航天机构用混合式步进电机进行参数等效变换，原模型和等效变换后的电机参数如表1和表2所示。

表1 电机主要设计参数

表2 等效变换后的电机主要设计参数

等效定子铁心I的4个大极和等效转子铁心I分别相互错0、1/4、1/2、3/4小齿，等效定子铁心II的4个大极和等效转子铁心II分别相互错1/2、3/4、0、1/4小齿，图4是等效变换后的电机二维仿真模型。

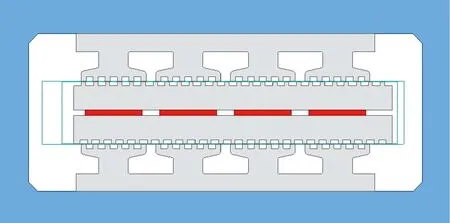
图4 电机二维仿真模型图

图5是二维求解域模型的网格剖分图，齿层部位磁路对电机性能的影响远大于轭部磁路，因此对齿层部分的网格进行加密处理，以得到更为准确的仿真结果。

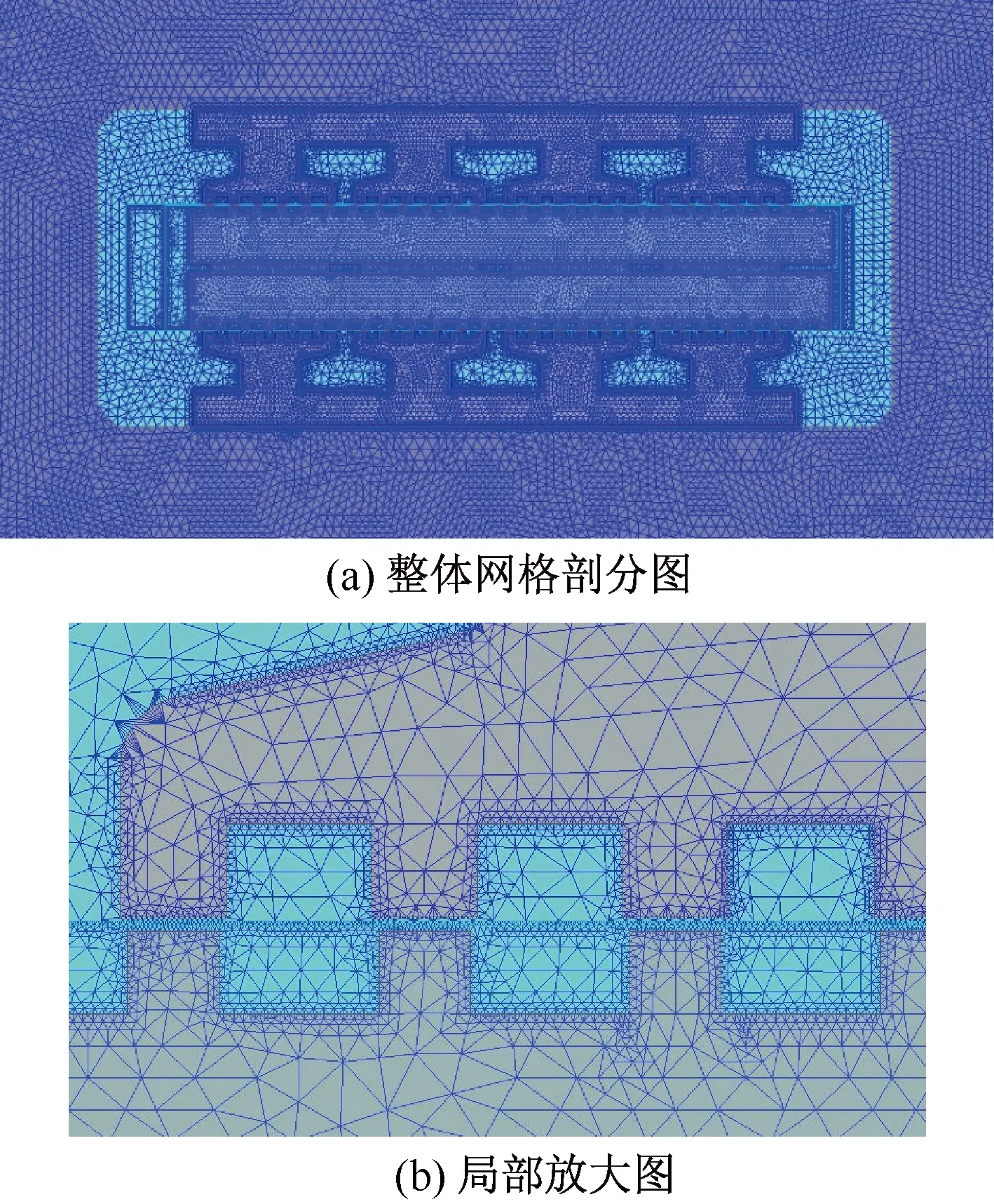
图5 网格剖分图

从图6磁力线分布图可以看出，整个模型周期中，磁密是非均匀分布的，齿与齿相对以及齿与槽相对的位置磁密最高。

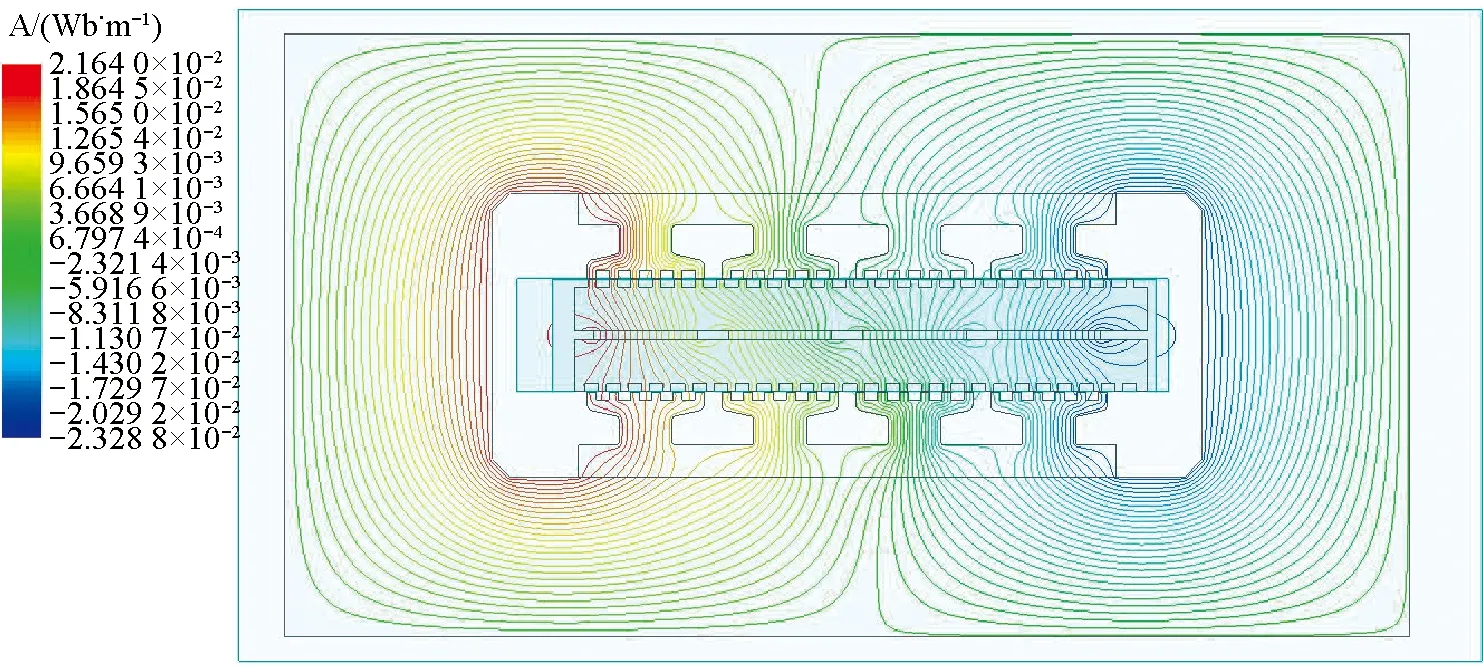
图6 电机磁力线分布图

由图7磁场分布云图可直观看出，电机磁场没有明显饱和的部位，磁密相对较高的部位是定、转子小齿以及极靴处，该齿槽结构比较合理。两种步距角，不同气隙下自定位转矩峰值的仿真结果如图8所示。可见，1.8°步距角电机的自定位转矩明显大于0.9°步距角电机。随着气隙增大，自定位转矩呈减小的趋势，且为非线性变化，在气隙较小时，随着气隙增加，自定位转矩下降更快，气隙增大到一定程度时，气隙的变化对自定位转矩的影响开始减小。因此，若需要减小自定位转矩，可采用在一定范围内增加气隙的方法来实现(这里不考虑对电机其他性能的影响，只分析自定位转矩)。

图7 电机磁场分布云图

图8 自定位转矩-气隙仿真曲线

图9给出的是0.9°步距角，气隙0.2 mm电机模型的自定位转矩仿真结果，曲线呈规律的正弦周期性变化，自定位转矩周期是1/4齿距角[5]。

图9 自定位转矩仿真结果(0.9°步距角,气隙0.2 mm)

3 试验测试

根据上述分析与设计，研制了两台混合式步进电机样机，如图10所示，样机1为1.8°步距角，样机2为0.9°步距角。样机为分装式结构，定、转子通过一对深沟球轴承将试验机壳、试验端盖和试验转轴装配起来，保证气隙均匀度。

本文采用改变气隙的方法来验证仿真结果，可通过磨转子外圆得到不同转子外径尺寸，从而得到不同气隙，相比于改变电机齿宽齿距比，该方法可在样机上直接多次操作，简单且经济。

测试时，将电机安装在试验支架上，电机断电，用手动挂砝码的方法测试电机在不同气隙下的自定位转矩，原则是测试多次取最小值，试验结果见表3。

图11是两台样机的仿真值和实测值的对比曲线。从图11可以看到实测值和仿真值的一致性较

图11 两台样机的自定位转矩-气隙曲线

好，实测值基本上略大于仿真值，这是由于试验轴承装配时有一定的摩擦力，测得的自定位转矩中包含了一小部分的摩擦转矩，而仿真中是忽略此项的，加上自定位转矩值本身比较小，试验过程中手动加砝码存在误差，另外仿真计算也存在误差。但仿真与实测值一致性较好，所以可以认为样机的试验结果与基于二维等效变换的仿真分析结果是吻合的。

4 结 语

本文以磁通不变为原则，对电机模型进行等效变换，提出了一种二维等效有限元模型，给出了计算方法，并对不同步距角、不同气隙的结构形式进行仿真、比较，得到不同的自定位转矩方案。经过两台步距角分别为0.9°和1.8°的混合式步进电机样机的测试，进一步验证了这种基于模型等效变换的仿真分析方法的可行性和准确性，为精确计算电机自定位转矩提供了新的思路。