基于KDE及Markov的高速列车传动系振动评价及可靠性分析

刘玉梅 ，陈 云 ,2，赵聪聪 ，熊明烨

（1.吉林大学交通学院，吉林 长春 130022；2.北华大学土木与交通学院，吉林 吉林 132013；3.吉林农业大学工程技术学院，吉林 长春 130118；4.伊利诺伊大学厄巴那-香槟分校电子与计算机学院，伊利诺伊 香槟 IL61801）

高速列车传动系统作为高速列车动力传递的关键系统，其振动状况对传动系的使用寿命、整车的行驶平顺性及乘坐舒适性有重要影响，其可靠性影响整车运行的可靠性及乘坐安全性，因此对传动系关键部件的振动状态进行评价以及传动系可靠性的分析很有必要[1].

振动评价一般通过基于振动速度数据得到的振动烈度进行评价[2].目前，振动速度数据主要通过振动加速度积分获得，在信号处理和积分过程中会产生一定的误差.通用机械领域的评价标准并不适用高速列车传动系的振动评价[3]，采用振动加速度能够很好地反映振动冲击力的大小，并且在频谱分析时，可以反映振动能量随频率的变化情况，故通过采集高速列车传动系关键部件的振动加速度数据对系统进行振动评价及可靠性分析.核密度估计方法是进行分布密度函数估计的有效方法，在工程领域应用也比较广泛[4].以实际采集的样本数据为基础，不附加任何假设条件，使得分布密度函数的估计更加符合实际，基于传动系的振动数据得到的振动参考阈值具有实际参考价值.文中将运行路线上实车采集的振动加速度数据作为样本数据，通过核密度估计方法对传动系的振动数据进行分析，并据此进行振动评价.

通过机械系统的可靠性分析可以得出影响系统可靠性的主、次因素，进而采取相应的改进手段来提高系统可靠性.目前，机械系统的可靠性分析常用方法有：基于应力-强度干涉模型的零件及系统可靠性分析、基于故障树分析的系统可靠性分析、基于蒙特卡洛方法的可靠性分析、基于故障率模型的可靠性分析、基于Markov过程的可靠性动态分析方法等[5].Markov统计模型在预测系统未来状态时，不考虑其他历史状态，仅基于系统紧邻的前一种状态推算转移概率，通过初始状态概率向量及转移概率矩阵推测推测系统的稳态可用性.本文将高速列车的传动系统及关键部件划分“故障”和“安全”两种状态，建立Markov模型，依据系统的故障机制模型推测系统实时失效率，分析系统的可靠性，另外，依据分析结果可对系统检修周期的优化提供参考.

1 核密度估计理论及Markov模型

1.1 KDE理论

核密度估计（KDE）是基于样本本身性质估计样本分布的概率密度函数[6].用f(x) 和F(x) 分别表示随机变量X的概率密度函数和分布函数.从总体中随机抽取n个独立同分布样本X1,X2,···,Xi,···,Xn，样本值为x1,x2,···,xi,···,xn，则在点x处分布密度函数的核密度估计为

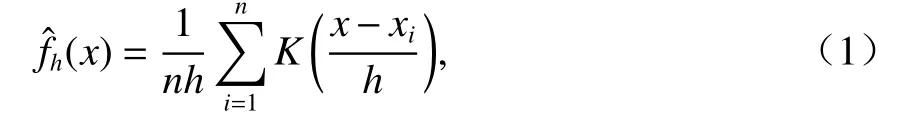
式中：K(·) 为选取的概率密度核函数；h为窗宽，h的选择直接影响核密度估计曲线的质量[7]，如式（2）.

式中： σˆ 为样本的标准差.

因此，概率分布函数的核密度估计为

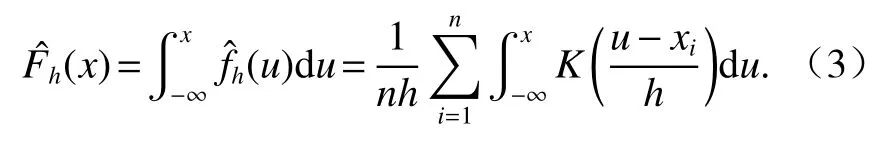
核密度估计常采用的核函数为高斯核函数和伽马核函数[8]，为了便于数学性质表达，通常采用高斯核函数[9]，即

当选定高斯内核进行核密度估计时，概率分布函数的核密度估计为

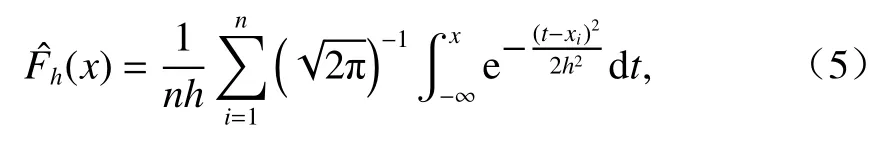
式中：t为时间.

若给定显著性水平为 α ，则置信度为 1 -α 的置信区间为

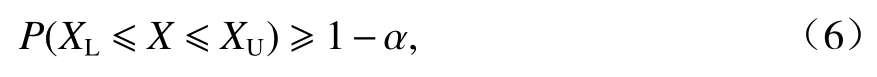
式中：XL、XU分别为置信区间下限和置信区间上限.

置信区间在进行估计时，在满足置信度要求的前提下，最优置信区间估计即为区间长度最短的置信区间.

1.2 Markov模型理论

假设随机过程X(t) 在时间集合 {t1,t2,···,tn} 上对应状态为 [x1x2···xn]，其中 0 ≤t1＜ ···＜tn，若式 (7)成立，则称 {X(t);t≥0} 为Markov过程.

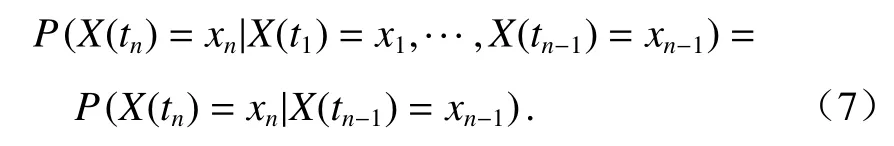
式(7)说明预测系统将来的状态X(t) 只与系统当前的状态X(tn-1) 有关，与过去其他的历史状态无关，该性质即Markov过程的“无记忆性”.此性质大大简化了推理过程，并且经过实践验证，预测结果可靠.

如果Markov过程X(t) 是离散型随机变量，则该过程又称为Markov链，设其有限空间状态为

在求解X(t) 处于某一状态k的概率Pk(t) 时，需要确定该Markov过程从一个状态j到另一个状态k的状态间转移概率，即

2 高速列车传动系振动评价

2.1 振动数据的采集

在进行实车采集传动系振动加速度信号时，需要将传感器布置在合理的测点位置.传动系的关键部件包括电机轴承，轴箱轴承，齿轮箱箱体，大、小齿轮，C型支架[10].振动加速度传感器在各关键部件的测点布置如图1所示.

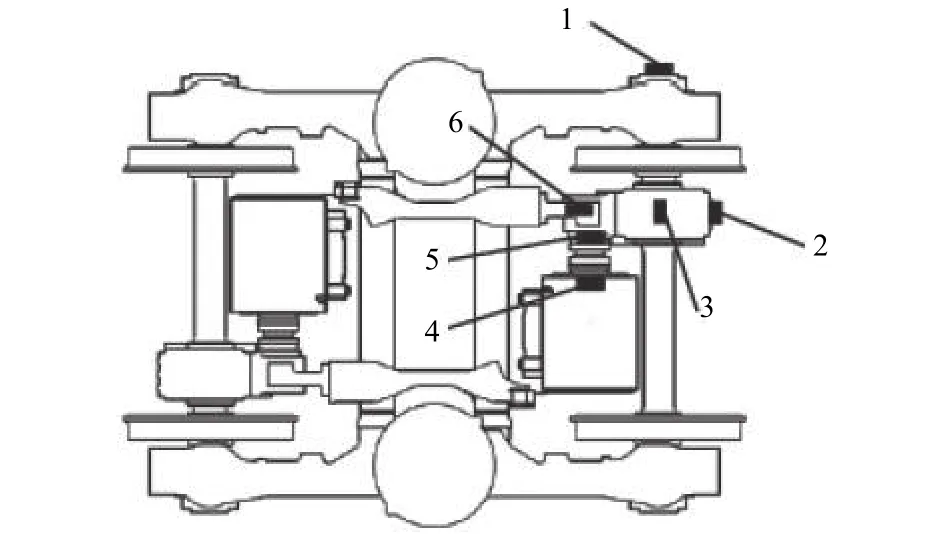
图1 加速度传感器的测点布置Fig.1 Measuring point arrangement of acceleration sensor

高速列车沿线运行时，数据采集系统将各个测点的纵向、垂向及横向的振动加速度数值进行实时存储.该型高速列车的行车速度等级为300 km/h，采用LMS系统进行数据采集，采样频率为2 048 Hz.

2.2 传动系关键部件振动的核密度估计

在进行信号采集的过程中，轴箱轴承和电机轴承取纵向（Y）和垂向（z）27′ 的振动加速度数据，齿轮箱端部、大齿轮上方、小齿轮上方及C型支架上的4个测点测取横向（X）、纵向（Y）及垂向（Z）的振动加速度数据.

在MATLAB中对采集的样本进行核密度估计，核密度估计过程中对各组样本数据选择的窗宽如表1所示.

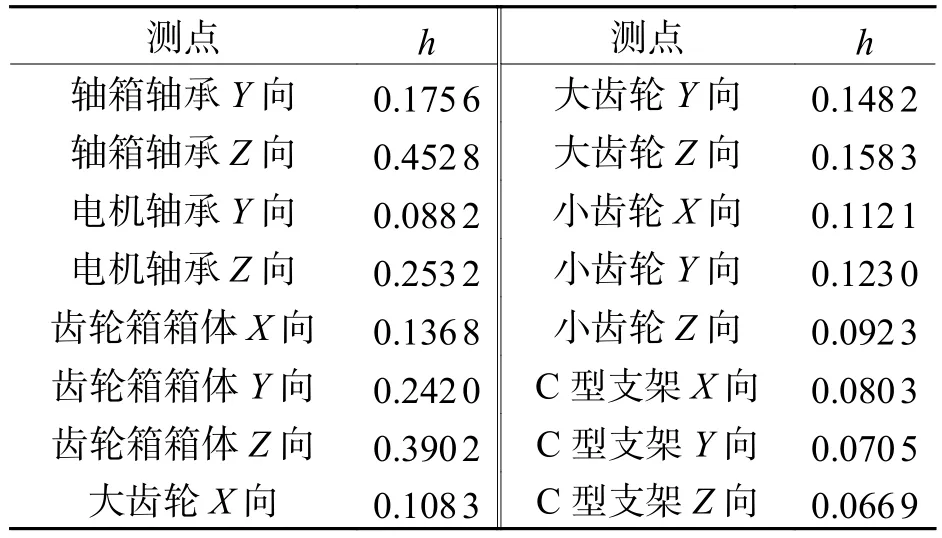
表1 核密度估计窗宽Tab.1 Bandwidth of kernel density ×g

根据核密度估计理论，在MATLAB中绘制各个关键部件沿X、Y、Z的振动加速度核密度估计概率密度函数曲线，如图2所示.

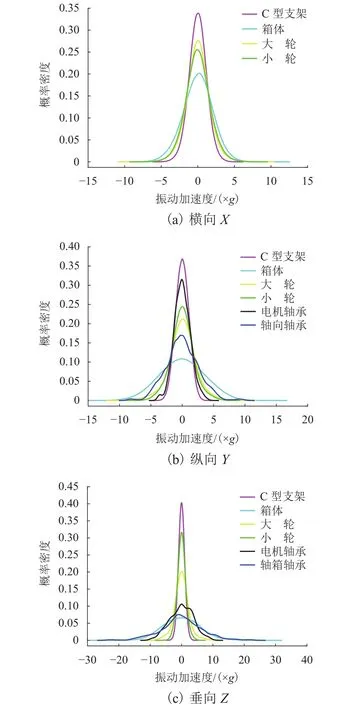
图2 关键部件振动加速度估计Fig.2 Vibration acceleration estimation of key components

2.3 传动系的振动评价

依据前文对于传动系中关键部件的振动加速度概率密度估计，参考IEC 61373—2010[11]计算出各关键部件在3个方向上概率为99.75%的均方差值，如表2所示.

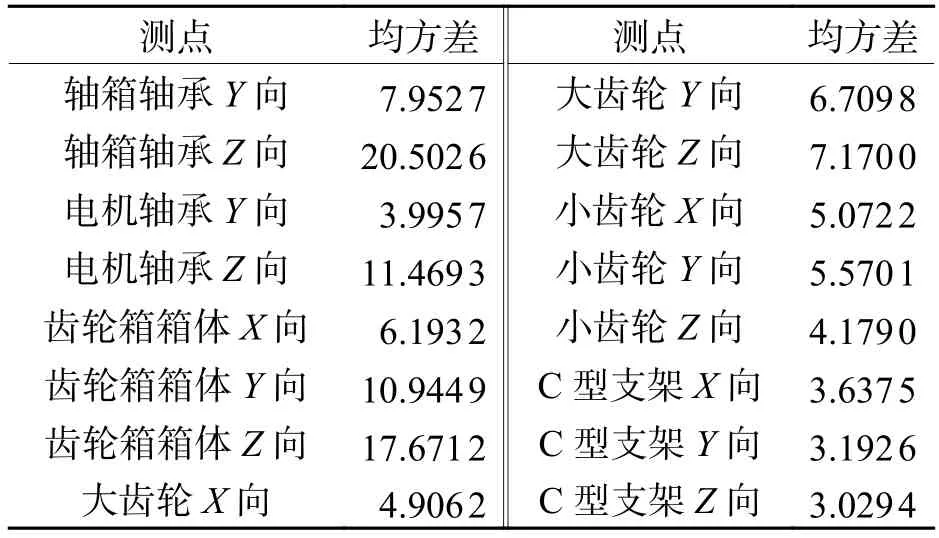
表2 振动加速度均方差统计值Tab.2 Vibration acceleration 3 σ statistics ×g

整体来看，从振动加速度的均方差值可以看出，轴箱轴承、齿轮箱以及电机轴承的垂向振动加速度最强，概率99.75%的均方差值分别为20.502 6倍、17.671 2倍、11.469 3倍重力加速度.

基于振动加速度的大小及分布范围进行振动评价：

1） 轴箱轴承和电机轴承，通过核密度估计曲线可看出：轴箱轴承与电机轴承的垂向振动响应更为剧烈；轴箱轴承的纵向振动加速度与垂向振动加速度基本上分布在10倍及25倍重力加速度以内，轴箱轴承同时承受传动系及轮轨传递上来的振动，受行驶环境影响也比较大，故加速度响应数值分布范围较大；电机轴承的纵向振动加速度与垂向振动加速度基本上分布在4倍及10倍重力加速度以内.电机轴承因电机转子的高速运转会产生一定的振动，另外，小齿轮与大齿轮相互啮合的过程中也会产生振动并传递给电机轴承，电机轴承在垂向振动的加速度响应数值分布范围也较大.

2） 齿轮箱箱体的横向振动、纵向振动及垂向振动的振动响应依次递增，分别分布在5倍、10倍、20倍重力加速度以内，齿轮箱箱体的振动响应在传动系的关键部件内数值偏高，齿轮箱箱体在列车运行过程中会承受来自大小齿轮啮合、轴箱轴承以及电机等其他部件传递的振动，另外齿轮箱箱体承受多个物理场的耦合作用，工作环境复杂，也是在实际运行过程中齿轮箱裂纹故障较多的原因.齿轮箱箱体的可靠性对于传动系可靠性有关键影响.

3） 大齿轮的横向振动响应较纵向及垂向振动响应较小，纵向振动响应与垂向振动响应相当，横向振动加速度分布在5倍重力加速度以内，纵向及垂向振动加速度分布在10倍重力加速度以内.因大齿轮压装在车轴上，横向振动主要因车轴振动引起，所以振动幅度小，大齿轮在与小齿轮啮合的过程中主要引起纵向及垂向振动，所以对于大齿轮的可靠性研究过程中，大齿轮的纵向振动也不可忽略.

4） 小齿轮的横向振动响应与纵向振动响应相当，振动加速度分布在6倍重力加速度以内，垂向振动响应相对较小，主要分布在4倍重力加速度以内.小齿轮通过联轴节与牵引电机连接实现动力传递，在运行过程中，联轴节必须保证高转速传递可靠，但同时也会传递振动给小齿轮，因此小齿轮在纵向和横向的振动加速度响应值较垂向偏高，在进行传动系可靠性分析时，数据的选取需要区别于其他部件.

5） C型支架3个方向的振动加速度响应均在3倍重力加速度以内，其振动加速度的范围最小.C型支架是连接转向架构架及齿轮箱的装置，在列车运行过程中，主要承受因扭转等产生的作用反力，要求其在高负载工况下连接可靠.

2.4 最优置信区间的确定

从不同振动加速度数值所对应的概率来看，大齿轮、小齿轮及C型支架在3个方向上的振动加速度数值对应的概率基本相近，但是对于轴箱轴承、电机轴承及齿轮箱箱体不同方向上的振动加速度数值对应的概率有较大差别.

根据前面对各个关键部件的振动加速度的核密度估计，设置置信水平为99.75%，通过MATLAB确定各个关键部件的振动加速度的最优置信区间如表3所示.

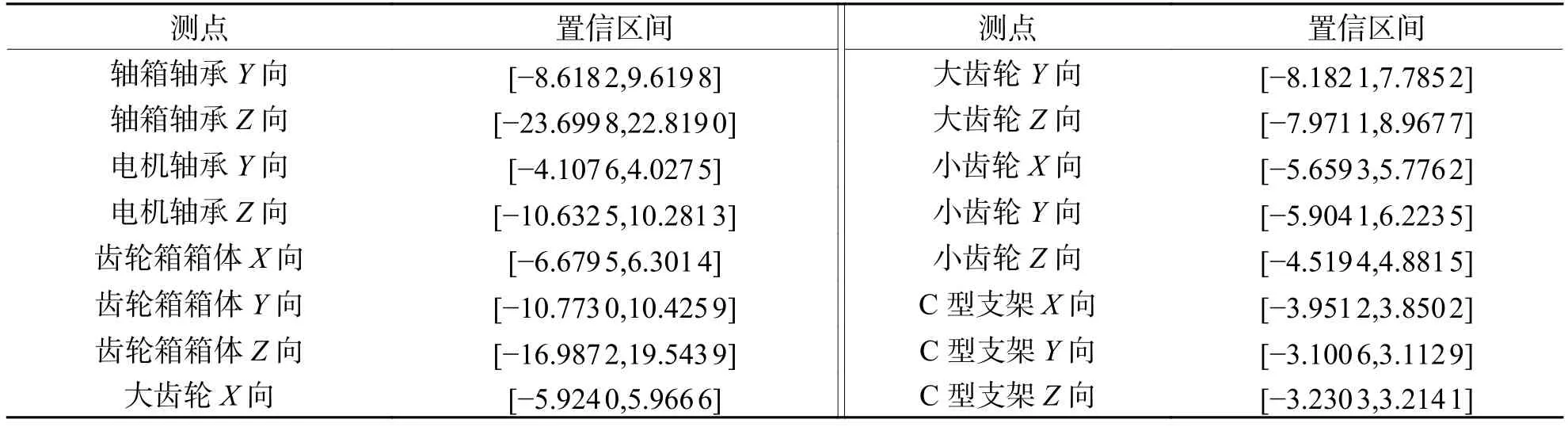
表3 最优置信区间Tab.3 Optimal confidence interval ×g

最优置信区间可以对传动系在服役过程中的可靠性评估提供参考，对动车组的振动监控装置的振动阈值提供优化参考，另外，在进行传动系前期设计及振动试验时也可以提供可靠的振动阈值参考.通过置信区间的数值可以看出，轴箱轴承、电机轴承以及齿轮箱箱体的垂向振动阈值相对较大，所以在前期设计时需格外注意相关部件的可靠性，并且在进行定期维护保养时也应该重点关注相关部件的磨损程度，以保证传动系的可靠运行.

3 高速列车传动系的可靠性分析

基于传动系的Markov模型进行可靠性分析，需要给出各关键部件的故障率及修复率.根据上文对传动系统关键部件的振动分析，小齿轮的纵向振动响应及其他各部件的垂向振动响应具有更大的数量级，包含更加丰富的信息量，可以更好地反映部件的实际运行状态，故将小齿轮的纵向振动加速度数据及其他关键部件的垂向振动加速度数据作为进行威布尔故障率参数估计的数据样本.

3.1 传动系的Markov模型

高速列车传动系的结构如图3所示.文中仅对除牵引电机外的传动系统进行分析，牵引系统可以单独进行建模分析.

图3 高速列车传动系结构Fig.3 High-speed train transmission system structure

高速列车传动系为可修复系统，可以对其进行Markov建模分析，主要针对传动系的关键部件进行分析，当某一关键部件发生故障，整个传动系就进入故障状态，并立即进行维修.

在建立传动系 Markov模型前，作以下假设：

1） 系统或部件只有正常和故障两种状态，状态间可以进行可靠性转换[12].

2） 传动系各关键部件的故障率和修复率分别设为 λ 和 µ ，且假设修复率为常数，则在 Δt内发生故 障的概率及修 复概率分别为 λ Δt和 µ Δt.另 外，在很小的时间区间内，不会发生两个及以上的状态转移.

3） 传动系的6个关键部件互相独立，在t～t+Δt时间内：电机轴承的故障率为 λ1，修复率为 µ1；轴箱轴承的故障率为 λ2，修复率为 µ2；齿轮箱箱体的故障率为 λ3，修复率为 µ3；大齿轮的故障率为 λ4，修复率为 µ4；小齿轮的故障率为 λ5，修复率为 µ5；C 型支架的故障率为 λ6，修复率为 µ 6.

4） 系统的状态设定如下：设S0为传动系的正常状态；S1为电机轴承的故障状态；S2为轴箱轴承的故障状态；S3为齿轮箱箱体的故障状态；S4为大齿轮的故障状态；S5为小齿轮的故障状态；S6为C型支架的故障状态.

依据上面的假设，建立传动系的Markov状态转移模型，如图4所示.

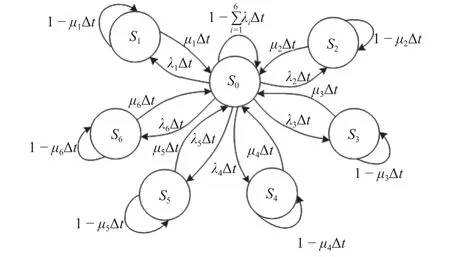
图4 传动系Markov状态转移模型Fig.4 Markov state transition model of transmission system

3.2 基于振动响应数据的故障率评估

本文中各类部件采用比例故障率模型（式（10））估计其故障率，比例故障率模型可以基于振动响应信号的特征值与故障率建立联系，适用于运行设备故障率的估计.

式中： λ0(t) 为部件的基本故障率函数；W为响应协变量； γ 为反映响应协变量对部件故障率影响的回归参数.

机械、电子类产品因磨损累积、疲劳累积等形成的故障服从威布尔（Weibull）分布[13].本文中各个部件的基本故障率函数取威布尔分布故障率函数，如式（11）.

式中： β 为形状参数； η 为尺度参数.

威布尔比例故障率模型中的响应协变量W的本征维数可以依据对关键部件时、频域高维特征向量进行的维数约简结果来确定.其中，小齿轮、大齿轮、齿轮箱箱体、C型支架及电机轴承的本征维数为2，轴箱轴承的本征维数为3.因篇幅限制，此处的求解过程不作详细说明.

响应协变量在本研究中选用峭度值、均方根值及峰值因子这3种时域无量纲特征值，在MATLAB中对采集的数值进行特征值的计算，依据本征维数的不同选取的特征值有所不同，轴箱轴承选择峭度值、均方根值及峰值因子为响应协变量，其余关键部件选择峭度值及均方根值为响应协变量.

截取某段时间的振动响应数据计算各部件的响应协变量，即振动特征值，如图5所示.

图5 振动特征值Fig.5 Vibration characteristic values

根据小齿轮的纵向振动加速度响应及其他关键部件的垂向振动加速度响应，依据极大似然估计确定传动系各个部件故障率函数模型的参数值如表4所示，、、为各部件依据响应协变量的选取情况确定的威布尔比例故障率中的回归参数.依据威布尔故障率模型预测各关键部件的故障率如图6所示，并取某时刻的实时故障率用于可靠性分析，如表5所示.

图6 故障率Fig.6 Failure rate

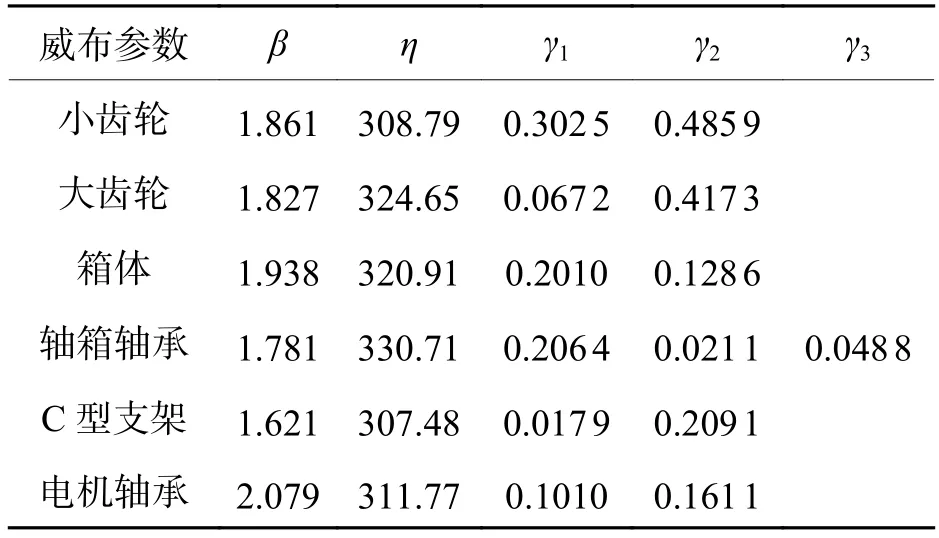
表4 威布尔模型参数估计数值Tab.4 Weibull model parameter estimates

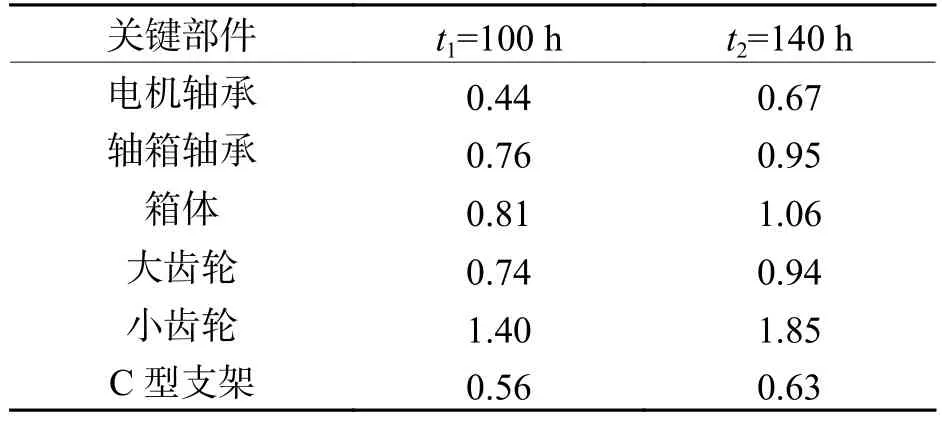
表5 各关键部件实时故障率Tab.5 Real-time failure rate of key components ×10-2

3.3 传动系的可靠性分析

根据前面建立好的Markov状态转移模型，传动系的状态转移差分方程组为

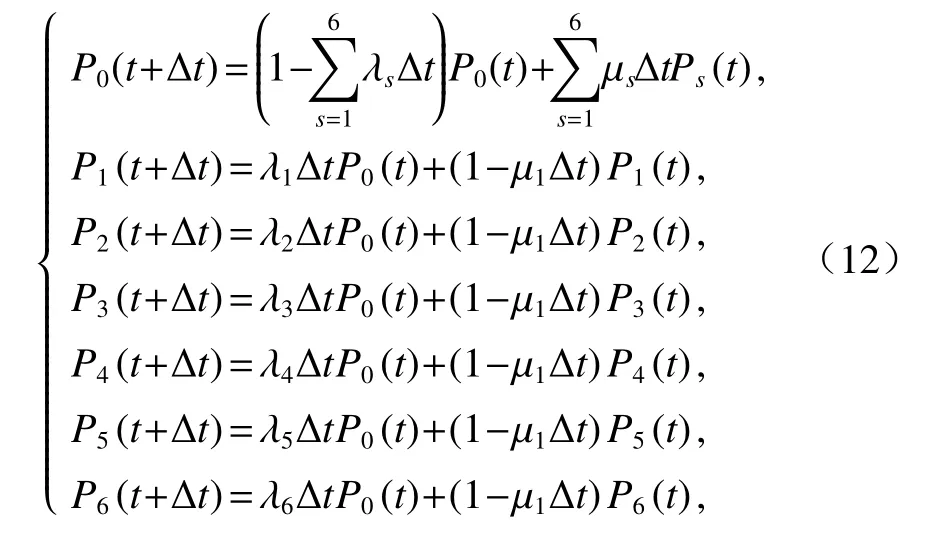
式中：Ps(t)(s=0,1,2,3,4,5,6)为传动系在时刻t处于状态s的概率，为传动系经过的状态转移概率[14].

在研究中为便于计算及对比，取关键部件的修复率为统一数值，分别取关键部件的修复率为0.005，0.050、0.100，在MATLAB中编程计算在t1=100h及t2=140h 传动系处于各状态的概率如图7所示.

基于前文Markov建模的假设条件，P0(t) 即为系统的稳态可用性，从图7中可以看出：各个部件不同的故障率大小及维修率的高低影响部件本身及系统的稳态可用性，并且各部件故障率及维修率的大小对传动系的影响要远大于对部件本身的可用性的影响；当关键部件的修复率为0.005时，系统的稳态可用性降至20%以下，并且下降速度很快；当关键部件的修复率提升至0.100时，系统的稳态可用性能够达到70%以上，并且在较短的时间内达到比较稳定的数值，极大地提高了高速列车传动系运行的可靠性.当关键部件的故障率提高30%左右时，在相同修复率的情况下，系统的可用性会在短时间内下降10%左右，严重影响高速列车运行的安全性及运行成本.所以准确统计高速列车行车过程中的故障及修复过程，提升修复效率对提升高速列车传动系的可靠性有非常积极的影响.高速列车的运行管理及检修制度也直接影响故障率及维修率的变化，基于高速列车传动系在运行中的实时状态，监测系统故障率的变化，实时估测系统的运行可靠性对于现行检修制度的优化具有重要的参考意义.

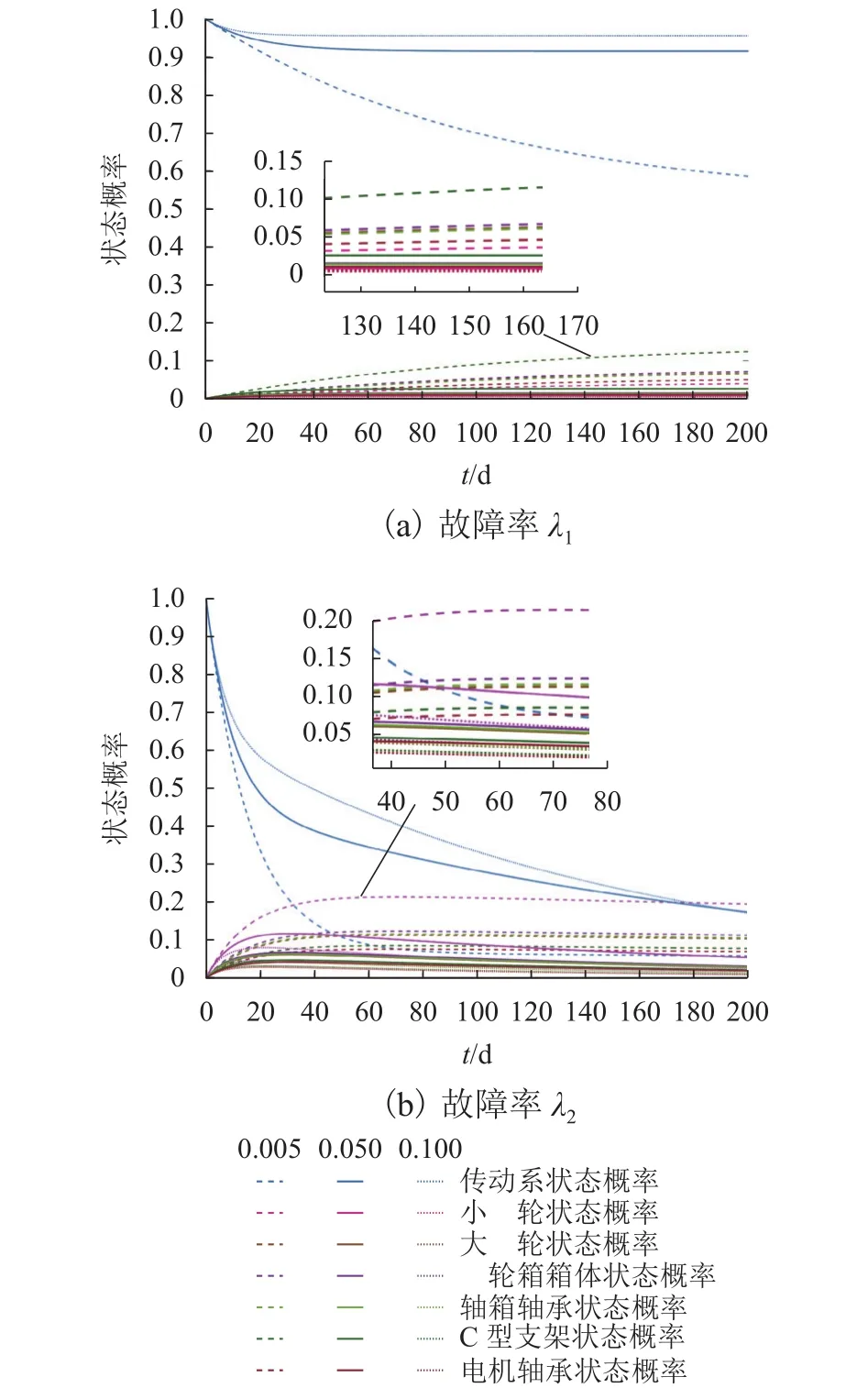
图7 传动系状态概率Fig.7 Transmission system state probability

4 结 论

1） 通过KDE方法对高速列车传动系进行基于实测振动响应数据的振动评价，根据得到的振动响应核密度估计概率密度曲线可以明确高速列车传动系各关键部件在实际运行中承受振动的剧烈程度，此方法可以展开应用于各类车型在各类实际路况中的振动评价.

2） 根据实测振动加速度均方差值能够确定高振动强度部件，为高速列车可靠性设计及评估提供参考，通过协调各部件的可靠寿命来保证整体的使用寿命.基于实测数据计算得到的传动系振动评估的建议限值能够为实际服役车辆振动监测提供可靠的评价标准及优化参考，通过实时数据对比对部件进行故障检测，这对于提高整车的使用寿命及运行可靠性都有重要意义.

3） 基于实时监测数据分析确定关键部件的故障率，结合关键部件的修复率，建立系统的Markov模型实时评估系统的稳态可用性，部件的故障率及修复率对系统的可靠性有至关重要的影响.基于使用过程中的实时监测数据分析，实现传动系故障实时监测判定，有益于高速列车的状态监控维修，这对于提高故障检测率及维修率有积极的影响.通过合理的维修方式、优化的作业组织、强化作业人员培训、故障及维修信息的合理统计分析等手段来提高维修率，可以大幅度提高系统的使用可靠性的同时，也实现了高速列车检修制度的改进.