基于光流融合快速特征提取的视觉/惯性定位方法

赵锦阳

北京信息科技大学高动态导航技术北京市重点实验室，北京 100101

0 前言

近年来，导航技术有了快速的发展，然而在一些特殊环境下，例如地震后的废墟、灾害后的矿洞、地下车库等地下遮蔽空间，环境的封闭性导致定位困难。由于惯性传感器有着成本低、重量轻、易携带等优点，受环境的封闭性影响较小，因此，在地下遮蔽空间内，惯性定位技术成为人员定位的首要选择。由于惯性器件本身存在零漂稳定性、噪声、随机游走等误差，导致其在长时间运行时漂移误差不断累积，从而导致定位不准确，而相机采集的数据基本不会有漂移，使用相机辅助惯性传感器可以有效修正惯性传感器的漂移误差[1]。因此，采用由相机与惯性传感器融合的视觉/惯性定位可以解决在地下遮蔽空间内人员定位的难题。

视觉/惯性定位技术目前较为主流的有V-SLAM（Visual-Simultaneous Localization And Mapping）、视觉惯性里程计等。视觉惯性里程计是一种由相机（如单目、双目、深度摄像头等）获取图像信息，惯性传感器（IMU）采集惯性信息，将视觉信息与惯性信息进行融合，对相邻图像之间的相对位移与姿态进行估计，从而获得传感器运动的方法。按照融合信息的方式，视觉惯性里程计（Visual Inertial Odometry，VIO）分为基于滤波方法与基于优化方法。基于滤波的方法采用滤波技术（如卡尔曼滤波、扩展卡尔曼滤波、无迹卡尔曼滤波等）融合视觉信息与惯性信息；基于优化的方法采用非线性迭代技术融合视觉信息与惯性信息。按照相机状态与IMU状态是否进行合并分析，视觉惯性里程计分为基于紧耦合与基于松耦合两种方案[2-5]。在松耦合方案中，VIO对相机与IMU进行单独的运动估计，分别计算位姿结果，然后对结果进行融合；在紧耦合方案中，VIO在进行状态估计时将IMU与相机状态进行结合，共同构建运动方程和观测方程。

传统MSCKF方法[6]在视觉前端采用Two Point Ransac提取算法，通过在前后帧跟踪特征点时进行特征匹配，去除不满足双目极限约束的特征点。此算法优点是筛选过程简单，算法复杂度较小，运行时占用系统内存小；缺点是在光照较差，相机运动过快导致图像模糊等弱纹理环境下，简单的筛选机制无法保证优质的特征点筛选率，从而导致累计误差的问题。

为解决地下遮蔽空间内，弱纹理环境下视觉/惯性定位方法特征点提取、追踪困难问题，提出一种基于联合光流法的视觉/惯性定位方法。本文采用SURF（快速鲁棒性特征）提取算法[7-8]，通过在特征提取时构建Hessian矩阵，构建高斯金字塔对特征点进行提取，具有取得更好的特征提取速度与特征提取精度，随后利用LK光流法对特征信息进行追踪。信息融合部分：利用IMU信息进行状态与协方差预测，将相机的位姿信息加入特征向量和协方差矩阵中对状态信息进行扩增。通过特征信息构建观测模型对状态预测进行修正。在特征点信息消失或滤波状态消失时，对卡尔曼滤波器进行更新。本文算法流程如图1所示。

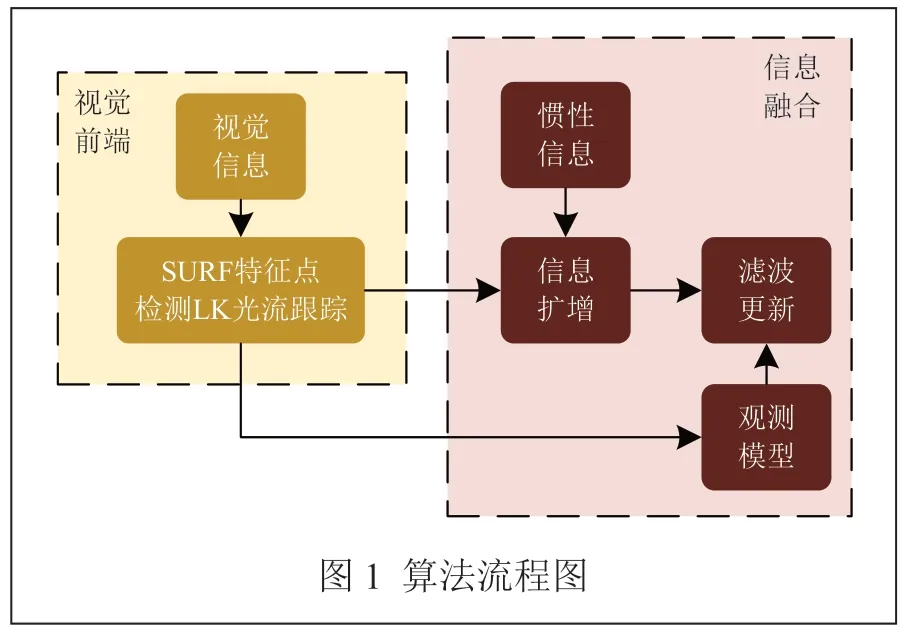
1 前端图像信息处理

1.1 SURF算法

1.1.1 构建Hessian矩阵

SURF算法通过求取特征点的Hessian矩阵，经过滤波求得矩阵行列式，利用行列式图进行图像近似。在一个尺度为σ的图像中，若某一个像素点的横坐标为x，纵坐标为y，则这个像素点的坐标为f(x, y)，它的Hessian矩阵为：

进行类比，可以求出这幅图像中每一个像素点的Hessian矩阵，进行高斯滤波后得到：

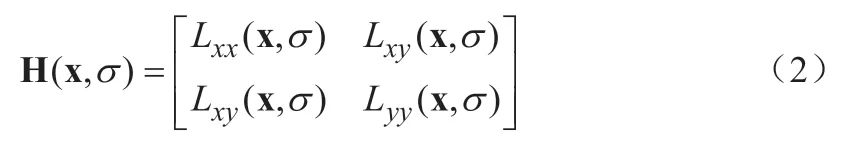
其中，Lxx(x,σ)、Lxy(x,σ)、Lyy(x,σ)——滤波后图像在各个方向上的二阶导数， 求得矩阵行列式的值为：

为了加速卷积的效率，使用方框滤波代替二阶高斯滤波。用方框滤波替代表示之后，令Lxx、Lxy、Lyy记为Dxx、Dxy、Dyy，则Hessian矩阵行列式为：

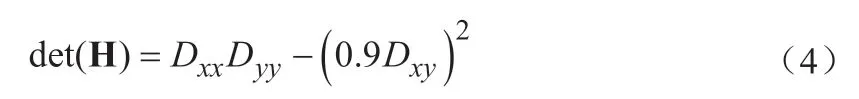
其中，0.9——权重系数。

如此可得一张近似Hessian矩阵行列式图，通过改变不同尺度的高斯模板即可构建高斯金字塔。

1.1.2 确定特征点方向

以特征点为中心，在尺度为σ的范围内构建以6σ为半径的圆，统计在60°扇形内，所有点的x轴方向上与y轴方向上haar小波特征总和。将扇形每经过一定的时间间隔进行旋转，直到最后得到一个最大值，即为特征点的主方向。

1.1.3 特征点描述与匹配

在特征点的附近选取一个正方形框，将该框16等分，划分为16个子区域，分别统计每个子区域内25个像素的haar小波特征：其中各项分别是水平方向之和、水平方向绝对值之和、垂直方向之和与垂直方向绝对值之和。四维描述向量为：因此SURF的描述子共有64维。

SURF算法衡量两个特征描述子相似度的方法是计算其相隔的欧式距离。例如，在寻找A、B两幅图像之间的相似特征点时，将图像A中的一个特征点与图像B中所有特征点进行相似度比较，欧氏距离最小的为相似点。

1.2 LK光流

LK光流法认为不同时间点对应着不同的图像[9]。因此，将图像看做时间的函数I(t)。在t时刻，某个位于(x, y)处的像素，灰度表达式可以写成I(x, y, t)。通过使用这种函数表达，图像成为了关于时间与位置的函数，它的值域就是图像中像素的灰度。

由于相机在传输信息时传输的是连续帧的图像，因此可以认为这些图像是随时间连续变化的。对于t时刻位于(x, y)处的像素，设在t+dt时刻它运动到(x+dx, y+dy)处，则：

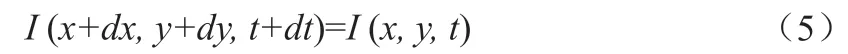
对左边进行泰勒展开，保留一阶项，得：

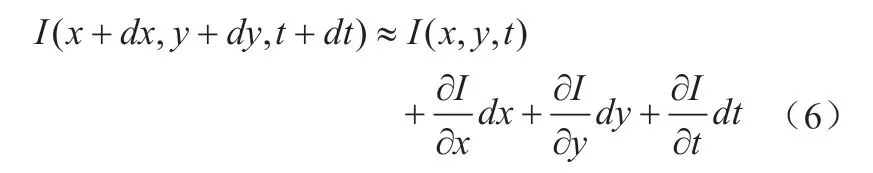
由LK光流法中灰度不变假设可得，下个时刻的灰度保持不变，与上一时刻的灰度值相等，从而：

两边除以dt，得：

将图像灰度对时间的变化量记为It，写成矩阵形式为：

由LK光流法中的空间一致假设可得，同一个窗口内的所有像素具有相似的运动。设一个窗口大小为ω×ω，则其含有ω2个像素，则：

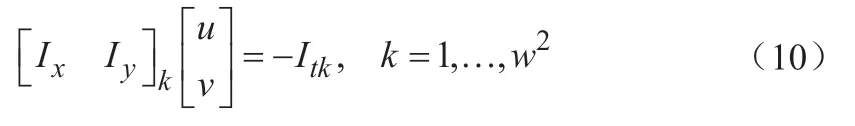
令：

则方程变为：

求得其最小二乘解为：

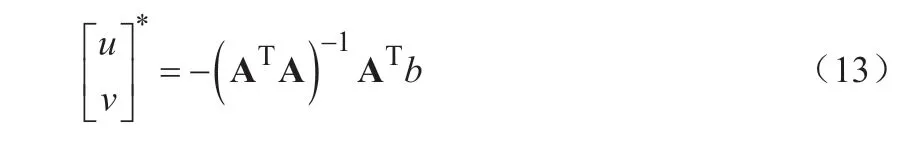
即可得到像素在图像间的运动速度u、v。

2 信息融合框架

2.1 信息扩增

由四元数Iq表示惯性坐标系中的转动。向量 GvI∈R3和GPI∈R3表示惯性坐标系下的速度和位置。向量bg∈R3和ba∈R3分别表示陀螺仪和加速度计的测量偏差。则IMU的状态参数表示为：

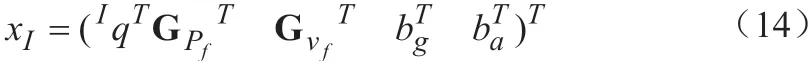
由于使用实模态会导致协方差矩阵的奇异性，从而导致IMU的状态误差可定义为：

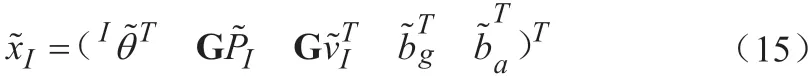
其中，表示误差四元数。将相机的状态加入状态向量中，误差状态可以写作：

其中，——每个相机的位姿误差。

IMU状态的连续动态数学模型为：

其中，∈ R3和∈ R3是 陀螺仪和加速度计的无偏差测量值；R(I) 用 于将四元数转换为旋转矩阵；Ω() 可 以写作：

其中，[] 表 示对应于的斜对称矩阵。误差惯性测量单元状态的线性动态方程为：

为了解决惯性测量单元测量时间的离散问题，采用龙格-库塔数值积分进行状态转移。由于惯性测量单元状态的不确定性，转换矩阵和噪声协方差矩阵为：

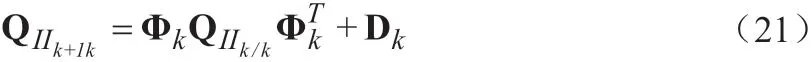
状态的协方差矩阵可分为：

完全不确定性转移Qk+1/k可以表示为：

当接收到新的相机图像时，状态进行扩增，增广协方差矩阵为：

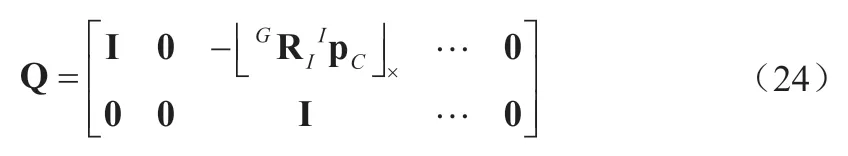
2.2 观测模型

由于在状态预测的过程中，误差会随着时间积累，因此，引入相机的观测值对系统状态进行修正。若单个特征点fj已经在图像中被观测，并且观测值中包含有特征点在像素坐标系下的坐标由于双目摄像头的姿态不同，所以同时左摄像头和右摄像头的姿态分别记录为和。 双目测量表示为：

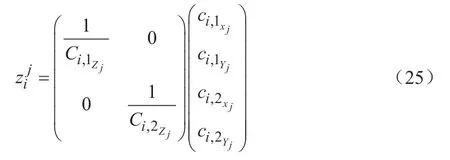
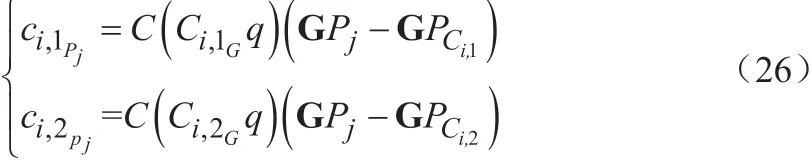
根据估计的相机姿态，使用给定的最小二乘法计算相机在世界坐标系中的位置。为了更新残差的协方差，对观测函数在当前状态进行线性化，测得的残差rij的近似值可写成：

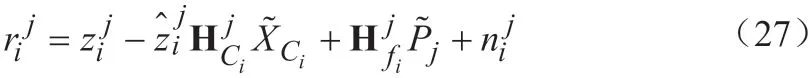
其中，——测量噪声；

计算追踪过程中的残差，通过叠加相同字符fj的各种观察值：

2.3 滤波更新

滤波更新是算法中的最后一步，在两种情况下算法会执行滤波更新步骤：（1）一些特征点丢失；（2）当相机状态的数量达到滑动窗口的上限。执行滤波更新时，所有的特征点信息被用来约束和修正误差。对每一个追踪的特征点计算对应的残差与特征点位置误差并添加到总体状态中，修正累积的误差。

3 实验分析

为了验证算法的整体性能，本文在各数据集上对其进行了测试，实验数据集采用EuRoC室内数据集，IMU采样频率为200 Hz，相机采样频率为20 Hz。EuRoC数据集由苏黎世联邦理工学院开源，采集自微型飞行器上的视觉惯性传感器，数据集场景为室内机器人大厅与厂房，较好地还原了地下空间光照较差、图像模糊等问题。实验设备为笔记本电脑，i59代芯片，rtx960显卡。轨迹处理使用EVO评测工具，对算法输出的轨迹与数据集中真实轨迹进行对比，计算估计轨迹与真值的误差。

分别计算本文方法与MSCKF在不同数据集的运行过程中的平均单帧处理时间，并记录进行特征点识别时的特征识别效果，进行对比，其结果如图2、图3所示。

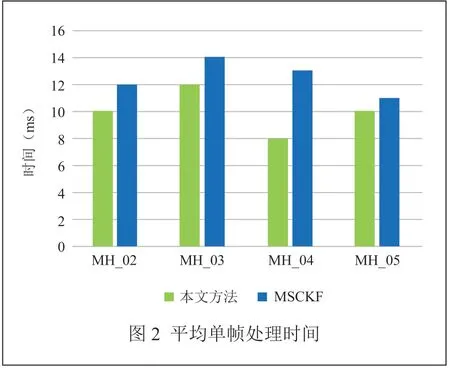
由图2可以看出，相较于MSCKF前端Two Point Ransac提取算法，本文方法在单帧处理时间上平均快了约3 ms，证明本算法具有更快的特征点提取速度。图3中（a）、（b）两图分别是本文方法与MSCKF的特征点识别效果，在视觉信息模糊、弱环境纹理、光线较暗环境下，本文拥有更好的特征点识别精度与效果。

将运行数据集后计算出的位姿使用EVO评估工具进行处理，与真实轨迹对齐，并与MSCKF算法进行对比，对比结果分别如图4 ～图7所示。

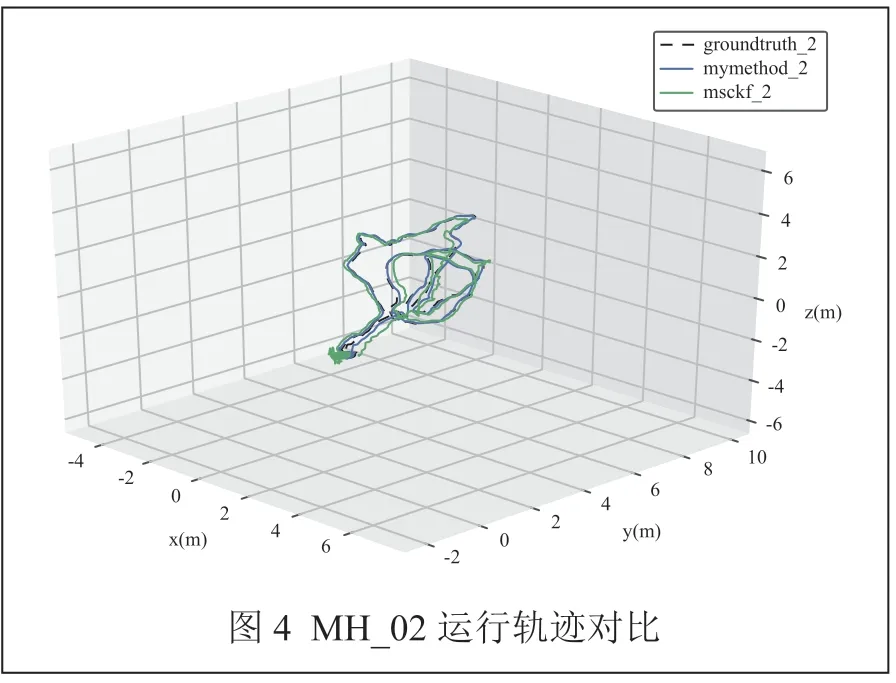
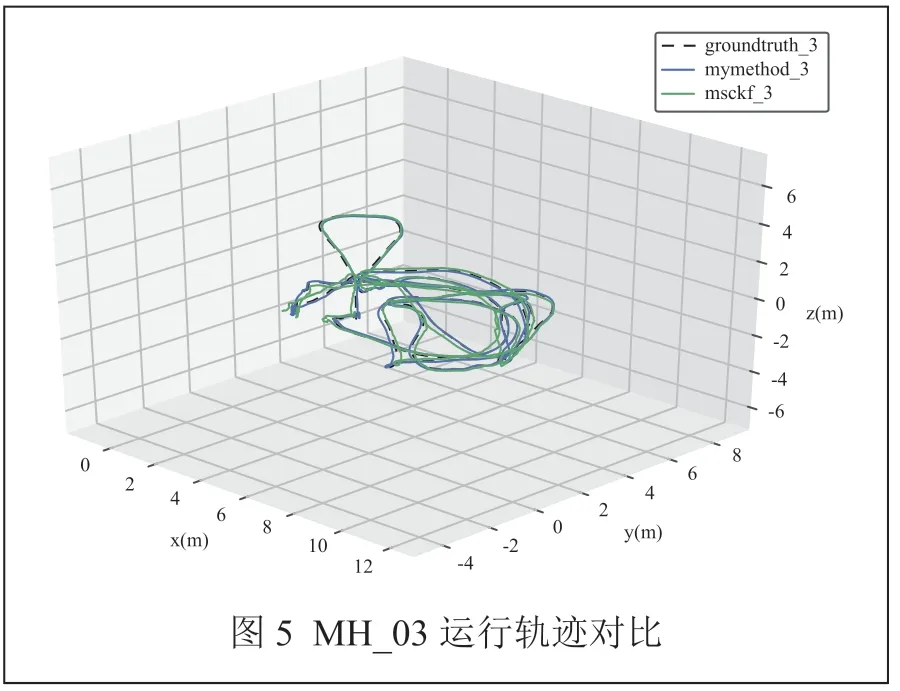
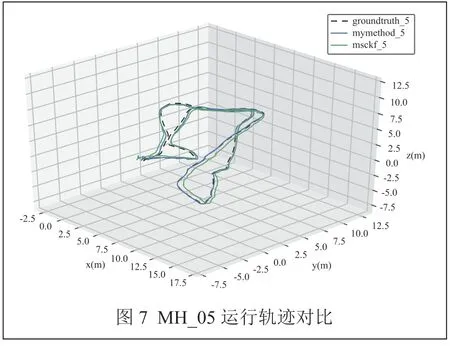
图中虚线为数据集中真实轨迹，蓝色、绿色线条分别为本文方法与MSCKF算法输出估计值。相较于MSCKF算法，本文估计轨迹更为精确，与真值偏离程度更小。

通过使用EVO评测工具对算法输出轨迹与真值间的偏差进行分析，计算出算法输出位姿与真值间的轨迹误差与均方根误差，结果如表1、表2所示。

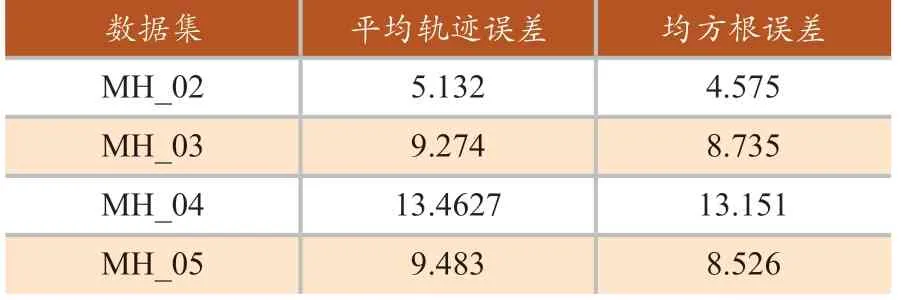
表1 本文算法误差（单位：m）

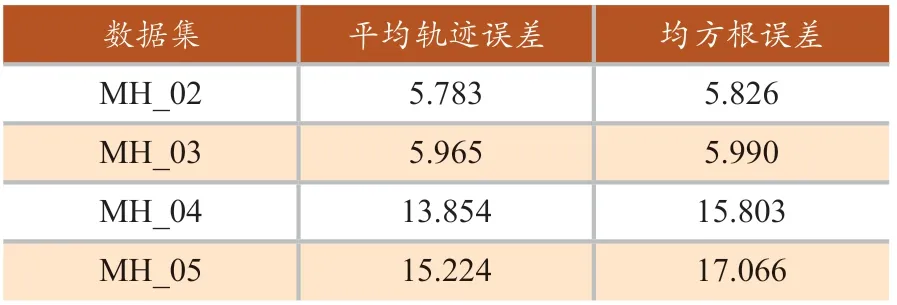
表2 MSCKF算法误差（单位：m）

平均轨迹误差代表估计轨迹相较于真实轨迹的偏离程度，值越低代表估计轨迹精度越高；均方根误差代表估计轨迹的离散程度，值越低表明估计轨迹离散越小，系统稳定性越高。以平均轨迹误差与均方根误差作为精度标准，本文算法相较于MSCKF算法，平均轨迹误差平均减少8%，均方根误差平均减少21%。证明本文算法相较于MSCKF算法拥有更为精确的位姿输出。

为了进一步验证本文算法的性能，采用MH_05数据集，与另一种同为基于滤波的VIO算法ROVIO[10]进行对比，轨迹对比结果如图8所示，精度对比如表3所示。相较于目前主流的ROVIO算法，本文算法有更低的误差，更高的准确性，证明了本文算法的优越性能。

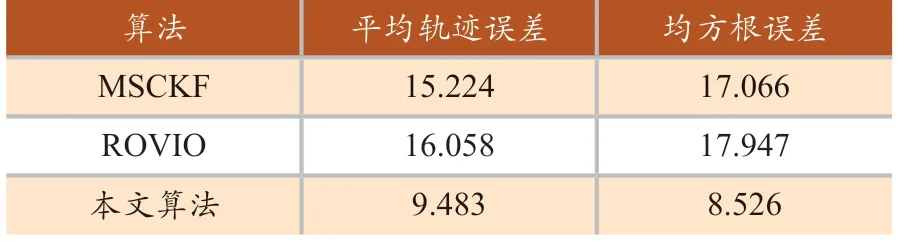
表3 算法误差对比（单位：m）

4 结束语

针对弱纹理环境下，视觉/惯性定位方法特征点提取、追踪困难问题，本文提出了一种视觉/惯性定位方法，通过SURF提取特征点，LK光流法对特征点进行追踪，将视觉信息与惯性信息进行紧耦合状态分析，输出位姿估计结果。通过对EuRoc数据集中的图像部分进行仿真分析，与MSCKF算法对比，验证了本文方法具有更快的单帧处理速度与更高的特征点识别精度，证明了本文方法在前端视觉处理部分在弱纹理环境下具有更好的适应性与鲁棒性。对输出位姿进行保存，与真实轨迹对齐，并与MSCKF、ROVIO进行对比，验证本文方法能够实现更为精确的位姿估计，且在弱纹理环境下具有更好的定位精度，证明了本文方法的有效性，相较于现有的视觉惯性里程计算法具有显著优势。在工业视觉惯性导航领域具有应用前景，为应急救援、位置服务等领域提供了新的思路。