启发式狼群算法求解不相关并行机调度问题
荀洪凯,陶翼飞,罗俊斌,何 李
(1.昆明理工大学机电工程学院,云南昆明 650504;2.昆明昆船逻根机场物流系统有限公司,云南昆明 650236)
0 引言
并行机调度[1](Parallel Machine Scheduling,PMS)在生产制造领域应用广泛,如半导体加工、注塑成型加工、纺织加工、光刻加工、卷烟加工等,并行机调度问题也已经被证明为一类经典的NP-hard 问题。而在实际生产加工过程中,由于并行机加工能力不同,需要考虑工件加工分配问题,导致其复杂程度更高,求解难度更大,从而对不相关并行机调度(Unrelated Parallel Machine Scheduling,UPMS)问题的研究具有更重要的理论意义和应用价值。
近年来,不相关并行机调度问题被广泛研究,目前并行机调度问题大多采用启发式算法或其它智能优化算法进行求解。通过改进传统智能优化算法进行求解仍然是重要的研究方向,例如对遗传算法的改进方面,Abreu 等[2]提出一种混合遗传算法用于解决具有序列相关设置时间的不相关并行机调度问题;Xuan 等[3]将遗传算法和模拟退火算法结合,开发了一种新的遗传模拟退火算法,以解决具有不相关并行机的混合流水车间调度问题。近年来,不少新算法相继被提出,蚁狮优化算法[4]、混合差分进化算法[5]、混合多目标教—学优化算法[6]、混合启发式算法[7]等,都被应用到求解并行机调度问题。同时,很多组合优化算法也被提出,Zhang 等[8]提出一种结合列表调度、启发式最短设置时间优先规则和最早完成时间优先规则的组合进化算法以解决具有有限工人资源和学习效应的不相关并行机调度问题。从当前研究可以看出,通过算法融合,以及有针对性地提出一些新算法,可以有效弥补传统算法所存在的不足,并且为求解不相关并行机调度问题扩展了研究方向,本文提出一种算法融合的方式以优化并行机调度问题。
目前,针对不相关并行机调度问题的研究已经比较成熟,但在搜索效率方面并未得到实质性提升,代招等[9]通过利用混沌映射和反向学习策略生成初始种群,改善初始种群的质量,求解以最小化最大完工时间为目标的柔性作业车间调度问题;顾文斌等[10]提出一种新的启发式算法提升初始种群质量,改善搜索效率。目前,不相关并行机调度问题中搜索效率提升方法相关研究较少。在算法选择方面,吴虎胜等[11]提出一种狼群算法(Wolf Pack Algorithm,WPA),该算法利用不同的搜索机制对狼群进行搜索,结构简单、寻优效率高,主要应用在多旅行商问题[12]、柔性作业车间调度问题[13]以及置换流水车间调度问题[14]中。目前,狼群算法已经解决了多种调度问题,但在并行机调度问题中的研究并不完善。本文设计启发式算法旨在提高其搜索效率,选用狼群算法目的是保留算法并行性等优势。
综上所述,本文在求解不相关并行机调度问题时以最小化最大完工时间为优化目标,首先,为提高搜索效率,提出一种启发式算法,选择合适的工件分配原则,将启发式算法得到的种群与随机生成的初始种群共同进行优化;其次,结合狼群算法的显著特点以及在求解调度问题方面的优势,对狼群算法智能行为机制中邻域搜索方式进行设计,局部邻域搜索与全局邻域搜索相结合,使搜索效率达到最大化,最终通过不同规模不相关并行机调度问题算例进行仿真优化实验,证明所提出的启发式狼群算法(Heuristic Wolf Pack Algorithm,HWPA)求解不相关并行机调度问题切实有效,与其它优化算法相比该算法拥有更高的求解效率和精度。
1 问题描述
本文研究不相关并行机调度问题,该问题可以描述为:设N为待加工工件集合,M为并行机机器集合,每个工件只需在一台机器上加工,同一台机器在同一时间只能加工一个工件,并且每个工件在每台机器上加工时间不同,每个工件之间没有先后顺序约束,即所有工件具有相同的优先加工级,每个工件被加工的概率相同。假设工件j在机器i上的加工时间为t(i,j),定义工件j在机器i上的广义加工时间为x(i,j)t(i,j),其中x(i,j)=1 时表示工件j在机器i上加工,否者x(i,j)=0。定义工件j在机器i上的加工初始时间为T(i,j),工件j+1 在机器i上的加工初始时间为T(i,j+1)。总完工时间用C表示,最终求解目标为最小化最大完工时间,即minCmax。并行机调度示意图见图1。
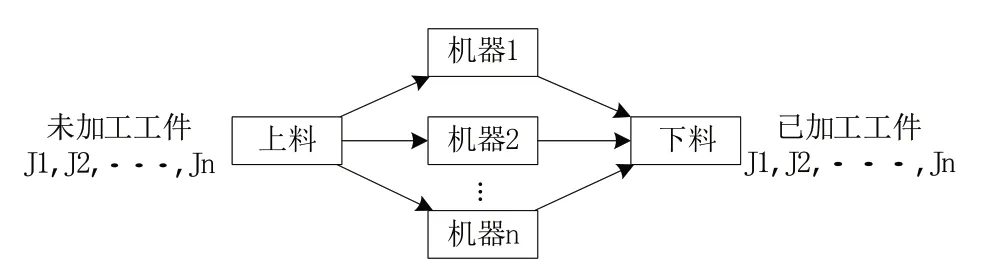
Fig.1 Parallel machine scheduling schematic图1 并行机调度示意图
目标函数为:

约束条件为:
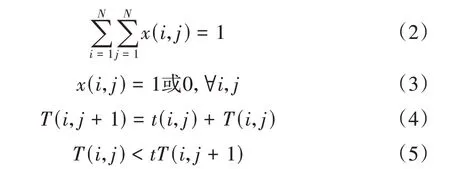
式(1)为模型中最小化最大完工时间,即目标函数;式(2)确保每个工件只能由一台并行机完成加工;式(3)定义了变量的取值范围,式(4)规定工件在机器上加工未完成时不能更换工件;式(5)保证每台机器上的工件按照一定的顺序进行加工。
2 启发式狼群算法
为有效求解不相关并行机调度问题,本文提出一种启发式狼群算法。该算法主要由两部分组成:①针对不相关并行机调度的特点,对算法初始种群通过启发式算法进行调整;②在迭代过程中,不同类型的狼群设置不同的邻域搜索方式。算法流程如图2所示。
具体步骤如下:①设定启发式算法中每代个体数i、规模数及迭代次数i;②初始化种群,将随机初始化的种群与启发式算法寻优得到的种群共同组成初始种群;③狼群分类,对初始化种群中的所有个体进行译码、仿真并计算其适应度值,按照计算出的适应度值以及选定的规模数进行相应分类;④探狼游走,分类后的个体中探狼个体根据下文游走机制进行相应的邻域搜索,并计算其适应度,观察最优解是否得到更新;⑤头狼召唤,分类后的猛狼个体根据召唤机制进行相应的邻域搜索,计算搜索后的个体适应度,判断最优解是否需要更新;⑥狼群围攻,将最优个体以外所有个体根据围攻机制进行全局邻域搜索,计算出本次迭代中所有个体适应度值并找到最优解;⑦判断最大迭代次数是否完成,若是,则算法结束,输出最优个体编码即为最优解,若否,则执行步骤③。

Fig.2 Flow of HWPA图2 启发式狼群算法流程
2.1 初始种群生成
在狼群优化算法中,如果仅用随机方式生成初始种群,将增加种群迭代次数,因此本文在初始化种群时提出新的启发式算法,流程如图3所示。
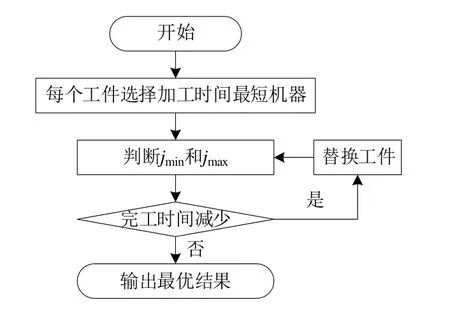
Fig.3 Flow of heuristic algorithm图3 启发式算法流程
mint(i,j)表示工件i在机器j上的最短加工时间,用jmin表示加工时间最短的机器,用jmax表示加工时间最长的机器,Nj表示机器j上加工工件集合,Njmax表示加工时间最长的机器上所加工工件集合。tj表示工件i在两台机器上加工时间差值。

式(6)表示机器j的总加工时间,式(7)表示加工时间最长机器的加工时间,式(8)表示工件i在总加工时间最长的机器和总加工时间最短的机器上加工时间差值最小,其中i∈Njmax。
启发式算法流程如图3 所示,具体步骤如下:①分别选出加工工件时间最短的机器;②确定jmin和jmax,计算出t(jmax)即是此时总完工时间;③根据式(6)和式(7)找到Njmax,并根据式(8)找到可以替换加工机器的工件i并进行替换;④重新计算总完工时间,判断总完工时间是否减少,若总完工时间减少则进行工件替换,并重复步骤②至④,若总完工时间增加则停止运行算法。
给出一个示例进行说明,先为每个工件选择加工时间最短的机器,此时甘特图如图4所示。
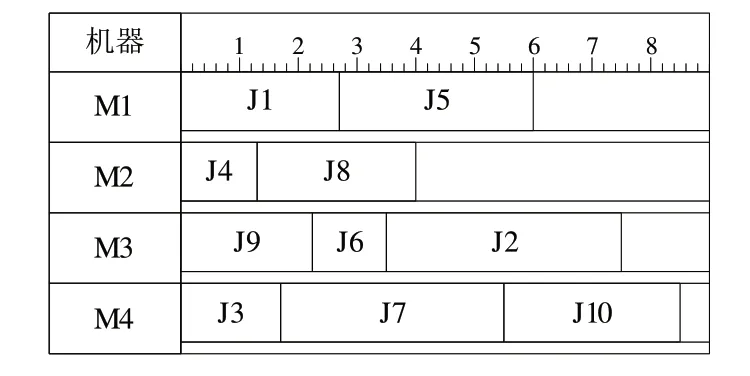
Fig.4 10×4 Gantt chart before adjustment图4 10×4调整前甘特图
根据仿真后的结果,找到最早和最晚完工机器,考虑将M4 上的工件转移到M2 机器上进行加工,此时可以选择的工件有J3、J7、J10。如图5 所示,根据这3 个工件在M2和M4 上加工所用的时间差决定将增量最小的工件J3 分配到M2上加工。
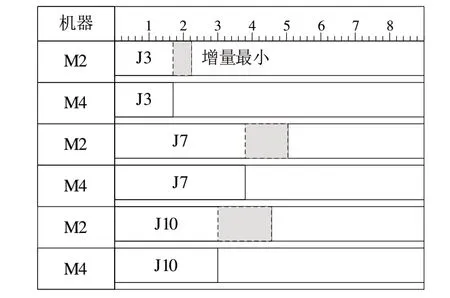
Fig.5 Time increment before and after adjustment图5 调整前后时间增量
最终调整后得到如图6 所示甘特图,此时总的完工时间减少,可以继续进行调整,直到总的完工时间不再减少为止。

Fig.6 10×4 adjusted Gantt chart图6 10×4调整后甘特图
2.2 编码及译码
本文采用单链编码方式,首先用工件编号给出工件的加工顺序,其次用大于工件编号的数字将排好的加工顺序进行分隔,进而确定工件的加工机器。这种编码方式能够使编码更简洁,减少计算次数。
根据编码方式,译码步骤为:①将分隔数字找出;②确定工件加工顺序,同时将工件分配到相应待加工机器。
例如:在7 个工件,3 台并行机的加工过程中,编码[5 7 3 8 4 2 9 6 1]中数字8 与数字9 代表分隔数字,工件加工顺序为编码先后顺序。并行机1 加工工件5、7、3,并行机2加工工件4、2,并行机3加工工件6、1。
2.3 种群适应度
本文研究的是以最小化最大完工时间为目标的不相关并行机调度问题,用时越少,适应度越高,因此种群的适应度f用所有工件加工完成时间的倒数扩大100 倍代替,即:

2.4 智能行为设置
根据狼群算法以及不相关并行机调度的特点,设计新的智能行为机制。
(1)选择机制。在迭代过程中,迭代后的最优个体优于迭代前最优个体,则进行更新。
(2)游走机制。针对种群中部分次优个体种群进行邻域搜索。将种群中除最优个体以外的其他个体进行适应度排序,将部分适应度较好的个体看作探狼,并在其邻域内进行随机搜索。为了提高种群多样性,防止种群陷入局部最优解,本文对次优种群的步长没有作具体规定,每段编码中随机找一段编码,将这段编码位置进行随机调换。如图7 所示,位置编码为[5 7 3 8 4 2 9 6 1],执行游走行为时,随机选择的片段为[7 3 8 4 2],随机排序后的片段为[2 8 3 4 7],则随机游走后的位置编码为[5 2 8 3 4 7 9 6 1],利用随机游走方式增加了种群多样性。
(3)召唤机制。首先,随机选择某一机器上所有工件并找出这段编码,如图8 所示,头狼个体编码为[5 7 3 8 4 2 9 6 1],猛狼个体编码为[4 1 3 8 6 7 5 9 2],随机选择的并行机为2;其次,选择剩余个体与最优个体的编码片段对应位置进行交叉,并且剩余位置编码用部分映射交叉,对应编码位置在第4 位,将这段编码与猛狼个体编码相应位置进行部分映射交叉,交叉调整后的猛狼个体编码为[5 1 3 8 4 2 9 6 7],将新的编码进行译码计算出适应度,若调整后的适应度优于原编码适应度,则将原编码进行替换。这种交叉方式能够保留在某一台并行机所选择的加工工件,从而保留了较优的排序片段。

Fig.7 Wandering schematic图7 游走示意图
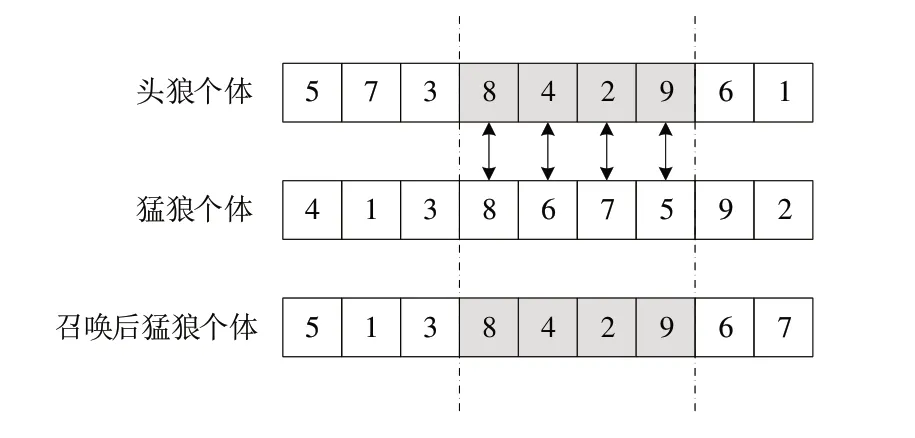
Fig.8 Calling schematic图8 召唤示意图
(4)围攻机制。将最优个体编码与次优个体编码进行比较,相同位置的编码将保留,如图9 所示,最优个体编码为[5 7 3 8 4 2 9 6 1],其他个体的编码为[6 7 3 4 8 2 9 5 1],比较后发现编码7、3、2、9、1 是相同位置相同编码,这些编码不发生变化,其他位置编码采用随机方式重新进行编码。围攻时的位置已经接近本次迭代最优位置,采用随机方式进行邻域搜索,增加解的多样性,有利于跳出局部最优解。
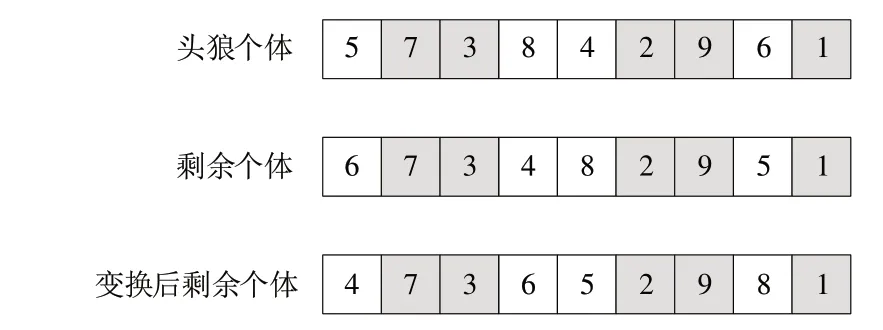
Fig.9 Besieging schematic图9 围攻示意图
3 实验设计仿真建模与分析
3.1 仿真建模
针对本文所提出算法,先用一个标准算例验证算法有效性,然后通过遗传算法和混合果蝇算法对不同规模算例进行仿真实验,验证其优越性。利用Plant Simulation 软件建模仿真分析、Simtalk2.0 语言进行编程,建立优化算法模型如图10所示。
3.2 算法参数设置
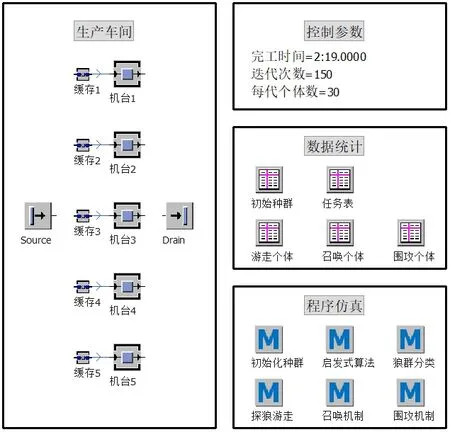
Fig.10 Modeling of 5 parallel machine scheduling for 30 workpieces图10 30工件5台并行机建模
启发式狼群算法主要参数有:工件数N,并行机机器数M,迭代次数D以及每迭代一次保留的个体数即种群规模G,各参数取值如表1 所示。根据算法主要参数找到L16(45)正交表设计正交实验如表2所示。

Table 1 HWPA parameters and values of each level表1 HWPA参数及各水平取值

Table 2 Orthogonal table and fitness value of HWAP parameters表2 HWPA参数正交表及适应度值
通过正交实验结果如表3 所示,绘制相应参数对算法影响水平趋势图,如图11所示。
比较各参数对所求结果适应度的影响。通过图11 可以看出,工件数目越少,适应度越好,并行机数目越多,适应度越好,算法迭代次数在150 时最好,狼群规模在30 左右能达到最优。根据正交实验结论设计实验参数D=150,G=30。
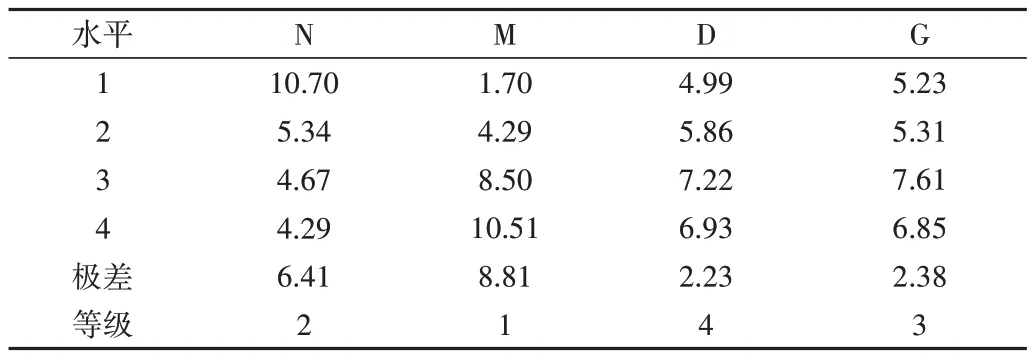
Table 3 Average fitness values of HWPA parameters表3 HWPA各参数平均适应度值
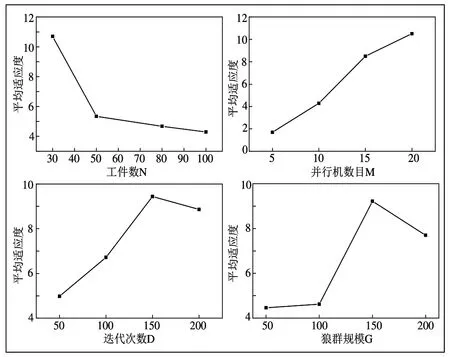
Fig.11 Trend of influence level of each factor on algorithm图11 各因素对算法影响水平趋势
3.3 有效性验证
本文用一个已知实例[15]验证启发式狼群算法有效性,仿真中的初始化参数为:D=150,G=30,探狼规模为种群规模的50%。利用软件仿真建模,编写算法程序,进行50 次仿真,求取仿真平均值,得到最优结果甘特图如图12所示。
仿真实验得出的最小化最大加工时间为7,与文献中结果相同,证明本文提出的启发式狼群算法有效。
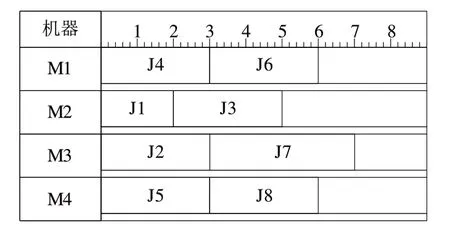
Fig.12 Gantt chart of optimal solution of 8×4-problem图12 8×4问题最优解甘特图
3.4 不同规模实验比较
为了多方位验证算法有效性,设计不同规模的实验与遗传算法和混合果蝇优化算法进行比较。实验数据来自文献[16]。通过查阅文献[17-20]设置参数如下:N={30,50,80,100,120},M={5,10},每组规模进行20 次实验,每个实例迭代次数150 次,每一代的种群规模数为30,遗传算法交叉概率0.9,变异概率0.1,混合果蝇算法的种群规模和最大迭代次数与其他算法一致,果蝇搜索半径为[-5,5]随机数,启发式狼群算法探狼数量为种群数量的50%。每组规模的实验结果如表4所示。
表4 中,IR1 表示目标函数值较GA 改进百分比,IR2 表示目标函数值较FOA 改进百分比。不同规模问题每一次迭代后的最小化最大完工时间点线图如图13所示。

Table 4 Test results of different scale problems表4 不同规模问题测试结果
3.5 实验结果分析
通过实验比较可以看出,启发式狼群算法相比其他两种算法能得到较优结果,由于对初始种群进行了改进,启发式算法为每个工件选择了加工时间最短的机器,并通过改变最大完工时间机器上的工件分配,从而使该HWPA 在迭代初期就能表现出其优势。在GA 与FOA 搜索过程中,若增加迭代次数最终也能搜索到与HWPA 接近的结果,但搜索效率会降低。在150 次迭代搜索范围内,不同规模算例实验结果显示,HWPA 的目标值较GA 平均改进了107.35%,较FOA 平均改进了113.62%,精度提升较高,即使问题规模改变,启发式狼群算法也能够使计算结果达到相对最优值,具有较好的鲁棒性。通过对智能行为机制的改进,使得每一次迭代后的最优解中保留了较优的工件分配片段。同时,采用随机分配方式进行调整,增加了跳出局部最优解的可能,进一步使最终寻优结果达到较为满意的程度。
从点线图中可以看出,小规模不相关并行机调度中最小化最大完工时间相差不大,随着工件数量与机器数目增多,3 种算法在150 次迭代后完工时间差值增大,在并行机数目保持不变的情况下,工件数目越多,启发式狼群算法的优势也越明显,说明启发式狼群算法对解决以最小化最大完工时间为目标的大规模不相关并行机调度有其优势。
4 结语
本文针对不相关并行机调度问题,提出一种启发式狼群算法,通过启发式算法改变部分初始种群的选择方式,同时根据该问题特点,对狼群算法智能行为机制重新进行设计。通过仿真优化实验证明该算法有效,同时设置不同规模算例实验,在一定迭代次数内,本文所提算法能有效优化最大完工时间,且求解问题规模越大优化效果也越明显,为不相关并行机调度问题研究提供了一定参考价值。未来将继续研究该算法在多目标并行机调度问题中的应用。
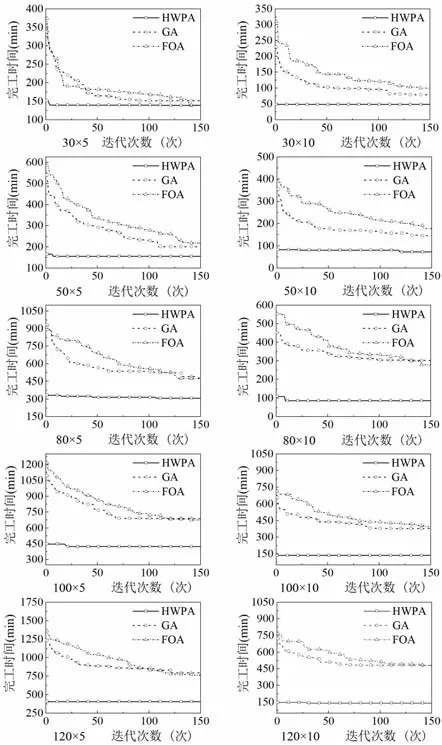
Fig.13 Optimal solutions of different scales图13 不同规模最优解

