基于CEEMD-SA-RNN的柴油机曲轴轴承磨损预测

李英顺，田宇，左洋，张国莹，周通

(北京石油化工学院信息工程学院，北京 102617)

步兵战车是供步兵机动作战用的装甲战斗车辆，具有高机动性。步兵战车经常在恶劣的环境下工作，为保障车辆的正常运行，定期对机械进行故障检测是必要的防患措施。传统的零部件故障检测方法需要对一些部件进行拆解，在消耗人力物力的同时，对检测者的要求也很高。而利用计算机通信技术进行机械故障检测具有无需拆解、高效等优点，相较于传统的检测方法更好，成为了国内外学者研究的焦点。

Y. Chen等[1]利用快速傅里叶变换(Fast Fourier transform，FFT)对振动信号进行分析和处理，但其特征具有易聚集特性，不能很好地识别，需要人为介入；张玲玲等[2]采用小波包-AR谱对变速器轴承故障进行特征提取，但该方法有小波基的选取困难缺陷；J. Cheng等[3]利用经验模态分解(Empirical Mode Decomposition， EMD)对振动信号进行分解，但EMD会出现模态混淆现象；W. Xia等[4]利用自适应小波和集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)处理信号，用故障树分析喷油提前角度的大小，但由于实际运算有限，不能很好地消除已添加的白噪声的影响，会引起重构误差，而补充的集合经验模态分解方法(Complementary Ensemble Empirical Mode Decomposition，CEEMD)，可以很好地消除白噪声对信号的影响；周小麟等[5]使用补充的集合经验模态分解、缎蓝园丁鸟优化算法和最小二乘支持向量回归(Least Squares Support Vector Regression，LSSVT)实现超短期风电功率组合预测，但此算法的拟合精度和采样点数成正比，需要较多数据，而循环神经网络(Recurrent Neural Network，RNN)可有效避免此类问题。

柴油机曲轴轴承的振动信号采集相对困难，很容易混入噪声。本研究对原始数据进行软阈值处理，使用多种分解方法对已处理的数据进行分解，分析各项指标，通过奇异值分解方法对数据进行特征提取，并作为神经网络模块的特征集。循环神经网络适用于多分类问题，适合对曲轴轴承的磨损程度进行预测。此外，利用模拟退火算法找寻循环神经网络的最优参数，能有效提高系统的预测准确率。

1 算法设计

1.1 信号处理算法

1.1.1 补充的集合经验模态分解

补充的集合经验模态分解是基于集合经验模态分解(EEMD)的想法，向信号中添加相反白噪声，实现抵消其影响的新分解方法[6-8]。具体步骤如下。

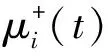
(1)

(2)

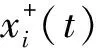
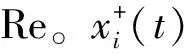
(3)

(4)

式中：imfj为最终得到的第j个本征模态函数；r为分解后的余项分量。利用已得到的本征模态函数进行自回归模型分析，可以观测系统的特征和工作状态[9]，在故障诊断和预测中应用广泛。其定义为

(5)

式中：c为常数项；εt为平均值是0、标准差是σ的随机误差，σ值恒不变。

1.1.2 奇异值分解

奇异值分解(Singular Value Decom-position，SVD)是根据矩阵的固有特性对矩阵进行分解的常用方法。其计算步骤如下：

设矩阵E(e×g)的秩为r′，则存在矩阵U和W及对角阵D，使得[10]

E=UDWT。

(6)

式(6)成立，则式(6)为E(e×g)的奇异值分解，其中:

U(e×e)=[u1,u2,…ue],

(7)

(8)

Δr′×r′=diag(σ1,σ2,…σr′),

(9)

Wg×g=[w1,w2,…wg],

(10)

r′=min(e,g)。

(11)

1.2 故障预测算法

1.2.1 循环神经网络

曲轴轴承磨损程度需要细致划分，循环神经网络(RNN)不仅可以处理任意长度的输入，还适用于多输出问题。因此使用RNN作为预测的基本网络，其结构见图1。

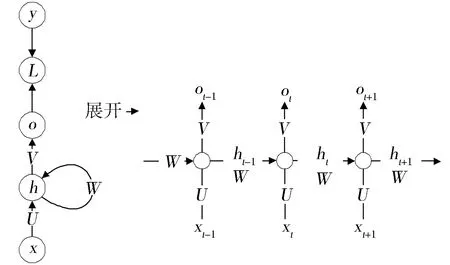
图1 RNN结构

图1中x为输入，h为隐层单元，o为输出，L为损失函数，y为训练集的标签[11-12]。

ht=f(U·xt+W·ht-1+b)，

(12)

ot=V·ht+c，

(13)

yt=g(ot)。

(14)

式中：f()和g()为激活函数。在RNN的训练调参过程中，需要调优参数只有V，W，U3个参数。V，W，U的偏导求解和所有历史时刻的数据有关。各偏导为

(15)

(16)

(17)

(18)

(19)

1.2.2 模拟退火算法

20世纪80年代，Kirkpatrick等提出了模拟退火算法[13-14](Simulated Annealing，SA)，该算法来源于晶体冷却过程，是一种概率算法。SA原理[15]如下：从某一高温开始，利用参数控制温度下降，结合概率的突跳性，寻找全局最优解。该算法具有时变特性，可以有效避免陷入局部极小问题。

算法步骤如下。

1) 初始化：起始温度T0(足够高)，初始解S(迭代开始)，迭代次数L，终止温度T1；

2) 设k=1，2，…L，做第3至第6步计算；

3) 产生新解S′；

4) 计算增量ΔC=f(S′)-f(S)，f()为目标函数；

6) 若满足迭代次数则继续，否则转第3步；

7) 看是否满足目标温度，若不满足则T逐渐减小，且T>T1，然后转第3步。

2 模型建立

系统模型由两部分组成：第一部分是补充的集合经验模态分解与奇异值分解方法相结合(CEEMD-SVD)的信号处理模块；第二部分是模拟退火算法优化循环神经网络(SA-RNN)的故障预测模块。建立的系统模型主体框架见图2。

图2 模型主体框架

2.1 信号处理模型

信号处理流程见图3。磨损导致轴承游隙增大，运行精度降低，振动噪声增大。采用连续加速的方法对曲轴轴承进行诊断，故障时的振动特征相比正常情况更加明显，因此利用此方法提取振动信号作为依据对部件进行故障分类。

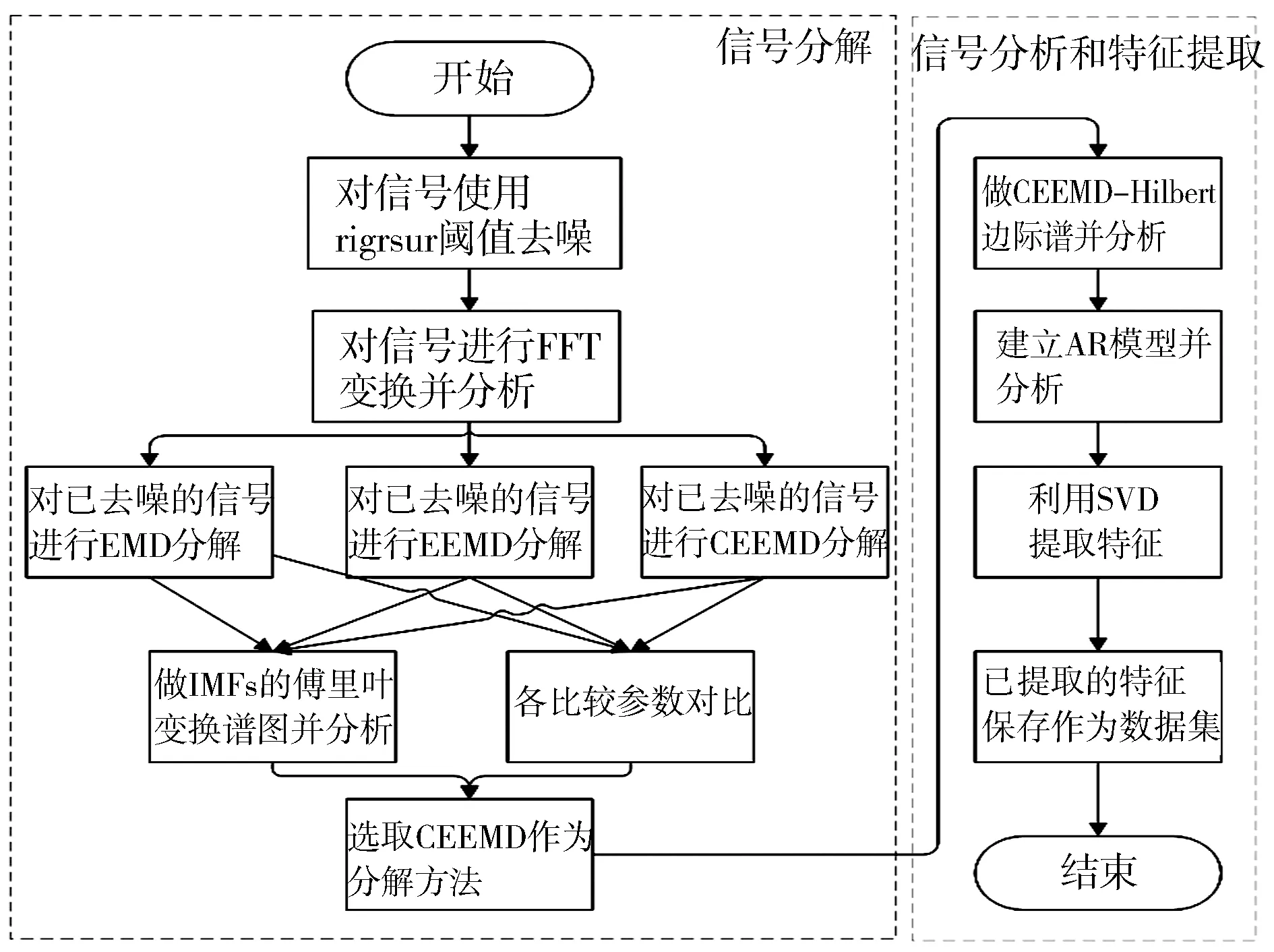
图3 信号处理流程

对已采集的信号进行软阈值处理。分别使用无偏似然估计(rigrsure)、最优预测变量阈值(heursure)、广义阈值(sqtwolog)和最小最大阈值(minimaxi)4种方法对信号进行处理。以结构相似性(Structural Similarity,SSIM)作为衡量去噪效果的指标，通过结果对比选择rigrsur阈值法对原始信号进行处理。对已处理的信号，使用经验模态分解、集合经验模态分解和补充的集合经验模态分解进行分解，通过对比得出4项参数指标，选取补充的集合经验模态分解方法作为最优信号分解方法。对信号进行CEEMD分解后，使用自回归模型对各工况下前6个IMF分量谱图及累加能量谱图进行对比分析。观察到从第7个IMF分量开始，其能量占总能量之比很低，因此选取前6分量作为初始向量矩阵，并对其进行奇异值分解，得到的特征分量作为神经网络的特征集。

2.2 网络预测模型

建立循环神经网络模对信号进行预测，使用模拟退火优化循环神经网络可以更好地预测曲轴轴承的磨损程度。

模型步骤如下：

1) 初始化参数，随机产生隐含层节点数和序列个数(小于隐含层节点数)，进行循环神经网络预测，得出准确率；

2) 更新隐含层节点数和序列个数为随机值，且序列个数小于隐含层节点数，利用两参数创建新的循环神经网络，并进行预测，得出新网络的准确率；

3) 比较新旧准确率的大小，若新值大则接收并存储新值，否则以概率接受新状态(Metropolis准则)；

4) 看是否满足迭代次数，若不满足则转第2步；

5) 看是否满足目标温度，若不满足则T逐渐减小，然后转第2步；满足则得出最优解并结束。

模拟退火算法优化的循环神经网络步骤见图4。

图4 SA-RNN步骤

3 试验验证

以某步兵战车柴油机第4道曲轴轴承为研究对象。选用PCB601A01型ICP工业加速度传感器，将其放置于油底与缸体结合处3缸左右位置，通过加装强力磁座吸合于测试部位表面。定义轴承游隙0.05～0.11 mm为正常工况，0.11～0.15 mm为轻度磨损，0.15～0.20 mm为中度磨损,0.20 mm以上为重度磨损。采集转速1 800 r/min正常工况、轻微磨损、中度磨损和严重磨损下的曲轴轴承振动信号，传感器的采样频率为12.8 kHz，在运行平稳后，每次采样16 384个点作为一条数据。使用该数据，分别利用CEEMD-SVD算法和SA-RNN算法进行故障预测分析。

3.1 CEEMD-SVD试验

考虑现场采集原因，本研究首先对原始信号进行小波阈值去噪处理，因为硬阈值会引起吉布斯效应，所以选择软阈值处理。使用无偏似然估计、最优预测变量阈值、广义阈值、最小最大阈值，并使用SSIM作为衡量去噪效果的指标。正常信号使用不同阈值方法去噪结果见图5。

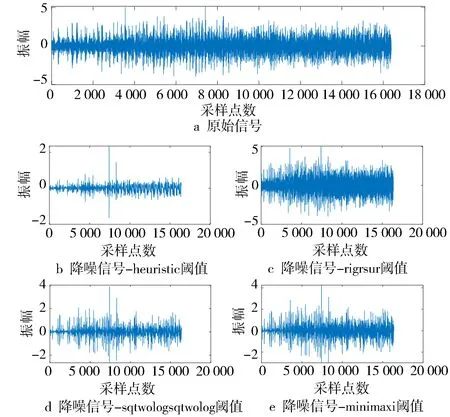
图5 正常信号使用不同阈值方法去噪结果

由表1中SSIM值可以看出，使用无偏似然估计法去噪效果最好。

表1 不同阈值方法得到的SSIM值

对已处理的信号进行傅里叶变换，得到的结果见图6。

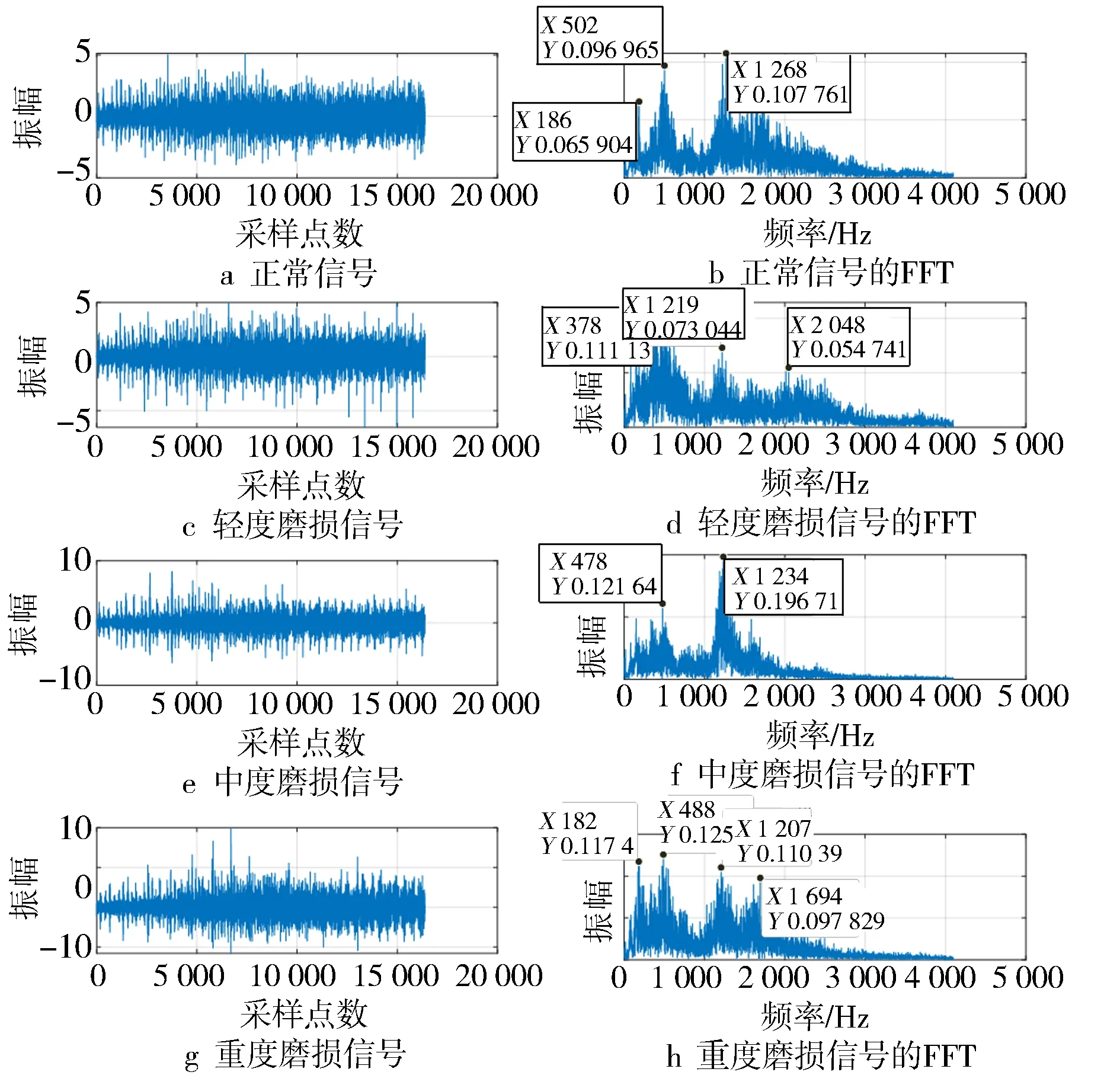
图6 各工况下的FFT结果

由图6可知，经过傅里叶变换后的正常工况信号有3个明显峰值，分别在185 Hz，500 Hz和1 270 Hz左右；轻微磨损下的信号有3个明显峰值，分别在380 Hz，1 220 Hz和2 050 Hz左右；中度磨损下的信号有2个明显峰值，分别出现在480 Hz和1 235 Hz附近；严重磨损信号有4个明显峰值，分别出现在185 Hz，490 Hz，1 200 Hz和1 700 Hz附近。

对已去噪的信号，分别使用EMD、EEMD(0.210 0)、CEEMD(0.110 0)方法进行分解并比较。比较参数有均方误差、正交性、分量个数和时间(见表2)。

表2 正常去噪信号分解方法比较

由表2可得出，最优分解方法为CEEMD分解，EMD和EEMD算法存在一定的模态混淆现象，从结果可以看出，EEMD在多次尝试改变初始参数后均方误差及正交性的参数值依然较大，运行时间也比EMD长。造成该问题的原因可能是在有限次的运行过程中无法消除白噪声的影响，致使重构误差较大，完备性差。CEEMD算法经过多次改变参数后得到的均方误差及正交性都优于EMD算法，后续采用CEEMD算法作为系统模型的信号处理方法。

进行CEEMD分解，得到10个IMF分量及余项r。信号CEEMD的能量谱见图7。

图7 能量谱(CEEMD)

由能量谱可得出，从第7个分量开始能量很低。采用前6个分量作为主要研究对象，对前6个IMFs进行傅里叶变换，其频谱图见图8。

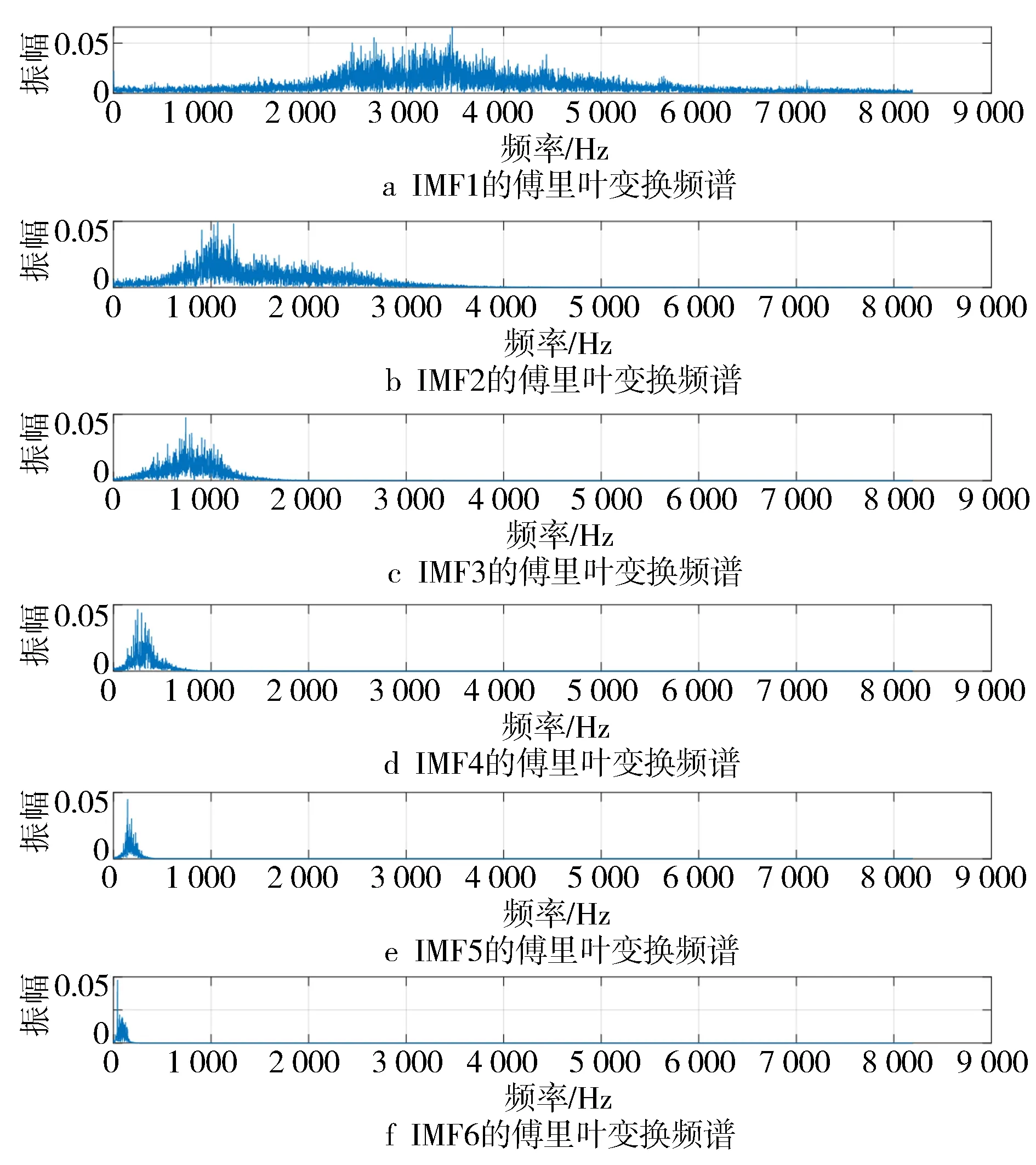
图8 CEEMD-IMF1～6的傅里叶变换频谱

作为类比，本研究也使用了EMD及EEMD方法得到相应的傅里叶变换频谱图(见图9和图10)。

图9 EMD-IMFs1～6的傅里叶变换频谱

由图8至图10对比发现，前6个分量的频率范围有明显的区分度， CEEMD方法下的混叠现象更小，再次证明针对曲轴轴承的振动信号CEEMD方法更加适用。

图10 EEMD-IMFs1～7的傅里叶变换频谱

对正常工况进行CEEMD分解并作出Hilbert边际谱(见图11)。

图11 CEEMD-Hilbert边际谱

由图11可见，Hilbert边际谱中3个峰值和之前FFT变换下的峰值相近，在180 Hz，500 Hz及1 300 Hz左右。

各工况的前6个分量的CEEMD-AR谱对比见图12，各工况下前6个IMF分量CEEMD-AR谱累加能量对比见图13。

图12 正常与3种磨损情况下的前6个分量CEEMD-AR谱对比

图13 各工况下前6个IMF分量CEEMD-AR谱累加能量对比

对图12、图13进行分析可得以下结论。

1) CEEMD-AR谱的功率表幅值能量主要集中在6 500 Hz以内。

2) 从分量信号图中可以看出，能量由正常、轻微磨损、中度磨损和重度磨损依次递增的特征频带有IMF1分量3 850 Hz以内，IMF2分量1 450 Hz以内，IMF3分量875 Hz以内，IMF4分量450 Hz以内，IMF5分量250 Hz以内，IMF6分量100 Hz以内。曲轴轴承轻微磨损和中度磨损递增的特征频带有IMF1分量4 850～5 550 Hz。

3) 从累加能量对比图可以看出，正常磨损能量递增为75 Hz以内，轻微磨损能量递增为50 Hz以内，中度磨损能量递增为75 Hz以内，重度磨损能量递增范围为50 Hz以内。

使用SVD对信号进行特征提取，考虑能量占比，使用前6个分量作为柴油机曲轴轴承磨损程度的特征，并作为深度学习的数据集。利用CEEMD-SVD方法提取的柴油机曲轴轴承磨损故障特征的数据集(部分)见表3。

表3 训练数据与测试数据(部分)

3.2 SA-RNN试验

使用RNN对数据进行训练及预测，参数设置如下：迭代次数2 000，批次大小1，学习率0.01 ，输入6，输出1，序列长度4，隐含层10。得到120个测试集的预测结果(见图14)。

图14 测试集预测值与实际值对比

预测值的准确率为92.307 7%，虽然得到的准确率大于90%，但并不满足大于95%的条件。本研究尝试使用模拟退火算法对循环神经网络进行优化，设置隐含层节点数和序列长度为可变参数x1和x2，准确率y作为模拟退火算法的目标函数。约束条件为隐含层节点数小于等于10，并求准确率的最大值、最优隐含层节点数和序列长度。设置初始温度为100，截止温度9，链长10，降温速率0.9。通过迭代，得到每次温度下降链长中的最优解(见表4)。

表4 SA-RNN调参及准确率

SA-RNN退火效果见图15。由图15可见，使用模拟退火算法优化的循环神经网络在每次降温时准确率上升速度很快，准确率在达到95%后逐渐趋于稳定，这充分说明该算法的效率较高、稳定性良好。最后得到最优隐含层节点数为8，序列长度为2，准确率为97.479%，相比未进行优化的准确率为92.307 7%的RNN，优化效果明显，其误差也在可接受范围内。综上可见，使用模拟退火算法进行优化可以降低局限性，更好获得全局最优解，同时具有良好的鲁棒性、稳定性，这说明该系统具有可行性。

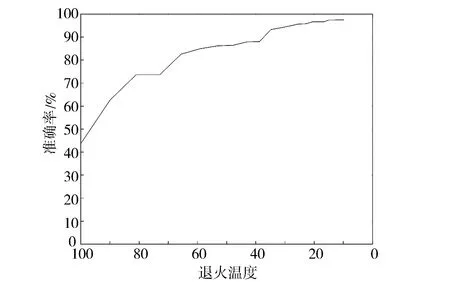
图15 SA-RNN退火效果

4 结束语

利用柴油机曲轴轴承振动信号来预测判断轴承的磨损程度，提出了一种补充的集合经验模态分解与奇异值分解相结合提取信号特征，使用模拟退火算法优化循环神经网络对故障进行预测的方法，建立了CEEMD-SA-RNN模型。利用柴油机曲轴轴承振动信号对提出的算法进行了试验验证，结果表明CEEMD在对曲轴轴承振动信号分解方面更加适用，使用模拟退火算法的循环神经网络相比常规循环神经网络，得到的准确率提高了5%以上。