电杆复合横担极限承载力及截面参数影响分析★

王 哲，朱永凯，杨岚琦，郑春生，江文强

(1.胜利石油管理局有限公司电力分公司，山东 东营 257000; 2.华北电力大学机械工程系，河北 保定 071003)

0 引言

配电网呈蛛网结构，节点多、延伸广，鲜有专用的线路走廊[1]。相比于输电线路，配电线路的绝缘配置水平较低，雷击导致的故障数量明显高于输电线路[2]，尤其在沿海地区的盐雾环境中，更易发生闪络事故[3]。传统配电线路中常用的木杆、水泥杆、钢管杆、铁塔在长期运行中存在着易开裂、耐腐蚀性差等缺点[4-5]，对输电线路的安全运行造成严重威胁。玻璃纤维增强树脂基复合材料(GFRP)具有轻质高强、耐腐蚀、绝缘性好等钢材无可比拟的优点，是其理想的替代材料[6-9]，已广泛应用于航空航天、汽车制造以及电气工业等诸多领域[10]。采用复合绝缘横担替代传统配电线路铁横担，是降低配电网雷击跳闸率的有效措施，可以减小杆塔尺寸、降低线路造价、提升输送功率[11-14]。近年来，我国多位学者对复合横担展开研究。文献[15]针对配电用矩形复合横担的电气性能进行试验研究，验证了复合横担相比于传统横担具有更好的绝缘性能。文献[16]对复合横担覆冰断线的动力响应进行分析，考虑复杂运营荷载下的动力效应和长期使用的耐久性得到复合横担上的危险位置。同样有许多学者利用具体工程案例，通过试验的方法对高压输电线路用复合横担的承载、变形能力进行分析，为我国复合杆塔结构的设计与应用提供技术参考[17-18]。不过，针对10 kV配网线路用复合横担的力学特性还缺乏研究。

本文对配网电杆用复合横担在极限工况下的力学特性进行分析，研究复合横担在极限工况载荷作用下的破坏过程，分析截面参数对极限承载力的影响，从改变横担截面参数的角度提出复合横担的优化方案，提高复合横担的承载能力。

1 复合材料横担建模

1.1 复合材料横担有限元建模

本文所研究横担整体长度为1 900 mm，宽、高均为75 mm，壁厚为7 mm。绝缘子孔与跳线孔位置均在横担纵向，孔径为21.5 mm；抱箍孔位于横担沿导线方向，孔径为19.5 mm。电杆、横担模型如图1,图2所示，尺寸如表1所示。

表1 复合横担尺寸

复合横担为轴对称图形，对模型进行简化，选取1/2试件进行求解。由于横担端部封口对承载力影响较小，在建模时将其忽略。按表1尺寸要求在相应位置分别创建绝缘子孔、跳线孔以及抱箍孔。复合横担有限元模型见图3。

1.2 材料参数设置及复合材料铺层

复合材料生产方式为玻璃纤维整体挤压而成，因此用单层玻璃纤维的材料属性作为横担整体的材料属性，层厚为横担壁厚。在弹性材料行为中弹性类型选择单层板，复合材料堆叠方向即法向轴方向为壁厚方向，主轴方向为横担长度方向。

由于损伤准则的需要，设置所要求的材料参数，具体材料属性参数如表2所示。Hashin损伤准则将材料的破坏分为纤维拉伸、压缩破坏，基体拉伸、压缩破坏四种形式，其表述形式如下。

(1)

(2)

表2 玻璃纤维材料力学性能

(3)

(4)

其中，σ11,σ22分别为材料两个主方向应力；σ12为面内剪切应力；XT,XC分别为纵向拉伸、压缩强度；YT,YC分别为横向拉伸、压缩强度；SL,SY分别为纵向、横向剪切强度；α决定剪应力对于纤维拉伸损伤准则影响，介于0和1之间。

蔡-吴准则表达形式如下：

Fiσi+Fijσiσj+Fijkσiσjσk=1

(5)

蔡-希尔准则表达形式如下：

(6)

最大应力准则表达形式如下：

(7)

1.3 网格划分及边界条件

单元类型为SC8R，指派网格为扫掠网格，扫掠路径均沿厚度方向，单元总数为10 078。复合模担网格划分见图4。

将抱箍孔设置为铰接约束(U1=U2=U3=0)，在对称面处设置对称约束(U3=UR1=UR3=0)。载荷通过一参考点施加(见图5)。参考点位于绝缘子孔中心的正上方，将参考点与两绝缘子孔建立耦合约束。对参考点施加沿Y轴、Z轴方向的载荷即可对横担施加垂直荷载与横向水平荷载(见图6)。

1.4 施加极限工况荷载

由损伤准则可以判断试件是否发生损伤，横担刚好发生损伤时横担作用在参考点上的反作用力即为横担的极限承载力。通过参考点对横担施加一个很大的位移直至横担被破坏，再输出参考点上的位移与反作用力数据，得到位移与反作用力曲线，由各损伤准则可以判定横担发生损伤的分析步，最终在曲线中获得损伤发生时的反作用力，即可得到横担的极限承载力。创建场输出，MSTRS对应最大应力准则TSAIH对应蔡-希尔准则，TSAIW对应蔡-吴准则，HSNMTCRT对应基体拉伸损伤，HSNMCCRT对应基体压缩损伤，HSNFTCRT对应纤拉伸损伤，HSNFCCRT对应纤维压缩损伤，上述7个变量输出中任一值达到1即代表该准则判据下横担发生损伤。

2 极限工况仿真结果分析

通过参考点对横担施加30 mm竖直方向位移，即U2=-30 mm。损坏位置如图7所示,由Hashin准则中的HSNMTCRT值可以得知，横担在绝缘子孔周围出现了基体拉伸损伤。

由图8(a)可知，横担上表面靠近抱箍处存在较大的沿纤维方向的应力分布，但由于该处纤维组织完好，沿纤维方向拉伸强度高，并没有出现损伤；而抱箍孔局部应力较大，由于纤维组织的完整性被破坏，出现了损伤。由图8(b)可知，横担在绝缘子孔处存在较大的垂直纤维方向的应力分布，复合材料横向的强度主要由基体提供，因此由Hashin损伤准则判定此处发生了基体拉伸破坏。最终得到横担极限承载力如表3所示。根据极限承载力反算出横担承载不同导线型号时的覆冰厚度，结果如表4所示。

表3 复合横担极限承载力 N

表4 极限覆冰厚度

3 复合横担结构参数影响分析

复合材料横担的加固从改变截面形状的思路出发。首先改变横担的截面形状，分别计算不同截面横担的极限承载力，得到极限承载力最高的横担截面形状。在最佳截面形状的基础上，尽可能减小壁厚以节约材料，针对横担发生破坏位置优化载荷施加方式。

3.1 不同截面形状的极限承载力对比

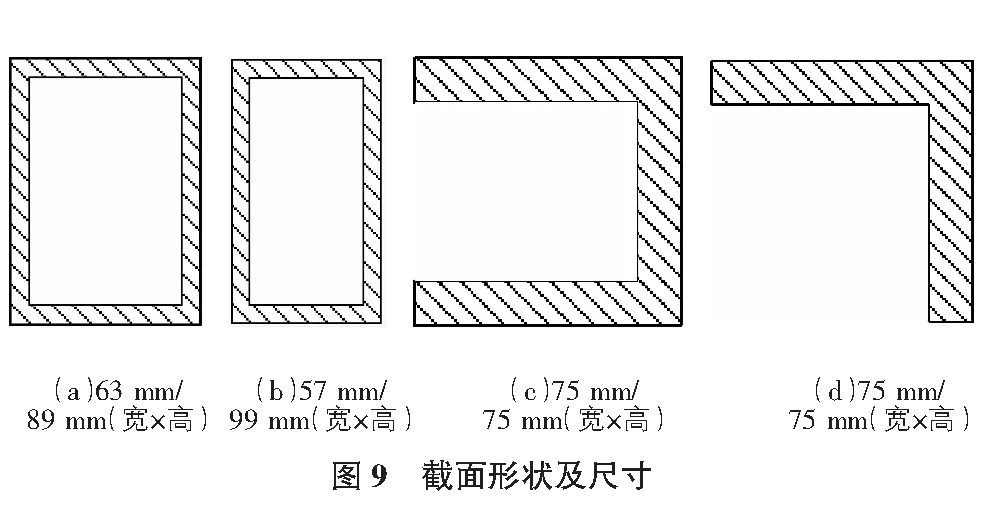
按照前文所述极限承载力的获得方法，分别对四种横担施加位移载荷，根据损伤准则判断最终获得横担的极限承载力。各截面形状复合横担破坏时应力云图如图10所示。复合横担发生破坏时对应的极限承载力列于表5中，其中比例因子为各截面复合横担与原截面极限承载力的比值。

表5 横担极限承载力

3.2 截面厚度及载荷施加方式影响分析

3.2.1 截面厚度对极限承载力影响

从减小壁厚出发优化复合横担，以期用更少的材料达到较好的承载能力，因此针对1号截面横担作减少壁厚的处理，分别计算5 mm,3 mm壁厚时横担的极限承载力，结果如表6所示。

表6 1号截面横担极限承载力

由表6可知，壁厚对横担承载力的影响是十分显著的。以原截面横担极限承载力为基准，当复合横担壁厚从7 mm减小至5 mm，极限承载力降低了36%；壁厚减小到3 mm时，复合横担极限承载力降低80%。因此，对于复合横担壁厚的优化应当是谨慎的。通过图12垂直纤维方向应力云图也可以看出，绝缘子孔处有较大的垂直纤维方向的应力分布，最大应力值为47.28 MPa，显然超出了材料垂直纤维方向的拉伸强度，因此发生破坏。

3.2.2 优化载荷施加方式

由于原截面与优化后的截面均存在此问题，显然不是单纯改进截面形状能够解决的。为模拟现实中绝缘子对横担的作用，将施加荷载的参考点与两绝缘子孔面进行耦合，这造成了作用在绝缘子孔处局部的荷载过大，超出了材料所能承载的极限。因此考虑改进绝缘子对横担的作用形式，在绝缘子孔与绝缘子之间添加垫片，令荷载能够均匀地施加在绝缘子孔周围的一片区域内，避免局部荷载过大使横担发生损伤。添加垫片的处理对应到软件仿真当中，处理为改变参考点与横担耦合的区域。

如图13所示，在绝缘子孔周围划分出边长为横担宽的矩形，矩形中心为绝缘子孔圆心，将参考点与该矩形区域耦合以模拟垫片的作用效果。在改进载荷施加方式后，横担的极限承载力如表7所示。

表7 优化荷载施加方式后横担极限承载力

优化荷载施加方式后，由图14应力云图表明，绝缘子孔周围的应力相较于原载荷施加方式有了很大幅度的降低，但是应力值在横担对称面处较大，较薄的壁厚使横担对称面处的承载能力下降，需在对称面处使用较厚的壁厚以保证横担的承载力。

分别以5 mm壁厚时横担和原截面横担的极限承载力为基准。由表7数据可知，优化载荷施加方式后，横担的极限承载力提高16%，不过优化后横担极限承载力与原截面横担的相比仍有24%的差距，需要进一步对横担进行优化。

3.2.3 变截面复合横担

表8 优化形状与荷载施加方式后的横担极限承载力

以原截面横担的极限承载力为基准。在优化横担形状与荷载施加方式后，横担的极限承载力有了大幅度的提高，极限承载力提升了41%，横担材料的使用减少了12%，兼顾了提升性能与节省成本。

4 结论