基于专家PID的带臂四旋翼无人机控制方法

陈宝，周祖鹏，卫欢，吕延钊，睢志成

（桂林电子科技大学机电工程学院，广西桂林 541004）

0 引言

近年来，随着科学技术的发展，导航和控制技术不断成熟，飞行机器人不断应用于航空拍摄、灾难现场勘查、环境建模［1］及抓捕罪犯。一种具有作业能力的带臂无人机（Unmanned Aerial Vehicle，UAV）成为了新的研究热点［2］，带机械臂的四旋翼无人机主要由四旋翼无人机和机械臂组成，并具有与环境交互的能力，通过与环境的“接触式”应用，带臂无人机具有广泛的应用前景，如危险目标的抓取、飞行目标物的捕获及抓取物品运送到指定地点等。

面向潜在的应用，国内外研究机构设计出多种飞行机械臂系统，德雷塞尔大学实验室将四旋翼无人机配备机械臂并对机械臂进行动力学建模，以及搭建了测试平台［3］。文献［4］设计了一种应用于林冠采样的航空机械手，用于解决在森林冠层复杂环境中的样本采集，并借助回路中的运动捕捉以补偿惯性传感器的不足，使无人机和机械臂的移动抓取更加精准；文献［5］提出了一种解决空中操纵器碰撞问题的方法，该方法能够在空中操纵器碰撞期间和碰撞后保持稳定；文献［6］介绍了一种大工作空间并联航空机械手的设计，该机械手能够在侧面以及空中机器人下方进行物理交互，以实现空中机械臂的无奇异工作空间和高灵巧度；文献［7］设计了一种带机械臂无人直升机控制系统，由无人直升机和机械臂组成，并使机械臂拔出固定在地面上的直杆；文献［8］介绍了四旋翼无人机和单自由度机械臂组成的飞行机械臂控制系统，并使机械臂能够抓取静止目标；文献［9］利用一种单自由度抓手或绳索实现目标物体的空中运输；文献［10］介绍了机械臂直升机系统的建模和分析，并设计了一种线性二次规划控制器（Linear Quadratic Regulator，LQR），同时对系统闭环性能进行仿真实验；文献［11］针对带臂飞行器飞行过程中的动态稳定性，提出了一种组合控制法，将增益调度跟模型参考自适应控制（Model Reference Adaptive Control，MRAC）有机融合；文献［12］设计了一种带臂无人机的控制器，实现其稳定飞行，该控制器采用基于反馈线性化和双积分器相结合进行控制；文献［13］设计了自适应鲁棒阻抗控制器；文献［14］为飞行机械臂系统设计了模型预测控制器，面向末端执行器的轨迹进行跟踪控制；文献［15］建立了漂浮在空间中刚体之间接触的运动方程，对于非合作目标的抓取，引入了阻抗控制，当机械臂与被动目标碰撞时，通过阻抗控制匹配的方法进行有效的调节。

本文针对带二自由度的机械臂无人机控制系统进行设计，利用拉格朗日-欧拉方程对二自由度机械臂的运动学和动力学特性进行全状态建模，并通过设计专家PID 控制器对带臂无人机进行稳定性控制，且与常规的PID 控制器进行对比。通过Matlab/Simulink 对带臂无人机进行仿真，以验证带臂无人机在位置控制和姿态控制及二自由度机械臂在受干扰下的运动稳定情况，其实物如图1 所示。

图1 带臂四旋翼无人机系统Fig.1 System of quadrotor UAV with manipulator

1 带臂无人机系统模型

1.1 带臂无人机运动学模型

带臂无人机控制系统主要是机械臂与无人机以铰接方式进行连接的。通过拉格朗日-欧拉方程分析系统的内部运动关系，从机械臂末端的位姿及受力方式向前计算得到机械臂在无人机上的受力情况，进而分析无人机的位姿，简易模型［16］如图2 所示。

由图2 模型坐标系可推导该系统的运动模型。其中：Σb表示机载坐标系；Σe表示机械臂末端坐标系；ΣI表示大地坐标系；Pb=[x y z]T∈R3和Θb=[φ θ ψ]T∈R3表示无人机在惯性框架中的位置和欧拉角，φ是绕Xb轴的滚转角（roll），θ是绕Yb轴的俯仰角（pitch），ψ是绕Zb轴的偏航角（yaw）；Q=[q1q2]T表示机械臂关节角度。所有的广义矢量的坐标变量可表示为L=[PTΘTQT]T∈R8×1。

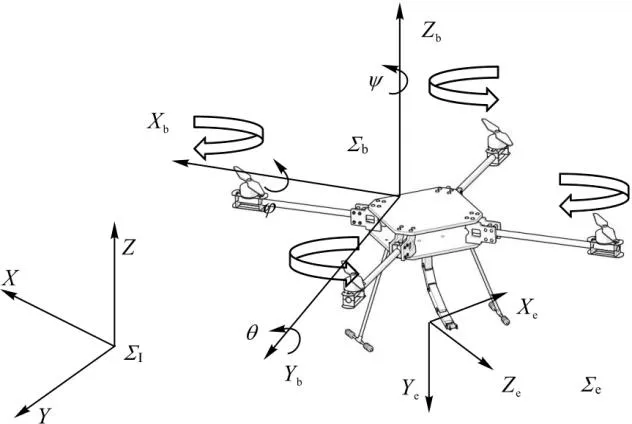
图2 带臂无人机的坐标系模型Fig.2 Coordinate system model of UAV with manipulator

本文的运动学是旋翼平台在惯性坐标系I 下的位姿变换以及机械臂的坐标系E 在惯性系统下位置与姿态方面的表达。而坐标系B 与大地坐标系I 之间的旋转变换矩阵为Rb。

1.2 带臂无人机动力学模型

带臂无人机通过四个升力Fi(i=1，2，3，4)提升无人机并抓取作业，机械臂的交互使无人机的位姿发生改变，即无人机与机械臂形成整个控制系统。对带臂无人机动力学建模是根据机械臂角度和无人机位置及偏航角得出带臂无人机的力矩，并通过动力学的逆问题得出带臂无人机的实际位姿及角度。

带臂无人机动力学模型是通过拉格朗日-欧拉动力学方程分析系统内部的关系与运动情况。主要通过拉格朗日-欧拉方程［16-17］进行计算，拉格朗日-欧拉方程表达式为：

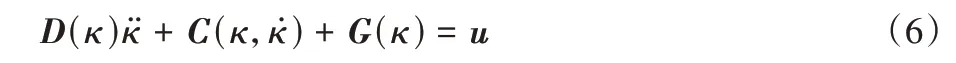
其中：κ=[x z θ q1q2]T；u主要由无人机在X和Z方向的力矩uf和无人机力矩uλ及机械臂力矩uτ组成；D是惯性矩阵，D∈R5×5；C是离心力和哥氏力构成的矩阵，C∈R5×1；G是重力项构成的矩阵，G∈R5×1。D、C、G表示无人机的X和Z方向的位置和俯仰角及机械臂通过拉格朗日-欧拉方程编写的动力学结合矩阵。Y方向由无人机的总推力和总质量得到，偏航角及滚转角取决于力矩和转动惯量。

而带臂四旋翼无人机在运动过程中四个旋翼会产生升力和旋转力矩，关系可表示为：

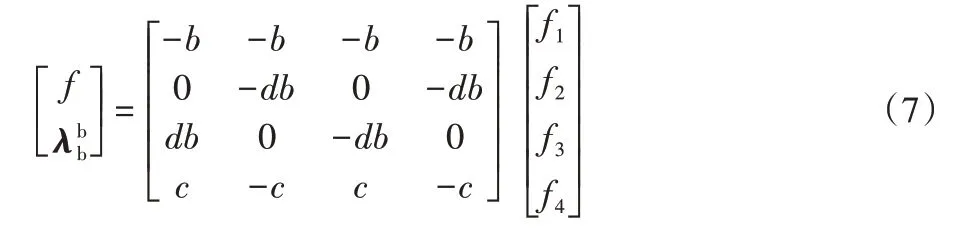
为了实现对带臂无人机的闭环控制需对带臂四旋翼无人机动力学进行正逆运算，正动力学主要是为了计算出无人机位姿[x z θ]及二自由度机械臂的两个转角qi(i=1，2)。则方程为：

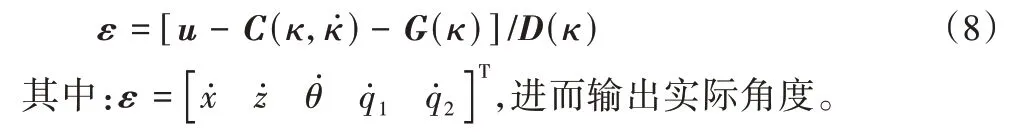
2 专家PID控制器设计

专家PID 控制主要利用受控对象和控制规律的知识进行控制，对被控制的对象不需要精确的模型，使用专家经验对系统模型进行设计控制。对于系统模型的控制专家PID具有灵活性、适应性和鲁棒性，可根据系统的工作状态及误差情况灵活地选择相应的控制规律去控制，并根据专家知识和经验，能动性地调整控制器的参数，适应对象特性及环境的变化，通过利用专家规则，控制系统模型在非线性、大偏差下可靠地工作，使带臂旋翼无人机在专家PID 控制律下能够可靠地使旋翼无人机稳定飞行及平稳地抓取物品。

专家PID 主要由五个控制律组成［18］，通过工作状态及误差去选择相应的控制律去稳定数据，并对参数进行调节达到对控制系统稳定的作用。控制结构如图3 所示。

图3 带臂无人机的控制系统结构Fig.3 Structure of control system of UAV with manipulator

专家PID 控制算法如下：

对期望值和实际值进行误差分析，令e(k)表示当前的误差值，e(k-1)、e(k-2)分别表示前一个和前两个采样的时刻误差，表达式分别为：

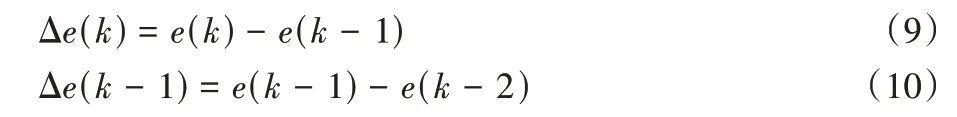
设计专家控制规律，根据误差及其变化进行定性分析，控制规律如下。

1）当|e(k)|＞M1时：误差绝对值很大，应按控制器的输出最大（或最小）形式输出，以达到调整误差的作用，使误差的最大速度绝对值减小，可以达到快速使系统控制稳定的作用。其控制器输出为：

其中：c表示系数。

2）当e(k)Δe(k) ＞0 时：

①如|e(k)|≥M2，应按控制器较大的输出进行控制，以使绝对值的误差往减小的方向变化，达到控制的目的。其控制输出为：

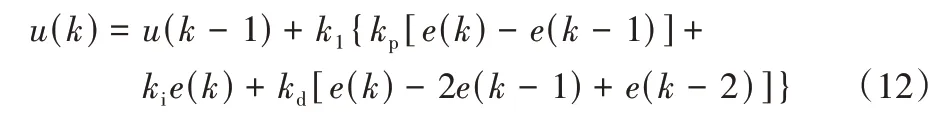
②如|e(k)|＜M2，表示误差往大的方向变化但误差绝对值变化不明显，可使用一般控制。其控制器输出为：

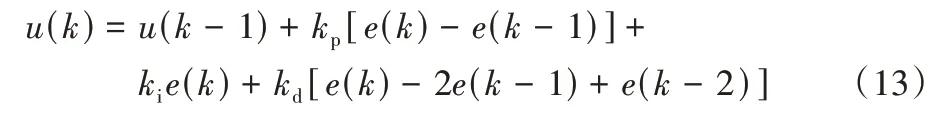
3）当e(k)Δe(k) ＜0，Δe(k)Δe(k-1) ＞0 且e(k)=0 时，表示误差值不是很大，或处于平衡状态，其控制器输出可保持不变，输出为：

其中：u(k)表示在上一次输出过程中输出值很小，可利用上次的输出值作为这一次的输出。

4）当e(k)Δe(k) ＜0 且Δe(k)Δe(k-1) ＜0 时：

①如|e(k)|≥M2时，表示误差较大处于极限状态，应使控制器输出较大，达到控制的目的。其控制器输出为：

②如|e(k)|＜M2时，表示误差比较小，可使控制器输出较小，其控制器输出为：

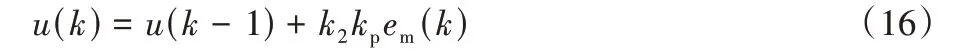
5）当|e(k)|≤ε时，表示误差的绝对值很小，应加入积分作为控制输出，以减小稳态误差。控制器输出为：

其中：a、b是系数；em(k)为误差e的第k个绝对值；u(k)为第k次控制器的输出；u(k-1)为第k-1 次控制器的输出；k1为增益放大系数，k1＞1；k2为抑制系数，0 ＜k2＜1；M1、M2为误差界限，M1＞M2＞0；k为周期序数；ε为任意小的正实数。通过对带臂无人机进行控制器设计，专家PID 能够很好地对无人机进行稳定控制，具有很好的鲁棒性。

3 轨迹规划

机械臂的轨迹规划主要以点到点的运动方式进行，即规划一条从初始位置q(t0)到最终位置q(tf)的轨迹，机械臂的轨迹有利于抓取物品的流畅性及规律性。本文采用五次多项式进行轨迹规划，在t0初始时刻和tf最终时刻的角度、角速度、角加速度满足如下：

五次多项式为：

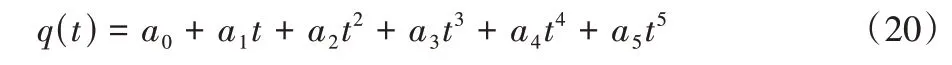
其中：t=tf-t0；ai(i=0，1，2，3，4，5)为系数。

根据初始位置和最终位置的角度、角速度和角加速度可得方程为：

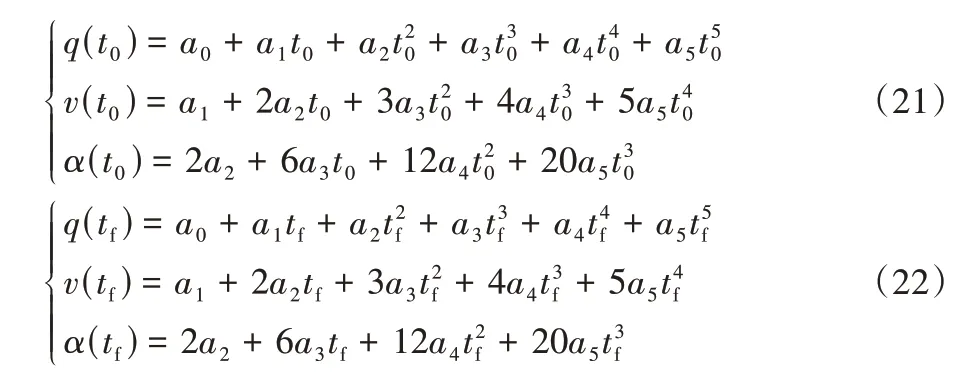
通过方程组（21）～（22）可得ai(i=0，1，2，3，4，5)系数，即机械臂关节期望的角度、角速度和角加速度可为：

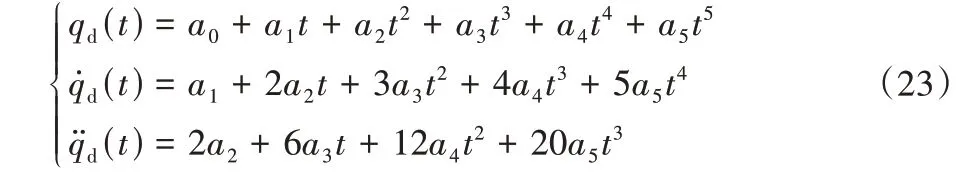
根据式（23）可对带臂无人机的机械臂进行轨迹规划。

4 仿真实验

为了验证在专家PID 控制下带臂四旋翼无人机的稳定性和优越性，使用Matlab/Simulink 对带臂无人机在仿真环境下进行实验，带臂无人机在扰动的情况下仍然处于稳定，以验证算法的可行性。

经实际测量可知，带臂四旋翼无人机系统的各项参数和指标［19］如表1 所示。

表1 带臂四旋翼无人机系统仿真参数Tab.1 Simulation parameters of quadrotor UAV system with manipulator

表1 中：Ct和Cq分别是推力系数和扭矩系数；mv是无人机的质量；mi(i=1，2)分别是基座和各关节的质量；d是转子到无人机中心的距离；H是无人机中心到地面的距离；Li(i=1，2)分别表示机械臂的臂长；Ixx、Iyy、Izz分别是无人机的转动惯量。

对带机械臂无人机的位置和姿态进行仿真，以验证算法的可行性和稳定性，在仿真之前设置专家PID 控制器的数值，采样时间ts=0.001，误差界限M1=0.8，M2=0.000 5，增益放大系数K1=20，抑制系数K2=0.6，任意小的正实数ε=0.000 1，系数a=0.5，b=0.01，c=0.2 等参数，则带机械臂无人机在设计参数的专家PID 控制器下的仿真性能如图4～10 所示。

从图4 表示的带臂无人机在专家PID 和常规PID 控制器下位置对比曲线可以看出：X方向专家PID 的收敛速度很快在t=5 s 时就已经达到稳定而且超调量很小，而常规PID 在t=22 s 时才达到稳定，超调量要更大一些；Y方向专家PID 在t=4.5 s 达到稳定，常规PID 在t=30.5 s 达到稳定；Z方向专家PID 在t=5.0 s 达到稳定，常规PID 在t=19.0 s 达到稳定。相较于常规PID，专家PID 收敛更快、稳定性更好。图5 表示带臂旋翼无人机在偏航角ψ方面的控制，带臂无人机以π/6 的角度偏航，专家PID 控制器在t=0.9 s 时就达到稳定，而常规PID 在t=5.7 s 才达到稳定。图6 表示带臂无人机二自由度机械臂关节角度对比曲线，专家PID 对机械臂的控制比常规PID 控制更好，机械臂关节收敛性更好、超调量更小。

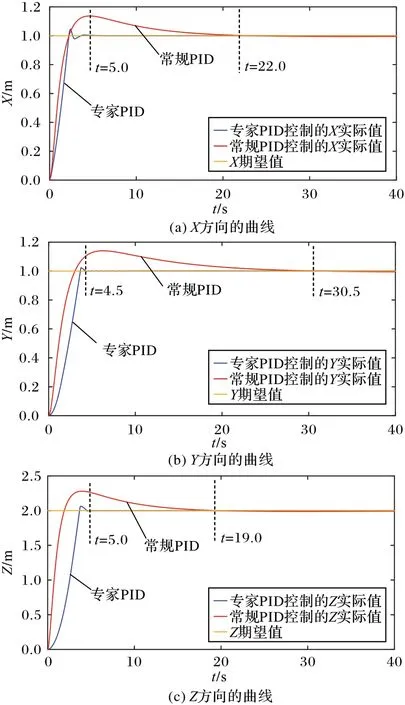
图4 位置对比曲线Fig.4 Curve comparison of position

图5 偏航角ψ对比曲线Fig.5 Curve comparison of yaw angle ψ

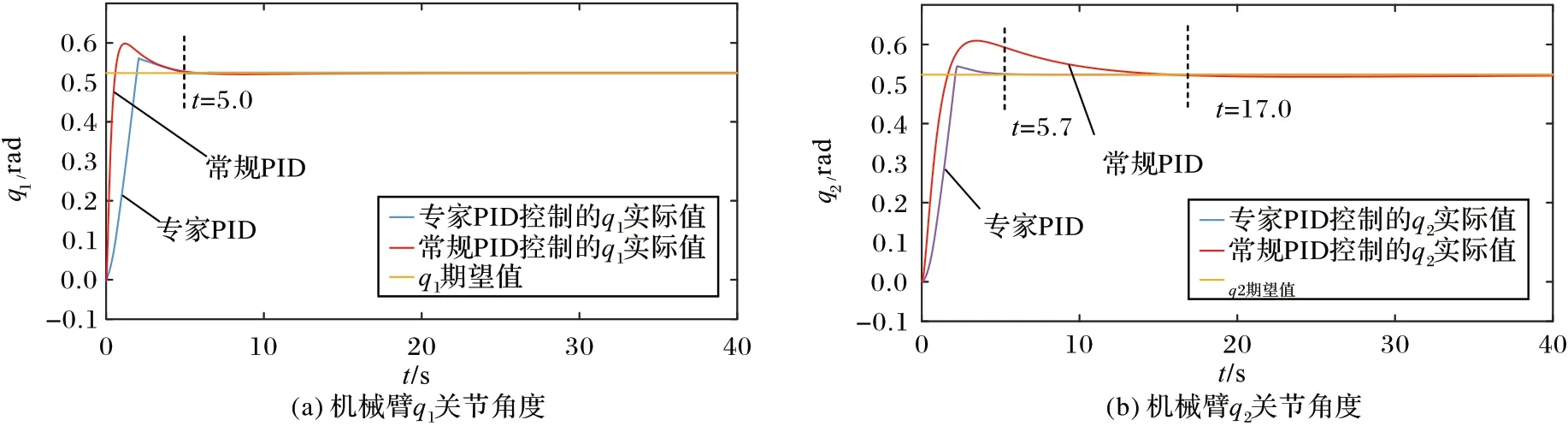
图6 机械臂关节角度对比曲线Fig.6 Curve comparison of joint angles of manipulator

为了验证专家PID 对扰动的抑制效果，使用阶跃信号和正弦波信号分别模拟平均风和阵风的扰动。平均风表示风速不随时间而变化的风，阵风表示风速随时间而变化的风，其风速有突发的特性。用于描述在两种风的干扰下，带臂无人机的稳定性及收敛性。以偏航角ψ为例，在t=2 s 至t=6 s 的阶跃信号为w(t)=1(2 ＜t＜6)；在t=4 s 至t=24 s的正弦波信号为w(t)=0.6sin[π(t-t1)/2] (4 ＜t＜24)，其中：t1为起始时间，t为干扰时间。设偏航角ψd=0 rad 表示悬停效果，实验结果如图7 所示。

图7（a）为阶跃信号扰动下两种控制器估计的结果，可以看出，在t=2 s 有突发扰动，而在扰动开始时专家PID 虽然有一点超调，但影响较小，且很快收敛到真实值，并保持稳定；当t=6 s 扰动消失时专家PID 快速恢复到稳定值。对于常规PID，当出现扰动时超调比较大持续时间长，扰动消失时不能快速收敛到稳定值。图7（b）为正弦波信号扰动下两种控制器估计对比曲线，可以看出，t=4 s 时有扰动，而在扰动时专家PID 对真实扰动的跟随性及准确性都比较好，偏差性较小；在t=24 s 扰动消失时虽然有一点超调但影响比较小，而常规PID 相对于真实扰动有一定的偏差，且扰动消失时超调比较大。

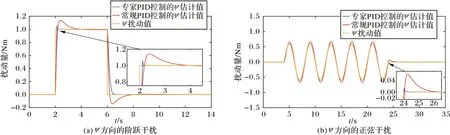
图7 外力干扰对比曲线Fig.7 Curve comparison of external interference

由图8 所示的带臂无人机在两个控制器控制下轨迹曲线对比可知：专家PID 控制的带臂无人机开始起飞后就快速地到达了期望的目标轨迹，离期望的目标轨迹偏差比较小，最终能到达目标位置；而常规PID 控制的带臂无人机开始起飞后需要飞一段时间才慢慢地接近期望目标轨迹，且离期望的目标轨迹有很大的偏差，不能到达最终的目标位置。即专家PID 优于常规PID，收敛性更好。

图8 带臂无人机轨迹曲线对比Fig.8 Comparison of trajectory curves of UAV with manipulator

而在实际的应用中，可以通过分层控制分别控制无人机和机械臂，上层控制无人机，下层控制机械臂，无人机带动机械臂到达指定位置，通过机械臂的运动执行任务，即机械臂在五次多项式轨迹规划下稳定到达指定位置。设关节1 和关节2 的初始角度q1和q2分别为0，目标位置角度分别为π/6和π/4。机械臂关节角度如图9 所示。

图9 机械臂角度轨迹曲线对比Fig.9 Curve comparison of manipulator angle trajectories

由图9 机械臂角度轨迹曲线知，带臂无人机的机械臂在五次多项式规划下到达指定位置，且在专家PID 控制下机械臂的轨迹跟随比常规PID 更好，跟踪误差较小。由图10 机械臂角速度可知，机械臂第1 个关节的初始角速度为0，然后速度慢慢增大到最高点，并在第5 秒时达到了最大值为0.098 rad/s，最后角速度逐渐减小到0；机械臂第2 个关节的初始角速度为0，然后慢慢增大到最高点，并在第5 秒时达到了最大值为0.147 rad/s，最后角速度逐渐减小到0。可以看出机械臂在专家PID 的控制下，关节角速度平稳地从0 到最大值再逐渐减小到0，显示了机械臂能够快速平稳地到达指定位置并执行任务。

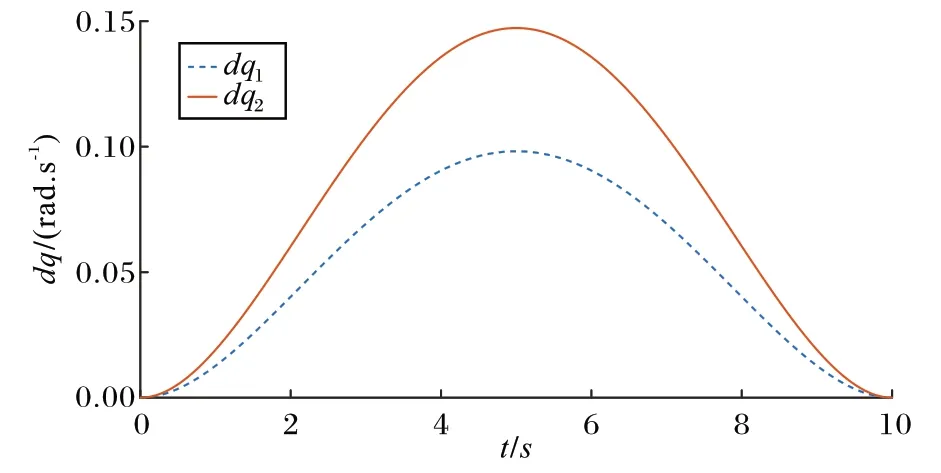
图10 机械臂角速度Fig.10 Manipulator angular velocity

5 结语

本文对二自由度的带臂无人机系统全状态的运动学和动力学模型进行探讨，并在此基础上对带臂无人机控制系统进行设计及算法研究，分析带臂无人机的运动状态稳定性，并提出了利用专家PID 控制器智能整定带臂无人机的稳定参数，与常规PID 进行对比，专家PID 收敛速度更快、稳定性更好、超调量更小，大幅提高了带臂无人机的位姿跟踪效果，使带臂无人机在抓取物品时能更精准操作。仿真结果表明带臂旋翼无人机在专家PID 的控制下有更好的抗扰性和鲁棒性，改善性能更好，具有很好的优越性和全局稳定性，有很好的实用价值。