考虑订单扰动因素的热轧重调度分布估计算法

王一荻，李志伟，张文新*，李铁克，王柏琳

（1.北京科技大学经济管理学院，北京 100083；2.钢铁生产制造执行系统技术教育部工程研究中心（北京科技大学），北京 100083；3.宁波钢铁有限公司，浙江宁波 315807）

0 引言

板坯的热轧生产阶段指将板坯加热后经粗轧和精轧机组进行轧制加工，热轧工艺复杂导致其生产调度结果直接影响订单交货期、生产效益和效率等。热轧批量调度是热轧生产阶段的重要内容，用于确定板坯在热轧工序的分组和排序，不仅考虑板坯间的工艺约束，同时还考虑与其他工序的衔接问题［1］。因此，研究热轧批量调度问题对于加速钢铁企业技术的发展有重要的理论基础和现实意义。

热轧批量调度是一类典型的NP 难问题，一直受到众多国内外学者的研究和关注。文献［1］将板坯热轧批量调度问题抽象为板坯分配和排序两个子问题，并针对这两个部分设计了指派启发式和排序启发式算法；文献［2］将热轧批量调度问题归结为带软时间窗的车辆路径问题，运用约束满足技术进行求解；文献［3］针对热轧批量调度问题，建立带钢分配和排序两阶段问题模型，设计两阶段启发式规则对该模型求解；文献［4］针对热轧批量调度问题采用改进的两阶段人工蜂群算法进行求解；文献［5］针对板坯批量调度问题，在优化目标中额外引入了出炉温度跳跃惩罚，基于单亲遗传算法对问题进行求解；文献［6］将热轧批量计划归结为车辆路径问题，并在计划数不确定的情况下求解；文献［7］将无缝钢管热轧批量调度问题归结为依赖顺序安装时间的流水车间调度问题，采用分支定界法和两阶段启发式算法分别求解不同规模的调度问题；文献［8］针对无缝钢管热轧批量调度问题，在建立模型时考虑了配送地址等因素，并设计了聚类算法和混合变邻域算法对模型进行求解；文献［9］研究了热轧圆钢的批量调度问题，提出了基于规则的变邻域搜索算法进行求解。

上述文献针对静态环境下的热轧批量调度问题难以适用于当今热轧生产工序，在实际的热轧生产过程中存在许多动态扰动，紧急订单插入、机器故障等不确定性因素导致初始调度方案无法继续执行，因此需要提高钢铁企业应对突发扰动的能力以确保生产过程的连续稳定。文献［10］针对钢厂热轧生产调度中出现板坯延迟交货、未达到质量标准和机器故障等扰动因素，提出了基于约束满足的优化方法，设计了变量和值序启发式算法；文献［11］针对加热炉-热轧区间板坯的生产调度问题，考虑加热炉或热轧机故障等扰动因素建立重调度模型，运用非支配排序遗传算法对该问题进行求解；文献［12］针对热轧板坯动态调度问题，分析了生产过程的扰动因素，并提出了人机交互的热轧动态调度系统解决该问题。可以看出，目前对热轧重调度研究成果较少；此外，热轧生产通常被抽象为单机环境，而单机重调度目前取得了一些研究成果［13-17］，但由于热轧生产的特殊工艺要求，无法直接应用于热轧重调度问题。

实际钢铁企业中，经常出现随机到达的紧急订单，对这类扰动事件的快速高效响应是生产连续和质量稳定的重要保障，也是提升客户满意度的关键手段。本文针对紧急订单插入这类扰动因素，提出基于事件驱动的热轧生产重调度策略，并以最小化订单拖期惩罚和板坯跳跃惩罚加权和为目标，建立热轧重调度模型，结合问题特征，设计了基于插入位置的整数编码方案和概率模型的分布估计算法（Evolution of Distribution Algorithm，EDA），最后运用实际生产数据验证模型和算法的有效性。

1 问题描述与策略分析

1.1 热轧批量调度与紧急订单插入

在编制热轧批量计划时，计划人员根据产品的工艺规范要求对销售订单进行选择并分解成生产订单（以下简称订单），生产车间根据订单将板坯按照交货期和轧制宽度、硬度、厚度等工艺规程进行组批构成若干轧制单元，进而排序形成热轧批量调度如图1 所示，开始生产。在热轧生产过程中，每个轧制单元生产后需要留出安装时间更换轧辊，因此热轧批量调度问题可视为一类考虑安装时间和热轧工艺约束的单机批量调度问题。

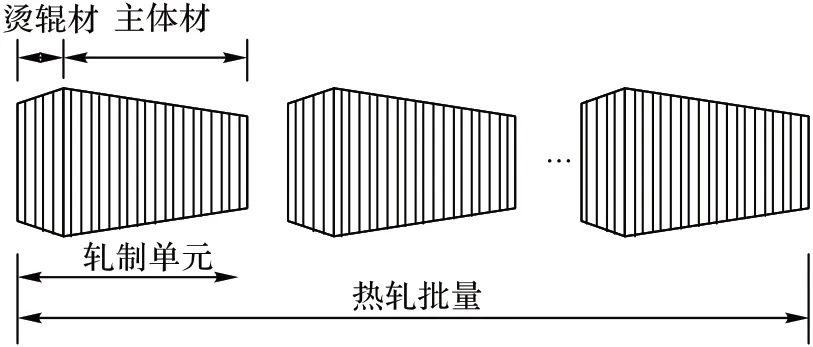
图1 热轧批量调度示意图Fig.1 Schematic diagram of hot rolling batch scheduling

相较于一般单机调度问题，热轧生产工艺复杂。一个轧制单元内的板坯是由烫辊材和主体材两部分组成的，其中主体材部分是生产的主要阶段且数量较多，单纯依靠人工编排耗时长且很难取得较优结果，因此本文仅考虑主体材部分的轧制工艺规程。为保证产品质量、生产效益且减少对轧辊磨损的影响，在一个轧制单元内的板坯需要按照轧制规程有序排列，使主体材满足以下轧制规程：

1）轧制宽度应尽可能递减变化，变化要平滑；若轧制宽度反跳时，跳跃差不能超过150 mm；如遇到同宽板坯连续轧制，则要求有一定的长度限制。

2）轧制厚度最好向非减的方向变化，变化要平滑。

3）轧制硬度变化平滑且呈现递增或递减的变化，禁止反复跳跃。

4）轧制单元内的宽度、厚度、硬度禁止同时跳跃。

5）当轧制宽度、硬度和厚度相互冲突时，优先级为硬度、厚度、宽度。

6）轧制单元的总轧制长度有一定限制。

在热轧生产过程中，经常出现紧急订单插入等突发情况，静态调度模型难以应对热轧生产的突发扰动情况。紧急订单作为一类典型的生产扰动因素，其热轧重调度是实际生产中亟待解决的难题，对该问题的研究在理论和实践方面均具有重要意义。特别针对紧急订单交货时长短的情况，只有将订单中的板坯插入至当前调度方案中才能保证按期交货的要求。订单拖期不但会使企业产生拖期生产成本，降低车间生产效率，更影响了客户满意度，进而影响企业效益。从客户角度来说，订单的拖期惩罚越大，客户满意度越低，因此本文将最小化拖期惩罚作为一个优化目标。此外，热轧生产有成批生产和连续性强的特点，生产工艺要求极为严格，以节约产能，保证产品质量和生产节奏。从生产工艺的角度来说，板坯的跳跃惩罚越小，产品质量越稳定，且生产效率越高，因此本文将最小化相邻板坯跳跃惩罚设为另一优化目标。

综上所述，考虑订单扰动的热轧重调度问题可以描述为：在t=0 时刻，热轧车间按照初始计划组织生产；在t=T时刻，有若干块紧急板坯到达，所有板坯的宽度、硬度、厚度、钢种、重量等属性均已知，要求在满足轧制长度限制、轧制规程、安装时间等热轧生产约束和客户订单要求的前提下，确定新板坯的插入位置并生成重调度方案，使相邻板坯总跳跃惩罚和订单拖期惩罚的加权和最小。

1.2 订单扰动下的重调度策略

本文采用基于事件驱动的重调度策略，即以新板坯的到达作为驱动重调度的事件。在新板坯到达时，根据各轧制单元的加工状态确定重调度对象，从而实时更新重调度的开始时间。重调度的对象为新到达板坯和初始调度中尚未加工的板坯。设新板坯在t=T时刻到达并需要插入到初始调度中，此时初始调度方案的状态分为尚未轧制、正在轧制和轧制完成的轧制单元，假设重调度的开始时间为t1，Pm和Cm分别为轧制单元m的加工时间和完工时间，cti为板坯i的完工时间，s为轧制单元间更换轧辊的安装时间。

1）尚未轧制的轧制单元：若轧制单元m在t=T时刻还未开始轧制，即Cm-Pm≥T，则该轧制单元进行重调度，重调度的开始时间为t1=Cm-Pm。

2）正在加工的轧制单元：若轧制单元m在t=T时刻正在加工，即Cm≥T且Cm-Pm＜T，则尚未轧制的轧制单元进行重调度，重调度的开始时间为t1=cti。

3）轧制完成的轧制单元：若轧制单元m在t=T时刻已经轧制完成，即Cm＜T，则对应轧制单元不再进行重调度，重调度的开始时间为t1=Cm+s。

基于上述热轧板坯的加工状态、重调度加工对象及开始时间进行重调度，重调度策略流程如图2 所示。订单扰动发生前，根据已有热轧批量计划执行初始生产调度方案。当紧急订单到达时，则需重新确定板坯的加工信息，以进行重调度并生成最新调度方案。

图2 热轧重调度策略流程Fig.2 Flowchart of hot rolling rescheduling strategy

2 考虑订单扰动的热轧重调度模型

2.1 符号定义

为了便于模型的描述和建立，定义符号和变量如下：

1）索引与集合。

n为初始板坯数量，n′-n为新板坯数量，I为所有轧制板坯编号的集合，包括初始板坯和新板坯，I=｛0，1，…，n，…，n′｝；

i为轧制板坯编号，其中i=0 为构造的虚拟板坯，构造该板坯以确保同一个轧制单元内的板坯顺序能够形成闭环，即每个板坯有且仅有一个前驱和后继的板坯，i∈I；

K为轧制单元的集合，K=｛1，2，…，k｝，其中k为轧制单元总数；

m为轧制单元编号，m∈K；

Nm为轧制单元m包含轧制板坯的有序集合，Nm（v）表示轧制单元m内的第v块轧制板坯，轧制单元集合为｛N1，N2，…，Nk｝；

δi为与板坯i同宽且连续轧制的板坯集合。

2）已知参数。

wi、gi、ri和li分别为板坯i的轧制宽度、硬度、厚度和长度；

wmax、gmax和rmax分别为相邻板坯间轧制宽度、硬度和厚度变化的最大值；

Lmax为一个轧制单元的板坯总长度限制；

Qmax为一个轧制单元内连续轧制同宽板坯的长度限制；

s为轧制单元间更换轧辊的安装时间；

pti为板坯i的轧制时间；

di为板坯i的交货期，根据该板坯所属订单的交货期获得；

α为订单拖期的惩罚系数，α∈［0，1］；

M为足够大的正整数。

3）决策变量。

cti为板坯i的完工时间；

qii′为板坯i到板坯i′的跳跃总惩罚值；

、和分别为板坯i到板坯i′的宽度、硬度、厚度的跳跃惩罚值；

Pm和Cm分别为轧制单元m的加工时间和完工时间。

2.2 重调度模型

本文在文献［5］提出的热轧生产调度模型基础上，考虑紧急订单插入的扰动因素，建立重调度模型。将新到达的板坯和发生扰动时尚未轧制的板坯作为重调度对象。不失一般性，提出如下合理假设：

假设1 初始调度方案中的轧制单元及其包含板坯的轧制顺序已知且不变。

假设2 不考虑热轧机组故障等其他扰动因素。

针对订单扰动的热轧重调度问题，以相邻板坯总跳跃惩罚和订单拖期惩罚的加权和最小为目标，建立如下数学模型。

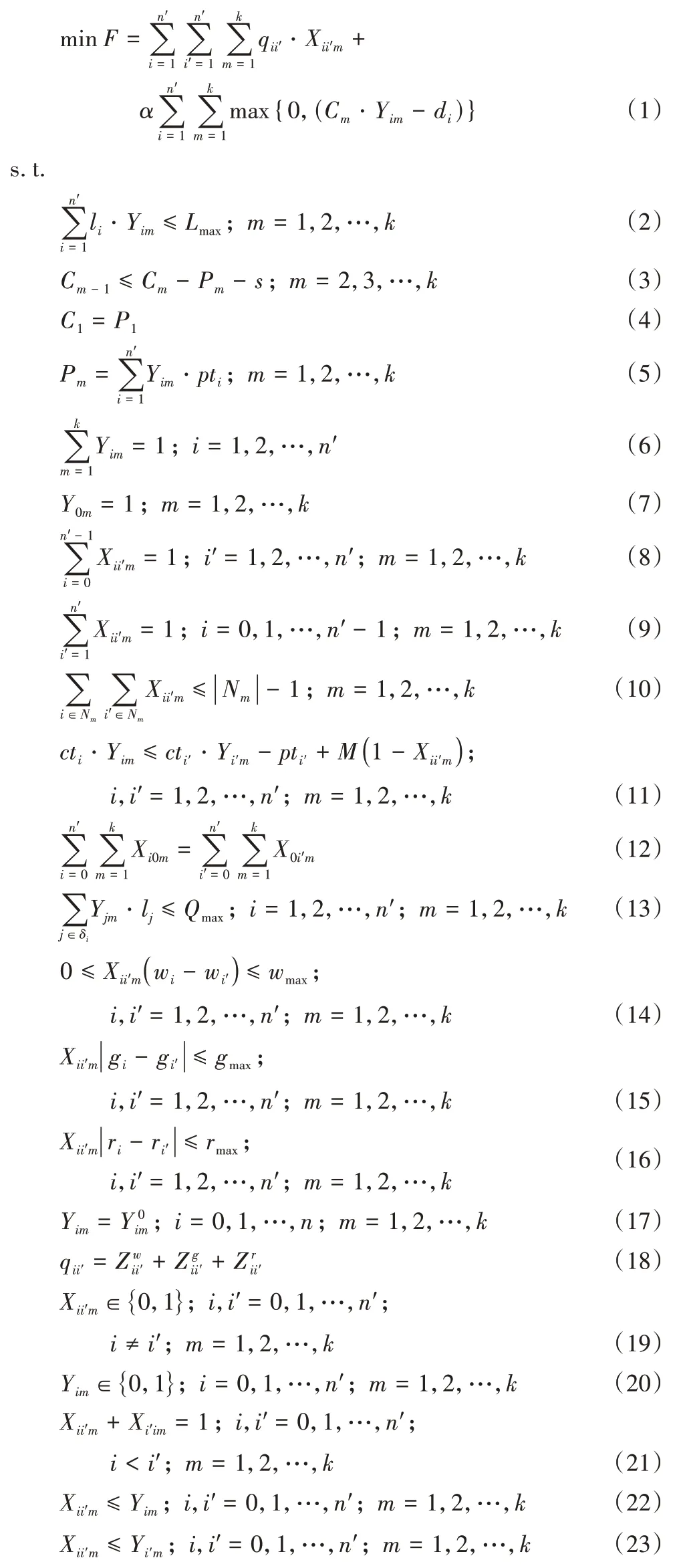
目标函数式（1）包含两层优化目标：第一层为最小化板坯间由轧制规格（宽度、硬度、厚度）变化导致的跳跃惩罚，以保证产品质量；第二层为最小化总拖期惩罚，以确保按期交货。

约束条件式（2）～（5）考虑了轧制单元的相关约束：式（2）表示轧制总长度的上限约束；式（3）表示轧制单元的先后加工顺序约束，在加工时不允许中断且需要考虑轧辊的安装时间；式（4）表示第一个轧制单元的完工时间约束；式（5）表示轧制单元和所包含板坯的加工时长关系约束。

约束条件式（6）～（16）列出了轧制单元内板坯排序约束：式（6）～（12）用于限定板坯间的顺序关系；式（13）～（16）为轧制单元生产的工艺约束，参考文献［5］构建，其中：式（6）表示一块板坯至多只能在一个轧制单元内生产；式（7）表示虚拟板坯必须被放置在每个轧制单元内，以构成回路；式（8）～（9）表示轧制单元内的板坯i前后有且仅有一块板坯；式（10）表示消除子回路；式（11）表示轧制单元内板坯的先后加工顺序约束；式（12）表示每个轧制单元内以虚拟板坯0 作为起点构成回路；式（13）表示连续轧制同宽板坯的长度上限约束；式（14）～（16）表示保证宽度、硬度、厚度平滑变化且存在跳跃上限的约束。

式（17）为重调度的特殊约束，表示初始板坯所在的轧制单元保持不变，用于保证重调度前后的计划一致性和生产稳定性。

式（18）对目标函数中的跳跃惩罚进行了定义，设定为相邻板坯跳跃的惩罚值总和。

约束条件式（19）～（23）为决策变量的取值约束。

3 重调度的分布估计算法

基于动态事件的热轧调度问题是典型NP 难问题［10］，相较于精确算法，智能优化算法可以在较短时间内获得问题解，满足实际生产需求。相较于传统的遗传算法，本文分布算法EDA 通过建立概率模型对初始种群进行采样和学习，代替了遗传算法采用的交叉、选择和变异操作［18］。概率模型的更新可以表征优良解在解空间的分布，并对概率模型进行采样生成优势群体，实现种群进化。EDA 具有较强的收敛速率和搜索能力，处理该类问题有更好的性能。本文算法EDA 的流程如图3 所示。

图3 本文算法流程Fig.3 Flowchart of the proposed algorithm

由图3 可以看出：结合本文问题特征，设计算法的关键在于编码方案、概率模型、适应度函数等方面。概率模型的建立与更新机制是决定算法有效性的关键。针对这三个方面，本文提出了基于插入位置的整数编码方案，结合模型特征提出了概率模型建立与更新方法，并定义了基于惩罚值的适应度函数。

3.1 个体编码方案

个体编码方案没有采用传统的表达板坯顺序的编码方法，而是设计了一种表示紧急订单中所有板坯插入原调度位置的编码方法，这种编码方式不仅清晰地描述了问题特征，而且缩短了编码长度，减少了繁琐的解码步骤，提高了求解效率。

个体采用整数编码形式，具体设计如下：若原调度方案中有n1块板坯，重调度t=T时刻有n2块板坯到达，等待插入至原调度方案中，定义种群中的个体编码由n2个基因位组成，表示为（x1，x2，…，xn2），其中：xj为整数，且1 ≤xj ≤i，i=1，2，…，n1。

基因xj表示第j块新板坯插入原调度中第i块板坯后的位置。若xj=xk，则按照xj和xk在个体中的先后顺序决定位置次序。根据问题模型，在每个轧制单元内引入一块虚拟板坯，包含在该调度的板坯数量中。若xk为虚拟板坯，则表示第k块新板坯插入该虚拟板坯后的位置，即插入该虚拟板坯所属轧制单元的首位。

例如，假设原调度方案中有6 个轧制单元，有40 块原调度板坯，现有5 块新板坯，个体（19，4，25，16，32）的含义为：第1 块新板坯插入到原调度方案的第19 块板坯后，第2 块新板坯插入到原调度方案的第4 块板坯后，依此类推。可以看出，虽然参与调度的板坯共计45 块，但染色体的基因位仅需设置5 个，且通过插入方式进行解码，在保证了解码效率的同时有效保障了约束（17）被满足。

3.2 概率模型的建立

相较于遗传算法的交叉变异操作，EDA 通过概率模型的建立和更新来描述种群进化趋势。概率模型是EDA 的核心，设计合适的概率模型和更新机制对EDA 的性能起着决定性的作用。本文设计了适用于热轧重调度问题特点的概率模型，以提高解决实际生产难题的合理性和有效性。

本文算法采用n2行n1列的概率模型Pt表示解空间的分布概率，其中t表示进化代数。根据个体编码策略，定义了第t代概率模型矩阵Pt，如式（24）所示：

其中：j表示新板坯序列的索引；i表示原板坯序列的索引表示第t代第j块新板坯插入到原调度方案中板坯i紧后位置的概率。

算法选取初始种群中适应度值最大的SPsize个个体构成优势种群。由于染色体采用基于订单插入位置的编码方式，即每个个体内部基因是离散的，概率模型Pt为优势种群中每块新板坯插入原调度的位置在染色体中每一基因的统计概率。为提高EDA 的全局搜索能力，应保证所选初始种群的随机性和均匀性。本文采用概率均匀分布的方法构建初始概率模型矩阵P1如下：

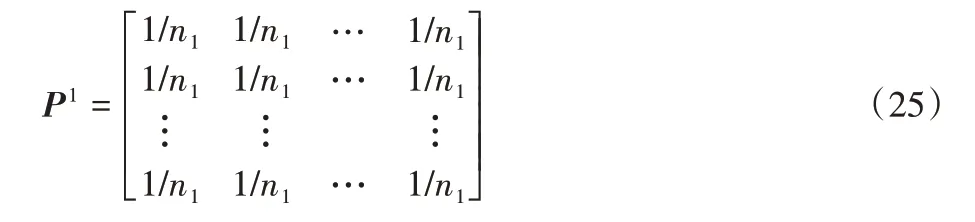
根据初始概率模型随机生成Psize规模的个体，计算目标函数值选取最优的SPsize个规模的个体，并基于优势群体采用如下更新机制更新概率Pt+1。

3.3 概率模型的更新机制

EDA 新种群的产生依靠概率模型的统计学习公式，使子代个体可以较大程度地保留父代个体的优良基因，因此一个合理概率模型的更新机制对EDA 性能至关重要。为了使概率模型更准确地表示群体的进化趋势，算法依据问题模型特征设计概率更新模型。更新概率模型Pt采用机器学习中Hebb 规则，选择SPsize个规模最优适应度函数个体构成优势种群，根据第t代优势群体在解空间中的统计结果，更新在下一代个体采样过程中所依赖的概率模型，即

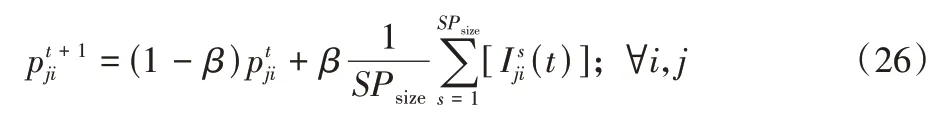
其中：β（0＜β＜1）表示学习因子表示第t+1 代第j块新板坯插入原调度方案板坯i后位置的概率；SPsize表示优势种群规模；s表示个体表示第t代个体s的解空间统计函数。的赋值方式如下：

通过不断地迭代，使概率矩阵趋于成熟。在每次迭代中，通过概率矩阵Pt对个体从第x1位至第位顺序采样，对待确定个体的位置xj通过轮盘赌的方法选择板坯i，板坯i被选择的概率为。采样生成新种群后，通过适应度函数选择优势群体，基于优势种群采用概率模型的更新机制更新概率矩阵Pt，如此反复。在每次计算适应度函数选择优势群体时采用精英保留策略以保证算法收敛，直到达到最大迭代次数，计算得出最优解。

3.4 适应度函数

取目标函数式（1）的倒数作为适应度函数。求解算法时可能出现同一轧制单元内约束（13）～（16）同宽板坯超过最大限制，板坯宽度、厚度和硬度变化不平滑等不满足模型约束条件的调度解。为满足约束条件，保证解的可行性，将目标函数式（1）调整为：

其中：F′为修正后的目标函数；F为原目标函数；M为足够大的正整数。违反任一约束条件，调度解经过计算得到的目标值均为极大值，那么适应度值则极小，通过轮盘赌方法选择到该个体的概率接近0，大幅降低了该个体进入到下一代的概率，进而达到识别并淘汰不可行解的目的。

3.5 算法步骤

在求解考虑订单扰动因素的热轧重调度问题时，基于EDA 的求解步骤如下：

步骤1 输入算法参数，包括种群规模Psize、优势群体规模SPsize和学习因子β等；

步骤2 初始化种群Psize及随机概率矩阵Pt，迭代次数t=0；

步骤3 计算种群个体的适应度函数；

步骤4 根据适应度值从Psize中选取优势种群SPsize；

步骤5 根据优势种群SPsize更新概率模型Pt；

步骤6 采用精英保留策略保存记录该优势种群的最优解best，并对概率模型随机采样生成新一代优势种群SPsize；

步骤7 计算新一代优势种群SPsize个体的适应度函数，更新迭代次数t=t+1；

步骤8 若t=Tmax，输出最优完整解和目标值，否则转至步骤5。

4 实验与结果分析

4.1 实验环境与数据

为验证本文模型和分布估计算法性能，设置对比算法进行实验。目前未发现有公开发行的将紧急订单插入热轧生产调度问题和分布估计算法结合的文献，没有类似标杆算法可以对比，因此本文与经典遗传算法进行比较。本文设计的两个对比算法如下：

1）传统遗传算法（Traditional Genetic Algorithm，TGA），在热轧调度中广泛应用，解决调度问题经典有效［1］。算法采用本文针对待插入工件位置的编码策略，传统遗传算法的进化策略参考文献［1］。

2）单亲遗传算法（Parent Genetic Algorithm，PGA），采用本文的编码策略，基于文献［5］的单点基因换位方式执行交叉操作。

本文选用某大型现代化钢铁联合企业炼钢厂的实际生产订单数据进行实验，采集了合理的初始调度方案及新订单数据样本。将初始调度方案板坯的数据按照板坯编号、板坯所属轧制单元、所属订单交货期、轧制宽度、轧制硬度、轧制厚度、轧制长度、轧制时长等属性整理；将新订单的数据按照板坯编号、所属订单交货期、轧制宽度、轧制硬度、轧制厚度、轧制长度、轧制时长等属性整理；将初始调度方案轧制单元的数据按照轧制单元编号、轧制数量、轧制单元时长、轧制长度等属性整理。由于新板坯到达时间的不确定性，采集了板坯的不同到达时间作为数据样本进行仿真实验。由于钢铁企业中板坯的轧制时长一般用分钟（min）计算，交货期用天（day）计算，因此为方便统计，统一单位为min。基于该炼钢厂的实际情况并借鉴已有文献确定轧制宽度、硬度、厚度的跳跃惩罚值如表1～3 所示，拖期惩罚系数可依照工厂实际对拖期和跳跃惩罚的权重确定，本文依据某大型现代化钢铁联合企业炼钢厂的设定数据，令α=0.5；根据某炼钢厂的实际生产情况，并根据参考文献［19］，确定每个轧制单元总长度限制为Qmax=40 km，同宽板坯轧制长度限制为Lmax=100 km，换辊时间为s=30 min。

表1 宽度跳跃惩罚值Tab.1 Width jump penalty value

表2 硬度跳跃惩罚值Tab.2 Hardness jump penalty value

表3 厚度跳跃惩罚值Tab.3 Thickness jump penalty value

由上述采集到的数据样本，将问题规模设置为新板坯到达数量n2=50，100，150，200。对于板坯到达时间的设置，考虑到实验数据设有5 个轧制单元，在初始调度方案中的开始轧制时间依次为0 min、1 020 min、1 370 min、1 830 min、2 130 min，因此依据前3 个轧制单元的开始轧制时间设置了板坯到达时间t=200，1 020，1 370。根据问题规模进行12 组仿真实验，每组随机生成20 个算例。经测试，运行设置参数如下：种群规模M=200，优势种群数量B=70，学习速率β=0.3，最大迭代次数T=500。由于每个重调度时刻参与重调度的板坯数量不同，为方便比较分析，运行参数与上述设置相同。

实验分为两部分：第一部分为算法性能分析，对相同的问题采用不同的算法评估比较；第二部分针对本文算法，设计了新板坯数量和板坯到达时间对重调度性能的影响实验。本文算法使用Matlab R2020a 编写，运行在Intel i7-1065G7 CPU@1.30 GHz 1.50 GHz/8.00 GB 的硬件环境下。

4.2 算法性能分析

算法的性能从有效性和运行时间两方面对比分析。在有效性方面，以目标值为评价指标。针对12 组问题规模分别用上述算法求解，分别计算每种算法的均值avg和标准差Std，并采用方差分析（ANalysis Of VAriance，ANOVA）对每组实验进行显著性检验（γ=0.05）。实验结果见表4，最后两列为每组实验方差分析的F和P-value值。在运行时间方面，上述算法求解不同问题规模的处理时间（CPU 时间）如表5所示。

表4 不同算法的均值、标准差和方差分析的对比分析结果Tab.4 Comparative analysis results of different algorithms of mean，standard deviation and variance analysis

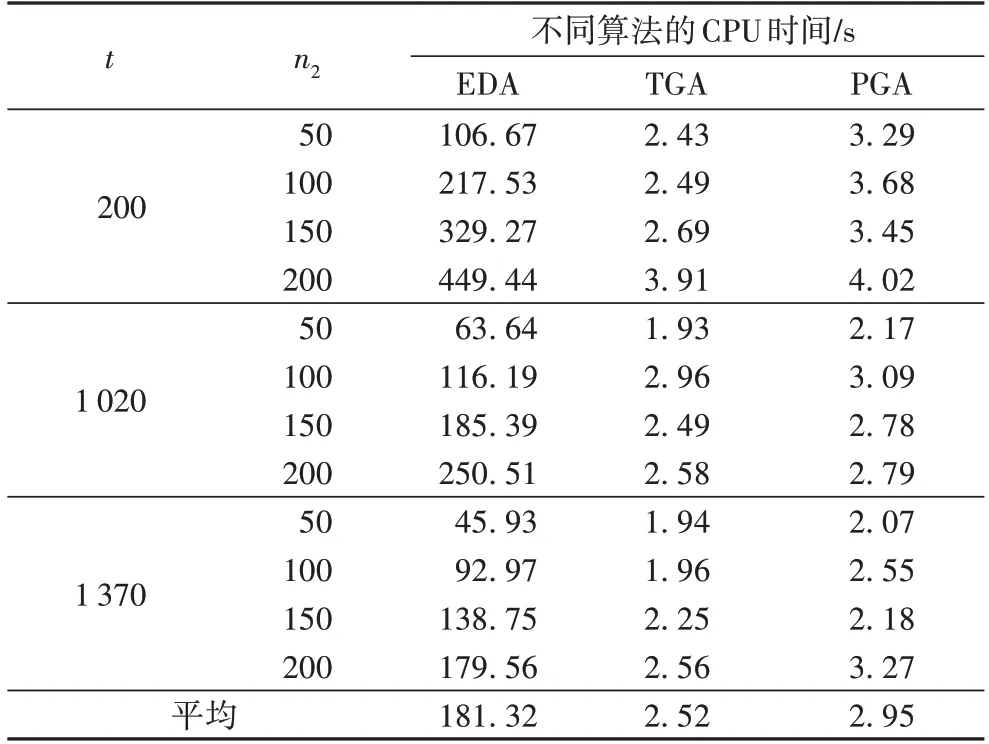
表5 不同算法的CPU时间对比Tab.5 CPU time comparison of different algorithms

从表4 的avg指标和std指标来看，除了1 020×50 的规模问题外，EDA 在其他规模问题上均取得了最小平均值。说明在EDA 迭代过程中通过概率模型的更新学习保留了优势个体基因，使优良基因概率不断增大，从而引领新一代优势个体的产生。EDA 的avg和Std的平均值均为最低值，说明EDA 的寻优能力强，求解稳定性好。每组实验进行ANOVA分析得到的P-value均小于0.05，且随着n2或者t的增加，P-value呈显著下降趋势，说明三种算法对于调度目标值存在显著影响，而且随着板坯数量增加或到达时间增加，差异愈加明显，从而验证了本文所提EDA 的优越性。

从表5 的CPU 指标角度来看，针对不同的问题规模，TGA 和PGA 的求解效率均高于EDA，这是由于选择优势群体以更新概率模型导致的。相较于TGA 和PGA 在初始种群上进行的交叉变异操作，EDA 基于采样生成了新优势群体从而进行概率模型的学习与更新，导致求解时间较长，但是EDA 在寻优能力和求解稳定性上均优于其他算法。而且目前多数钢铁企业对热轧批量计划采用人工编排的方式，对考虑订单扰动的热轧重调度问题，人工编排的效率低、耗时长，EDA 的计算时间显然小于人工编排的时间。即使对板坯到达时间较早（t=200 min）和大规模新板坯到达（n2=200）的情况下，EDA 也能在450 s 内给出调度方案，因此该算法解决了钢厂实际存在的问题，完全满足生产需要。

为更直观反映本文设计算法的收敛效率和寻优能力，随机挑选一个规模为100×200 的算例，图4 给出了三种算法在迭代500 代时的收敛曲线对比。

图4 不同算法的收敛曲线对比Fig.4 Comparison of convergence curves of different algorithms

从图4 可以看出，在收敛效率上，EDA 在132 代取得了稳定值，而TGA 在301 代取得了稳定值，收敛速率不及EDA；在寻优能力上，EDA 的目标值为75 均低于TGA 和PGA 的目标值152 和135。虽然PGA 和EDA 的收敛效率相差不大，但EDA 得到的解明显优于PGA。以上结果表明，EDA 具有良好的收敛效率和求解质量。

三种算法的目标值均低于目标函数设置的惩罚值M，说明了结果的有效性，从而验证本文的模型和算法能够解决热轧重调度问题。

4.3 新板坯数量和到达时间对重调度性能的影响

新板坯数量n2和板坯到达时间t是影响重调度性能的关键参数，本节分别探讨两种因素对重调度性能指标的影响。对于新板坯数量的影响，本节对4 个实验组n2=50，100，150，200 的目标值进行均值及95%置信区间的分析，如图5 所示。对于板坯达到时间的影响，对3 个实验组t=200，1 020，1 370的目标值进行均值及其95%置信区间的分析，如图6 所示。

1）新板坯数量对重调度目标值的影响。

图5 中的每条曲线表示了相同到达时间下，重调度目标值随新板坯数量增多所呈现出的变化趋势。当板坯到达时间t一定时，调度目标值随新板坯数量n2的增加呈逐渐增长的趋势。随着新板坯数量的增加板坯间的总跳跃惩罚和订单拖期惩罚的总和增大。当新板坯数量从50 增加到100 时，增长较为缓慢；当新板坯数量从100 增加到150 时，曲线斜率变化较为明显；当新板坯数量从150 增加到200 时，由于板坯密集到达，跳跃惩罚增加且参与重调度的原板坯延后时间较长导致拖期惩罚增加，因此曲线斜率显著增大。以上分析说明新板坯数量的增加对调度目标值的增长幅度影响较为显著；并且置信区间没有重叠，表明针对板坯的不同到达时间对重调度目标值有较为显著的差异。

图5 板坯的到达数量对目标值的影响及其95%置信区间Fig.5 Influence of arrival quantity of slab on target value and its 95%confidence interval

2）板坯到达时间对重调度目标值的影响。

图6 中的每条曲线表示了相同新板坯数量下，重调度目标值随板坯到达时间增大所呈现出的变化趋势。随着板坯到达时间t的增大，尚未轧制的原板坯数量减少，新板坯可选择的位置减少，导致跳跃惩罚增大，且生产调度临近交货期导致订单拖期惩罚增大。

图6 板坯的到达时间对目标值的影响及其95%置信区间Fig.6 Influence of arrival time of slab on target value and its 95%confidence interval

由图6 可以看出，曲线在整体上呈现增长的趋势。这是由于随着时间的推进，新板坯到达数量在板坯总量中的占比增加，对目标值有一定影响。200 ＜t≤1 020 时，新板坯相较于原板坯数量占比不大，因此板坯到达时间对重调度目标值影响较小，曲线增长相对缓慢；1 020 ＜t≤1 370 时，新板坯占比变大，对目标值的影响逐渐增强，曲线斜率呈现增大趋势，因此曲线的增长幅度会逐渐加大；随着板坯到达数量的逐渐增多，在板坯总量中的占比增加，因此数量较大时曲线的增长幅度要大于数量较少时的增长幅度。以上分析说明：板坯到达时间的增加对调度目标值的增长幅度影响呈现逐渐增强的趋势，且随着新到达板坯数量的增加，该趋势表现得更为明显。图中置信区间没有重叠，表明针对板坯的不同到达数量对重调度目标值有较为显著的差异。

5 结语

本文针对订单到达的情况导致热轧生产过程中出现扰动的问题，以最小化订单拖期惩罚和板坯间总跳跃惩罚加权和为优化目标展开研究。首先，根据紧急订单到达这类动态事件在热轧生产中的特点，以新到达的板坯和发生扰动时尚未轧制的板坯作为重调度对象，设计了基于事件驱动策略的重调度方法和流程，提出了考虑订单扰动的热轧重调度优化模型。进而，针对基于订单扰动的热轧重调度的问题特点，设计了一种分布估计算法。该算法具有以下特点：1）采用基于插入位置的方式进行编码，以缩短编码长度并减少解码步骤，进而提高求解效率；2）定义了基于惩罚值的适应度函数，通过惩罚机制实现对不可行解的识别与淘汰；3）根据问题特征设计了概率公式并更新了概率模型，根据进化趋势动态指导种群的进化方向；4）引入精英保留策略保存每一代的最优解，以保证算法的收敛性。最后，基于国内某大型现代化钢铁联合企业的实际生产数据，设计了仿真对比实验，验证了该模型和算法的有效性，并检验了动态到达的订单数量和到达时间对热轧生产调度的影响。实验结果表明，板坯到达时间的增加导致调度目标值的明显增长，且随着新到达板坯数量的增加，调度目标值的增长幅度明显加大，这两种因素对于调度目标均有显著影响。因此，如何考虑设置合理的订单数量阈值作为重调度的触发机制将是我们下一步的研究方向。