面向智能工厂原料供应环节的多机器人任务分配方法
熊乾程,董 晨,洪祺瑜
1(福州大学 数学与计算机科学学院,福州 350116)
2(福建省网络计算与智能信息处理重点实验室,福州 350116)
3(网络系统信息安全福建省高校重点实验室,福州 350116)
E-mail:dongchen@fzu.edu.cn
1 引 言
如今,全球性的产能过剩导致了企业间越发激烈的竞争,而互联网的飞速发展大幅降低了人与人之间交流成本,进一步放大了客户个性化的需求,在这样一个技术、经济快速增长的环境下,越来越多的企业从传统的大规模生产向着能够实时收集生产信息,调整产品类型与生产能力的多品种、多批次智能化生产转变[1].客户的定制生产需求带来了产品生命周期的多变性,工厂需要更加灵活的制造自动化以适应动态的制造与供应过程.然而,传统的制造应用中各生产环节大多是单独且分离的,生产实体与虚拟系统的集成度较低,存在生产环节难以及时调整、供应效率低下等问题[2],难以满足如今技术发展与客户需求的快速变化,急需制造商重新配置生产路径与流程,重组制造单位.
面对生产制造需求快速变化带来的挑战,德国政府于2010年提出了智能工厂这一概念,作为工业4.0的核心,智能工厂旨在构建面向制造业的信息物理系统,由物理实体负责生产中的智能协商,信息系统负责任务收发、数据采集以及实体生产过程的监督,通过集成信息系统与物理实体,最终实现工厂中机器、原料、产品极其的自组织生产[3].
作为生产环节中的重要一环,灵活的原料供应是多类型、多批次产品生产的基础,自动引导车(AGV)、自主移动机器人(AMR)等技术的进步给传统的物料搬运市场带来了新的解决方案,仓储和制造设施内的自动负载运输被认为是提高生产效率、降低运营成本的实用手段并广泛运用在自动化生产制造环节[4],尽管具备许多优势,在面对定制生产带来动态原料供应需求变化时,多机器人系统需要更加高效且具备伸缩性,如何在供应环节为自动负载运输机器人系统的分配任务仍旧是个亟待处理的问题[5].为了满足动态供应需求、解决供应问题,我们提出一种运用运筹学理论的启发式智能工厂多机器人供应分配方法,能够在面对不同的任务规模与机器人的数量时,在保证任务完成质量的情况下,进一步优化分配结果.本文的主要贡献如下:
1)考虑原料供应需求与运行距离等因素,设计了用于反应供应任务的执行效果以及机器人消耗的效用与成本函数,根据设计的效用与成本函数,建立了一个最大化供应任务收益的智能工厂原料供应优化模型.
2)将基于多机器人系统的任务协作应用在原料供应环节,将原料供应转化为多机器人任务分配问题的变体,提出一种基于博弈论的多机器人协作的供应任务分配方案.
2 相关工作
由于在重复工作中的高速度、精度,以及解放人工成本带来的生产效益,在过去的几年里,多机器人系统在开始广泛集成在运输、仓储、工业制造等领域[6-8],如何平衡效率、资源、成本等因素为多机器人系统合理的分配任务,已经成为当前研究的热点[9],很自然地让人考虑如何将多机器人系统应用于智能生产环节.
Huang等人[10]提出了一种基于拍卖算法的智能工厂中的分布式机器人协作任务分配机制,考虑了异构机器人与任务距离以及机器人能力与任务之间的匹配程度进行任务划分;Baroudi等人[11]提出了一种基于动态多目标拍卖的任务分配算法,综合机器人的任务完成质量、负载平衡以及运行距离三个指标设计了新的效用函数,并在现实场景中模拟了算法的有效性.基于市场机制的任务分配方法能够考虑各机器人的结构特性,并结合不同指标快速产生机器人的任务分配,但是在工作时各系统独立运行,面对突发任务状况无法及时响应,且任务大多仅由单个机器人负责执行,机器人资源无法得充分利用.
Afrin等考虑了工厂中的应急管理问题[12],使用改进多目标遗传算法NSGA-II对时间、能源和成本属性进行优化,为应急管理服务多机器人系统分配资源,比原始遗传算法具有更强的寻优能力,改进可运用于现有的多个多目标优化算法,取得了至少提升18%性能的表现,但在收敛速度上显得比较缓慢.
Lee等人[13]提出一种智能工厂中无人机在线雾计算任务分配框架,考虑通信与计算等待时间设计了一种在线贪心算法,能够在线优化无人机任务分配,决定使用哪台无机人进行雾计算,所提出的在线算法能够以不超过7.5%的差距实现接近最优的任务分配.
近年来,一些学者借鉴经济学中的博弈理论,通过启发式改进应用于任务分配中,综合速度与分配质量取得了不错的成果[14-15],针对上述智能工厂种任务资源分配存在的问题,提出一种能够适应智能工厂中不同规模任务要求,保证分配质量同时实现快速分配响应的多机器人任务分配方法是十分必要的.
3 智能工厂中的供应问题
3.1 场景描述
如图1所示,在智能工厂的供应问题场景中,工厂中存在多条生产线以应对不同需求的生产任务,工厂从客户处接受需求订单,原料供应由供应机器人承担,任务经过云计算分解得到数字化供应需求,由工厂内生产设施对空闲的供应机器人进行广播后得到供应任务初步分配,供应机器人之间通过通信后进一步调整确定最终的资源运送方案,执行对应订单任务的机器人从仓库中将材料取出并补充至对应生产线,供应机器人同一时间只能执行一项供应任务,每个供应任务需要一个或多个供应机器人完成.
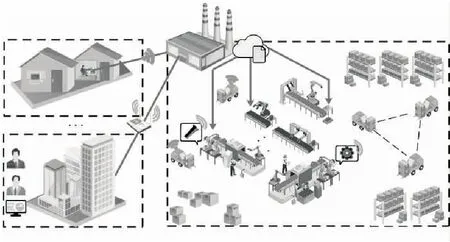
图1 智能工厂动态生产示意图Fig.1 Illustration of a dynamic production in smart factory
3.2 表示与前提
使用T(t1,…,tn)代表一系列材料供应任务,每个任务需要机器人将要求的生产材料补充至对应的生产线,其中,运送任务由移动供应机器人R(r1,…,rm)承担,供应机器人之间都是同质的,对于每个可执行任务,机器人之间都可以相互交换;生产由位置固定的制造生产线MR(mr1,…,mrl)执行,供应材料M(m1,…,mk)贮存在仓库W(s1,…,sk)中.
下标m,n分别代表定制化生产任务与供应机器人的数量,其中m满足m≫n,机器人的rm的位置由Prm表示,制造生产线mrl的位置由Pmrl表示,供应材料次序与仓库一一对应,mk的位置由Pmk表示.在确定将供应机器人ri分配给对应任务tj后,将获得一个效用U(ri,tj)用于表示机器人ri对与任务tj的执行效果,供应任务T的整体执行效用U(如式(1)所示)通过各任务的效用加和表示:
U=∑mi=1∑nj=1xijU(ri,tj)
(1)
其中xij∈{0,1}表示供应机器人ri对于订单任务tj的执行状态;同时,存在一个成本函数cost(ri,tj)用于反应供应机器人输运的消耗,这个成本函数与运行距离成正比,用Cost反应执行对应任务的机器人的消耗总和,如式(2)所示:
Cost=∑mi=1∑nj=1xijcost(ri,tj)
(2)
为完备供应机器人工作环境,本文在此对供应任务与执行场景做出以下假设:
1)供应场景在一个大小为length×width的矩形工厂进行.
2)当前工作场景环境已知,执行供应任务时机器人无须考虑创建环境地图.
3)供应机器人初始位于工厂内随机位置,能够实时获取当前任务与自身位置信息.
4)订单任务之间不存在顺序依存关系,供应机器人可按各自偏好自由执行任务.
3.3 供应问题模型
由于供应机器人的同质性,对于相同材料的机器人具有相同的运送能力,通过云端的计算分解可以得到当前各供应任务所需的机器人数,结合各任务所需的机器人数设计得到任务tj的效用表示如式(3):
U(tj)=Cj-Cj-∑mi=1xij
(3)
其中Cj代表任务tj需要的供应机器人数量,xij∈{0,1}表示机器人ri对于任务tj的执行状态.对于供应任务t,过多的机器人分配会导致资源的浪费,过少的机器人数量则会影响任务的完成,最大效用加和MAX_UTILITY在满足每个任务t的分配数量要求后达到[16]:
MAX_UTILTY=∑nj=1Cj
(4)
供应机器人ri为完成供应任务tj,将生产材料mk运输至生产线mrl处的消耗表示如式(5)所示:
cost(ri,tj)=ωd(Pri,Pmk)+d(Pmk,Pmrl)2(length+width)2+ε
(5)
其中d表示两个位置的距离函数,ε是一个大于零的常数,ω代表权重系数,供应问题的总收益是供应任务整体执行效用与执行对应任务的机器人消耗总和的差值,结合效用与成本比函数建立供应问题优化模型如式(6)-式(9)所示,以期在最大化效用加和的同时最小化执行对应任务的机器人成本:
max∑nj=1U(tj)-∑mi=1∑nj=1xijcost(ri,tj)
(6)
s.t.Cj-∑mi=1xij=0 ∀tj∈T
(7)
∑nj=1xij≤1i=1,…,m
(8)
xij∈{0,1}i=1,…,mj=1,…,n
(9)
式(7)要求每个任务分配得到其需求的供应机器人数量,式(8)限定了供应机器人在同一时间只能执行一项任务.在此,定义解决方案π,对于给定的m个供应机器人与n个供应任务,每个任务tj需要Cj个供应机器人完成,方案π代表全体满足供应任务要求的可能任务分配解决方案,目的是找到最大化供应总收益的方案π*如公式(10-14)所示:
π*=argmaxprofit(π)
(10)
其中:
profit(π)=U(π)-Cost(π)
(11)
U(π)=∑nj=1U(tj)
(12)
Cost(π)=∑mi=1∑nj=1xijcost(ri,tj)
(13)
且满足:
U(π*)=MAX_UTILITY
(14)
4 基于博弈论的供应任务分配算法
在博弈论中使用的最广的解是John F. Nash提出的均衡概念[17],对于一组行动剖面a,每个参与者i采取行动记为ai,存在行动剖面a*,对于每个参与者i,有:
(a*-i,a*i)i(a*-i,ai),∀ai∈a
(15)
其中a*-i表示除了参与者i外其他所有参与者采取的最优行动序列,对于参与者i,当没有其他行动产生优于选择a*i的结果时,称这个行动剖面为满足纳什平衡[18].纳什平衡体现了当前行动组合的稳定状态,对于该状态每个参与者拥有对于对其他参与者行动的正确预期,并坚持自己的行动不产生偏移.
基于博弈论的任务分配算法主要可分为两步骤,首先根据机器人对可执行任务的偏好,通过贪婪选择快速分配满足任务需求数量的机器人划分;各机器人再通过与工厂内其他机器人交换当前执行的任务信息,进一步优化划分的结果,寻找任务的稳定分配,算法整体流程如图2所示.

图2 分配算法整体流程Fig.2 Overall flow chart of allocation algorithm
4.1 基于贪心的任务初始划分
由上述模型可知,所提出的智能工厂内供应任务方案要求在给出满足任务需求的机器人数量分配同时,最小化供应机器人的总体损失.在此首先定义执行任务T的供应机器人偏好矩阵Bm×n=(bij),bij计算如式(16)所示:
bij=ln(1-cost(ri,tj)cost(ri,tj))
(16)
bij反应了供应机器人ri与任务tj间联系的紧密程度[19],bij越高代表供应机器人ri越倾向于执行任务tj.供应机器人对当前所有可执行任务计算各自偏好,作为报价向任务点发送讯息,工作台根据任务要求的机器人数按报价从高到低选取执行任务的机器人,算法伪代码如下所示:
算法1.基于贪婪策略选择的任务划分
输入:机器人R、任务T坐标
输出:任务分配集合S
Foreachri∈R、tj∈Tdo
Calculatebij
Endfor
ForeachSj∈Sdo
Sort thebijreceived from each supply robot in descending order for each task
Select the robots in order until |Sj|=Cj
record the highest bias of each robot for executable tasks asmax(bi)
Endfor
IfS1∩S2…∩Sn+1=∅
Go to the next stage to find the equilibrium solution
Else
Foreachri∈R、Sj∈Sdo
ifri∈Sjandbij≠max(bi)
removerifromSj
Endfor
Foreachri∈Sn+1、Sj∈Sdo
Selectriwith the highestbijuntil |Sj|=Cj
Endfor
Go to the next stage to find the equilibrium solution
用S={S1,…,Sn+1}表示当前任务分配集合,其中Sj代表任务tj的供应机器人分配集合,j∈[1,n];Sn+1代表当前为未被分配的机器人的集合.由于初始划分没有考虑到供应机器人的限制条件,可能会出现单个供应机器人被分配到多个任务的情况,供应机器人对此选择自己偏好最高的任务执行,造成的其他任务的机器人缺省通过贪心算法选择当前未分配任务的供应机器人的最高报价,在满足所有供应任务机器人数量要求后,进入下一阶段求取任务划分的平衡解.
4.2 求取区域平衡解
经过节4.1的任务初步分配后,我们得到一个不相交的供应任务机器人划分集合S={S1,…,Sk+1},对于每个集合Sj,满足:|Sj|=Cj,j∈[1,n].用集合P={Ps1,…Psk+1}表示供应机器人任务分配集合的执行效用,其中PSj表示集合Sj对于任务tj的执行的效果,PSUM表示当前任务划分的总体效果:
Psj=∑ri∈Sjbij
(17)
PSUM=∑nj=1Psj
(18)
求取供应任务分配的平衡解就是一个寻求稳定的任务划分区域的过程,在该稳定状态下,没有任何一对完成通信的供应机器人能在其它机器人保持原有动作的状态下通过交换自己的行动使得当前任务划分的总体效果更优.供应机器人通过自身广播与工厂内其他机器人交换执行任务的讯息以及对于当前分配任务的偏好.在通信过程中,对于执行供应任务ti的机器人rp与执行供应任务tj的机器人rq,若存在bpi+bqj 在基于贪心的初始任务划分部分,工作台按照机器人对各任务的偏好大小对收到的报价进行降序排列,最坏的时间复杂度为O(n*mlogm);在寻求区域平衡解时,供应机器人群体两两完成通信最多需要m(m-1)/2次交换,因此算法的整体时间复杂度为O(max{n*mlogm,m2}),能在多项式时间内得到一个满足任务要求的原料供应分配解决方案. 在实验环境方面,实验使用python3.6在win10操作系统上对所提出算法进行编程,处理器使用i5-4210H 2.90Hz,内存16GB;在实验参数设置上将模拟实验的矩形工厂大小设置为600X400,机器人与任务初始位置在工厂范围内随机生成,设置消耗权重系数ω为1,供应机器人数量从集合从区间[4,100]之间选取,任务数量从区间[2,30]之间选取,并保证任务数量小于供应机器人数1/2且任务要求的机器人数量加和不超过当前可用的供应机器人总数. 我们采用一个实验实例来展示供应任务的分配过程,选取机器人数m=15,供应任务数n=5,各任务所需供应机器人数用元组O1-5=(O1,O2,O3,O4,O5)表示且满足节5.1中的实验设置,任务分配总收益由全体执行供应任务的机器人效用之和与机器人执行任务所产生的消耗的差值得到,计算如式(3)-式(6),反映了任务分配的总体质量,作为实验的评判标准之一,表1展示了当前各可用供应机器人对任务的执行偏好,与计算如式(16).机器人根据自己的偏好对项任务发布点发送讯息,并按节4.1所示算法流程进行任务的初步分配,得到一个不相交的供应任务机器人划分集合;在求取区域平衡解阶段,供应机器人通过个体间的通信,寻找能够提升供应任务总收益的机器人任务分配新方案并调整当前分配,如图3所示,实验实例在经过9次迭代后收益达到最大并得到一个稳定的供应机器人-任务对分配. 表1 供应机器人-任务执行偏好Table 1 Task execution preference of supply robot 在这一部分,实验探索了供应任务分配面对新任务出现时收益的变化,固定供应机器人数从10至100,供应任务数量从5开始逐步上升,并在任务数量达到30时所需机器人达到当前机器人总数,取20次测试任务分配收益的平均值,结果如表2所示,定义的效用函数与完成参与完成任务的机器人数量挂钩,收益伴随任务的增加而增加;同时,由于在同一时间机器人只能执行一个分配任务的限制,参与到分配的机器人因为任务的增加而趋近最大值,会出现能够最大化某一任务的机器人已经被占用这一情况,因此效用的增长趋势会随着任务的增加而减缓. 图3 任务迭代与最终分配结果Fig.3 Iteration and final assignment of tasks 表2 不同机器人数量下任务数与收益Table 2 Number of tasks and profit under different number of robots 由于所提出的智能工厂内供应任务分配方案是在满足各任务需求的机器人数量前提下执行,根据效用计算式(3)、式(4)以及所建立的供应优化模型目标(6)-式(9),我们可以将算法性能比较转化为任务分配方案所产生成本消耗的比较,固定供应机器人数100,随着参与到供应任务的机器人数量增加,供应机器人个体间通信得到更优解的可能相应增长,如图4所示,在对比最小化成本的贪心算法时,我们提出的算法在任务数的增加时性能上进一步占优,并在任务数等于30时达到最高的19.5%. 图4 算法性能比较Fig.4 Algorithm performance comparison 在本节,实验固定任务数,保持供应机器人数增长,从成本角度与能得到最优结果的暴力匹配算法进行比较,取20次实验平均值,由于机器的限制,实验最多只能得到15个供应机器人与4个分配任务的最优结果.图5(a)展示了最小化成本算法与最优结果的成本比值,在任务数等于2时最优成本比值,从参与任务的机器人数量4时的82.2%开始随着机器人数量的增加逐渐提升,在机器人数量达到15时取得最高比值94.5%;在任务数等于4时性能下降到85%上下.在图5(b)中,任务数等于2时,所提出的算法面对不同机器人数量,与最优结果的比值均能够超过96%,最高达到99.3%;在任务数4时也能够至少达到最优成本结果的93%.从与最优结果的比值中可以看出,在损耗上所提出的算法能够找到非常接近最优结果任务分配解决方案. 图5 与最优算法的成本比较Fig.5 Cost comparison with optimal algorithm 算法面对不同任务与供应机器人数量时执行任务分配100次的平均时间如图6所示,在固定任务数时,任务分配时间随着供应机器人数量的增加呈现上升趋势;固定机器人数时,任务分配的时间也会随着任务数的增加而增加,总体而言,机器人与任务数量的增长对分配时间的影响并不显著,在面对给定100个机器人与30个分配任务时算法也能在很短的时间内(0.645秒)内给出分配结果. 图6 不同任务数量下算法执行时间Fig.6 Algorithm execution time under different number of tasks 在本文中,针对智能工厂下的原料供应问题,我们考虑任务需求与运行距离等因素,设计了效用函数U与成本函数cost用于反应供应任务的执行效果与产生的消耗,根据设计的效用与成本函数,构建了一个最大化任务收益的供应优化模型,提出一种基于多机器人协作的供应任务解决方案,通过算法分析与实验结果表明,所提出算法能够处理不同供应任务机器人规模,并在保证任务完成质量的同时在短时间内迅速实现任务分配,对比最小化成本的贪心算法具有较大优势.今后我们将考虑异构供应机器人的任务分配用以处理更加复杂的供应分配问题;未来还将考虑故障恢复进一步增强分配的鲁棒性.4.3 算法分析
5 实验分析
5.1 实验设置
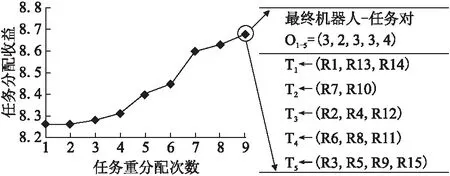
5.2 实验实例

5.3 收益与任务数

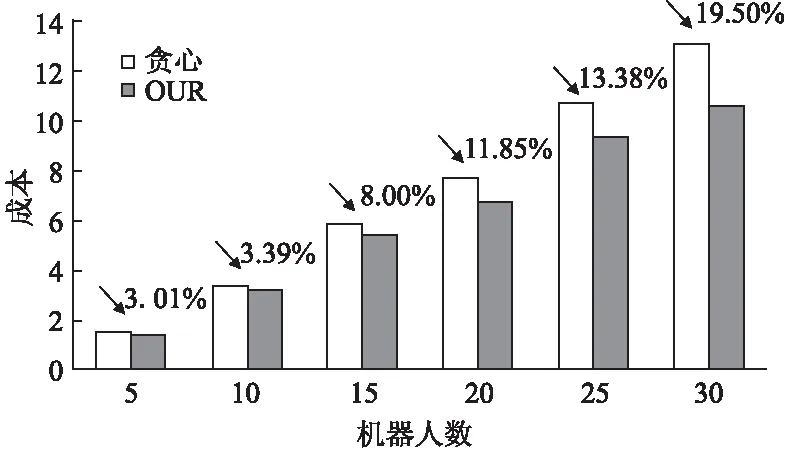
5.4 与最优结果对比

5.5 执行时间

6 结 论

