有限温度张量重正化群方法及其在阻挫量子磁性研究中的应用

李 涵 ，李 伟

1.北京航空航天大学物理学院，北京100191

2.中国科学院大学卡弗里理论科学研究所，北京100190

3.中国科学院理论物理研究所，北京100190

目 录

I.引言 121

II.有限温度张量重正化群方法与量子自旋模型计算 122

A.有限温度张量网络 123

B.指数张量重正化群 123

C.正方晶格海森堡模型的有限温度张量重正化群计算 124

D.阻挫三角格子海森堡模型的有限温度张量重正化群计算125

III.三角晶格阻挫磁体及Berezinskii - Kosterlitz - Thouless

相变 126

A.阻挫伊辛磁体TmMgGaO4的微观自旋模型 126

B.赝自旋映射与演生U(1) 对称性 127

C.低温热力学及谱学实验证实 128

IV.六角晶格Kitaev 阻挫磁体及高场自旋液体相 129

A.六角晶格Kitaev 模型 130

B.有限磁场下的Kitaev 模型与分数液体 131

C.Kitaev 候选材料α-RuCl3133

D.α-RuCl3微观自旋模型 133

E.场致量子相变与有限温度–磁场相图 134

F.强磁场自旋液体态 136

V.总结与展望 137

致 谢 139

参考文献 139

I.引言

在传统的凝聚态物理范式下，自然界中形形色色的物质形态多是由对称性及其自发破缺所支配的。具体到磁性系统，在温度相对较高时，由于系统具有很强的热涨落，自旋的指向是随机且无序的，此时系统保持在高对称性的顺磁相。而当温度降低时，系统通常会破缺一定的自旋相关对称性，进入到如铁磁、反铁磁、亚铁磁等长程磁有序相，或共价键固体态等破缺晶格平移对称的磁无序相。在这样的对称破缺图景之下，朗道–金兹堡–威尔逊(Landau-Ginzburg-Wilson，LGW) 理论构成了人们对磁性物质态理解的标准范式。

然而，凝聚态物理工作者也在不断追求突破LGW范式的新奇物态与相变，并将注意力集中在自旋相互关联和纠缠的低维磁性体系中。早在上世纪70 年代Berezinskii[1]以及Kosterlitz 和Thouless[2,3]在二维XY 磁性体系中各自独立地发现了一种新奇的拓扑相变：系统在低温下并不破缺对称性，因此没有形成严格意义上的长程序，此时自旋关联函数随距离代数衰减；但是随着温度升高系统会历经非解析的奇异性，发生Berezinskii-Kosterlitz-Thouless(BKT)拓扑相变，这对应于拓扑型激发—— 涡旋对的耦合与解耦。实验研究者们曾经在液氦薄膜[4]和魔转角石墨烯超导[5]等体系中探测到过BKT 相变，然而在最早被提出存在BKT 相变的二维磁性系统中却鲜有报道。更为有趣的是，在阻挫磁体中，U(1) 对称可以自发地涌现出来并对应发生BKT 拓扑相变[6]，这一新颖的演生物理是否能在实际低维磁体中被实现，是量子磁性研究中待探索的有趣问题。

阻挫磁体展现出的另一类重要新奇物态是量子自旋液体[7–10]。在量子涨落影响下，这类系统降至极低温也无法形成常规的对称破缺自旋“固态”序，但是可以形成长程纠缠(拓扑序)，并伴随有自旋分数激发等新颖的量子性质。近年来，在模型中寻找自旋液体的理论研究取得了系列进展，人们在Kitaev 蜂巢模型(严格可解)[11]、笼目晶格海森堡模型(数值计算)[12,13]、三角晶格阻挫系统(数值计算)[14–16]等理论模型中发现了自旋液体态存在的证据；然而，人们是否能够在真实材料系统中观察到这样新奇的磁性物态，是备受关注的前沿问题。

另一方面，低维量子磁性材料体系作为典型的关联系统，对其进行深入研究需要借助高精度的多体计算方法，特别是有限温度和动力学计算等方法。近年来，有限温度张量重正化群方法，包括转移矩阵重正化群[17–19]，有限温度张量网络态方法等[20–31]在精确计算一维和二维量子格点系统的热力学性质上取得长足进展。这些方法可以用于定量分析实验热力学测量数据、确定微观自旋模型，进而深入探讨低维磁性体系中的新奇量子物态和相变。沿此量子磁性系统的多体计算研究路线，作者与合作者最近在若干三角和Kitaev 六角晶格自旋液体候选材料的研究中取得系列进展。

在下文第 II 节中，作者首先介绍近年来发展的有限温度张量重正化群方法及其在量子自旋模型有限温度计算方面的应用。在第 III 节中，介绍稀土磁体TmMgGaO4的微观模型与拓扑相变方面的进展，在第IV 节中介绍六角晶格Kitaev 磁体α-RuCl3的微观模型与高场自旋液体态。最后，在第V 节中对张量重正化群方法及其在若干重要阻挫磁性材料体系研究中的应用作一总结与展望。

II.有限温度张量重正化群方法与量子自旋模型计算

对实际磁性材料准确建立微观自旋模型并对多体性质开展精确分析，是人们研究低维量子磁性的可靠途径。精确的微观模型分析集中反映了人们对相关阻挫磁性材料系统的研究和理解程度。然而，建立量子磁体的模型并确定其参数具有很大的挑战性。而这一困难又主要来源于量子多体问题精确计算的复杂性：希尔伯特空间维度会随着系统格点数N的增加而呈指数级增大，即对于局域希尔伯特空间维度为d，系统尺寸为N的量子多体模型，其总空间维度为dN(如图1(a)所示)，计算代价指数增加而面临“指数墙”问题。因此，除了极少数可以严格解析的模型和问题，对自旋模型特别是阻挫自旋模型开展精确计算得到实验可观测物理性质是十分困难的多体问题。另外，由于实验测量的磁矩、磁化率、比热容等可观测量是在有限温度下进行的，所以人们在计算时还需引入温度变量，进一步增加了计算难度。

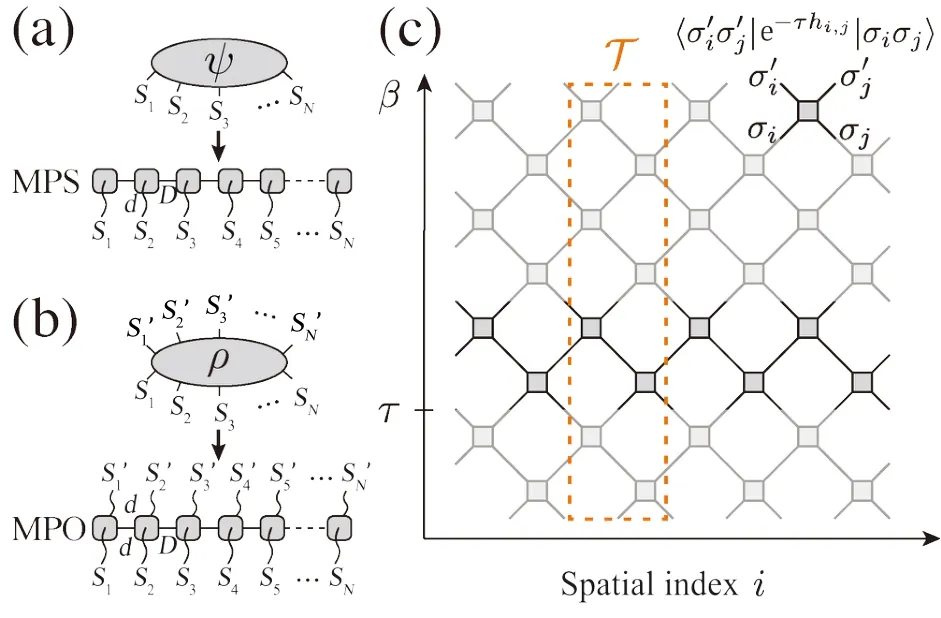
图1.(a) 希尔伯特空间维度为dN 的多体波函数ψ 写作维度为N ×(dD2) 的矩阵乘积态(Matrix Product States,MPS) 形式。(b) 维度为d2N 的多体密度矩阵ρ 写作维度为N ×(d2D2) 的矩阵乘积算符(Matrix Product Operator,MPO) 形式。(c) 利用Trotter-Suzuki 分解将密度矩阵ρ ≡e-βH 拆分成“棋盘格”有限温度张量网络，其中橙色框内表示转移矩阵T。

在过去二三十年的研究中，人们发展了一系列精确高效的有限温度多体计算方法，包括有限温度精确对角化(Finite-temperature Lanczos,FTL)[32,33]、量子蒙特卡洛(Quantum Monte Carlo, QMC)[34,35]及本文中主要介绍的有限温度张量网络态及其张量重正化群(Tensor Renormalization Group,TRG)[17–31]方法等。其中，FTL 方法是数值严格的方法，但处理的格点尺寸有很强的局限性；QMC 方法在模拟阻挫系统时通常会遇到符号问题；而基于有限温度张量网络态的重正化群数值方法则不存在这些限制，可以计算大尺寸二维系统的低温性质，为研究阻挫量子磁性系统提供了有力的工具。下面对张量重正化群方法做简要介绍。

张量网络态是量子多体系统的基态波函数和有限温度密度矩阵等的精确高效参数化方式，其图像表示如图1(a)-(b) 所示。在凝聚态物理领域中，人们关心的纯态或者有限温度混合态往往满足纠缠面积律并可以被张量网络精确地描述[36]。具体地说，在有限温度多体系统中，人们的研究对象是密度矩阵ρ ≡e-βH，其中β ≡1/T为多体系统的倒温度，而H为多体系统的哈密顿量。尽管H中存在大量的本征态超越纠缠面积律而难以通过张量网络态来有效表达，但是有限温度密度算符ρ(β) 仍满足互信息的面积律，可以有高效和精确的有限温度张量网络态表达。关于有限温度张量网络态及其重正化群方法的基础介绍可以参考中文综述文章“有限温度量子多体系统与热态张量网络”(《物理》期刊2017 年第7 期)。在本节的后面部分中，作者重点介绍有限温度张量方法的若干最近发展。

A.有限温度张量网络

一维量子体系的配分函数计算可以表达为1+1 维的有限温度张量网络缩并问题。上世纪90 年代，我国学者向涛、王孝群等提出了转移矩阵重正化群(Transfer-Matrix Renormalization Group,TMRG)方法[17–19]，将模型的哈密顿量形式分为奇偶两部分H=Ho+He，其中奇数部分Ho= ∑i h2i-1,2i，偶数部分He=随后，利用Trotter-Suzuki 分解[37,38]将倒温度β分为M个较小的Trotter 切片并通过插入2M -1 组正交归一基，可以进一步得到：

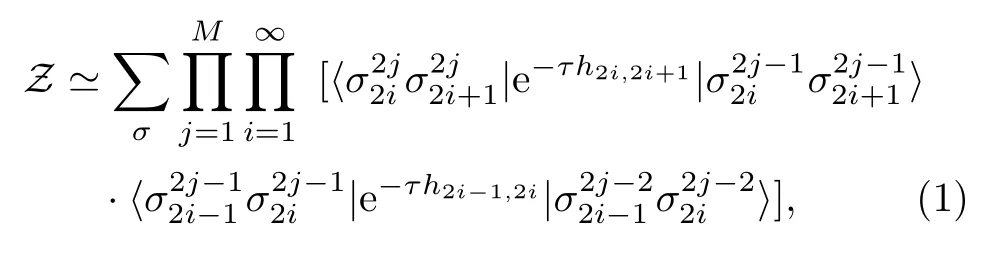
式中j标记倒温度空间，i标记实空间，在二维平面上可以形象地表示为图1(c) 所示的1+1 维张量网络。

在TMRG 方法中，系统自由能可以由转移矩阵T(如图1(c) 中橙色虚线框中所示) 的最大本征值λmax给出，即在具体计算时，TMRG借鉴基态的实空间密度矩阵重正化群(Density Matrix Renormalization Group, DMRG) 计算方法，在倒温度空间(图1(c)中竖直方向)利用DMRG 方法计算T的最大本征值λmax[17–19]，并进而得到自由能等热力学性质。值得注意，最近人们将转移矩阵T写成连续(时间)MPO，去除了Trotter 分解带来的分立误差，并可以更为方便地研究系统的(虚时间) 动力学性质[39]。

另一种在细节有一定差别但实质等价的算法是线性张量重正化群(Linearized Tensor Renormalization Group, LTRG) 方法。图1(c) 展示了LTRG 方法的要点，该方法按如下方式缩并热态张量网络：通过虚时间演化沿着温度轴方向缩并有限温度张量网络，得到密度算符ρ(β) 的矩阵乘积算符表示(如图1(b) 所示)，随后求迹得到配分函数Z(β) 并计算自由能等热力学量。依此路线LTRG 方法可精确计算一维自旋系统以及部分二维系统的平衡态性质，更多细节请参照文献[20,22]。

类似地，在两维量子系统的精确模拟中，人们可以将两维热态表达成张量乘积算符(Tensor Product Operator,TPO)[20]的形式，然后进行虚时间演化、或者变分地去优化，这样的算法可以直接得到热力学极限下的性质[20,21,23,40–44]，但由于计算代价较高，所允许的保留态数目通常较小。目前，人们仍在努力探索,开发精确有效且高度可控的、适用于更具挑战性的阻挫量子自旋和费米子等系统的TPO 算法。近年来，作者与合作者通过将二维系统映射为准一维系统，发展出了级数展开热张量网络方法(Series-Expansion Thermal Tensor Network, SETTN)[27]，并在此基础上进一步提出指数张量重正化群方法(Exponential Thermal Renormalization Group, XTRG)[28,31]等，可以精准、可控地处理一些其他方法难于处理的二维阻挫自旋系统[29,30,45,46]以及掺杂费米子[47]问题，展现出独特的优势及竞争力。

除了上面所提到的缩并热态张量网络的方案，有效计算两维系统有限温度性质的另一类张量网络态方法是最小纠缠典型热态法(Minimally Entangled Typical Thermal States, METTS)[25,26]。此方法将密度矩阵的计算问题转变为对典型热态的抽样问题，有效减小了所需的保留态数目，但也引入了统计误差。由于每个单独典型热态的制备需要开展DMRG 计算虚时间演化，且实际需要大量的典型热态做统计平均，因此METTS 方法具有较大的计算代价。该方法在量子自旋模型的研究上也有一些初步应用[48]。

B.指数张量重正化群

近期，人们尝试运用矩阵乘积算符来表达二维有限尺寸系统的密度矩阵，并取得了系列进展。图2 中介绍了XTRG 方法的主要路线：两维有限尺寸系统的密度矩阵ρ(β)≡e-βH(此处未归一化) 可以写作矩阵乘积算符的准一维形式，初始倒温度τ对应的ρ(τ) 可以通过泰勒展开表示为

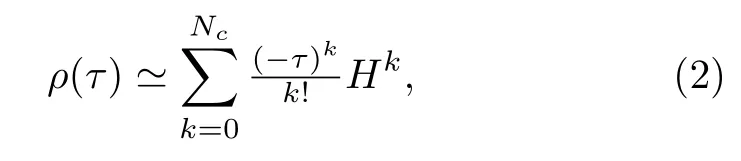
其中Nc是裁剪阶数，得到该密度矩阵ρ(τ) 张量网络表示的算法被作者称为SETTN[27]。此后，在每一步迭代降温过程中，采用XTRG 方法，即

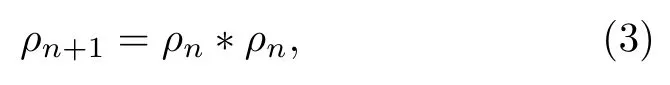
此处的“*”表示矩阵乘积算符的乘法运算。利用这样的机制，成倍增加倒温度β，即对应每一次迭代n，密度矩阵ρn所对应的倒温度β= 2n ·τ(见图2(b) 所示)，可以使系统迅速地将温度降低至低温区域。此外，在密度矩阵乘积算符进行压缩、截断时，XTRG 方法应用变分优化的策略，使计算复杂度保证在O(D4)的量级[28]。由于单次XTRG 演化所得到的温度点较为稀疏，作者通过引入平移系数z ∈[0,1) 来改变初始的τ →2zτ，多任务并行得到交替(Interleaved)的计算数据，有效提高了数据的温度分辨率[28]。

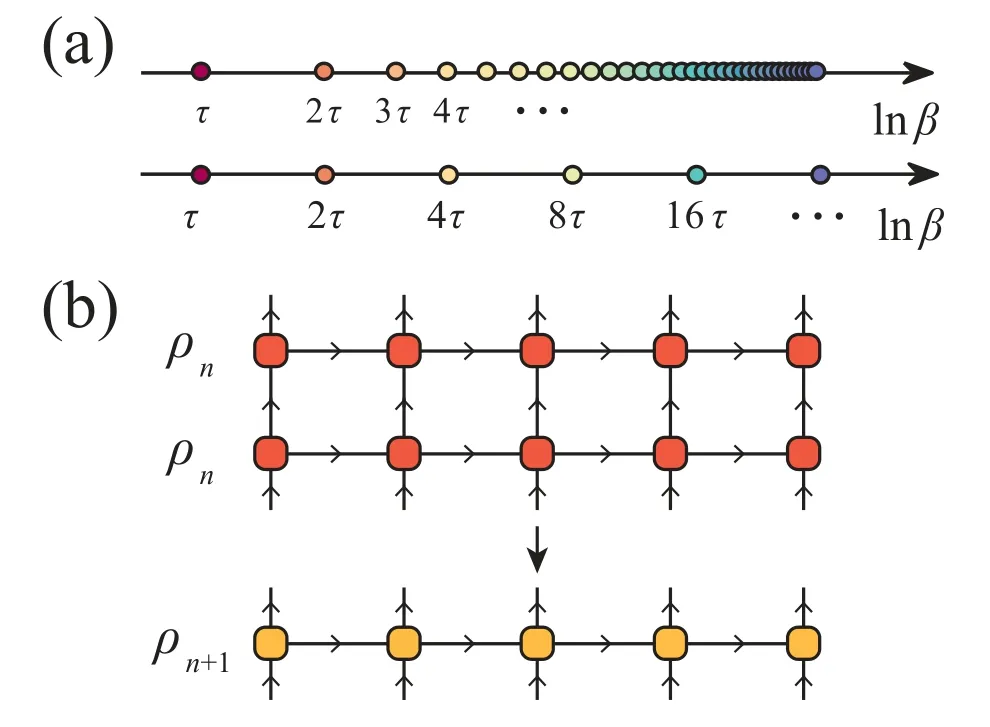
图2.(a) 有限温度多体计算中的线性和对数温度标度。(b)XTRG 演化的具体步骤：将温度为β = 2nτ 处的密度矩阵ρn 与自身相乘得到下一温度点的密度矩阵ρn+1。其中，竖线表示物理空间指标，横线表示几何或键空间指标。箭头流入(流出) 方向标记狄拉克右(左) 矢态空间。(引自文献[28] 图2)

最后，虽然XTRG 通过指数降温减小了累积误差，但与LTRG 一样仍不可避免存在截断误差随温度下降不断累积的问题。为了进一步提高计算精度，在最近的工作中，作者与合作者针对具体的温度优化系统自由能，借鉴机器学习中的自动微分编程思想，成功实现了温度方向的扫描，称为可微张量重正化群(∂TRG)[31]，较XTRG 相比进一步改善了计算精度。

上述各类算法从多体计算角度为研究两维量子自旋系统打开了大门，作者期待这类多体模拟算法可以与其它领域交叉、融合，不断提高计算精度与效率，完善量子多体系统的“武器库”，用以研究阻挫磁性等强关联物理的重要前沿问题。

C.正方晶格海森堡模型的有限温度张量重正化群计算

在介绍具体阻挫量子磁体及其材料体系研究之前，作者首先介绍指数张量重正化群方法XTRG 在正方[30]和三角晶格海森堡模型热力学性质研究中的应用[29]，以此展示有限温度张量方法在加深人们对量子磁性模型理解方面的作用。

在图3 中，作者固定系统尺寸为OSL×L(其中L从4 增大到10)，利用低温下布里渊区中M 点的结构因子计算出了正方晶格反铁磁海森堡模型的自发磁矩作者展示出自发磁矩对温度的依赖关系，发现不同尺寸下的曲线会在温度T≲0.1处趋于定值，大小随温度降低而收敛。在图3 的插图中，作者将这些定值的平方m2(L) 对1/L进行二次型外推[49]，得到自发磁矩m* ≃0.30(1)，与QMC 计算所得结果m ≃0.307 0(2)[49]十分相符。

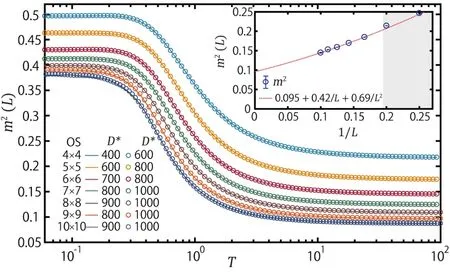
图3.正方晶格海森堡模型的磁矩曲线(D* 是保留的多重态数目)，其中系统尺寸固定为OS L×L，L ≤10(两个方向均为开边界)。插图展示了温度为T = 0.1 时的m2(L) 的值及其二次型拟合结果(图中灰色区域中的小尺寸结果没有被采用)。(引自文献[30] 图8)

除此之外，作者也对正方晶格横场伊辛模型进行了研究，采用XTRG 算法精确确定相变温度Tc。根据有限尺寸标度(Finite-Size Scaling, FSS) 理论，高阶矩可以用于有效地确定相变温度，如宾德尔比率(Binder Ratio)U4，其受有限尺寸效应的影响较小，不同系统尺寸下的U4值会在相变温度Tc处相交。在XTRG 方法中，高阶矩如U4等也便于计算：因为总自旋算符Sztot可以被写作键维度D= 2 的简单的MPO 形式，由此可以方便的构造出(Sztot)2(D=3)和(Sztot)4(D=5)的MPO 表示。在图4 中，作者利用XTRG 及QMC 方法计算了磁有序相里正方晶格横场伊辛模型的宾德尔比率，发现两种方法得到的结果完全吻合。通过把宽度为W+1 及W的两条曲线交点处的温度记为临界温度T*c(W)，并对1/W2→0 进行外推，得到临界温度T*c≃0.421 2，其与热力学极限下的结果[23]相对误差小于0.6 %。

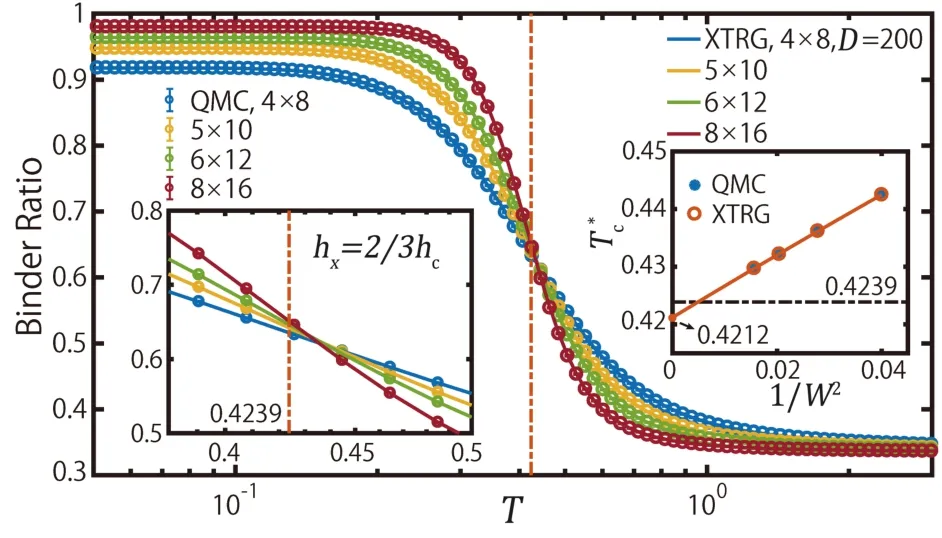
图4.正方晶格横场伊辛模型在hx = hc(hc 为模型磁有序–无序量子相变的临界场) 时的宾德尔比率曲线，系统尺寸为YC W ×2W(沿着宽度方向周期边界条件、长度方向开边界条件的系统) 。左侧插图是对临界温度 处结果的放大；右侧插图是相变温度 对1/W2 →0 的二阶多项式拟合。(引自文献[30] 图12)

D.阻挫三角格子海森堡模型的有限温度张量重正化群计算

三角晶格海森堡(TLH) 模型是最典型的阻挫量子自旋系统之一。自从1973 年P.Anderson 在三角晶格上提出著名的共振价键态(RVB) 理论后[7]，TLH 模型的基态是RVB 自旋液体，还是半经典的磁有序相，成为人们长期热烈讨论的问题[50–57]。目前人们广泛认为TLH 模型的基态是非共线的120°序，自发磁矩m ≃0.205[53,54]。然而，在研究其有限温度性质时，人们却发现了一些反常：TLH 系统直至很低温度都没有进入人们预期的初期磁有序(Incipient Spin Order)区[58]，甚至一些研究表明从有限温度外推到零温得到了磁无序基态[56]。这些看似矛盾的结论，其症结在于大尺寸磁阻挫系统低温性质精确计算方法的缺失。

作者利用所发展的XTRG 方法开展了三角晶格反铁磁海森堡模型热力学性质的研究。在图5(a)中，作者发现比热容展现出双峰结构：即在高温温度尺度Th≃0.55J处(J是最近邻反铁磁耦合系数)，比热容会呈现出圆峰；而在低温尺度Tl≃0.2J处，比热容还会展现出另一个峰/肩膀。随着尺寸增大，作者观察到低温峰的高度会逐渐降低，但特征温度Tl十分稳定，并不随系统宽度W的变化而移动。

在图5(a) 中，作者还给出了新近合成的三角晶格材料Ba8CoNb6O24(BCNO) 的实验测量结果[59,60]，并进行对照。BCNO 是一类钙钛矿材料，其中的Co2+离子在二维平面形成自旋1/2 的三角晶格结构，常规热力学及核磁共振谱学探测在温度降至0.06-0.1 K 时，都没有探测到长程磁有序及自旋的各向异性，此前研究认为BCNO 材料实现了三角晶格上各向同性的海森堡模型[59,60]。在图5(a)中，作者将计算结果与BCNO 的实验数据进行对比，按照实验能标，将相互作用J值定为1.66 K 左右，发现在T≳Th时，XTRG、TPO、高温级数展开(High-Temperature Series Expansion, HTSE)[61]，和Padé 近似[60]得到的结果都与实验符合得很好，并且可以重复出比热容在高温特征温度Th处的圆峰行为。值得指出，由于XTRG 可以精确计算系统到比其他方法更低的温度，并得到比热容的低温特征温度Tl，与实验观察到的行为非常一致，从而确认了三角晶格海森堡模型的双温标行为。这一结论也被最近的三角晶格阻挫磁体实验[62]和其他有限温度计算研究[63]所支持。

基于上述热力学计算结果，作者提出TLH 模型中存在双温度尺度现象，其有限温度相图如图5(b) 所示。在温度T ＜Tl时，作者在左侧部分画出了初期120°序；在温度T ＞Th时，作者在右侧部分画出了高温顺磁自旋构型示意图；而当温度居于两尺度之间时，作者发现一中间区域，且只通过基态的120°序及K 点附近磁振子激发，并不足以描述该模型中的双温标特征。在文献[64,65]中，研究者们提出TLH 模型中还存在另一项有能隙的激发，其平方型色散图景和He4超流体系中的涡旋型激发十分相像，因此人们将其称为“类旋子激发”(Roton-like Excitations, RLEs)。人们利用中子散射实验[66,67]，也在一些三角晶格量子反铁磁材料中观察到了RLEs 激发。结合中间温度区间的手征关联〈χiχj〉β的反常增强(其中手征算符χ ≡23·[Sa ·(Sb × Sc)]，(a,b,c) 分别表示同一个三角形的三个格点)，作者提出正是RLEs 激发导致了TLH 系统的双温标现象[29]。

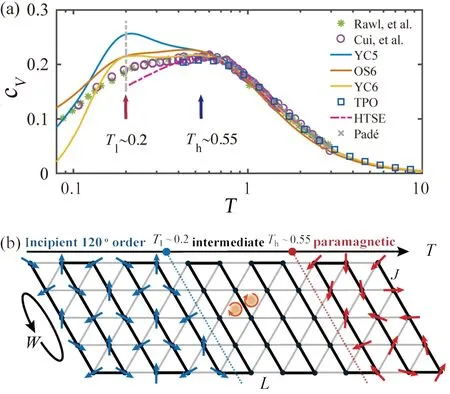
图5.(a) 采用不同数值计算方法与两个独立实验比热容cV测量结果的直接对照[59,60]。在XTRG 计算中，系统尺寸采用YC 及OS 两种，张量乘积算符(TPO) 算法计算了无穷大系统的结果，其中HTSE 和Padé 近似的结果来自文献[60,61]。(b) 三角晶格示意图，左、中、右分别表示低、中间及高温区域，以温度尺度Tl 和Th 隔开。图中的黑色粗线表示XTRG算法采用的“蛇形”准一维映射路径。在中间温区，顺时针朝向的圆形标记表示手征关联的反常增强。(改编自文献[29] 图1 与图2)

上述研究结果表明，XTRG 方法在模拟二维格点系统的有限温度性质时是精确且高效的。相比基态DMRG 方法，有限温度XTRG 可以研究各种序之间的竞争、探讨系统在降温过程中如何演化到基态，且在一定的温度窗口中受有限尺寸效应影响较小。此外，基态DMRG 研究的是个别态(基态和若干低能激发态) 的性质，而XTRG 计算有限温度性质将态密度的信息也自然地包括进去了，更集中反映了相的性质。最后，XTRG可以计算比热容、磁化率等热力学测量数据，与实验有更为丰富的联系。在下一节中，作者将XTRG 方法应用于实际阻挫量子自旋系统与材料的研究中，对其中的量子物相展开深入探讨。

III.三角晶格阻挫磁体及BEREZINSKII -KOSTERLITZ - THOULESS 相变

近年来，在探索三角晶格自旋液体态与其候选材料时，人们对稀土磁体 YbMgGaO4及其中可能的自旋液体态产生了浓厚的研究兴趣[68–73]。人们发现，YbMgGaO4在温度降低至30 mK 时都没有形成长程磁序[71]，而这一温度较之所估计的反铁磁相互作用能标4 K[68,69]相差两个量级；同时，中子散射探测到了连续谱形式[71,73]，表明YbMgGaO4展现出了自旋液体的特征。然而，该材料中的Mg2+、Ga3+存在占位无序[74]，一些研究也指出自旋液体特征或许为无序效应的反映[75,76]。

最近，人们将YbMgGaO4中的Yb3+替换为Tm3+离子，制备得到TmMgGaO4(TMGO) 单晶样品[77–79]。通过低温中子散射实验，人们观察到TMGO 的基态是磁有序的而非自旋液体。作者及合作者利用XTRG 等方法，揭示TMGO 的精确微观模型，探讨了该阻挫磁性材料中的演生U(1) 对称与BKT 拓扑相变。

根据Mermin-Wagner 定理，具有连续对称性的二维相互作用体系，自发对称性破缺会在有限温度被恢复[80]，因而这类系统中不会发生有限温度相变。然而，若系统存在具有非平庸拓扑特征的涡旋激发，则可以经历从有准长程序相到高温无序相的相变[3,81]。即在低温时，涡旋与反涡旋两两配对，被束缚在一起，不易被散射，故体系不存在耗散，展现出超流特性，关联函数代数衰减；而在高温区域，由于热涨落很强，涡旋对会解束缚而形成自由运动的孤立涡旋，容易受到散射改变位形并导致耗散，此时系统不具有长程相位有序，关联函数指数衰减。如图6 所示，在温度为TBKT处系统发生从低温准长程序到高温无序的相变，这一相变不是由对称破缺驱动的，而是由涡旋–反涡旋对的束缚与解束缚而驱动的，是为BKT 拓扑相变。值得注意的是，BKT相变不仅仅可以在显式具有XY (或U(1)) 对称性的模型中出现，在阻挫自旋模型中存在演生U(1) 对称性时，同样也可以出现BKT 相变。

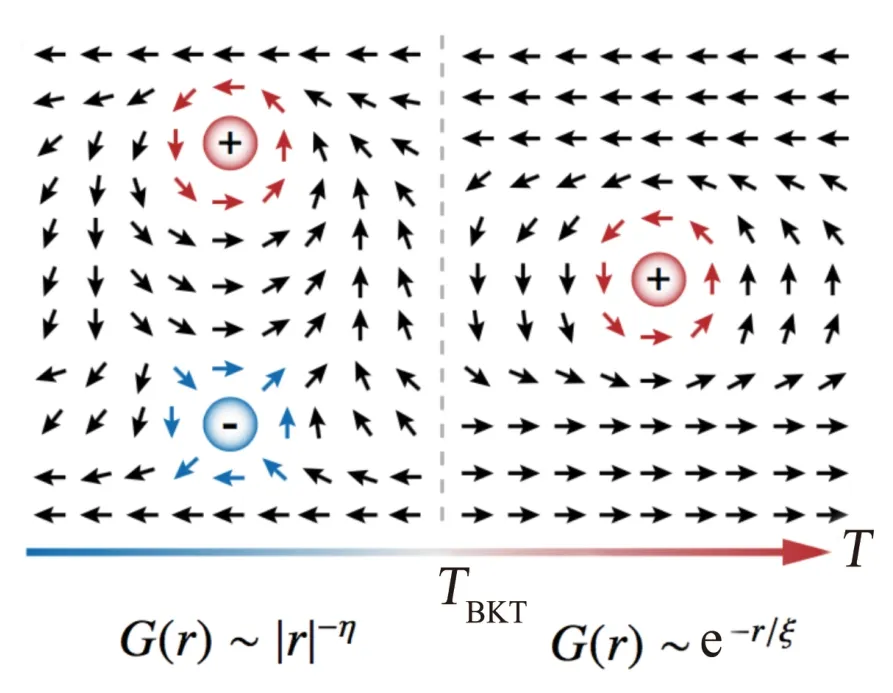
图6.二维XY 模型当温度升高至TBKT =πJ/2KB (J 为自旋耦合强度) 时，由于系统中涡旋–反涡旋对解耦，发散涡旋数目激增，驱动BKT 拓扑相变。G(r) 为自旋关联函数随距离r 的关系，η 为幂率指数，ξ 为关联长度。

A.阻挫伊辛磁体TmMgGaO4 的微观自旋模型

TMGO 晶体中的稀土离子Tm3+处于氧的八面体晶体场中，存在两个近简并的基态能级(构成非克拉默双重态)，因此每个Tm3+可以视为有效自旋1/2。同时，第一性原理计算表明O2-离子的2p 电子会形成超交换轨道，使得Tm3+离子的4f12电子在层内产生耦合，在二维平面形成三角晶格结构(如图7(a)所示)，且层间耦合十分微弱。

最初人们认为TMGO 材料可以被三角晶格经典伊辛模型所描述；随后，非弹性中子散射(INS) 实验的结果揭示出系统存在十分清晰的自旋波激发谱[79]，表明系统存在与伊辛耦合不对易的相互作用项，为量子伊辛磁体。进一步的分析指出，由于Tm3+离子总角动量J= 6，不满足克拉默定理，因此晶体场的最低准双重态|Φ±〉间应存在一个小的能级劈裂Δ，可以理解为内秉的横场项[82]。由此，TMGO 反铁磁体的有效哈密顿量可以写为[79]：

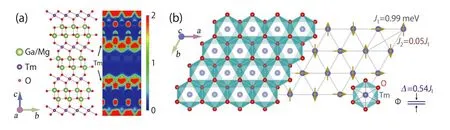
图7.(a) 晶格结构及部分电子密度ρe 的侧视图，其中两层Tm3+ 之间的ρe 比处于超交换轨道间的ρe 要低2-3 个数量级，显示出很好的二维磁性。(b) 处于三角晶格格点位置处的Tm3+ 离子，会在氧离子所形成的八面体晶体场中发生能级劈裂，对应的两个非克拉默简并的最低能级|Φ±〉 间有大小为Δ 的能隙，其低能有效模型为三角晶格上的自旋1/2 模型(J1 和J2 分别为最近邻和次近邻相互作用)。在低温“钟态”反铁磁序中，作者画出了其自旋指向的示意图，其中竖直方向表示材料的各向异性易轴c 轴方向，朝上或朝下的暗黄色箭头表示自旋向上或自旋向下，水平箭头表示自旋朝上和朝下的叠加态| →〉。(改编自文献[45] 图1 及其附录图1)

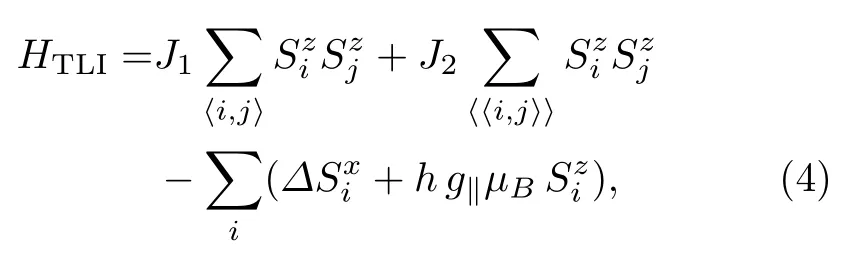
其中，〈,〉(〈〈,〉〉)表示最近邻(次近邻)相互作用J1(J2)，Δ为|Φ±〉间的能级劈裂(即内禀横场)，h为沿c轴的外加磁场项(如图7(b) 所示)。g‖=2JgJ(J=6) 是有效自旋1/2 的g因子，其中gJ为朗德因子。

基于式(4) 中的三角量子伊辛哈密顿量，作者采用XTRG 计算了比热容、热力学熵、磁化率、磁化曲线等磁热力学量并调节参数与实验进行了定量拟合[78,79]，确定采用同一套参数(J1= 0.99 meV，J2= 0.05J1，Δ=0.54J1，g‖ ≃13.2)，可以同时精确拟合上述多个实验测量结果。在图8(a) 中，当温度较高(T ＞30 K) 时，热力学熵Sm十分接近Rln2，对应有效自旋1/2 系统的高温顺磁相；当温度降低时，Sm逐渐减小，系统形成低温反铁磁序(如图7(b) 所示)[79]。在图8(b,c) 中，模型计算可以定量复现比热容曲线cm(包括圆峰结构的位置与高度等) 以及磁化率曲线的两次上升。在相当宽的温度区间(从30-100 K 降温到1 K)，模型计算曲线都与实验结果高度吻合，因此可以从热力学测量上反推确定TMGO 磁体的微观自旋模型为三角横场伊辛模型。

为了验证这一模型的精确性和有效性，作者开展中间温度(2 K) 和极低温(40-60 mK) 的磁化曲线M(h)计算，将XTRG 多体计算结果与实验曲线进行对比(此时不再对模型参数做调整)。结果如图8(d) 所示，作者观察到磁化曲线高度吻合。值得注意的是，实验上观察到磁化曲线在20-25 kOe 处会发生行为的变化，这一变化随着温度T的降低而愈发明显(见图8(d) 的插图)，表明在2.5 T 左右存在磁场诱导的量子相变，后续模型计算也证实了这一点[83]。

TMGO 晶体中子谱学探测的结果也可以通过该微观模型(式(4)所示)加以定量解释。通过QMC-SAC 方法[84–88]计算得到动力学结构因子S(q,ω)，作者发现所得结果与非弹性中子散射的测量结果[79]完美符合，如图9 所示。特别是计算结果表明系统在M 点打开了约为0.4 meV 的能隙，也与文献[79]中的实验报道结果定量符合。综上，通过热力学与动力学结果的多体计算与分析，作者确定了阻挫量子伊辛磁体TMGO 的精确微观模型及相互作用参数，为讨论其中的新奇物态与相变提供了坚实的基础。

B.赝自旋映射与演生U(1) 对称性

BKT 相变是由U(1) 相位场中的涡旋激发所驱动的无穷阶拓扑相变，对于此处的TMGO 三角晶格伊辛系统，哈密顿量(式(4) 所示) 中并不直接具有这样的对称性，但其可以在系统中自发地涌现出来。这一发现最早是由Moessner 等人在阻挫三角晶格量子伊辛模型的研究中所提出的，即量子临界点存在演生U(1) 并在有限温度扩展到一中间相[6]。具体地说，在三角晶格自旋模型中引入如下赝自旋映射，即

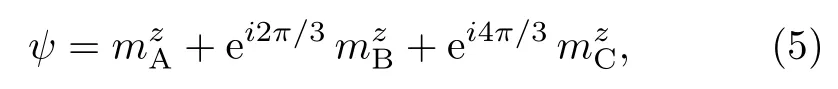
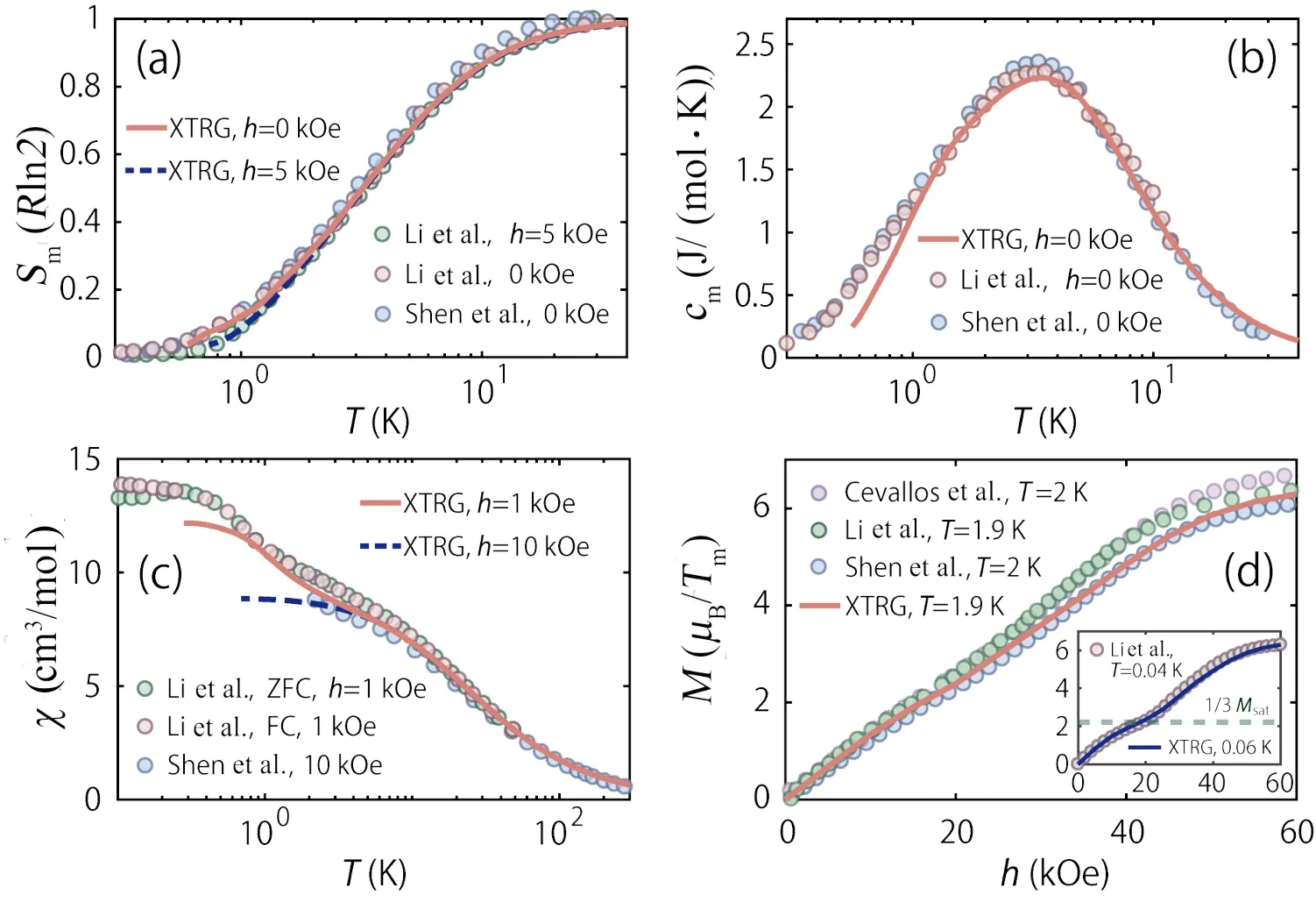
图8.热力学多体计算数据与实验结果[77-79] 的拟合情况。(a) 磁场h=0 及5 kOe 处的热力学熵曲线[78,79]，(b) 零场比热容数据，(c) 磁化率，(d) 中间温度及低温下的磁化曲线。(改编自文献[45] 图2)

其中ψ=meiθ为一复数序参量[89]，幅值为m，相角为θ；A、B、C 标记晶格的三个子格。如图10 所示，对于每一种磁构型，人们均可以计算出每一个三角形对应的ψ，并将其标记在三角形中心，幅角场θ即构成BKT物理相关的相位场。

通过式(5) 的映射关系，人们建立起了三角晶格横场伊辛模型的LGW 理论，相应的有效哈密顿量为[90]

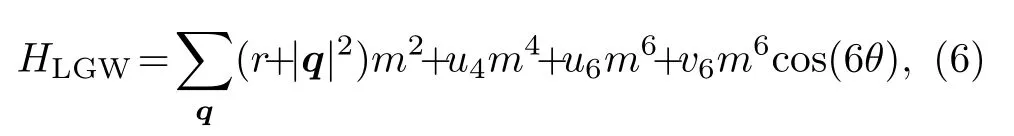
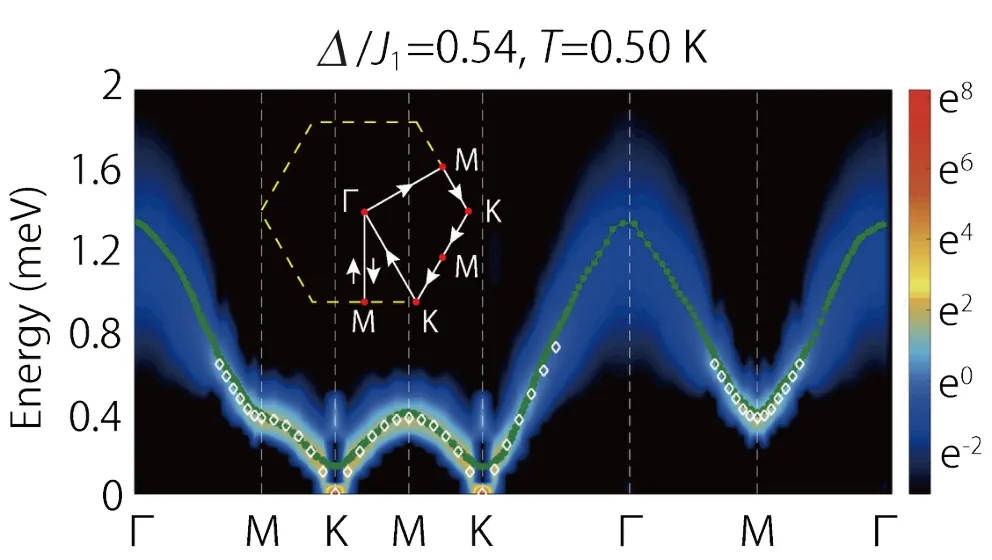
图9.温度为T = 0.5 K 时，根据正文所述模型参数，利用QMC-SAC 方法计算得到的能谱，计算结果与文献[79] 中的非弹性中子散射结果(图中的绿色点线) 一致。(引自文献[45]图4)

当横场项在量子相变点左侧时(如图10(c) 所示)，在低温下序参量的幅值m和系数v6都是有限值[89]，因此有效哈密顿量依赖于v6m6cos(6θ) 项，系统具有分立对称性。由于“无序生有序”(order by disorder)效应，此时系统的基态为六重简并的三子格反铁磁序，在赝自旋复平面上构成同一圆上的六个对称点(如图10(a) 中的红色圆点)[89]，对应幅角θ=(2n+1)π/6(其中n=0、1、2···5)，赝自旋自发破缺六重对称性，如图10(b) 所示，因此也被称为六态钟有序(6-state clock order)。钟态模型实际上为一种分立形式的XY 模型，随着升高温度，六态钟有序反铁磁相会经历两步“融化”，均为BKT类型。在两次相变中间，各向异性项(即公式(6) 中的cos(6θ)项)为高阶无关微扰，有效哈密顿量只依赖于幅值m，系统由此具有演生U(1) 对称性[6,91]。

综上，按照所确定的微观模型，作者预言TMGO材料在降温过程中会涌现出哈密顿量中原本不具备的U(1)对称性，并经历两次BKT 拓扑相变最终进入钟态有序。由于BKT 相变的特点，这一磁有序的产生并不伴随有比热容或磁化率的发散峰，从实验上探测TMGO中的BKT 相变需要其他手段。

C.低温热力学及谱学实验证实

核磁共振实验可以非常灵敏的探测低能自旋涨落[92–95]。在图11中，作者与合作者开展TMGO 晶体中的自旋–晶格弛豫率1/T1测量，借以考察理论预言的BKT 相变。作者展示了面内磁场μ0H=1 T 及3 T 时1/69T1随温度的变化，如图11(a) 所示，反映出材料的本征自旋涨落。系统从10 K 开始降温时，1/69T1随温度下降而减小，但是当降温至1.9 K 时反常增大，表明此时系统中有很强的低能自旋涨落；当温度Tl≃0.9 K时，1/69T1的值会迅速减小，此时系统主要被有序相中的有能隙的长波激发所主导，这与从超精细位移结果中推测出的长程磁有序建立的温度是一致的[96]。通常而言，在相变点处，由于关联长度发散，系统中会有大量无能隙的低能自旋涨落，因此1/T1会出现峰值。而作者注意到，当温度处于1.9 和0.9 K 之间时，1/69T1会展现出类似平台的结构，表明在中间温区中，系统会进入到一个拥有很强涨落的中间相，该相中自旋关联是发散的，却没有建立起真正的长程序，这与BKT 相的特点相符合。在图11(b)中，作者发现应用QMC-SAC 方法计算得到的TMGO 模型的1/T1与实验测量结果十分一致，两个特征温度及中间温区准平台形状的特征与实验曲线高度符合。

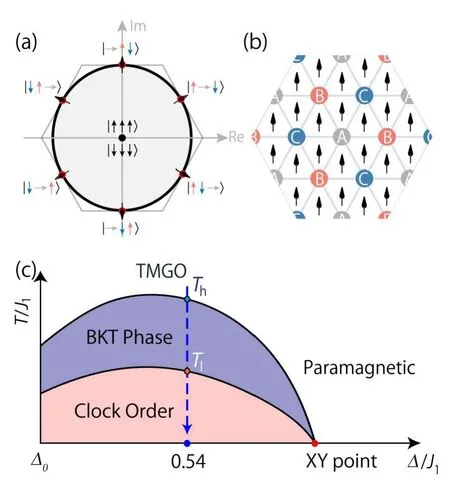
图10.(a) 三角晶格磁有序态及其复平面赝自旋序参量对应(式(5))。所得复数序参量ψ 在图中用面内旋转的箭头来表示其幅角。(b) 赝自旋映射下的“钟态”反铁磁序示意图，红色格点表示自旋向上(mz = 1/2)，蓝色格点表示自旋向下(mz =-1/2)，灰色格点表示叠加态|→〉(mz =0)。(c) 三角晶格横场伊辛模型的有限温度相图(示意图)。

从TMGO 磁化率测量的标度行为上，也能观察到BKT 相变的证据。在图12 中，作者展示了面外磁场下的微分磁化率dM/dH的曲线。场论分析表明三角晶格反铁磁量子伊辛系统在处于BKT 相时，磁化率会呈现出反常的普适发散行为：χ(h)=h-α，其中且当温度T=Tl, 对应χ(h)～h-2/3，磁化率会随着磁场趋近于零而逐渐发散；当温度等于Th，对应磁化率随磁场变化始终为一定值。据此，在图12(a) 中，作者对不同温度下的dM/dH的数据进行了代数拟合，发现当温度为0.8 K 以下时，α的值非常接近理论上限2/3(即η=1/9)；当温度升至3 K 及以上时，α会减小到接近于零(η=2/9)。基于上文提到的TMGO 有效模型，作者也利用QMC 方法计算了相应温度下的磁化率数据，并将其展示在图12(b) 中，与实验结果进行对比。当温度小于等于0.8 K 时，拟合得到的α ≃2/3，与实验结果十分一致。通过观察到普适的磁化率代数发散行为，作者提供了材料中存在BKT 相变的另一重要证据。

最近，佐治亚理工大学等联合实验团队设计了中子散射实验[99]，验证了TMGO 在有限温度上存在BKT相变，并通过确定TMGO 模型中的首要项，支持了上述有效模型的正确性；在文献[82,83,100]中，人们讨论了面外场下的有限温度相图；在文献[78,99]中，研究者们讨论了材料中由于Mg/Ga 占位无序带来的随机内禀横场效应等。因此，关于TMGO 材料中的新奇量子磁性物态与相变等更多问题仍然值得后续深入探讨。

IV.六角晶格KITAEV 阻挫磁体及高场自旋液体相

六角晶格Kitaev 模型提供了人们认识自旋液体态的严格可解范例[11]。在Kitaev 自旋液体态中，自旋激发会分数化为巡游及局域的马约拉纳费米子激发，是研究自旋液体的典型系统[11,101]。如果引入破缺时间反演对称性的微扰(如磁场) 项，系统会进入到有能隙的手征自旋液体相，存在非阿贝尔任意子激发，在拓扑量子计算[11,102]等领域有潜在的应用前景。

最近的研究进展表明，Kitaev 阻挫自旋模型可以在若干候选材料体系中被实现，一些代表性的磁性材料包括α-RuCl3[103–107]，铱氧化物Na2IrO3[103,105,108–111]和Li2IrO3[111–115]等，其中的4d 或5d 电子能级在晶体场中发生劈裂，并在自旋–轨道耦合作用下带来有效角动量jeff=1/2。根据2009 年Jackeli 和Khaliullin 所提出的机制[103]，由于自旋轨道耦合和特殊的键角关系，这类材料有效自旋之间的海森堡相互作用被抑制，可能实现Kitaev 相互作用主导的量子磁性系统。

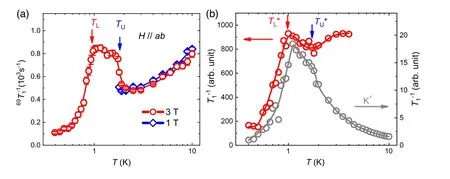
图11.(a) 在面内磁场为3 T 及1 T 时，核磁共振测量得到的自旋–晶格弛豫率1/69T1。(b) 通过动力学自旋关联函数计算得到的1/T1。其中红色曲线和灰色曲线分别为考虑所有动量点的贡献及只考虑K 点附近的动量点的贡献时的计算结果。(引自文献[96]图2)

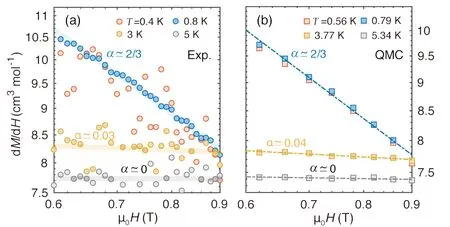
图12.TmMgGaO4 的磁化率及标度行为分析。(a) 实验测得的dM/dH 结果，(b) 微观自旋模型计算结果。通过代数拟合dM/dH ～H-α，作者得到理论预期的BKT 相变临界指数。

A.六角晶格Kitaev 模型

2006 年，Kitaev 提出六角晶格严格可解的自旋液体模型[11]，这一模型(后文简称为Kitaev 模型) 的哈密顿量为

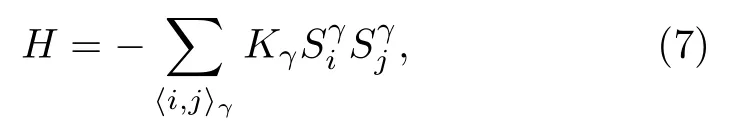
其中〈i,j〉γ表示最近邻γ=(x、y、z) 类型的键上的相互作用，并对所有最近邻键求和。由于每一个格点的自旋与其最近邻γ= (x, y, z) 的自旋存在不同方向的伊辛型相互作用Kγ，如图13(a) 所示，系统中会存在很强的自旋阻挫，并导致系统在基态进入Kitaev 自旋液体态。

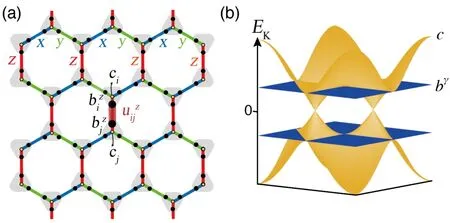
图13.(a) 六角晶格上的Kitaev 模型，其中(x, y, z) 表示三种伊辛类型的相互作用键，分别用蓝、绿、红色表示；马约拉纳费米子算符如黑色及黄色圆点所示(bzi、bzj、ci、cj 等)；自旋算符如灰色三角形所示；局域的z 类型的键算符uij 如深红色粗线段所示。(b) 巡游的c 及局域的bγ 马约拉纳费米子的色散关系。此处展示的是Kitaev 相互作用Kx =Ky =Kz的情况。

在 Kitaev 模型中，自旋自由度可以被分数化的马约拉纳费米子 (电中性，反粒子为其本身) 所有效表示，即将自旋来替换，如图 13(a)所示。这里和cj表示四种马约拉纳模式，并且满足约束条件因此哈密顿量可以写为其中的局域键算符与哈密顿量是对易的，且满足这样的键算符uij绕着六边形乘在一起构成Wp(其中i、j、k、l、m、n标记一个六边形p的六个顶点，见图14(d)插图)，并与哈密顿量对易，是本征值为±1 的Z2规范通量。因此，Kitaev模型可以被无穷多个局域的守恒量所刻画，其基态为一种Z2量子自旋液体，也被称为Kitaev 自旋液体(Kitaev spin liquid, KSL)。除基态性质之外，Kitaev 模型的有限温度性质也可以通过马约拉纳表象下的蒙特卡洛方法进行计算[116–118]，人们发现系统存在热分数化(thermal fractionalization) 等新奇现象[116–120]。

目前人们认为，已有的典型 Kitaev 候选材料(如Na2IrO3及α-RuCl3) 中存在除Kitaev 相互作用(Kγ)[105,121–125]之外的Γ项[126,127]与海森堡相互作用J[121,128]，这些项也可能起到了重要的作用。然而，包含这样的非Kitaev 相互作用及磁场项[107,129]的扩展Kitaev 模型无法进行解析求解，且适用于原始Kitaev 模型的蒙特卡洛方法也会遇到“负符号问题”无法开展大尺寸和低温计算[124]。因此，在这样的扩展Kitaev 模型中，是否存在自旋液体相，其有限温度上是否还存在自旋的分数化，对实际Kitaev 材料研究有何启示，都是值得探讨的重要问题。

B.有限磁场下的Kitaev 模型与分数液体

指数张量重正化群XTRG 方法可以对阻挫Kitaev自旋模型开展精确多体计算研究。在图14 中，作者首先展示零磁场下的Kitaev 模型的比热容cV，热力学熵S/ln 2，和规范通量Wp的结果，并与此前的大尺寸量子蒙特卡罗计算结果进行直接对比[131]，揭示了有限温度上的双温度尺度行为(如图14 中的竖直虚线所示)。当系统温度降低时，Kitaev 模型在有限温度上会历经高温顺磁相、中间温区分数液体相和低温自旋液体相，这样的三个相被两个温度尺度TL和TH隔开。在图14(a)中，比热容在双温度尺度处呈现峰值；而熵在两温度尺度附近快速下降，分别释放掉的磁熵，并在中间温区——分数液体相中—— 展现出熵的分数准平台结构(如图14(b) 所示)；在图14(c) 和(d) 中，作者进一步展示了键自旋关联和规范通量Wp观测值分别在高温温度尺度(TH)和低温温度尺度(TL)附近建立起来。这一图像说明巡游马约拉纳自由度和Z2规范自由度各自携带了一半的熵，在不同的温度释放出来，发生了热分数化[131]。由于Kitaev 模型的高温(TH) 和低温温度尺度(TL) 相差较大，需要计算到极低温性质才能观察到TL附近的行为，作者新近发展的有限温度XTRG 方法具有独特的效率和精度优势。

以下考虑外磁场中的 Kitaev 模型，其哈密顿量

为了刻画中间分数液体的磁学性质，作者对均匀磁化率χ进行计算，发现其在中间温区展现出演生的居里行为，结果如图16 所示。这一普适行为有别于高温居里定律，是Kitaev 相互作用和规范场的涨落带来的演生居里行为，并延伸到整个分数液体区间，温区横跨一个数量级(T从约0.03 到约0.3)。在中间温区，演生的居里常数C′ ≈1/3，与高温顺磁居里行为存在显著不同(高温区的居里常数C=S(S+1)/3=1/4，其中S=1/2)，表明自旋关联已被建立并“重正化”了有效磁矩。

为了分析中间温区演生居里规律的起源，作者利用久保公式 (Kubo Formula)，并考虑有限温度分数液体相中不存在自发磁矩，将磁化率写为χ=

随后，利用莱曼谱表示对自旋关联进行展开，即

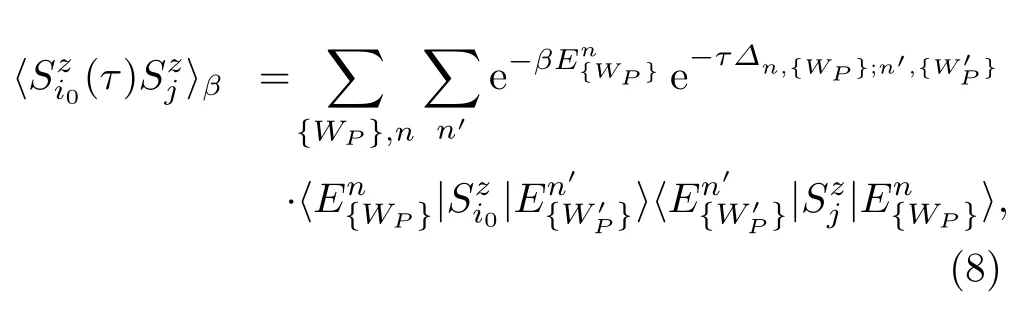
其中表示通量被翻转后的{W′P}构型中的n′态。假定激发能量Δn,{WP};n′,{W′P}主要由通量之间的激发能隙决定，则Δn,{WP};n′,{W′P}=因此，衰减因子e-τΔn,{WP};n′,{W′P} ≃1，表明在中间温区中实质上与τ无关。因此，当T≳TL时，磁化率可以简化为传统的表达式

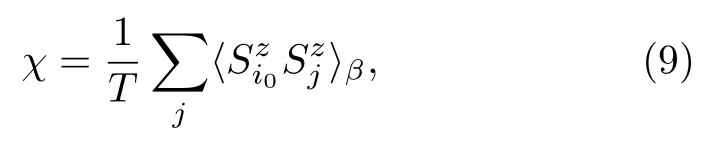
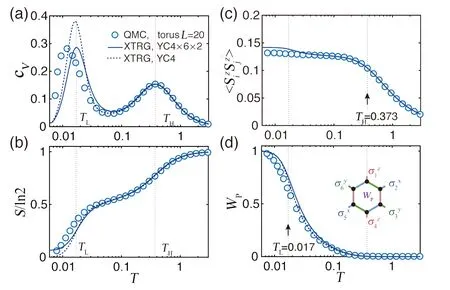
图14.六角晶格Kitaev 模型的有限温度性质计算结果，其中圆点表示边长为20 的环形面系统上的量子蒙特卡洛结果，实线和虚线表示XTRG 计算结果。(a)、(b)、(c)、(d) 分别为比热容曲线、熵曲线、z 类型键上的最近邻自旋关联〈Szi Szj〉 和通量Wp的计算结果。(改编自文献[130] 图10)

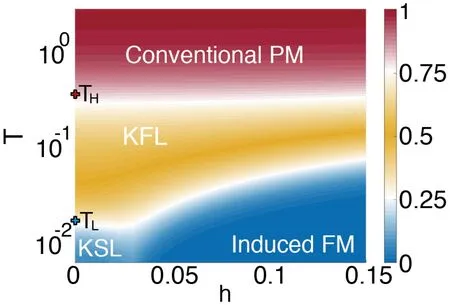
图15.有限磁场Kitaev 模型的等熵线(S/ln 2)，图中展示了两个温度尺度及中间温区的分数液体相。(改编自文献[130] 图3)

由于在分数液体中，系统只有极短程关联，此处的j只能取与格点i0以dz键相连的自旋；同时，由于关联值在中间温度展现出准平台特征，即近乎于一个常数(见图14(c) 所示)，因此在TL和TH之间磁化率χ ～1/T，呈现演生的居里行为。另一方面，在T≲TL时的KSL 相中，尽管关联仍然是极短程的，激发能量仍会导致一与τ有关的指数抑制因子存在。故而在温度TL以下，磁化率不再按照演生居里定律发散。

因此，在中间温区分数液体中，作者发现对于扩展Kitaev 模型仍然可以观察到磁化率的演生居里行为，这个普适行为直至系统降至更低温、建立起有限的通量能隙或自旋长程关联时才会终止，是Kitaev 模型及其扩展系统在有限温度的重要普适磁学特征。上述结果表明，对系统中的演生居里磁化率行为进行分析，也可以作为材料中是否存在Kitaev 相互作用的实验可测证据。更多其他扩展Kitaev 模型如Kitaev-Gamma、Kitaev-Heisenberg 等的结果请详见作者的最近工作[130]。

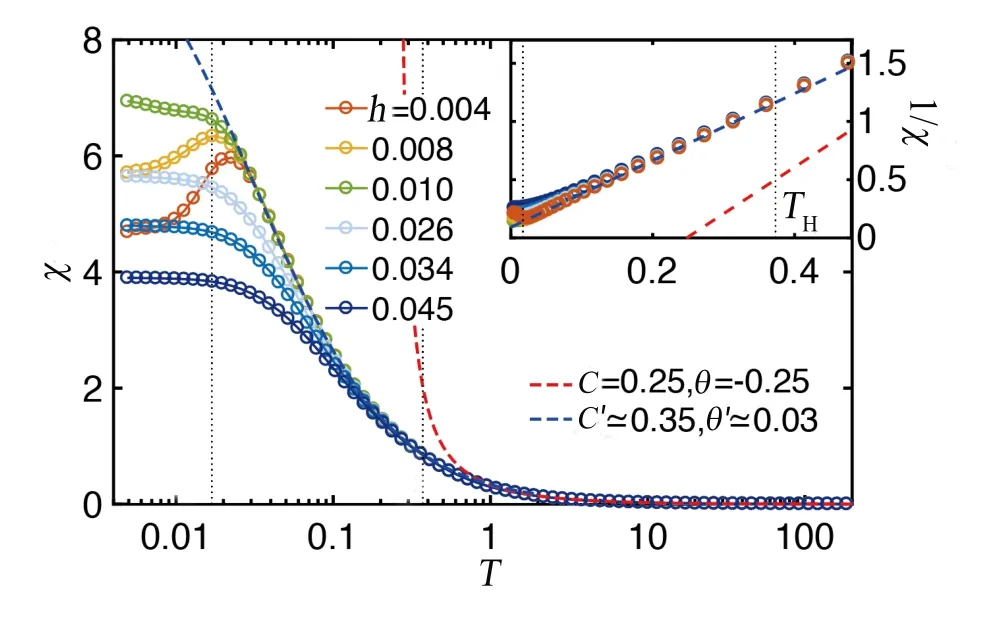
图16.不同磁场h 下的磁化率χ，其倒数1/χ 见插图。高温磁化率的行为符合居里–外斯定律1/(4T -J)，而当温度低于T ≃TH 时，磁化率存在演生居里定律行为。在高温和中间温区的不同居里行为分别如图中红色和蓝色虚线所示。(引自文献[130]图5)

C.Kitaev 候选材料α-RuCl3

实验上，人们观察到Kitaev 自旋液体候选材料α-RuCl3等在低温下(约为7 K 以下) 形成了“之字形”反铁磁序[122,135,138]，而非量子自旋液体，表明材料中还存在非Kitaev 类型的相互作用。进一步地，人们通过外加磁场，发现这一低温反铁磁序可以被7-8 T 左右的面内磁场所抑制[139–141]；有限温度热力学及非弹性中子散射(INS) 测量到的非平庸的激发谱，也指出α-RuCl3中可能存在分数化激发，并称其为邻近自旋液体态(Proximate Spin Liquid State)[122,135,142]。除此之外，其他的探测手段，如核磁共振(NMR)[140,143,144]、拉曼散射[145]、电子自旋共振[146]、太赫兹谱学[147,148]，以及磁扭矩[149,150]实验等，也都从各个方面讨论了α-RuCl3中存在Kitaev 自旋液体态的可能性。在低温下人们还在α-RuCl3的一定磁场区间内，观察到了热霍尔效应的信号[151–156]，推断该材料在此低温磁场区间内，存在演生的马约拉纳分数化激发。

虽然α-RuCl3的相关实验研究积累了大量的实验数据和现象，但人们十分关心的若干科学问题仍未达成共识，例如α-RuCl3的有效自旋哈密顿量是什么？外加磁场抑制低温反铁磁序后，系统进入何种磁无序相？是否可以通过磁场调控手段在α-RuCl3中寻找到奇特的量子自旋液体？带着这些问题，作者采用张量网络态方法对α-RuCl3材料开展了多体计算研究。

D. α-RuCl3 微观自旋模型

针对α-RuCl3，此前人们提出了多个候选模型[121,123,127,142,157–164]，这些自旋模型主要是从密度泛函计算中得出(部分是从分析包括中子散射等谱学实验数据得到)，其中不同相互作用项的大小，甚至符号都暂无定论。目前，人们尚未能实现通过同一套模型参数定量复现出主要的热力学和谱学实验结果[165]，这严重阻碍了人们对α-RuCl3中量子自旋物态的深入理解和精确调控。

下面作者运用有限温度XTRG 方法[28,30]分析α-RuCl3的热力学测量数据，并结合其他多种多体手段，综合分析并研究其中的磁性物态。考虑六角晶格上的Kitaev-Heisenberg-Γ-Γ′(K-J-Γ-Γ′) 模型，其哈密顿量为

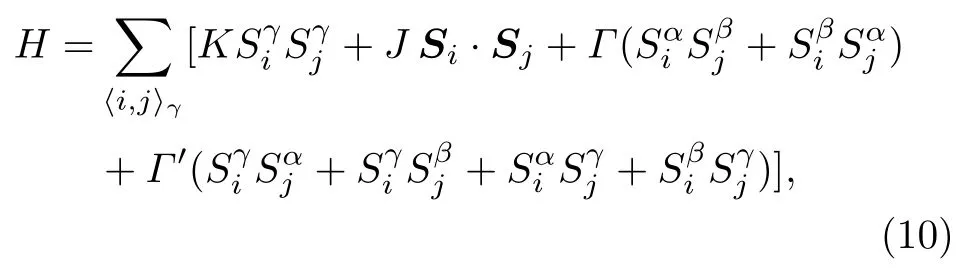
其中K表示Kitaev 相互作用，J表示海森堡相互作用，Γ和Γ′标记非对角项。该模型的空间群为D3d×ZT2，其中群符号={E,T}表示模型具有时间反演对称性。由于自旋–轨道耦合效应，D3d中的每一个元素都对应晶格转动与自旋旋转的一种组合，因此对模型的一部分物理性质提出了限制，例如朗德因子g和磁化率应该是单轴的。

此外，为了讨论磁场的影响，作者在哈密顿量中引入磁场项，并主要关注在以下两个方向：(1) 平行于六角晶格平面的方向；(2) 垂直于六角晶格平面的H[111]‖ c*方向。上述两方向相应的朗德因子分别为gab(=g[11¯2]) 和gc*(=g[111])，其中[l,m,n]表示自旋空间中的磁场对应的三个分量方向。因此，磁场与局域磁矩间的塞曼耦合就可以写为其中S[l,m,n]≡S · dl,m,n。在上式中，S= (Sx,Sy,Sz)，dl,m,n=

作者采用有限温度XTRG 算法[28,30]计算热力学性质，发现计算得到的磁比热cm曲线、两个方向的磁化率χab和χc*曲线，都对Γ项很敏感；且有无Γ′(J)项，会很大程度上改变cm和χab的低温性质。因此，通过拟合实验上的磁比热以及面内、垂直面方向的磁化率数据[122,132–137](相关拟合结果见图17(a, b) 所示)，作者确定了一组参数，即K=-25 meV，Γ= 0.3|K|，Γ′=-0.02|K|，J= -0.1|K|，朗德因子gab= 2.5，gc=2.3，可以很好的拟合实验结果，并成功地解释实验上观察到的现象。

在作者所定出的模型中，铁磁Kitaev 相互作用占主导地位，反铁磁的Γ项次之，其符号与此前的实验工作[125,127,157]和第一性原理计算[105,123,159,160,165]的研究结果是定性一致的。按照上文的讨论，当Kitaev 相互作用项占主导作用时，系统会在中间温度进入分数液体相(见上节IV.B)[130]，这可以自然地解释实验上观察到的邻近自旋液体行为特征[122,135,142]。在图17(c) 中，作者利用从上述热力学数据确定的K-J-Γ-Γ′模型开展DMRG 计算，所得零温磁化曲线与低温实验测量结果也十分相符。

作者还通过对照动力学测量数据来证实微观模型的有效性和精确性。图17(d) 中应用精确对角化方法计算了两个动量点Γ 和M 点处的散射强度，可以看到模型计算结果与实验测量结果在定量上是一致的。散射强度的峰值位置[135]，即ωΓ= 2.69±0.11 meV 和ωM= 2.2±0.2 meV，以及实验上看到的Γ 点亮度及双峰结构[141]，都可以被模型成功地描述。此外，非弹性中子散射的实验在低能及中间能量区间，测出了具有标志性的“星形”动力学结构因子[122,135]，而基于上述K-J-Γ-Γ′模型的动力学计算也可以给出这一重要特征。

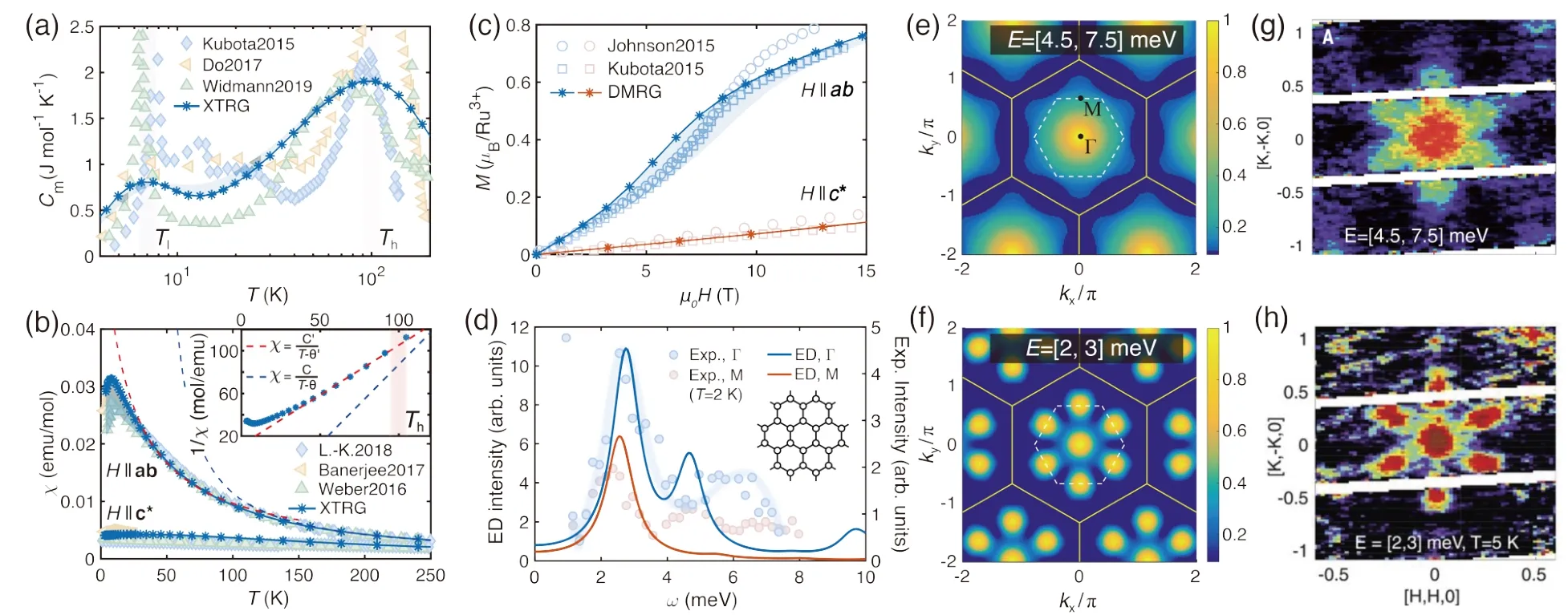
图17.基于所提出的K-J-Γ-Γ′ 模型，作者在尺寸为YC 4×L×2 的系统中计算了(a) 磁比热cm 曲线[122,132,133]，(b) 面内及面外方向(1 T 左右) 的磁化率χab 和χc*，并与实验结果[134-136] 进行对比。图中的阴影区域表示长度L 分别为4 和6 时的有限尺寸差异。(c) DMRG 计算得到的面内及面外方向的磁化曲线M(H)，并与实验结果[132,137] 进行对比。(d) 精确对角化方法计算的Γ 点和M 点的动力学结构因子，并与中子散射实验数据I(k,ω) 进行了对比，此处系统尺寸固定为具有C3 对称性的24 格点系统(见插图)。在(e) 和(f) 中，作者将上述强度分别在[4.5, 7.5]meV 和[2, 3]meV 区间进行积分，得到相应的结构因子，与(g) 和(h) 中的实验测量结果一致[135]。(引自文献[46] 图2，文献[135] 图2 及图3)

具体地说，在图17(e,f)中，作者将原子形状因子考虑到模型计算中来，对相应能量区间的散射强度I(k,ω)进行积分，讨论它们在不同动量点处的结构因子。实验结果如图17(h)所示，当系统处于低能量区间时[135]，动力学结构因子在Γ 点和M 点都有显著亮度，图案呈现花瓣形状；而当系统处在中间能区时[122,135]，动力学结构因子会变得连续，呈现出六角星形结构(图17(g))。由于此时星形结构的六个尖角位于M 点附近，这一特征也被称为M 型星形结构[165]。在图17(e, f) 中，作者对所确定的K-J-Γ-Γ′模型开展动力学性质计算，可以得到这两种形状特征的动力学结构因子。

E.场致量子相变与有限温度–磁场相图

Kitaev 自旋液体候选材料α-RuCl3在面内磁场下的相图一直是众多实验和理论工作探讨的重要问题。热霍尔效应[151–156]、拉曼散射[145]、热膨胀[166]测量等实验支持在“之字形”反铁磁和高场极化相中间存在一自旋液体相；而磁化曲线测量[132,137]、非弹性中子散射[141]、核磁共振[140,143,144]、电子自旋共振[146]、磁格林埃森参数[167]和磁扭矩[150]测量等实验认为，当面内方向的磁场抑制住α-RuCl3材料中的低温反铁磁序后，从反铁磁到高场极化相间只有一次相变(此外，由于面间堆叠效应[168]，在极化相前可能还会出现另一种“之字形”反铁磁序)。因此，在本小节中作者利用前文确定的微观自旋模型来研究α-RuCl3的磁场诱导效应，讨论其是否存在中间相，并给出其基态及有限温度相图。

从图18(a, c) 所示的比热容cm/T和等熵线的轮廓图中，作者识别出零场下的转变温度约为7 K，低温下的转变磁场约为7-8 T，与实验结果一致。同时，在图18(a,c) 中也可以看到，当系统处于反铁磁相时，低温温度尺度Tl会随着磁场增大而降低：在磁场不大时降低得较慢，临近相变磁场处降低的较为迅速。当磁场方向从a轴偏转55°时(即沿着H[110]对应的c′方向)，作者的模型也可以给出此时抑制“之字形”磁有序的临界场hc[110]=μ0H[110]≃10 T，这些计算结果均与实验测量结果高度一致[132,140,143](图18(b, d))。

综上，基于所定出的α-RuCl3有效K-J-Γ-Γ′模型，应用XTRG、DMRG、VMC、ED 等多种多体计算方法，作者计算了面内磁场下的基态及有限温度性质，确定α-RuCl3的有限磁场相图。作者把结果总结在图19(a, c)中，即当面内磁场H[11¯2]增加时，从反铁磁到极化相之间，模型计算支持只存在一次量子相变且不存在中间自旋液体相。

另一方面，基于模型计算得到的有限温度相图(图19(a)) 可以对解释实验上不同观察之间的分歧提供帮助。实验上，人们在温度为4-6 K 时的中间磁场区域中，探测到了很强的热霍尔效应信号[151,169]，但当磁场继续变化或者温度继续降低到2 K 左右时，观察不到量方向磁场下的比热容轮廓图，同时白色虚线描画出了低温温度尺度Tl和Tl′。零温轴上的红色圆点表示在临界磁场7 T 及10 T 时，系统发生了一次量子相变。在(c) 和(d) 中，作者展示了两个磁场方向相对应的等熵线，发现在中间温度分数液体相中，热力学熵的大小约为(ln 2)/2。(引自文献[46]图4)子化霍尔信号[151,169]。结合模型计算得到的结果，作者认为这可能是由于在面内场驱动的相变点附近(中间磁场区间)，虽然基态不是自旋液体相，但是分数液体可以生存到相对较低的温度。所观测到的热霍尔电导有可能来源于中间温区分数液体相中的马约拉纳分数激发。

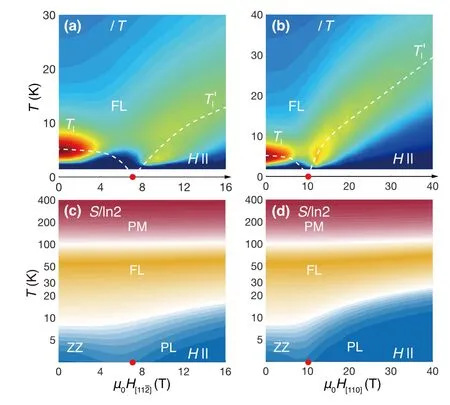
图18.磁比热cm/T 及等熵线的轮廓图，其中ZZ 表示“之字形”反铁磁相，PM 表示顺磁相，FL 表示分数液体相，PL 表示极化相，相应的相变点用红色圆点标记在横轴上。在(a) 和(b) 中，作者分别展示了加面内方向 ‖ a 及面外H[110] ‖ c′

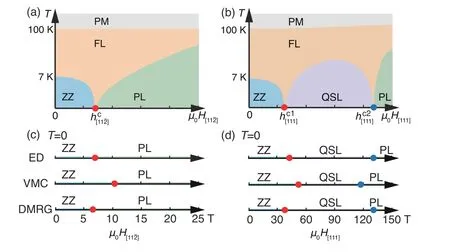
图19.(a) 和(b) 面内磁场和垂直平面磁场中的有限温度相图。相应的相变点分别用红色和蓝色的圆点标记在横轴上。(c) 和(d) 精确对角化(ED)、变分蒙特卡洛(VMC) 及DMRG 计算得到的基态相图，其中相变点的位置与有限温度结果一致。(引自文献[46] 图1)

正如作者在之前的章节中讨论到的，理想的Kitaev模型存在热分数化现象，巡游的马约拉纳费米子和Z2规范通量自由度在不同温度尺度上各释放一半的热力学熵[117]，从而在中间温区展现出Kitaev 分数液体相。这样新奇的分数液体相在扩展Kitaev 模型中是存在的[130]，在作者所提出的实际描述α-RuCl3的模型中也仍旧稳定存在(图19)，这很好地支持了此前的实验结论[122]。

除此之外，作者也计算了面内磁场为μ0H[11¯2]=4.2 T 时分数液体区的静态结构因子。在图20(d-f) 中可以观察到，除了Γ 点和M 点的亮斑，结构因子还展现出条纹状背景，与理想Kitaev 模型中所观察到的十分类似[130](图20(a-c))，反映出分数液体相中有键方向依赖的极短程自旋-自旋关联。这样的条纹状背景会随着自旋分量γ的变换而在动量空间相应转动，这是因为自旋关联当且仅当位于最近邻γ类型的键上时，才有非零值。基于上述理想(图20(a-c))和实际模型(图20(d-f))计算，作者指出可以通过对α-RuCl3进行极化中子漫散射实验观察如图20 所示具有显著条纹特征的自旋结构因子Sγγ(k)，从而验证在该材料中Kitaev相互作用以及中间温度分数液体的存在。

F.强磁场自旋液体态

接下来，作者改变磁场方向，研究系统在施加面外磁场H[111]‖ c*(即垂直六角晶格平面) 下的相变情况。根据基态及有限温度计算结果，作者发现，当施加H[111]方向的磁场时，在低场“之字形”反铁磁相和高场极化相之间，会存在一由面外场诱导的自旋液体相。随后，作者与强磁场实验工作者合作，在高场磁化率实验中确实探测到了这一中间相存在的实验证据。

作者首先计算了比热容cm和Z2规范通量的有限温度结果，其轮廓图如图21(a, b) 所示。在图21(a) 中，作者发现当面外磁场处于35 至130 T 的中间相时，有限温度下的比热容呈现出双峰结构，且峰值对应的温度代表两个温度尺度，分别对应短程自旋关联和规范通量的建立。在图21(b) 中，作者计算了Z2规范通量Wp，发现其在低温下，磁场为处，会从负值转变为正值；在磁场为处，其值几乎为零，并最终在极化场中趋于一个很小的正值。上述通量在不同区域之间的符号变化，与近期DMRG 及张量网络在K-Γ-Γ′模型上的研究结果[171,172]十分一致，表明磁场和为两相变场。值得注意的是，与理想Kitaev 模型中的通量相比，此时的通量Wp不再是严格守恒量，因此其低温期望值|Wp|一般不等于1[130,171,173]。

此外，计算表明当面外磁场处于中间相时，系统在Th附近会释放约为(ln 2)/2 的热力学熵，在附近释放另一半(热分数化)；当温度低于Th时，自旋关联会被建立起来，磁化率曲线会展现出与Kitaev 模型的情况相似的演生的居里行为；随着温度继续降低，系统中的通量逐渐被“冻结”。因此，从上述热力学结果中，作者发现面外磁场与面内磁场情况截然不同，其中间磁场处会演生出另一个具有双温度标度、与原始Kitaev模型一样升温存在热分数化的自旋液体相。根据上述结果，作者给出如图19(b) 所示的有限温度相图。

为了精确的定出零温下的两个相变点，在图21(c)中，作者应用DMRG 算法计算了c*方向的磁化曲线M(H[111]) 及其导数dM/dH[111]。根据DMRG 计算结果，作者发现此时磁化曲线M(H[111]) 会有两次快速上升，对应磁化率dM/dH[111]展现出两个尖峰结构，表明在面外磁场下存在两次相变，这一结果也可以从图21(d) 中展示的精确对角化计算得到的能谱中得到印证。根据DMRG、ED、VMC 等的计算结果，作者得到了如图19(d) 所示的基态相图。值得提及的是，从上述计算结果中，作者发现低相变场35 T，与近期各向异性系数的实验[150]测得的结果高度一致；模拟所得到的高相变场hc2[111]在100 T 量级附近，可以通过脉冲强磁场实验来进行验证。

当面外磁场为45.5 T 时，作者在图21(b) 的插图中展示了中间温度及基态的自旋结构因子从中作者发现在中间温度及基态中结构因子都没有展现出磁有序峰，且在其布里渊区中，均可以观察到奇特的与键方向有依赖关系的自旋关联特征(条纹状背景)，这与“之字形”反铁磁相中的自旋关联有显著不同，支持中间自旋液体相的结论。

最近，东京大学脉冲强磁场实验室开展了100 特斯拉级低温(4 K) 强场磁化率测量，发现α-RuCl3在35和90 T 两处存在量子相变，提供了中间相存在的实验证据[174]。为了研究这一中间量子自旋液体会如何随着磁场方向的改变而变化，作者将实验测量和理论计算的结果进行了对照得到了有限磁场–有限角度相图，发现这一可能的量子自旋液体态会在相图中延伸出一定区域，而其关联和拓扑性质的更全面刻画有待后续实验和理论工作的进一步研究。

综上所述，通过精确确定模型并开展多体计算与分析，作者预言在低温温度尺度以下、面外磁场范围和之间，α-RuCl3材料会进入到中间磁场量子自旋液体相，并通过与强磁场实验组合作找到了中间自旋液体相存在的证据。

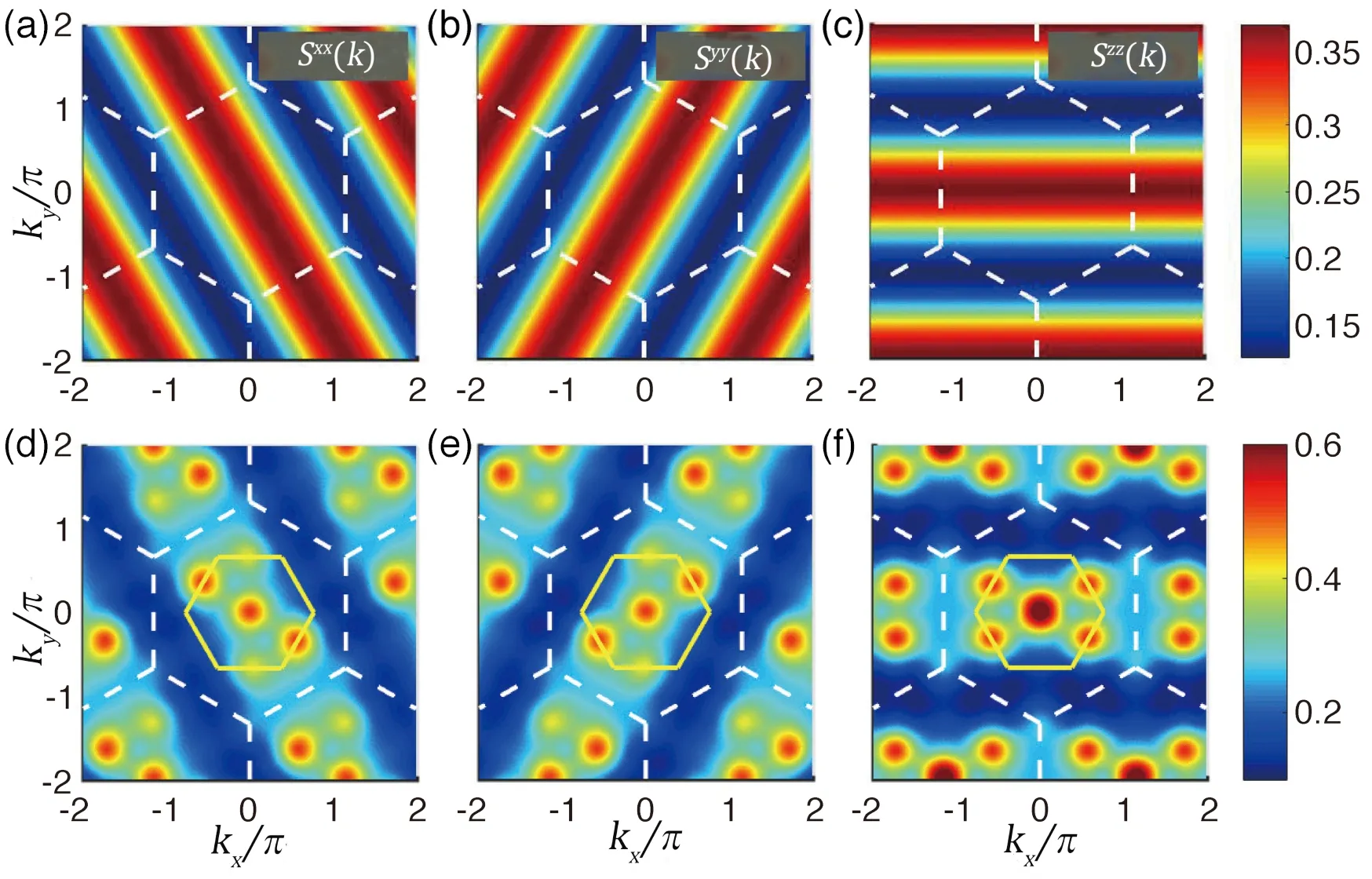
图20.(a～c) Kitaev 模型在中间温度T = 0.15 时的静态结构因子Sγγ(k) 轮廓图，其中γ = x、y、z 分别表示自旋三个分量的方向。(d～f) α-RuCl3 有效模型在10.6 K，4.2 T 时对应的静态结构因子，同样能观察到与键类型有关的条纹状背景，其中M 点峰值源于此时的系统具有“之字形”反铁磁关联。(改编自文献[130] 图9 及文献[46] 图3)

V.总结与展望

关联与拓扑是当今凝聚态物理的两大研究主题，且二者在阻挫量子磁性研究中不断交汇与融合，使其成为一个活跃的研究领域。低维量子磁体提供了理想的材料平台，使得多体理论与实验研究在这一领域紧密地结合起来，共同探讨超越LGW 范式的新奇量子物态与相变。其中，量子自旋液体作为一类新奇的磁性状态，吸引着凝聚态物理工作者广泛的研究兴趣。量子自旋液体体系在零温时不会形成长程的磁有序，但伴随着长程的拓扑纠缠及分数化的激发模式，在拓扑量子计算等领域中有潜在应用前景。实验上，人们提出了系列量子自旋液体候选材料，积累了大量宝贵的阻挫磁性材料的热力学测量结果，但因为计算的挑战性(如量子蒙特卡洛方法会遭遇“负符号问题”而难以降至低温)，鲜有数值模拟结果直接对这些热力学数据开展分析，“挖掘”阻挫磁性材料背后的微观自旋模型。本文介绍了有限温度下的张量重正化群方法，包括线性(LTRG)和指数张量重正化群(XTRG) 等，这些方法在计算相应系统有限温度性质、拟合相应阻挫磁体的热力学测量结果、精确确定微观模型等过程中发挥了重要的作用，搭建起了理论与实验之间的“桥梁”。

在本文中，作者首先研究了正方晶格上的海森堡模型以及横场伊辛模型等，精确得到自发磁矩以及相变温度等结果，证实了XTRG 方法具有很高精度；同时，在对三角晶格海森堡模型的热力学性质研究中，揭示出其奇特的双温度标度及中间温区的类旋子激发图景。在这之后，作者对三角晶格阻挫磁体TmMgGaO4展开研究，确定其微观模型参数，预言具有演生的U(1) 对称性并存在两次Berezinskii-Kosterlitz-Thouless (BKT) 拓扑相变，并结合实验验证，为在磁性材料中研究这类新奇拓扑相变提供实际的材料平台。

随后，作者应用XTRG 方法，计算了扩展六角晶格Kitaev 模型的有限温度性质，发现对于有限磁场下的Kitaev 模型等，在一定的参数区间内，系统在中间温区均会展现出分数液体特征，其中磁化率涌现出普适居里行为，自旋静态结构因子具有条纹状背景，这些特征可以与金属型比热容、热力学熵的平台一起，作为实验上研究Kitaev 顺磁物理的热力学依据。在这之后，作者把目光投向重要的Kitaev 自旋液体候选材料α-RuCl3，通过拟合其比热容和磁化率测量结果，确定了其微观哈密顿量为K-J-Γ-Γ′模型，并计算得到了α-RuCl3有效模型在不同方向磁场中的有限温度相图，预言其在垂直面场下会存在由场诱导的中间磁场自旋液体相。随后，脉冲强磁场磁化率实验探测到了此中间相存在的证据，这一理论密切结合实验的研究路线为后续更多Kitaev 材料的场致自旋液体研究提供了重要基础。

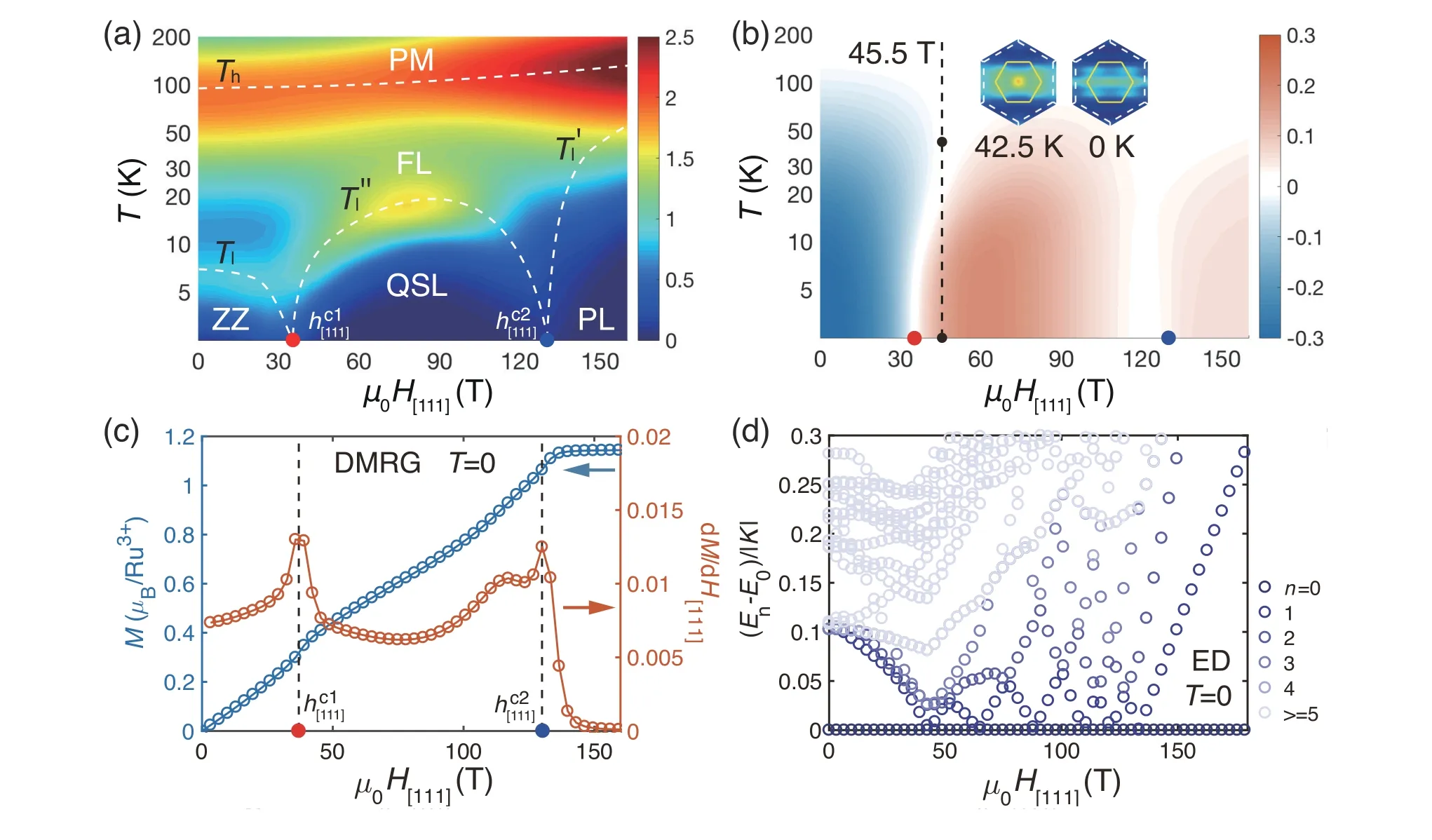
图21.面外方向磁场H[111] ‖ c* 下的高场自旋液体相。(a) 比热容cm 的轮廓图，可以看到在低场及中间磁场区间内，比热容都会呈现双峰结构。为了叙述方便，作者用白色的虚线描画出了温度尺度Th, Tl、和T′′l 的位置，对应相图中的各个相边界。(b)为Z2 规范通量Wp 的轮廓图，橙色表示Wp 的值为正数；蓝色表示Wp 值为负。在插图中，作者展示了μ0H[111] = 45.5 T处的零温及有限温度下的自旋结构因子(k)。在(c) 中，作者用DMRG 计算了零温的磁化曲线及其导数dM/dH[111]，表明在高面外场下，系统中存在两个相变磁场 及(用红色及蓝色圆点表示)。(d) 精确对角化方法计算的能谱En-E0，在中间相中可以观察到大量低能本征态。(引自文献[46] 图5)

作为展望，作者指出在三角晶格和Kitaev 六角晶格等系统中还存在大量的新颖阻挫量子磁体有待研究，如NaYbO2[62,175,176]、NaYbS2[177]、NaYbSe2[178,179]和CsYbSe2[180]等可能受无序影响较小的Yb 基材料，是近年来三角晶格自旋液体实验研究的焦点。这类材料在低温下均没有展现出磁有序[175,178–180]，并伴有自旋动力学信号[175,177,181]，如NaYbO2的激发谱在布里渊区中的K 点展现出连续色散关系[62,175]，有望实现三角晶格量子自旋液体态。

在Kitaev 自旋液体候选材料方面，人们也提出了很多其它基于Jackeli-Khaliullin 机制的4d 或5d 电子类型的阻挫磁性材料，如铱氧化物家族的Cu2IrO3[182]、Ag3LiIr2O3[183]、Cu3LiIr2O3[184]、H3LiIr2O3[185]，和卤族化物RuI3[186]、RuBr3[187]、YbCl3[188]、CrI3[189]等。其中YbCl3在0.6 K 以下为长程的奈尔反铁磁序，会被6 T 左右的面内磁场抑制住[188]；CrI3为有效自旋3/2 的系统，但层间耦合效应比较显著[189]；其它材料目前只有粉末样品，还有待未来生长出大尺寸单晶样品并进行更为系统的实验测量。此外，最近的研究表明由Co2+、Ni3+等高自旋的d7电子，也可以在材料中实现Kitaev 相互作用[190]，如Na2Co2TeO6[191,192]、Na3Co2SbO6[193]、BaCo2(AsO4)2[194]等。目前，实验上认为Na2Co2TeO6和Na3Co2SbO6的基态可能也是“之字形”反铁磁序，且居里–外斯温度有很强的各向异性，与α-RuCl3的特征十分相像。同时，比热容、磁化曲线、电子自旋共振等实验发现Na2Co2TeO6材料在一定磁场间，存在类似量子自旋液体的无序相[191,192]；具有高质量的单晶样品的BaCo2(AsO4)2在低温(约为5.5 K) 以下也形成反铁磁序[194]。磁化曲线、比热容、热导实验表明这一反铁磁序会被0.5 T 左右的面内磁场所抑制，与α-RuCl3展现了类似的特征，且相变场更低。因此这类Co 基六角晶格材料的有效微观模型为何、在磁场的调控下具有何种新奇物态、是否是Kitaev 自旋液体材料等有趣问题都亟需进一步开展深入的研究。

综上所述，本文通过若干具体的例子，展示了有限温度张量重正化群方法在研究量子自旋微观模型、典型阻挫磁性材料体系并预言其新奇物态性质等方面发挥的重要作用。有限温度张量重正化群方法是理论与实验之间一架有力的桥梁，借助其可以开展阻挫量子磁性系统的多体计算研究。作者期待随着多体计算方法的进一步发展，这样的多体研究方案能够帮助人们更好地探索包括量子自旋液体在内的新奇量子物态及其在关联量子材料中的实现，不断拓展人们关于量子磁学以及其它关联物质科学的认识。

致 谢

本文感谢国家自然科学基金(11974036、11834014)的支持。本文作者感谢戚扬、孟子杨、温锦生、于伟强、刘正鑫、邬汉青、龚寿书、胜献雷、Yasuhiro H、Matsuda、周旭光等在相关研究上的密切合作，以及陈斌斌、高源、屈代维、李乔依等的有益讨论。