基于机器学习的样本均值近似算法求解应急物资配置问题

□ 胡少龙 范婷睿

（西南交通大学 1.经济管理学院，四川 成都 610031；2.服务科学与创新四川省重点实验室，四川 成都 610031）

一、引 言

洪水、地震、飓风等自然灾害易破坏基础设施，造成大量灾民无家可归，需快速向灾民提供应急物资。为了实现这一目标，需在灾前选择合适的区域储备充足的物资，以便灾后高效配送[1]。应急物资配置通常涉及设施选址和库存两个关键决策，其中设施选址决策包括物资储备库选址或临时配送中心选址等；库存决策指不同物资的储备量。学者多应用混合整数规划理论构建数学模型，优化应急物资配置决策。刘波和李砚[2]、王苏生等[3]构建了双层规划模型，优化灾后应急物资分配问题。葛春景等考虑多个受灾点同时且多次需求的情况，构建了一个多重覆盖选址的混合整数规划模型，优化物资配置决策[4]。于冬梅等从提高服务质量的视角，考虑设施中断风险，建立了选址布局网络的多目标混合整数规划模型，优化设施选择决策[5]。

自然灾害难以预测，受灾范围、发生时间等灾情信息具有不确定性。为保障应急物资配置效率，需要考虑上述不确定因素。作为研究不确定环境下的最优决策理论，随机规划是研究上述问题的有效工具。张庆和余淼[1]、 张梦玲等[6]、王海军等[7]、Wang 等[8]构建随机规划模型，优化灾前物资配置和灾后物资配送等决策。Sanci 和 Daskin[9]、Moreno 等[10]还考虑了道路受损的情况，构建随机规划模型，优化应急物资配置和网络恢复的联合决策。Wang 等基于手机定位数据获取灾害信息构建情景，以优化选址和配送等决策[11]。

面对大规模问题，优化软件和精确算法往往难以在可接受时间内求得最优解，启发式算法具有广泛的应用场景。近年来，越来越多的学者将机器学习与优化算法结合，以提高求解效率。李壮年等应用NSGA- Ⅱ遗传算法求解多目标优化问题，分别提出了基于特征工程和支持向量机等六种机器学习算法的参数优化方法[12]。Fu 等应用统计机器学习理论降低随机变量的维数和情景尺度[13]；Guevara 等提出了一种机器学习和分布鲁棒优化相结合的方法[14]；Ghasemi 等建立了基于机器学习的仿真元模型[15]；Zhang 等提出了一个基于极限学习机的集成学习模型和多目标规划的优化框架[16]。

样本均值近似算法（Sample Average Approximation，SAA）是一种求解大规模随机规划问题的近似算法。Murali 等将禁忌搜索算法与SAA 结合[17]，Aydin 和Murat 提出了一种基于群体智能的SAA[18]，Li 和Zhang等在SAA 中引入了情景分解算法[19]，Bidhandi 和 Patrick 提出了一种基于加速采样的方法改进SAA[20]，Jalali等提出了一种基于SAA 的遗传算法[21]，Jiang 等提出了一种将SAA 与牛顿迭代相结合的方法[22]，Tao 等将SAA 与基于种群进化的人工藻类算法相结合[23]，以提高求解大规划随机规划模型的效率。但是，以上研究难以保障生成最具代表性的样本，以保证计算效率。如图1(a) 所示，当一个样本包含情景A 和C，另一个相比包含情景B 和C，则后者的代表性显然较弱。这是由于情景B 和C 距离较近，所含有的信息比较相似。为解决该挑战，Emelogu 等提出了一种基于机器学习的SAA，其中机器学习用于生成样本[24]。作者利用聚类技术（如k-means）将相似情景进行聚类，然后随机从每一簇选择一个情景作为该簇的代表性情景，见图1（b）和（c）。该算法的局限性在于，当每一簇包含的情景数量不同时，只选择一个情景难以具有足够的代表性。因此，本文的贡献是提出整合分层随机抽样解决该挑战。通过标准差决定每个簇的情景选取数量，可以改善样本生成的合理性，以提高SAA 计算效率。

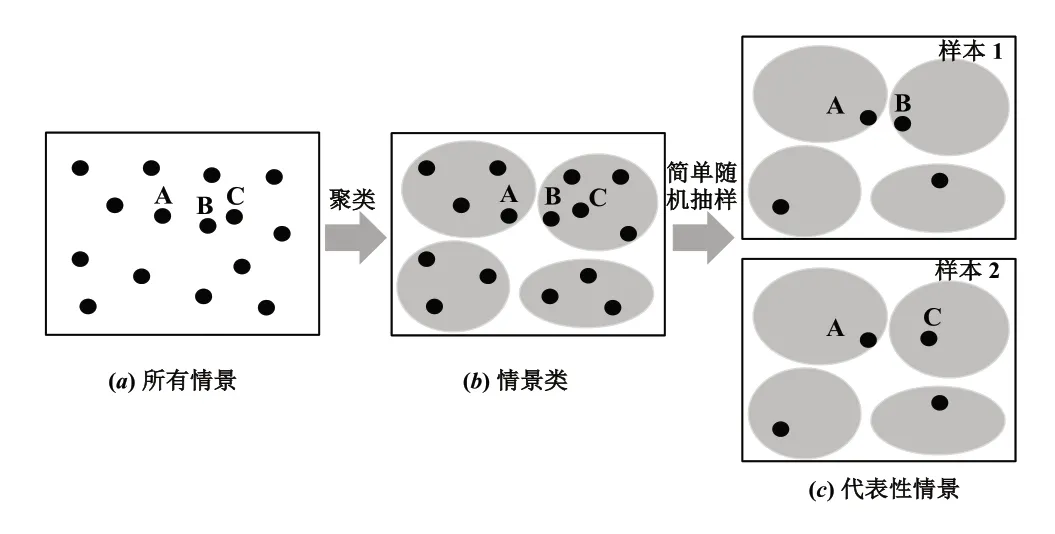
图1 基于聚类的样本生成过程

综上所述，综合考虑多种应急物资、不同的仓储设施类别和需求的不确定性，以设施的选址、库存和运输成本，以及物资供应不足的惩罚成本最小为目标，设计决策变量分别表示仓储设施选址、库存和灾后配送等决策，构建了基于情景的两阶段随机规划模型，优化应急物资配置决策。此外，应用SAA 求解模型，并整合了一个机器学习框架以高效地生成样本，进而提高SAA 的性能。所提出的机器学习框架使用k-means++ 对全部情景进行聚类，再应用分层随机抽样生成样本。

其余部分内容如下。第二节，构建应急物资配置随机规划模型；第三节，设计基于机器学习的SAA 算法；第四节，设计数值实验验证算法的有效性；最后，对研究进行总结，并讨论下一步研究方向。

二、应急物资配置随机规划模型

（一）问题描述

随机规划是一种处理优化模型输入值不确定性的技术之一，模型使用一组离散的情景表示不确定突发事件的影响范围和影响程度。例如，一种情景表示雅安发生7级地震，影响了周围市县120 万人；一种情景表示11 级台风在宁波登陆，影响了周围市县50 万人等等。两阶段随机规划是在不确定情况下，做出非预期的第一阶段决策；第二阶段决策是在第一阶段决策和情景已知情况下进行[25]，即如何决定应急物资配置，使得应对各种灾害情景的成本最小。具体地，构建情景集合描述不确定需求，以设施选址、采购、库存、运输和物资供应不足的惩罚成本最小的目标，优化应急物资配置。应急物资配置决策包括：仓储设施的选址和大小，每个设施中储存的各种物资数量，以及应对不同情景时物资的配送、剩余和短缺数量。

（二）模型构建

1.模型假设

考虑饮用水、食物、医疗包三种应急物资；不同设施的储备能力不同；不同物资的单位采购、运输、持有和惩罚成本不同，且不随情景变化。

2.符号说明

I 表示城市集合，由i,j索引。L表示设施类型集合，l∈L分别为大、中、小三种设施类型。A表示物资类别集合，a∈A分别为饮用水、食物、医药用品。S表示自然灾害情景集合，s∈S。随情景变化的参数包括情景发生概率sP和城市j对a类物资的需求Da,j,s，令未受灾城市的需求量为0。储备设施相关参数包括l类设施的容量Ul，l类设施的固定成本ClF。Hi,j表示城市i到j的距离，aV表示a类物资的单位体积，C aP表示a类物资的单位采购成本，C aT表示a类物资的单位运输成本，CHa表示a类物资的单位持有成本，aG表示a类物资的单位惩罚成本。当情景s发生后，所储备物资被迅速运往各受灾城市，若库存无法满足受灾城市的物资需求，则被视为物资供应不足。对此，设置惩罚成本aG，对未满足物资进行惩罚。

第一阶段决策变量包括：是否在i城市建造l型仓储设施xi,l，取值分别为0 和1；i城市a类物资储备量ya,i。第二阶段决策变量包括：情景s下，i城市运送到j城市的a类物资的数量qa,i,j,s；情景s下，j城市的a类物资的短缺数量wa,j,s；情景s下，灾害结束后i城市a类物资的剩余量za,i,s。

3.目标与约束函数

第一阶段使设施固定成本和物资采购成本最小，即fc、pc最小。第二阶段为当需求不确定时，运输、仓储和惩罚成本的期望最小。其中tc表示运输成本，hc表示剩余物资的库存成本，wc表示供应不足的惩罚成本。式（7）限制每个设施的采购总量不超过该设施的储存能力，式（8）限制每个城市最多只能建设一种类别的仓储设施，式（9）计算设施内应急物资的剩余数量，式（10）表示物资短缺量等于需求量减去已分配量。式（11）限定x只能取0或者1，式（12）为非负约束。

三、基于机器学习的样本均值近似算法

样本均值近似（SAA）是一种基于蒙特卡罗模拟的随机离散优化问题的求解方法。这种方法的基本思想是生成一个随机样本，然后用相应的样本平均函数来近似期望值函数。对得到的样本均值近似问题进行求解，该过程重复多次，直到估计目标值与下界的差值低于某一阈值时，停止迭代获取满意解[26]。SAA 中，更大的样本意味着估计目标值更接近真实值。但是，随着样本的增大，求解的复杂度也随之增长。因而，选择合适的样本量是SAA 的关键步骤。本节提出一种机器学习框架选取情景，以生成代表性样本，提高SAA 求解效率。首先，应用k-means++ 聚类方法对灾害情景进行聚类；然后，通过分层随机抽样方法获得样本。下面分别描述k-means++ 算法、分层随机抽样方法，以及改进后的SAA算法流程。

(一）k-means++算法

k-means算法也被称为Lloyd 算法，由Stuart Lloyd 在1957 年提出。k-means方法是最流行的无监督学习算法之一，它遵循一种简单和相对有效的方法，将给定的数据集分类成一定数量的簇。首先，令K为中心集合，随机选择初始的个中心。然后，数据集中的每个点被分配到最接近它的中心的簇中。最后，计算每个簇的均值作为中心值，并根据新的中心值重复第二步，直到中心值不变则算法收敛。与k-means的随机选择初始中心相比，k-means++ 通过不同数据点之间的距离，迭代的选择|K|个中心，以确保更快的收敛[27]。

k-means++算法步骤如下。

第一步：从需求数据集Da,j,s中随机选取一个需求点作为聚类中心Ca,j,1。

第二步：通过轮盘赌方法确定下个中心点，分别计算需求点和已选中心的距离，并计算概率。

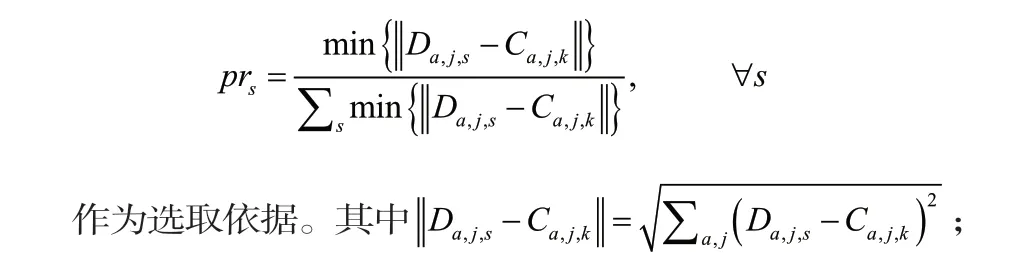
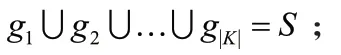
第五步：对每个簇gk，重新计算聚类中心

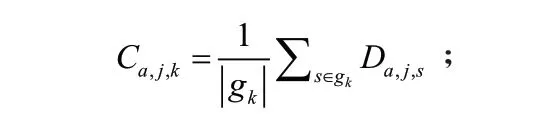
第六步：重复第4 和5 步，直到聚类中心位置不再变化。

(二）分层随机抽样算法

由于样本是聚类后从各簇中抽取得到的，抽取方式对于样本的选取也很重要。Emelogu 等应用简单随机抽样，从每簇随机抽取一个情景[24]，忽略了不同簇中情景数量差异较大时，选取一个情景难以具有代表性的问题。因此，提出了分层随机抽样算法应对该问题。首先，根据标准差计算各簇应抽取的情景数量。然后，通过随机抽样抽取情景。为防止随机抽取的情景所对应的需求量过大或过小，通过限定其平均值，以确保样本的合理性。例如，若抽取情景所对应的需求量都较大，模型偏好选取大型设施并储备过多物资，会造成成本过大。

分层随机抽样算法步骤如下。

第一步：根据标准差计算各簇应抽取的情景数量[28]。

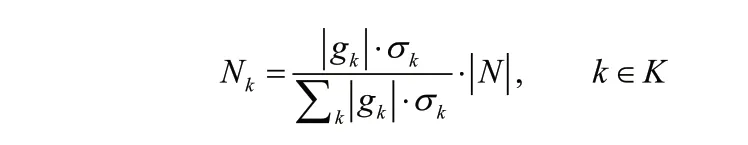
其中，σk为簇gk的标准差，表示样本的大小，表示每个簇抽取的样本数量；

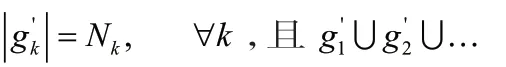
第三步：若

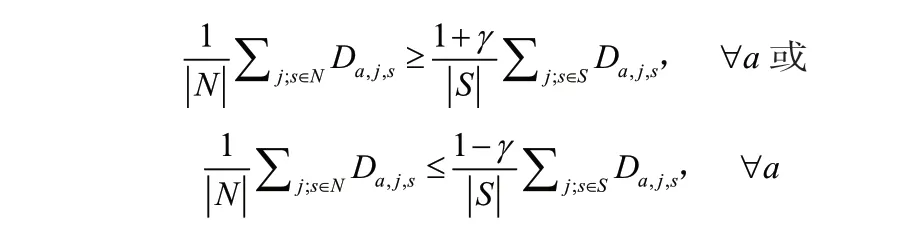
重复第二步，其中γ∈{ 0,1}；

(三）算法对比

为对比分析Emelogu 等提出的算法[24]与本文提出的算法在求解大规模随机规划问题的效率，本节分别描述了两个算法，应用胡少龙等[29]提出的SAA 框架。

本文提出的算法SKS：SAA，k-means++，以及分层随机抽样，如下。

第一步：应用k-means++算法；

第二步：应用分层随机抽样算法；

第三步：对任意m∈M，求解模型

第四步：使用全部情景集合S，且对任意m∈M，求解模型

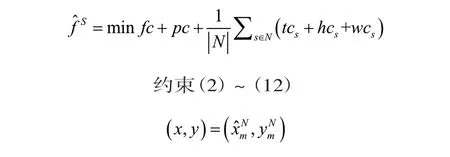
Emelogu 等[24]提出的算法SKR: SAA，k-means++，以及简单随机抽样，如下。

第一步：应用k-means++算法；

第二步：应用简单随机抽样，每簇抽取一个情景；

第三步：同SKS 算法的第三步至第六步。

四、算例分析

（一）算例构造

构造飓风灾害算例验证算法的有效性。假设有一飓风多发区域，各城市受灾情景受飓风登陆点和飓风等级影响，以下数据均来自已发表文献。飓风通常用萨菲尔——辛普森级来划分，Catg= {1 ,2,3,4,5}，其中5 级最严重。需求和概率两个参数随情景变化，其中，需求用受灾人数衡量，其取决于受灾城市的总人口、登陆城市和飓风等级。飓风的影响程度采用了Dalal 和Üster 提出的方法表示[30]：

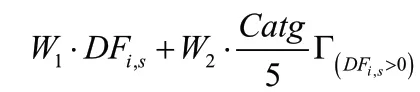
基于Rawls 和Turnquist 的研究[31]设立如下数据。考虑三种应急物资：水、食品和医疗包。假设水的单位是1000 加仑；食物为速食产品，以1000 餐为单位；医疗包为每人一个单位。表1 总结了应急物资的关键参数。假设每一种物资未满足的惩罚成本为采购价格的10 倍，持有成本为购买价格的20%。大、中、小三种不同存储容量的设施的固定成本和储存容量，见表2。

表1 物资的单位采购价格、所占仓储量和运输成本

表2 不同类别设施的固定成本和储存容量

（二）结果分析

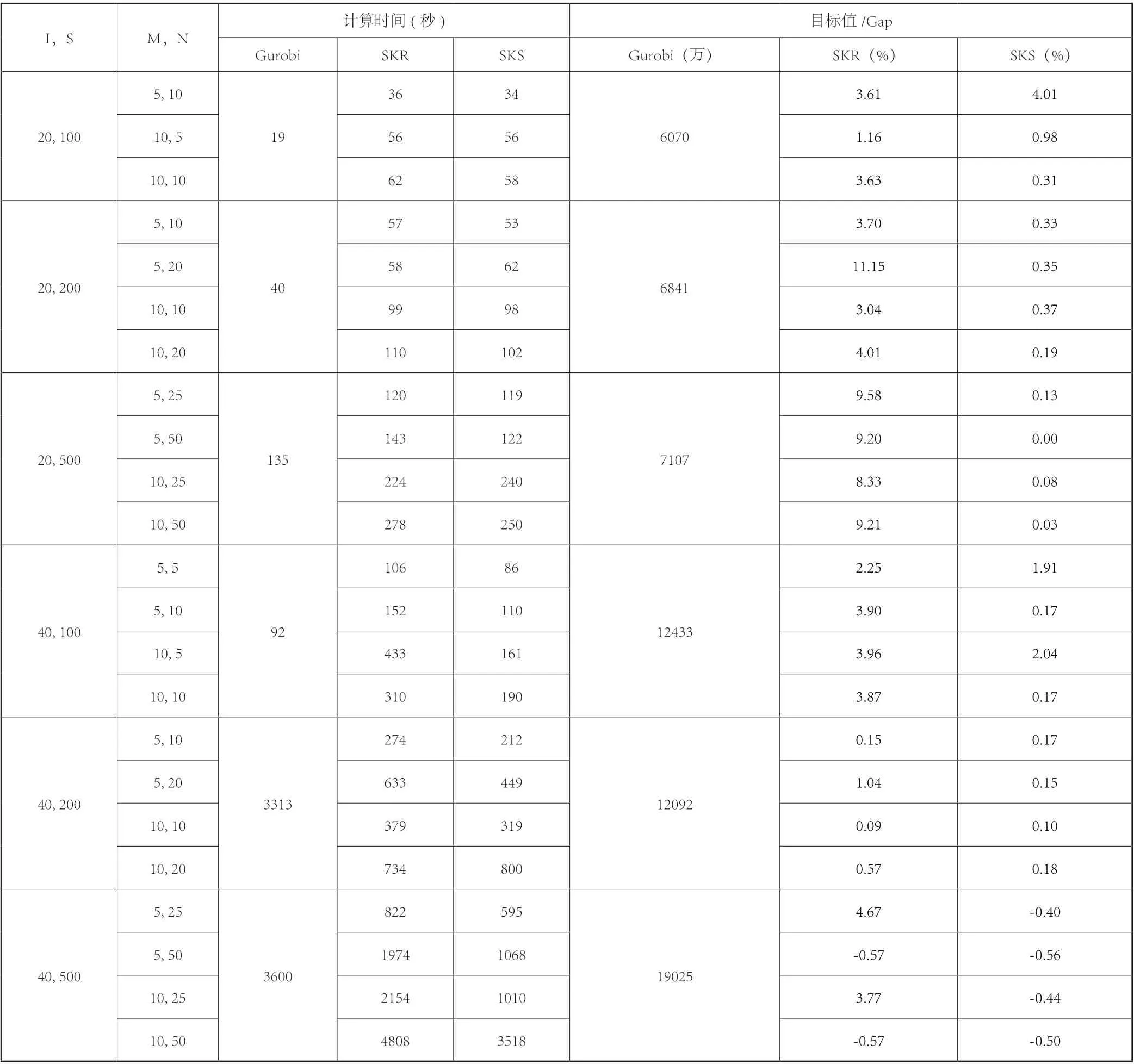
表3 三种算法的计算时间和估计目标值

I，S M，N计算时间(秒) 目标值/Gap Gurobi SKR SKS Gurobi（万） SKR（%） SKS（%）3.61 4.01 10, 5 56 56 1.16 0.98 10, 10 62 58 3.63 0.31 5, 10 36 34 20, 100 19 6070 3.70 0.33 5, 20 58 62 11.15 0.35 10, 10 99 98 3.04 0.37 10, 20 110 102 4.01 0.19 5, 10 57 53 20, 200 40 6841 9.58 0.13 5, 50 143 122 9.20 0.00 5, 25 120 119 20, 500 135 7107 10, 25 224 240 8.33 0.08 10, 50 278 250 9.21 0.03 2.25 1.91 5, 10 152 110 3.90 0.17 10, 5 433 161 3.96 2.04 10, 10 310 190 3.87 0.17 5, 5 106 86 40, 100 92 12433 0.15 0.17 5, 20 633 449 1.04 0.15 10, 10 379 319 0.09 0.10 10, 20 734 800 0.57 0.18 5, 10 274 212 40, 200 3313 12092 4.67 -0.40 5, 50 1974 1068 -0.57 -0.56 5, 25 822 595 40, 500 3600 19025 10, 25 2154 1010 3.77 -0.44 10, 50 4808 3518 -0.57 -0.50

为便于直观比较，计算不同算例SKR和SKS的平均求解时间，见图2。显然，对于小规模算例，Gurobi具有一定的计算优势。而当数据量增大时（城市数量为40，且情景数量超过100），Gurobi求解时间陡然增大。SKR和SKS的计算时间增幅较小，计算效率明显更高。此外，与SKR相比，当城市数量为20 时，SKS求解速度较快的优势并不明显。但是，当城市数量增大到40 时，SKS的计算时间一直较少，表明其计算效率更高。当M不变，N值增大意味着情景数量变多，算法的求解时间主要取决于样本问题的复杂性。例如，当I=40 、S=500、M=5 时，50 个情景的样本问题显然比25 个情景的更难求解。可通过整合更高效的算法求解样本问题，以提高SKR和SKS的计算效率。当N不变，M值增大意味着样本问题个数增多，求解时间则主要取决样本问题的计算时间。例如，当I=40 、S=500、N=25 时，10 个样本问题显然要比5 个求解时间更长。可通过整合并行计算，以提高两种算法的计算效率。

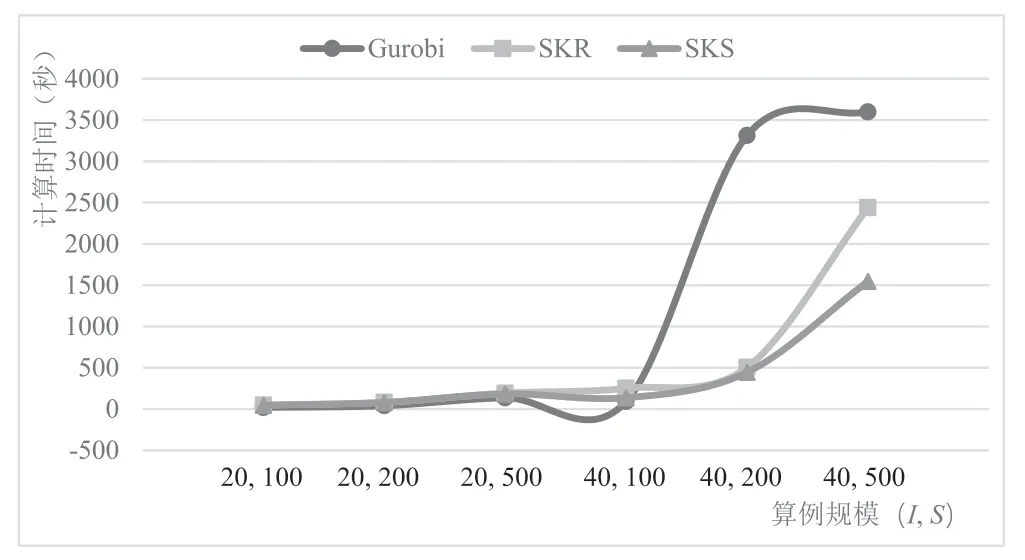
图2 Gurobi、SKR 和SKS 平均计算时间的对比

以Gurobi求解结果为基准，计算Gap值并比较SKR和SKS的计算效率。如表3 所示，对于算例I=40 、S=500，Gurobi在3600 秒内无法求得最优解，SKR和SKS可以在较短时间内找到更好的上界。因此，当问题规模增大到一定程度后，SKR和SKS在计算效率上都优于Gurobi。但与SKR不同的是，无论M和N值为多少，SKS都能找到更好的上界。对于不同算例，与Gurobi求解结果相比，SKR的Gap在-0.57%至11.15%之间变化；而SKS仅在-0.56%至4.01%之间变化。为更直观的对比不同算例下SKR和SKS的Gap值的变化，将不同算例下，两个算法的结果求平均值，其结果见图3。对于所有算例，显然SKS所求得的上界都显著优于SKR。因此，通过对比分析计算时间和Gap值发现，SKS明显优于SKR。

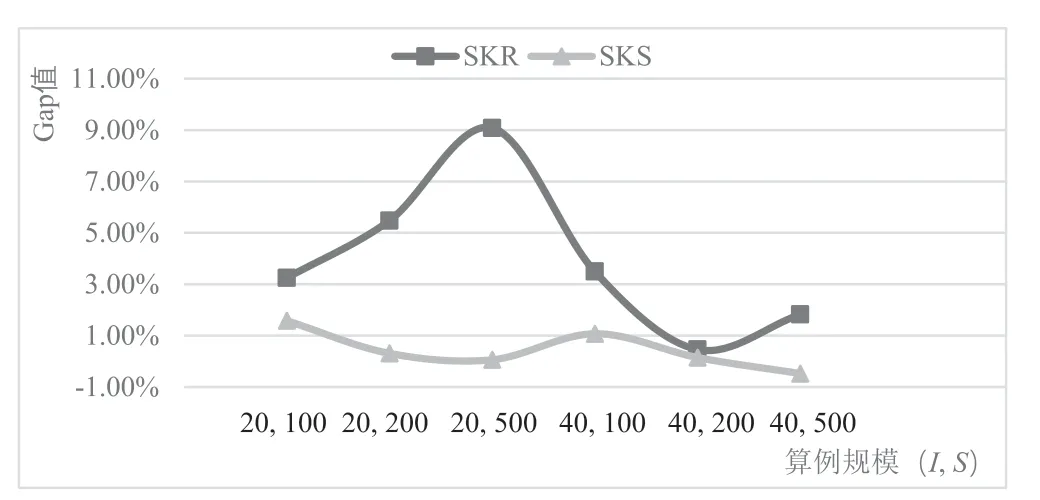
图3 SKR 和SKS 平均Gap 值的对比

五、结论

合理布局应急物资储备库并存储物资可以在灾害发生后及时做出响应，以缩短物资筹备及运输的时间。通过最大限度地提高应急物资供给能力，可以保障人民生命财产安全，降低突发事件所造成的损失。

考虑不确定需求，研究了应急物资配置的模型与算法，以优化应急物资储备库选址与库存决策。以设施选址、采购、库存、运输和供应不足的惩罚成本最小为目标，构建了应急物资配置的两阶段随机规划模型。同时，整合k-means++ 聚类算法和分层随机抽样，设计了一个机器学习框架生成样本，以改进样本均值近似方法，提高其在求解大规模随机规划问题的计算效率。最后，构建了灾害情景对模型和算法进行了仿真验证，通过与Gurobi和其他算法的对比分析表明，随着算例规模增大，所提出的算法能在较短时间找到更好的上界。

尽管为求解大规模随机规划问题提供一条新的途径，但研究仍存在不足，可从以下方面进一步完善。首先，仅考虑了单一的灾害后果，未考虑到交通受阻、设施受损等的影响，需在后续的研究中加以讨论。其次，如何有效确定簇的数量。k-means++算法容易理解，聚类效果好，尤其是在处理大数据集的时候，可以保证较好的伸缩性和高效率。但是，初始k 值需要人为设定，该数值选取常依靠经验，可能带来较大误差。仅根据样本数量设定k值，需要进一步改进。最后，未对比其他聚类算法的效果。下一步研究可以增加不同的聚类算法，通过实验对比分析各聚类方法与SAA 结合后的优劣。