不同加载方式对输电铁塔风致响应的影响

伍川， 张博， 刘泽辉， 杨晓辉， 李超， 赵洋*

(1.国网河南省电力公司电力科学研究院， 国网输电线路舞动防治技术重点实验室， 郑州 450052； 2.重庆邮电大学先进制造工程学院， 重庆 400065)

输电塔线体系承担着电能的传输、分配、调节等作用，其安全性和稳定性非常重要，因恶劣气候条件而引起的架空输电线路破坏会导致电力系统瘫痪，带来的后果不可估量[1]。风载荷作为最常见的外部载荷，在高压输电线路杆塔设计中需要特别关注。

输电塔线体系由于其复杂的耦合效应特性会使其风振响应的评估过程变得十分复杂[2]，学者们主要从静力分析和动力响应分别探讨其力学性能。厉天威[3]建立台风工况下“三塔两档线”的塔线耦联体有限元模型并对其进行静力学计算，表明塔线耦联作用不可忽略。雒亿平等[4]分析静力风载作用下的羊角形输电塔的轴力，发现输电塔主材承受的轴力大于辅材承受的轴力。丁志敏等[5]建立了“四塔五档线”模型，研究了塔线耦合体系的固有模态及振型，验证了导地线刚度小于铁塔构件刚度。卢银均等[6]建立了“两塔三档线”有限元模型，分析了塔线体系前300阶自振频率和振型，结果表明塔线体系在低阶模态时，导地线振动频率低于铁塔频率，在高频振动下主要以铁塔振动为主。于志强[7]建立了“两塔三档线”塔线体系的有限元模型，分析了其风振反应，认为输电线的存在增大了塔线体系的自振周期。谢文平等[8]建立了输电塔线体系的有限元模型，分析了塔线体系在强风作用下的风振响应，研究表明，随着高度的增加，输电塔峰值位移响应迅速增加，且横向振动明显大于纵向振动。Qin等[9]建立了双回路直线转角塔的有限元模型，对输电塔线系统的时域分析进行了研究，得到脉动风荷载对输电塔线系统的影响大于静风荷载对输电塔线系统的影响。Zhang等[10]建立了输电塔线耦合系统的有限元模型，分析了塔线系统的动力响应，结果表明，风速增大会使耦合效应逐渐变得显著，可能导致塔线系统有过早失效的风险。王彦海等[11]建立“两塔三档线”的有限元模型，分别对塔线体系在无风工况下的抗变形能力和设计风速工况下的动力响应进行分析，结果表明，风载荷会使输电塔线体系承受塔腿变形的能力明显降低。同时研究人员还进行了风致响应的静、动力学对比分析。裴慧坤等[12]建立了“三塔两档线”模型，对其进行动、静力学分析，认为动力响应情况下的应力、位移时程曲线指标均大于静力风荷载下的相应指标。唐磊等[13]建立了“三塔两档线”模型，计算了输电塔在随机风场中的动力响应及等效静力响应，动力学计算得到的主材、斜材应力均大于等效静力计算得到的结果。He等[14]建立了“三塔两档线”的有限元模型，对比进行了准静态分析和动力学分析，同样表明动态响应大于静态响应。虽然目前对输电线路风载作用下的力学性能研究已经有了一些进展，但对杆塔风致响应不同建模及加载方式的认识还不够全面。

为了系统研究输电铁塔风致响应中不同加载方式及耦合形式对杆塔的影响，现以500 kV输电线路中一酒杯型输电铁塔为中心的“一塔两档线”为研究对象，分别建立随机风载塔线分离、随机风载塔线耦合及等效静力风载三种有限元模型研究输电铁塔的力学性能，分析其位移与应力响应。分析结果可为研究输电塔线体系在风载荷作用下的力学性能以及后续诸如杆塔上的螺栓松动等不同问题时的模型选择提供参考。

1 塔线体系几何模型

1.1 塔线模型

研究对象为500 kV线路一典型耐张段，中间为酒杯型直线塔，塔高48.2 m，呼称高度为42 m，选取与两侧耐张塔的档距均为400 m。输电铁塔塔身主斜材为Q420、Q345钢，其余辅材为Q235钢，根据其杆件承载特点，采用空间杆梁混合单元建立其有限元几何模型。

输电导地线是一种柔性结构，只承受拉力，其刚度小、跨度大、非线性程度高。可以利用ABAQUS中不考虑压缩弹性模量的三维杆单元来模拟导线的索单元属性。该线路导地线参数如表1所示。

表1 导地线材料属性Table 1 Material properties of lines

1.2 金具模型

在研究输电铁塔风致响应时，线路上金具的细节对杆塔结果的影响可以忽略，在保证其等效质量和特征尺寸的前提下，可以简化其外部形状。I型、V型绝缘子串以及耐张绝缘子串模型均用圆截面梁模拟，截面半径为0.01 m，然后进行质量的等效。间隔棒采用边长为0.45 m的正方形模拟，相邻间隔棒之间的距离为20 m。

根据以上的建模方法，依次建立输电铁塔模型、导地线模型、绝缘子模型，组成“一塔两档线”的输电塔线体系模型，如图1所示。

图1 输电塔线体系模型Fig.1 Transmission tower-line system model

2 风载荷的计算

2.1 输电铁塔风载荷

输电塔不同高度处的风速不同，将铁塔的风载荷分8段计算，为了保证足够的安全裕度，取每个部分的最高点作为典型点，将典型点的风速用于整段部分的风载荷计算。具体分段情况如图2所示。

在B类地貌中，高度h处的风速Vh计算公式为

(1)

式(1)中：V10为离地10 m高的设计基准风速。

作用在与风向相垂直的输电塔的基本风压W0计算公式为

(2)

计算得到输电铁塔在不同高度位置的基本风压如表2所示。

图2 输电铁塔分段示意图Fig.2 Schematic diagram about each part of transmission tower

2.2 导地线风载荷

导地线在初始应力和重力影响下存在一定的弧垂，根据找形理论，导地线的空间位形为悬链线，经计算可得该档距下导地线的弧垂分别为11.58 m和8.05 m。

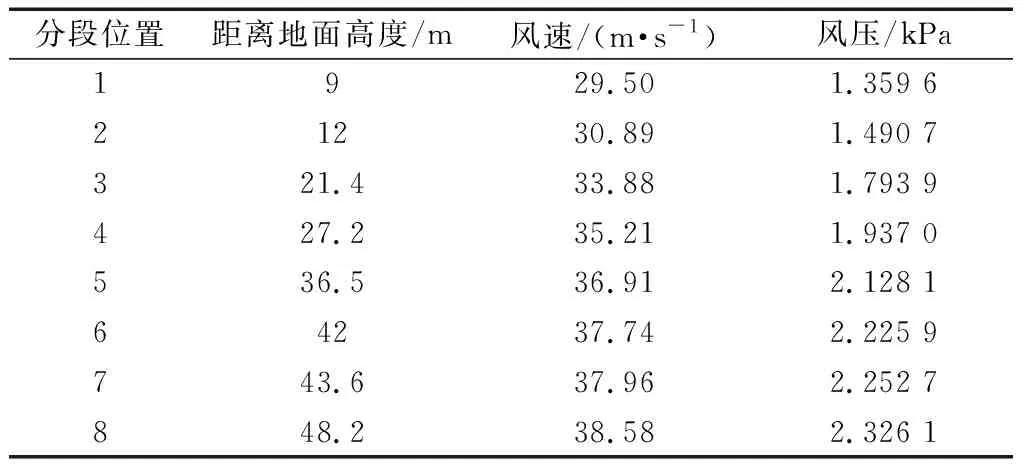
表2 输电铁塔不同位置处的风速与风压Table 2 Wind speed and pressure at different positions of transmission towers

考虑到导地线各点高度的差异对风速的影响较大，将档距400 m划分为50段，沿线路水平方向每隔8 m模拟一个风速样本，风模拟点的坐标选取每段导线的中点坐标。在模拟风速时，采用工程中广泛使用的Kaimal风速谱，模拟脉动风速时程样本。该输电线路所处地型为B类地貌，地面粗糙系数α取0.16，地面粗糙长度取0.03，模拟的总时长为120 s，时间步长为0.5 s，频率的截取范围为0.0～6.28 rad/s，频率范围等分数为3 000。模拟风场的设计基准风速为30 m/s。

图1中所示的第1、15、25三个模拟点的风速时程曲线如图3所示，将模拟得到的风速曲线进行谱分析得到功率谱S(ω)(ω为圆频率)，其与Kaimal谱对比结果如图4所示，可见模拟脉动风的风速功率谱与Kaimal谱吻合。

基本风速为30 m/s时点25风速的自相关函数R25，25以及点25与点1和点15的互相关函数R25，15、R25，1如图5所示，可以看出，距离越远，两点的相关性越低，与实际情况相符合。根据上述的分析，能够证明模拟风速时程样本的合理性。

根据中国电力行业标准，计算电线风载荷的表达式为

(3)

式(3)中：Wx为垂直于导线轴线的水平风载荷；α为风压不均匀系数；βc为500 kV线路风载荷调整系数；μsc为导线或地线的体型系数；d为导线或地线的外径；lH为杆塔之间的水平档距；θ为风向与导线或地线方向之间的夹角；μz为风压高度系数。

根据上述模拟的脉动风速及风载荷计算公式，便可计算得到对应导线、地线上的随机风载荷。

3 不同加载及耦合方式下的输电铁塔性能分析

3.1 塔线分离模型动力响应

塔线分离模型的建模过程：首先建立单独的两档400 m导线有限元模型，将两档线用悬垂绝缘子连接，并限制悬垂绝缘子串上端点的平动自由度；导线两端各连接一个耐张绝缘子串，耐张绝缘子串外侧端点只具有绕导线方向的旋转自由度；最后对导线施加2.2节中模拟得到的脉动风载荷，进行动力学分析得到悬垂绝缘子串上端点的支反力时程曲线，地线支反力的提取与导线类似。

图3 模拟点的风速时程曲线Fig.3 Wind speed time history curve at simulated points

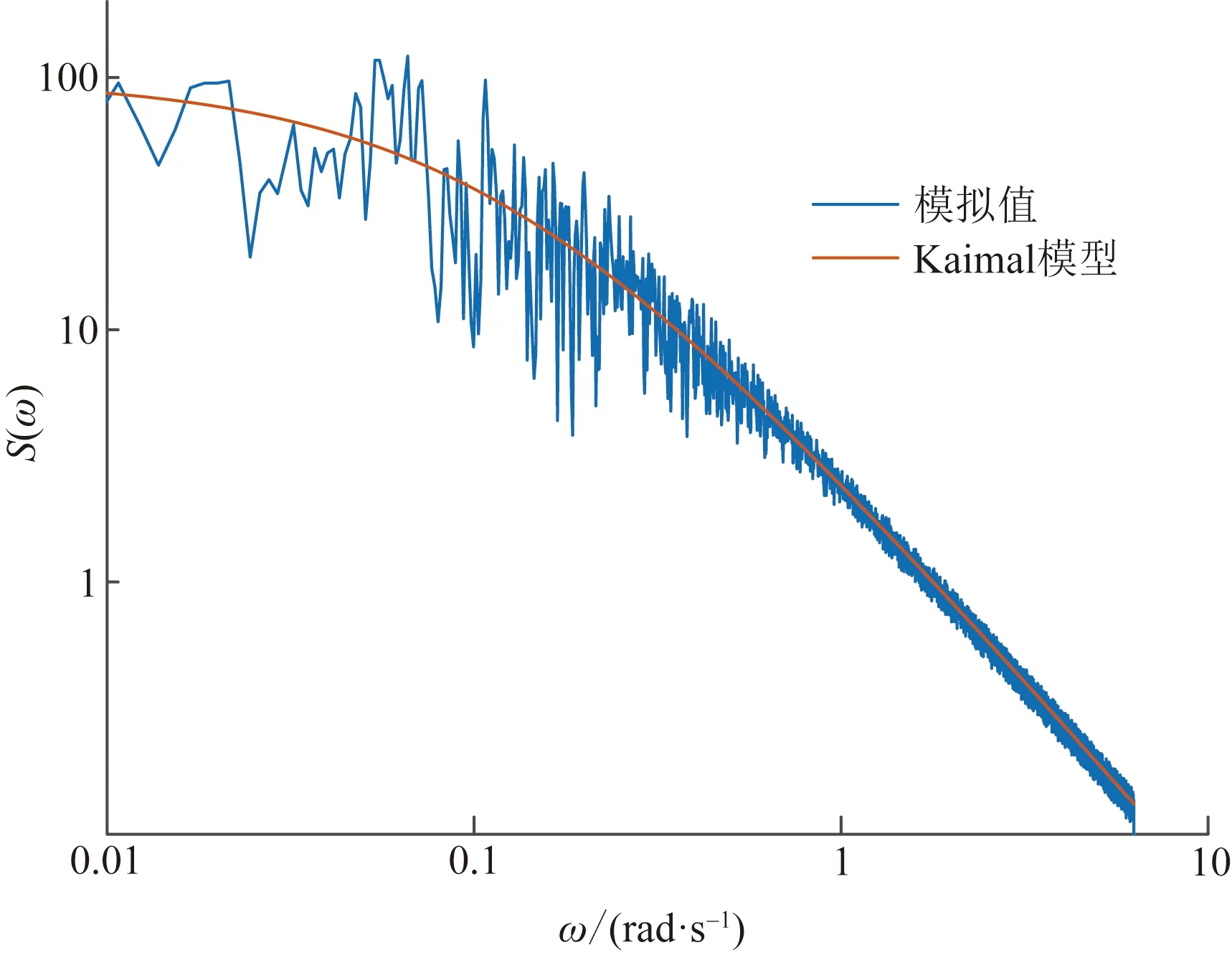
图4 模拟脉动风速功率谱与Kaimal谱的对比Fig.4 Comparison between simulated fluctuating wind speed power spectrum and Kaimal spectrum

图5 第25点模拟风速的自相关函数及与 代表点风速的互相关函数Fig.5 Autocorrelation function of point 25 simulated wind speed and the cross-correlation function with the wind speed of representative points

将导地线绝缘子串各端点提取的支反力以相互作用力的形式施加到挂点上，可以模拟导地线对输电铁塔所带来的影响。同时根据表2中的风压数据，对输电铁塔各部分施加相应的风载，并对塔脚施加固定约束，然后进行动力学分析。输电铁塔杆件在迎风面受到拉力作用，背风面受到压力作用。如图6所示为t=12.82 s时刻的铁塔应力和位移分布情况，可见该时刻除了塔脚应力集中外，应力最大值出现在塔身第二部分的主材上，为209.19 MPa，这与大多数受风倒塌的铁塔破坏位置是吻合的，在设计过程中应引起特别关注。位移作为最直观的输出，是判断铁塔变形程度的重要依据，由图6(b)可知，最大位移出现在塔头处，为280.77 mm。

3.2 塔线耦合模型动力响应

塔线耦合模型是将输电铁塔和导地线耦合为一个系统，同时对导地线和塔身施加相应的风载荷。塔线耦合模型的塔脚以及耐张绝缘子串处的边界条件与塔线分离模型完全一致。不同之处体现在悬垂绝缘子串通过“Join + Rotation”连接器与挂点相连，不再单独设置其边界条件[15]。同样对该系统进行120 s动力学计算，t=12.33 s时刻的塔线耦合系统受风载荷作用下的变形示意图如图7所示。对比塔线分离模型，应力危险区域位于同一位置，应力最大值为211.13 MPa，位移最大值位置依然位于塔头处，值为284.01 mm。

图6 塔线分离模型铁塔应力与位移值分布Fig.6 Stress and displacement distribution diagram of tower-line separation model

3.3 等效静力风载荷响应研究

无论塔线分离还是塔线耦合模型的计算都会消耗大量的建模以及计算时间，尤其是在计算多种风速、风向角等不同影响因素的情形下。为了提高效率，采用等效静力加载的方式研究输电铁塔的风致响应。

图7 风载荷作用下的塔线耦合模型变形示意图Fig.7 Deformation diagram of tower-line coupling system under wind load

将导线和地线所受的风载荷等效为静力作用，相应的静力风载荷计算公式为

Wx=αμscβcdlHW0sin2θ

(4)

式(4)中：W0为基本风压。根据计算，可得在30 m/s设计基准风速、90°风向角工况下的四分裂导线上的等效静力风载荷为33.32 kN，地线上的等效静力风载荷为4.90 kN。

输电铁塔的边界条件与塔线分离模型一致，只有塔脚位置设为固定约束，忽略塔线之间振动的相互影响，将等效静力风载荷直接施加到挂点上，塔身仍然考虑风载荷作用，然后对其进行静力学分析。应力危险区域仍然出现在输电铁塔的第2部分的相同位置，应力值为183.97 MPa，最大位移值的位置出现在塔头处，位移值为261.74 mm。

3.4 不同加载及耦合方式下结果对比

分别提取塔线分离、塔线耦合及等效静力模型响应结果，其中塔线分离及耦合模型的塔身危险位置的应力与位移时程曲线如图8所示。

由图8可知，塔线耦合与分离情况下的应力与位移响应的变化趋势基本一致，对应的数值相差很小。但是由于塔线耦合效应的存在，使得输电铁塔的应力分布以及位移响应频繁波动，杆件所承受的交变载荷会对其安全性能产生影响。

三种不同计算模型的应力危险区域均相同。塔线分离和耦合模型采用的动力学计算方法，其危险区域的应力和位移最大值以及稳定后的平均值、等效静载模型相同位置的力学性能如表3所示。

图8 塔身危险位置的应力与位移时程曲线Fig.8 Time history curves of stress and displacement at the dangerous position of the tower

表3 三种模型结果对比Table 3 Comparison between three models

可见，风载荷导致的杆塔力学性能动力学计算指标均大于静力学效应的相应指标。在研究输电铁塔杆件屈服等问题时，等效静力风载荷的应力响应不能作为判断依据。同时注意到等效静载模型的最大位移值是小于动力学计算结果的，这是由于等效静力时并未考虑导地线重力和塔线耦合的影响。但是等效静力风载荷模型计算得到的应力值非常接近动力学计算的平均值，可以作为快速近似估计其动力风载荷平均应力响应的一种途径。相较于其他两种模型，等效静载模型计算效率高，可用于后续计算构件的轴力变化进而评估螺栓连接松动特性研究。

4 结论

建立了500 kV线路耐张段“一塔两档线”分离、耦合动力学模型以及等效静力学模型。分别计算输电铁塔和导地线的随机风载及等效静载，并施加到相应的模型上，对其应力和位移响应进行对比分析。

(1)三种计算模型均显示危险区域位于塔身主材上，通过对比塔线分离模型和塔线耦合模型的杆塔力学性能可知，由于塔线耦合效应的存在，使得输电铁塔的应力分布以及位移响应频繁波动，其承受的交变载荷会对其安全性能产生影响。

(2)塔线系统动力学模型得到杆塔上的应力和位移最大值均大于等效静力风载荷模型，动力学分析在评估杆塔性能时不可忽略。

(3)等效静载模型计算效率高于其他两种模型，可用于快速近似估计其动力风载荷平均应力响应，也可用于后期杆件的轴力计算，快速评估螺栓的横向载荷。