致密砂岩气井气水两相产能预测半解析模型

王苏冉， 白玉湖， 徐兵祥， 李彦尊， 陈岭， 董志强

(中海油研究总院有限责任公司， 北京 100028)

近年来，中国致密砂岩气藏展现出了丰富的资源前景，在弥补常规油气产量短缺中扮演日益重要的角色。致密砂岩储层通常物性较差，主要通过水力压裂技术实现对储层大规模体积改造，以此获得经济开采效益。李小龙等[1]、方文超等[2]研究表明水力压裂往往产生复杂的缝网改造体，缝网改造程度是制约致密气井产能的主要因素之一。另外，致密砂岩储层一般具有较高的初始含水饱和度，在开发过程中极易出现气水两相流特征，导致部分气井产水问题比较突出，影响气井产能发挥[3-5]。此外，李跃刚等[6]、丛海龙等[7]、王欣等[8]通过实验和理论研究发现致密砂岩储层具有一定的应力敏感性，应力敏感效应对气水渗流能力有严重的负面作用，直接影响气井的稳产能力。因此，压裂缝网参数、气水两相流特征以及储层应力敏感效应是影响致密气井产能准确预测的关键因素，产能评价模型中应着重考虑。

目前，致密砂岩气井产能预测方法主要包括解析、半解析和数值模拟方法。解析方法通常以稳态渗流理论为基础，建立致密气井产能计算模型。张楠等[9]、杨兆中等[10]基于稳态渗流理论，运用点汇法以及势的叠加原理推导了致密气压裂水平井产能计算模型。丁景辰[11]考虑了应力敏感的影响，建立了两区复合模型。对于致密砂岩气藏而言，其开发过程长期处于非稳态流动阶段，基于稳态渗流理论建立的产能方程不能真实反映气藏生产过程。半解析方法[12]主要是基于线性流假设建立起来的，该方法能够有效刻画缝网改造体，同时计算方便，得到了广泛的应用。然而，这些解析和半解析方法仅适用于单相流体的产能预测，对于致密气开发过程中出现的气水两相流，由于数学模型本身严重的非线性，以上模型不再适用。何吉祥等[13]、袁淋等[14]通过引入气水两相拟压力将方程线性化，并利用保角变换和势的叠加原理推导产水气井产能方程，将产水量折算成产气量进行评价。该方法在处理气水两相渗流方程非线性问题时通常仅引入两相拟压力将方程简化求解，忽略非线性渗流参数的影响，计算结果误差大。李波等[15]、宋海敬等[16]、Wu等[17]建立了致密砂岩气压裂井数值模型，该方法能够显式表征人工裂缝参数特征，处理多相流体流动问题，但前处理过程复杂，为了获取较高的模拟精度，需要对裂缝进行网格加密处理，导致网格数量庞大，在处理成千上万个案例分析时，计算时效性较低。总之，致密砂岩气井产能准确预测的难点主要表现在：一是在水力压裂形成的缝网模拟困难；二是气水两相流动以及应力敏感模拟困难。

现利用三线性流模型对缝网改造体进行表征，建立致密砂岩气藏直井压裂气水两相产能预测模型，并研究一种高效的求解方法处理气水两相流动和应力敏感引起的非线性渗流问题。首先通过引入两相拟压力和拟时间将渗流方程归一化，并利用Laplace变换等方法获得初始时刻模型的解析解；然后结合流动物质平衡和牛顿迭代法，利用不同时间下的平均地层压力和饱和度更新模型非线性渗流参数，逐步实现渗流模型的线性化，以此获得模型的半解析解。通过与商业数值模拟软件对比验证模型的准确性，并基于研究的半解析模型分析裂缝及储层关键渗流参数对产能预测的影响，而后开展实例井产能预测与分析工作。

1 模型的建立

1.1 物理模型

利用三线性流模型表征压裂改造体，流体流动划分为3个区域：内区裂缝线性流动、地层流体垂直于裂缝的线性流动以及外区流体平行于裂缝的线性流动[18]，如图1所示。模型假设人工压裂缝与井筒直接相连，且流体仅通过裂缝流入生产井筒，基质中流体不断向裂缝流动，提供能量补给。考虑气水同产，基质和裂缝中均为气水两相流动，且符合等温达西渗流。其他物理模型假设条件为：①储层顶部、底部和侧向均为封闭边界；②储层全部压开，压裂裂缝与井筒对称；③与气体相比，地层水的压缩系数较小，可以忽略；④考虑储层渗透率应力敏感性；⑤不考虑重力和毛管力的影响。

pw为井筒压力，MPa；pF为人工裂缝中压力，MPa；I为内区(改造 区)；II为外区(未改造区)；xF为裂缝半长图1 致密砂岩气藏压裂直井模型流动示意图Fig.1 Schematic diagram of fractured well model in tight sandstone gas reservoir

1.2 数学模型

基于物理模型假设，分别对各个流动区域建立渗流数学模型，为方便推导，通过引入无因次变量简化数学模型的形式，无因次参数定义如下。

式中：pD为无因次压力；ψD为无因次拟压力；tD为无因次时间；taD为无因次拟时间；qgD为无因次产气量；qwD为无因次产水量；ηD为无因次导压系数；CFD为无因次裂缝导流能力；xD、yD、zD为无因次长度(x、y、z坐标方向)；wFD为无因次裂缝宽度；kFD为无因次裂缝渗透率；p为压力，MPa；pi为原始地层压力，MPa；pwf为井底流压，MPa；ψ为拟压力，MPa2/(mPa·s)；ψi为原始地层拟压力，MPa2/(mPa·s)；ψwf为拟井底压力，MPa2/(mPa·s)；t为时间，d；ta为拟时间，d；T为温度，K；kr为参考渗透率，mD；kF为裂缝渗透率，mD；kmi为初始时刻基质渗透率，mD；qg为产气量，万m3/d；qw为产水量，m3/d；Lr为参考长度，取裂缝半长，m；H为储层有效厚度，m；wF为裂缝宽度，m；Bw为地层水体积系数，m3/m3；μw为地层水黏度，mPa·s；ηiD为无因次导压系数，j=F表示裂缝，j=m表示基质。

引入拟压力和拟时间，分别定义为

(1)

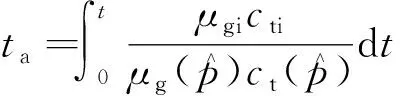
(2)

1.2.1 外区基质系统气水两相无因次渗流数学模型

气相流动方程采用拟压力和拟时间处理，其控制方程为

(3)

式(3)中：ψm2D为外区无因次拟压力；kmrg为基质系统中气相相对渗透率；ηmD为基质系统中气相的无因次导压系数。

初始条件：ψm2D(xD,taD)|taD=0=0。

内边界条件：ψm1D(xD,taD)|xD=1=ψm2D(xD,taD)|xD=1。

水相流动方程采用真实时间处理，其无因次控制方程和边界条件为

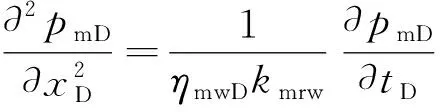
(4)

内边界条件：pm1D(xD，tD)|xD=1=pm2D(xD，tD)|xD=1。

式(4)中：ψm1D为内区无因次拟压力；kmrw为基质系统中水相相对渗透率；ηmwD为基质系统中水相的无因次导压系数；pm1D为内区无因次压力；pm2D为外区无因次压力。

1.2.2 内区基质系统气水两相无因次渗流数学模型

气相控制方程为

(5)

初始条件：ψm1D(yD，taD)|taD=0=0。

内边界条件：ψm1D(yD，taD)|yD=wFD/2=ψFD。

水相控制方程为

(6)

初始条件：pm1D(yD，tD)|tD=0=0。

内边界条件：pm1D(yD，tD)|yD=wFD/2=pFD。

1.2.3 人工裂缝系统气水两相渗流数学模型

气相控制方程为

(7)

初始条件：ψFD(xD，tD)|tD=0=0。

定压生产内边界条件：ψFD(xD，tD)|xD=0=1。

水相控制方程为

(8)

定压生产内边界条件：pFD(xD,tD)|xD=0=1。

式中：ψFD为人工裂缝系统无因次拟压力；kFrg、kFrw分别为人工裂缝系统中气相和水相相对渗透率；ηFD、ηFwD分别为人工裂缝系统中气相和水相的无因次导压系数。

2 气水两相产能预测半解析解

将生产时间离散为多个时间步，在每个时间步，与压力相关的参数(μg、Bg)以及与饱和度相关的参数(kmrg、kmrw、kFrg、kFrw)分别由动用范围内的平均压力和平均饱和度更新替换，因此，非线性参数在每个时间步可以当作定值近似处理。在处理了非线性渗流问题后，每一时间步的气相和水相产量可通过直接求解方程获得。

2.1 气相流动方程求解

对每个流动区域的气相渗流方程取关于无因次拟时间的Laplace变换，与单相模型求解过程类似，首先对外区基质系统气相渗流方程进行Laplace变换，其通解为

(9)

对内区基质系统气相渗流方程进行Laplace变换，可得其通解为

(10)

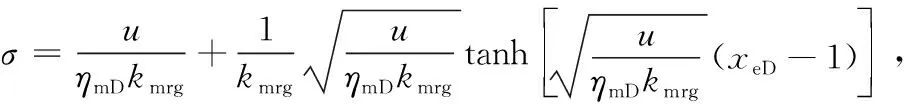
对人工裂缝系统气相渗流方程进行Laplace变换，可得其通解为

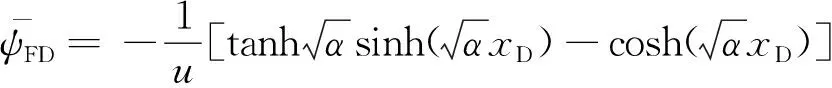
(11)

单井产气量表达式为

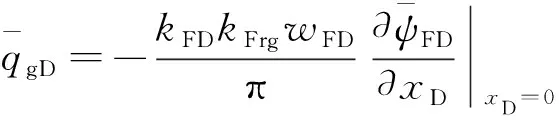
(12)

结合式(12)，可得气相产量的解为

(13)

式(13)中气相产量的解是在Laplace空间求得的，利用Stehfest[19]数值反演即可得到实空间的解。

2.2 水相流动方程求解

对每个流动区域的水相渗流方程取关于无因次时间的Laplace变换，与气相渗流模型求解过程类似，对外区基质系统水相渗流方程进行Laplace变换，其通解为

(14)

对内区基质系统水相渗流方程进行Laplace变换，可得其通解为

(15)

对人工裂缝系统水相渗流方程进行Laplace变换，可得其通解为

(16)

结合式(13)，可得水相产量的解为

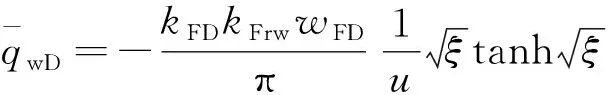
(17)

式(13)和式(17)中仍然存在与压力和饱和度相关的参数，此外，式(18)给出了考虑应力敏感的渗透率表达式，将应力敏感项全部整合到导压系数中，并作为平均地层压力的函数[20]。在模型求解过程中，利用动用范围内的平均地层压力和饱和度更新每个时间步的非线性参数，逐次迭代获得模型的解，而平均地层压力和平均饱和度由流动物质平衡方法计算获得，表达式为

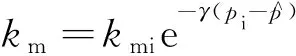
(18)

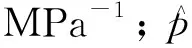
2.3 流动物质平衡方程的建立

气相物质平衡方程为

(19)

整理式(19)可得

(20)

内区沿裂缝方向以及垂直裂缝方向的动用范围[21-22]分别为

(21)

水相物质平衡方程为

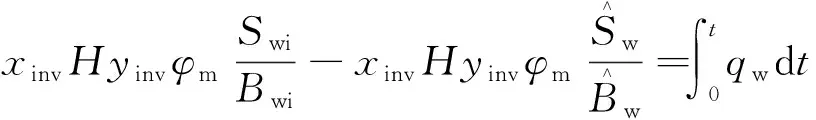
(22)

对式(22)进行整理可得

(23)

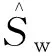
饱和度满足如下关系

(24)

联立式(20)、式(23)和式(24)，构建平均压力函数，有

(25)

式(25)中：

对式(25)求导，有

(26)

由式(26)构建平均压力牛顿迭代格式，有

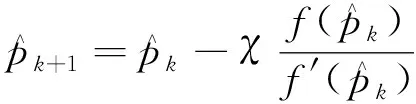
(27)

式(27)中：k为上一时间步，k+1为当前时间步；χ为迭代因子，取1/2k。

运用牛顿迭代获得平均压力，然后代入式(20)、式(23)可计算平均饱和度。利用动用范围内的平均压力和饱和度更新每一时间步下的非线性参数，逐步迭代计算可获得致密砂岩气井气水两相渗流模型的解，进而可编程绘制气水两相产能曲线，预测气水生产动态。

3 气水两相生产动态分析

3.1 模型验证

为验证所提出的半解析模型的准确性，利用Eclipse软件建立了如图2(a)所示的数值模型，井名为PROW。模型使用的气体高压物性参数关系曲线如图2(b)所示。表1为两种方法使用的储层及裂缝参数，图3为储层及裂缝中的气水两相相对渗透率曲线。本算例中基质和裂缝系统均考虑气水两相，即在生产初期便发生气水两相流。

半解析模型和Eclipse的对比结果如图4所示，可见，两种方法获得的产量曲线在生产早期存在一定差异，在后期结果基本一致。相同储层与裂缝参数条件下，气水两相渗流条件下的产能明显低于单相渗流。这主要是因为在生产早期，近井地带压力和饱和度变化大，而生产对压力和饱和度相关的参数很敏感，在半解析模型中，利用拟压力隐式地处理部分与压力相关的参数，但饱和度相关的参数作显式处理，所以单相渗流模型早期的误差不明显，两相流模型早期的误差较明显，但是计算得到的平均相对误差小于10%，在工程允许误差范围之内，说明提出的半解析模型可用于生产数据的分析和预测。相比于数值模拟方法，本文方法计算速度快，更加有利于矿场大规模案例分析应用。

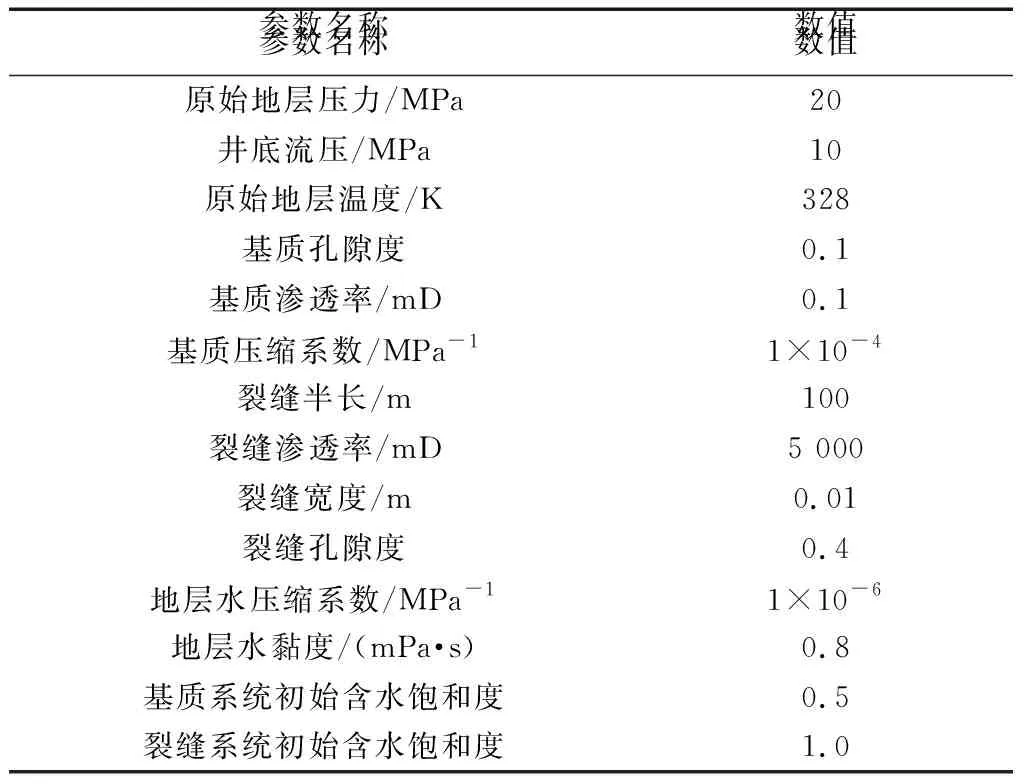
表1 模型验证输入参数Table 1 Input parameters for model validation

图2 Eclipse模型示意图和气体高压物 性参数关系曲线Fig.2 Schematic of the Eclipse model and gas PVT properties

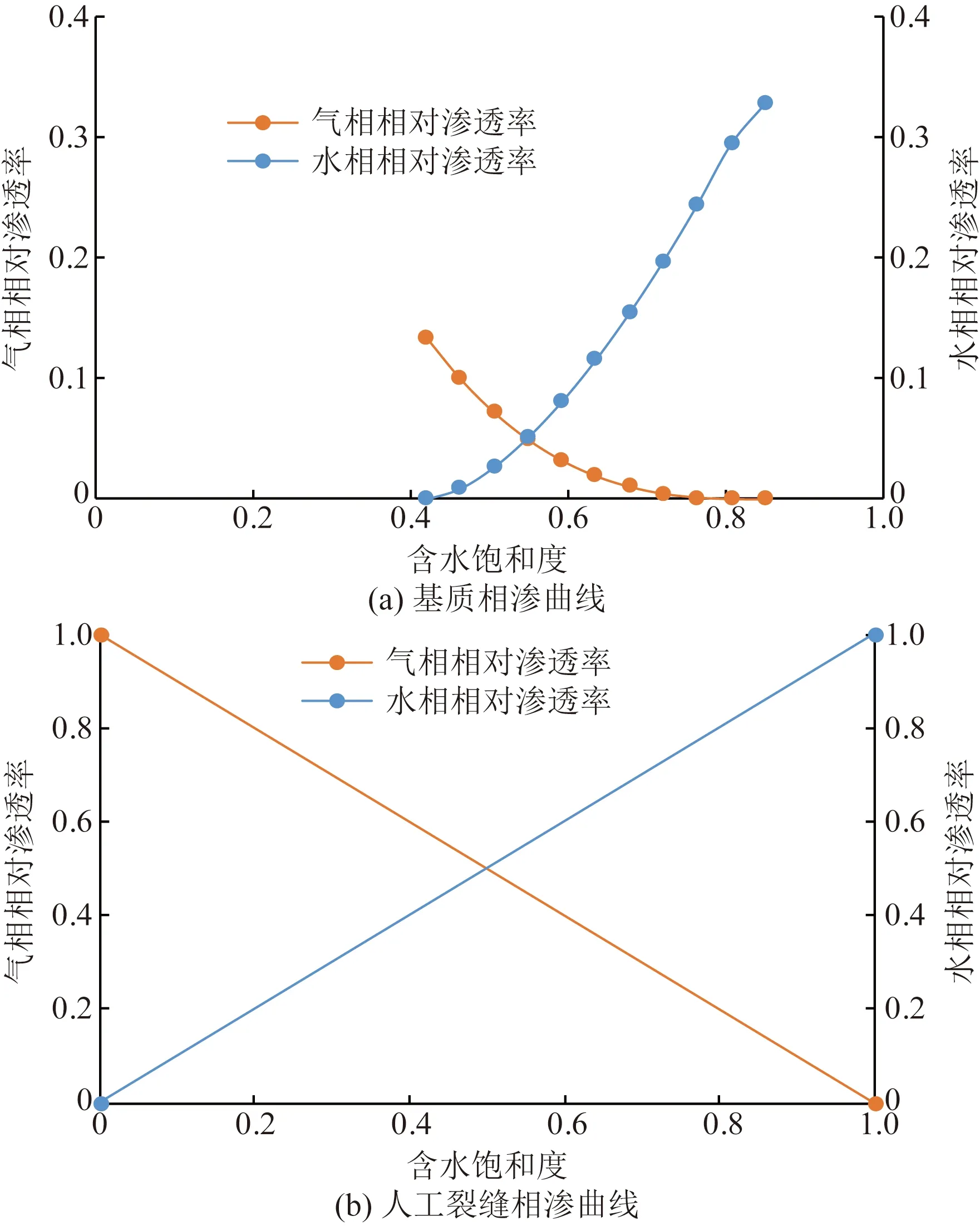
图3 基质系统和人工裂缝系统相对渗透率曲线Fig.3 Relative permeability of the matrix system and hydraulic fracture system

图4 本文模型和Eclipse对比结果Fig.4 Comparison of gas and water production rate between the semi-analytical model in this paper and the Eclipse

3.2 生产动态影响因素分析

致密砂岩储层自然产能低，而压裂改造是提高致密气井产能的关键，基于研究的半解析模型，首先分析了人工压裂缝导流能力、裂缝半长对致密气井产能的影响规律，然后基于储层渗流机理实验研究结果，分析了储层物性和应力敏感性对气水两相产能的影响。敏感性参数取值范围如表2所示。

图5和图6分别反映了裂缝导流能力(CF)和裂缝半长(xF)对致密气井气水两相产能的影响。从图5可以看出，裂缝导流能力越大，产量初值越大，同时产量递减趋势越缓慢。这主要是因为裂缝导流能力越大，产量越大，在定井底流压生产条件下，通过较小的产量递减量就可以维持生产。从图6可以发现，裂缝半长的变化影响着整个开发阶段，尤其对早中期生产阶段影响较大，且随着裂缝半长增加，气相产量增加，但是增加的幅度逐渐变小。这主要是因为裂缝半长不仅能够表征储层改造体积的大小，同时反映了井控储量和动用范围，其值越大，裂缝线性渗流面积越大，动用范围越大，因此产量越大，产量递减越缓慢。

表2 敏感性参数取值范围Table 2 Range of values for sensitive parameters

图5 裂缝导流能力对产能的影响Fig.5 Effects of fracture conductivity on gas and water production rate

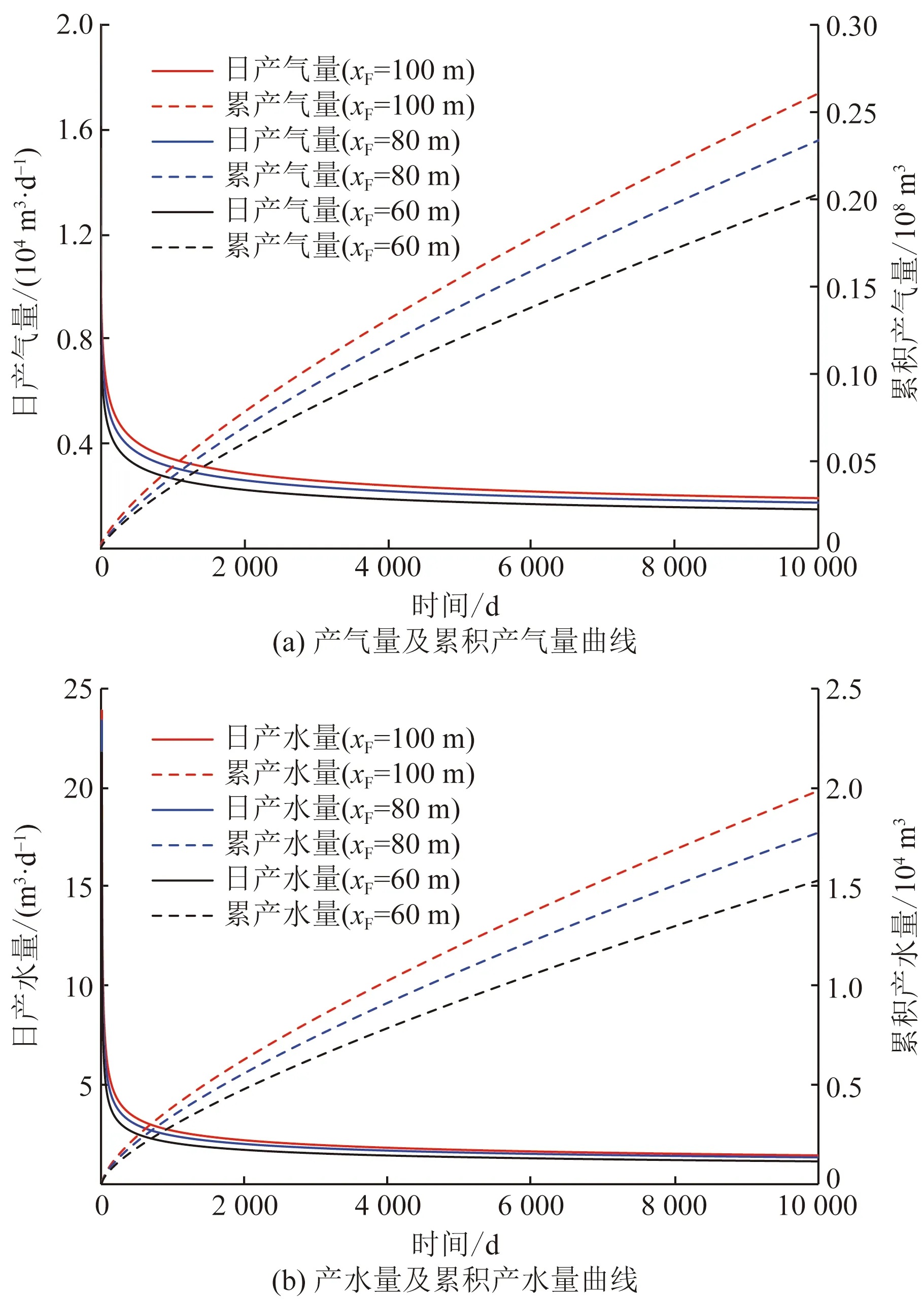
图6 裂缝半长对产能的影响Fig.6 Effects of fracture half-length on gas and water production rate

图7和图8分别反映了储层渗透率(km)和渗透率模量(γ)对致密气井气水两相产能的影响。从图7可以看出，储层渗透率越大，气水两相产量初值越大，由于基质向裂缝供给和渗流能力变强，产量递减趋势减缓。从图8可以发现，应力敏感效应影响整个致密气藏的开发过程，尤其对早、中期生产阶段影响较大，且生产压差越大，渗透率损失越严重，流体渗流阻力增加，最终导致产量降低，且递减速度加快。因此，对于致密气藏而言，在生产过程中应保持合理的生产压差降低应力敏感效应对产能的影响。

3.3 案例分析

以鄂尔多斯盆地一口产水致密气井为例说明该模型的应用效果。该井于2015年2月压裂投产，储层的初始含水饱和度约为50%，截止到2020年6月累积产气2 313×104m3，累积产水2 078 m3，日产气量9 720 m3/d，日产水量1.3 m3/d。该井基础数据如表3所示，气体的PVT关系曲线以及气水相渗曲线分别如图2(b)和图3所示。利用本文模型对该井气水两相生产数据进行拟合解释，如图9所示。可见，理论曲线和实测曲线拟合效果较好，虽然拟合结果存在一定的偏差，但在工程误差允许范围之内。将该井拟合解释结果汇总于表4，其中，解释的裂缝导流能力为80 mD·m，裂缝半长为95 m，储层渗透率为0.5 mD，储层应力敏感系数为0.04 MPa-1，均与气藏实际相符。对该井的产量进行预测，生产30年采出气量为7 870×104m3，采出水量为2.4×104m3。

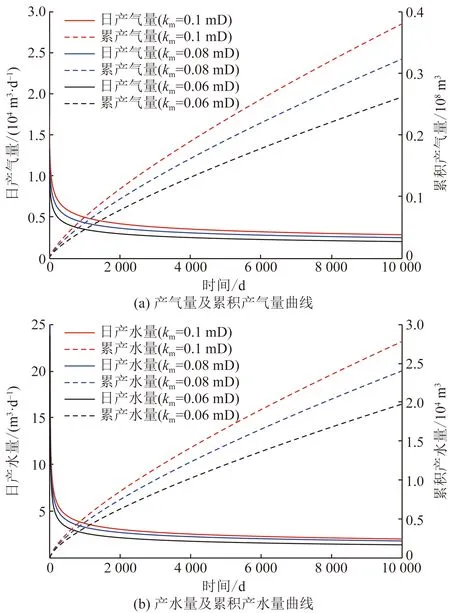
图7 储层渗透率对产能的影响Fig.7 Effects of reservoir permeability on gas and water production rate

图8 储层应力敏感效应对产能的影响Fig.8 Effects of stress sensitivity of reservoir on gas and water production rate

表3 矿场实例分析输入参数Table 3 Input parameters for field case study

表4 实例井拟合解释结果Table 4 The fitting results of an example well

图9 实例井产量递减解释与预测Fig.9 Rate decline analysis and prediction of an example well

4 结论

建立了考虑储层复杂裂缝、应力敏感效应及气水两相渗流特征的产能模型，并结合流动物质平衡方法建立了模型的半解析求解方法，实现了致密气井气水两相的产能预测，主要结论如下。

(1)利用流动物质平衡方法计算储层的平均压力和平均饱和度，并逐次更新渗流模型中的非线性参数，能够较为准确地处理气水两相非线性渗流问题，从而实现渗流模型的高效准确求解。

(2)数值模型验证结果以及矿场应用均表明本文方法预测精度高，可以用于致密气井气水两相产量的预测。

(3)裂缝关键渗流参数对气水两相生产动态起着重要的影响作用。由于致密气藏产水严重影响了气井产能，相同储层与裂缝参数条件下，气水两相渗流条件下的产能明显低于单相渗流条件下的产能，因此，针对气水同产致密气井，在压裂施工时应尽量增加改造程度和范围来提高气井产能。

(4)储层应力敏感效应影响致密气井产能，生产过程中需要合理地控制生产压差以有效降低应力敏感效应的负面影响。