混凝土非均匀性对超声波衰减作用的模拟分析
张文亮, 辛公锋, 宋雷, 龙关旭
(1. 山东高速集团有限公司创新研究院, 济南 250098; 2. 山东省高速公路技术和安全评估省级重点实验室, 济南 250098; 3.中国矿业大学深部岩土力学与地下工程国家重点实验室, 徐州 221116)
混凝土是土木工程中最常用的复合材料之一,被广泛应用于桥梁、隧道、井壁、墙体等现代基础设施中,随着服务年限的不断增加,结构设施的运营和维护变得非常复杂,在自然灾害、风化侵蚀、应力疲劳、不定荷载等作用下,混凝土结构不可避免地出现诸如裂缝、空洞、腐蚀等不同程度的损伤,混凝土结构的完整性和力学性能测试是保证基础设施安全可靠运行的关键。超声波的传播对混凝土的组成和力学性能非常敏感,并且具有探测精度高、检测成本低、设备便携等优势,因此被视为混凝土损伤检测和性能评估最具潜力的无损检测方法之一[1-4]。
颜华等[5]测试了超声波在缺陷混凝土构件中声波、声幅、波形和频率等参数的变化规律,以此判断混凝土结构是否存在缺缺陷。于函等[6]通过正交试验研究了超声波波速与透水混凝土性能(孔隙率、干密度、渗透系数、抗压强度、抗折强度与抗冻等级等)之间的关系,为基于超声波波速评价透水混凝土各项基本性能及冻融损伤程度提供了理论依据。肖楚珺等[7]研究发现在碾压混凝土凝结过程中,各阶段的超声波频谱特征不同,基于此特征参量可以快速判断碾压混凝土的凝结状态。Asadollahi等[8]在将骨料简化为椭球体和立方体的基础上,模拟研究了骨料的形状、粒径和声阻抗等参数对超声波能量衰减的影响,结果显示骨料形状对超声波的衰减影响不大,而骨料的声阻抗和粒径越大,造成的散射衰减越大。在实际生产中,骨料的选材通常较为单一,而水泥砂浆则因为配合比设计的不同,其声学参数变化范围很大,因此将水泥砂浆材料的声阻抗等参数作为变量更具实际意义。另外试验研究表明,在动静荷载作用下,混凝土均会表现出黏弹性质[9-11],黏弹性对波在介质中传播的动力学特性,特别是波能的衰减起着重要作用。因此除散射作用外,黏弹性作用下的固有吸收也是超声波能量衰减需要考虑的重要因素。Nakahata等[12]引入黏弹性模型,用以表征混凝土对超声波的固有衰减作用,模拟了400 kHz超声波在混凝土中的传播,研究发现散射衰减是造成超声波能量衰减的主因。朱自强等[13]建立了椭圆形骨料的数值混凝土模型,基于黏弹性声波方程模拟了100 kHz和200 kHz超声波的传播,通过比较超声波在均匀介质、水泥砂浆和混凝土中的衰减,结果表明混凝土的黏弹性会导致超声波能量随传播距离的增大呈指数衰减,是超声波能量衰减的主因之一。另外在Nakahata的研究中,通过比较超声波在骨料体积比为10%、30%和50%的混凝土中的衰减发现,超声波的最大振幅随骨料体积呈递减趋势。而密士文[14]的研究发现,超声波在骨料体积比为30%和75%的混凝土中的衰减差别不大,分析认为骨料含量的增多,虽然在一定程度上导致散射衰减增大,但也提高了超声波的传播速度,降低了几何扩散衰减,综合的结果为骨料含量的变化对超声波能量的衰减影响不大。顾兴宇等[15]研究了集料粒径和温度对沥青混凝土中超声波衰减特征的影响,从而形成了沥青混凝土超声波检测频率的建议。综上可见,受限于研究目的和研究方法的不同,得到的研究结果存在较大差异。此外,在相同介质中不同入射频率的超声波对应了不同大小的波长,波长与非均质体的相对大小决定了超声波的传播特征,因此作为超声波检测的关键技术参数,入射频率是影响检测结果的主要因素。
超声波的运动学和动力学特征对混凝土的组成和力学性能非常敏感,是实现混凝土质量检测的基础。但是由于混凝土自身强烈的随机非均匀性对超声波传播的扰动,导致混凝土性能参数和超声波传播参数之间并非简单的线性关系,因此深入探究混凝土随机非均匀性对超声波传播参数的影响,是准确提取有用信号、实现混凝土质量准确评价的关键。为了进一步研究混凝土随机非均匀性对超声波的衰减作用和影响因素,现基于数字图像处理技术提取真实的混凝土结构,采用实测的混凝土细观组分声学参数,在定量表征混凝土细观组分参数的基础上,研究骨料粒径、骨料含量、水泥砂浆速度和品质因子等参量对超声波频率和能量衰减的影响。研究成果对于混凝土结构的超声波无损检测参数的优化和检测结果的可靠性解释提供依据,具有重要的工程指导意义。
1 超声波基本控制方程
为了考虑混凝土黏弹性对超声波传播的影响,引入Kelvin-Voigt模型表征混凝土的非弹性本构关系。如图1所示,通过将黏弹性体视作弹簧和阻尼器的并联组合,能够在不引入附加场变量的情况下,表征介质的非弹性本构关系。
根据各向同性弹性介质的物性参数与Kelvin-Voigt黏弹性介质物性参数的对应规则[16]:λ↔λ+λ′∂/∂t和μ↔μ+μ′∂/∂t,可以估算黏弹性介质的应力和应变关系。据此得到开尔文黏弹性介质的一阶速度-应力波动方程为
σ1=με
(1)
(2)

σ1和σ2分别为作用在黏弹性体上弹性应力部分和黏性应力部分;μ为弹簧的弹性系数;η为阻尼器的黏滞系数;σ为总应力, 则有σ=σ1+σ2;ε为总应变图1 Kelvin-Voigt黏弹性体示意图Fig.1 Diagram of Kelvin-Voigt viscoelastic body
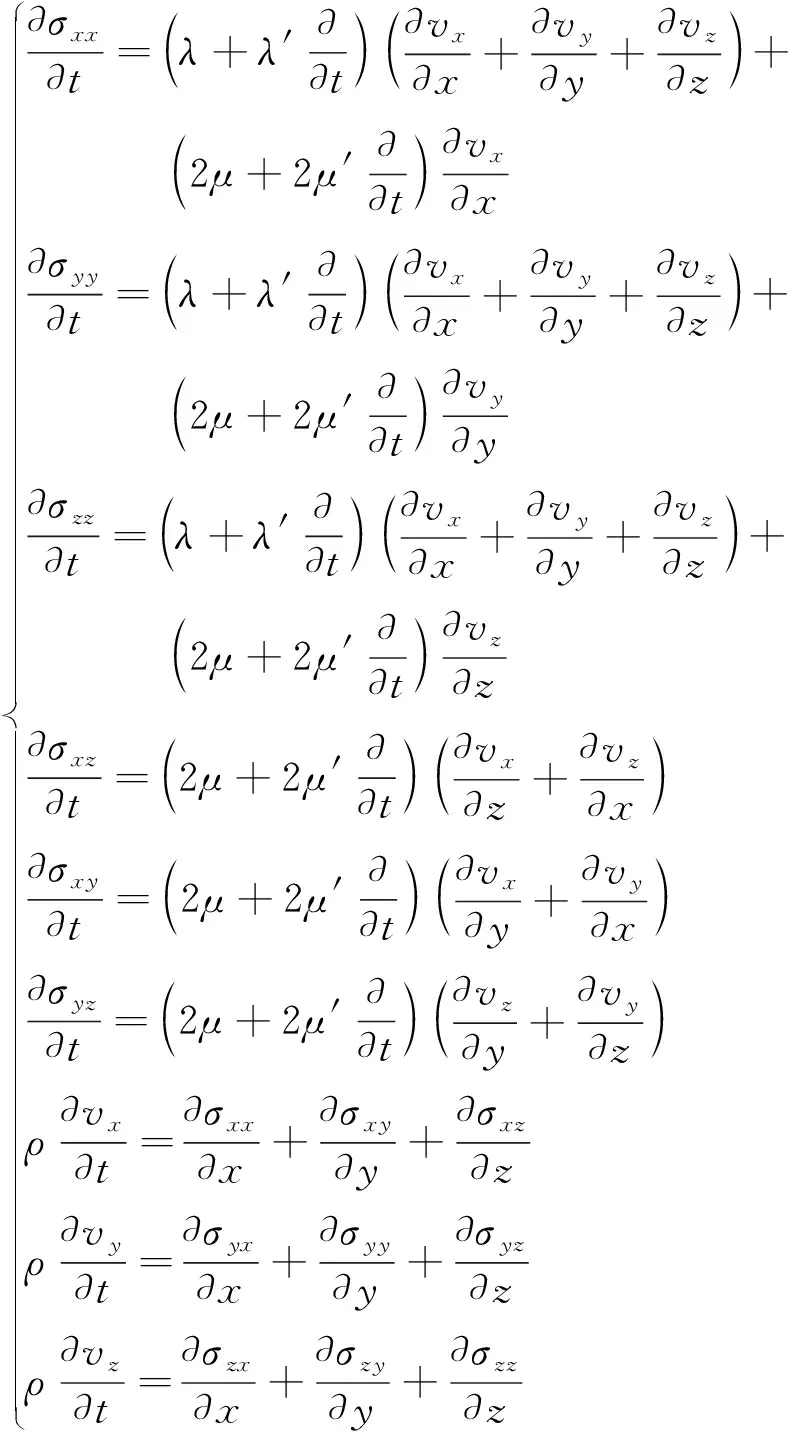
(3)
介质的拉梅系数与超声波在介质中传播速度的关系可以写为
(4)
式(4)中:Vp、Vs分别为纵波和横波;Qp、Qs分别为纵波和横波的品质因子;w为角频率。
为了简化研究,这里忽略横波以及各种转换波的影响,令声压P表示应力σxx和σzz,给出二维黏弹性声波方程的一阶速度-应力方程形式为
(5)
采用时域有限差分法求解声波方程,模拟超声波在混凝土中的传播。采用完美匹配层吸收边界条件消除模型边界反射,为了尽量最小化数值频散和避免数值不稳定性,需要满足稳定条件[式(6)]和网格离散条件[式(7)],即

(6)

(7)
式中:Δt、Δx分别为时间离散步长和空间离散步长;vmax、vmin分别为介质内的最大波速和最小波速;fN为奈奎斯特频率;G为由有限差分格式类型和阶数决定的常数,对于四阶交错网格有限差分,G=4。
2 混凝土主要组分材料声学参数测试
混凝土的宏观属性特征取决于内部组分材料的物理属性、含量和空间分布,因此超声波在混凝土中的传播规律与其在传播路径上所遇介质的声学特性和分布方式密切相关。为此,考虑骨料粒径的影响,选择两种粒径大小的碎石骨料用以浇筑混凝土,两组碎石骨料的岩性均为玄武岩,仅在粒径尺寸上有分别。其中大尺寸骨料的公称最大粒径为25 mm,小尺寸骨料的公称最大粒径为12.5 mm。另外,选择标号为42.5的硅酸盐水泥作为胶凝材料,当地河砂作为细骨料。
考虑水灰比和含砂率对水泥砂浆基质声学参数的影响,按照0.4和0.5两种水灰比,1∶1、1∶1.5和1∶2三种灰砂比,浇筑了6组水泥砂浆试样,每组包含3个试样。混凝土和水泥砂浆试样浇筑完成后,置于恒温恒湿养护箱中养护28 d。
为获得骨料的声学特性参数,选择与骨料相同岩性的玄武岩块用于制备岩样,水泥砂浆试样和玄武岩试样被加工成直径5 cm、长度10 cm的圆柱形。
对水泥砂浆材料和骨料岩样的密度、速度和纵波品质因子Q进行了测量,其中,速度和品质因子Q均采用分析脉冲透射波的方法进行测量,试验中使用的测量设备包括任意波形发生器(KEYSIGHT 33500B Series)、示波器(KEYSIGHT DSOX 1102G)和宽频带超声波探头(OLYMPUS V191),经过试验,示波器可以敏锐地捕捉到透射信号,因此没有在测量系统中接入功率放大器。设备连接示意图和超声波探头的照片如图2所示。
测量得到的水泥砂浆试样的速度如图3所示,可以看出超声波在水泥砂浆材料中的传播速度与砂的含量呈正相关关系,砂的含量越大,波速越高;超声波波速与水灰比呈负相关,灰砂比一定时,水灰比越大,波速越低。
计算得到的水泥砂浆试样相应的密度参数如图4所示,当水灰比为0.5时,水泥砂浆的密度随着含砂量的增多而增大;当水灰比为0.4时,灰砂比为1∶2的水泥砂浆密度要小于灰砂比为1∶1.5的密度。另外,测试玄武岩试样的平均速度为6 217 m/s,密度为2 760 kg/m3。

图2 测量设备Fig.2 The measuring equipment
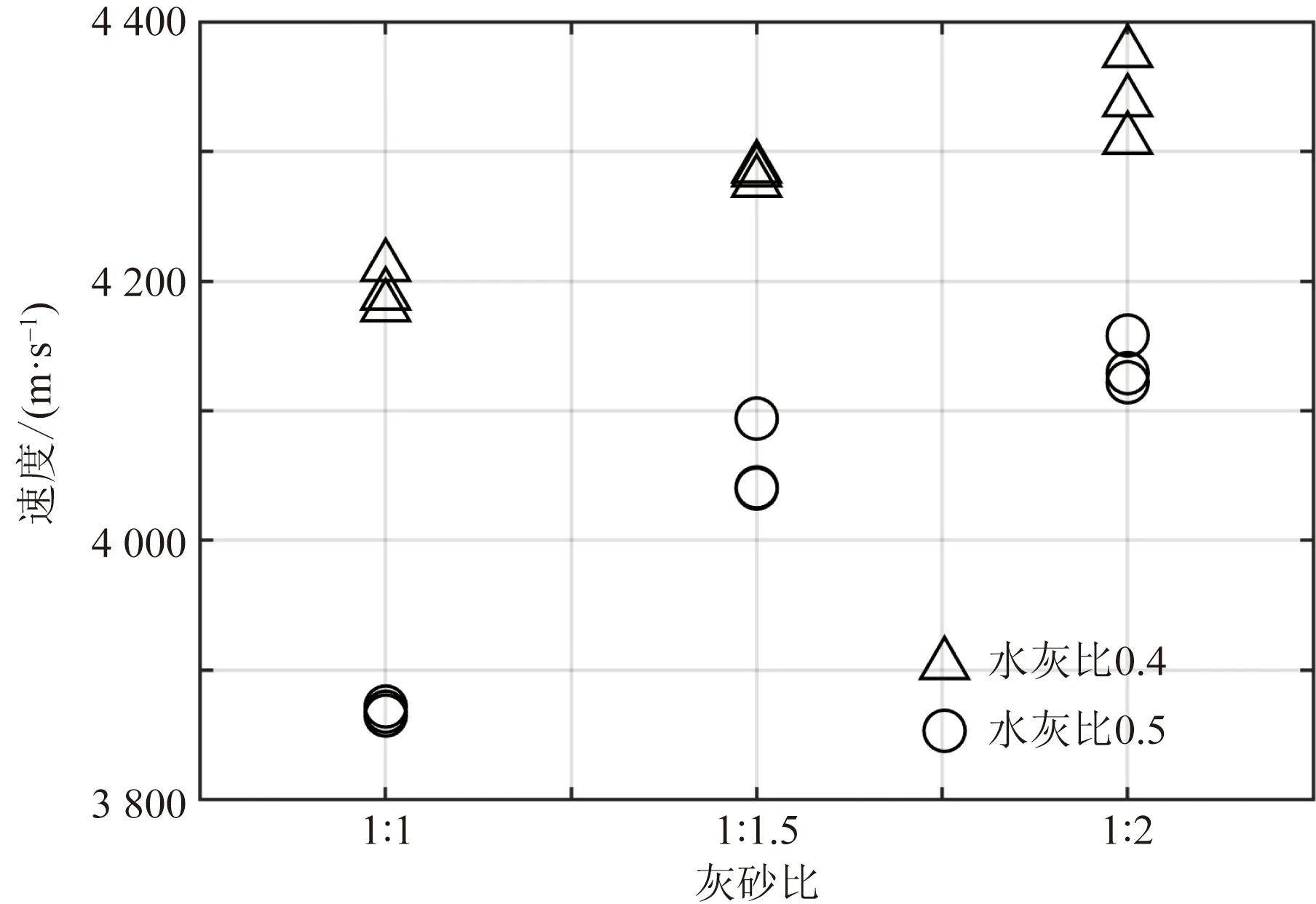
图3 不同配合比的水泥砂浆速度Fig.3 The velocity of cement mortar with different mix ratio

图4 不同配合比水泥砂浆的密度Fig.4 The density of cement mortar with different mix ratio
品质因子Q是表征介质固有衰减的一个重要物理量,在此采用谱比法测量计算水泥砂浆和骨料的品质因子Q。详细的描述可以在文献[17]中查阅。为了测量品质因子,通常需要准备与研究样品形状和尺寸相同的参考样品,这里选择直径为5 cm、高为10 cm的圆柱形铝作为参考样品。
在相同的条件下,用短脉冲宽频带信号对待测样本和金属铝样采用透射测量。铝样和待测样本的透射波振幅可以表示为
A1(f)=G1(x)e-α1(f)xei[2πft-k1(x)]
(8)
A2(f)=G2(x)e-α2(f)xei[2πft-k2(x)]
(9)
式中:A为振幅;f为频率;x为传播距离;k=2πf/v为波数,v为速度;G(x)为包括几何扩散、反射等的几何因子,下标1和2分别指铝样和待测样品;α(f)为与频率线性相关的衰减系数,其频率相关性可以表示为
α=γf
(10)
式(10)中:γ为与品质因子有关的常数,关系式为
(11)
将式(8)和式(9)的比值取对数可得

(12)
铝样和待测样品具有完全相同的形状和尺寸,因此G1和G2是与频率无关的标量,另外将金属铝视为完全弹性介质,其Q值接近无限大,即γ2=0,则待测样品的品质因子Q可由ln(A1/A2)与频率f拟合的直线的斜率求得。
按照上述方法,以某个水泥砂浆试样和玄武岩为例,阐述应用谱比法计算品质因子的具体步骤如图5所示。首先从记录信号中截取2个周期的直达波波形数据如图5(a)、图5(d)所示,然后对截取信号做傅里叶变换得到振幅谱如图5(b)、图5(e)所示,最后取铝样和待测样品振幅比值的对数为纵坐标,以频率为横坐标,做出拟合直线如图5(c)、图5(f)所示,并求出直线的斜率。按照上述计算品质因子的流程,对各个水泥砂浆试样和玄武岩的数据进行分析计算,水泥砂浆的品质因子如图6所示,水泥砂浆的品质因子取值主要在40~70范围内,水灰比和灰砂比对品质因子没有明显的影响规律。另外,玄武岩试样的平均品质因子为255。
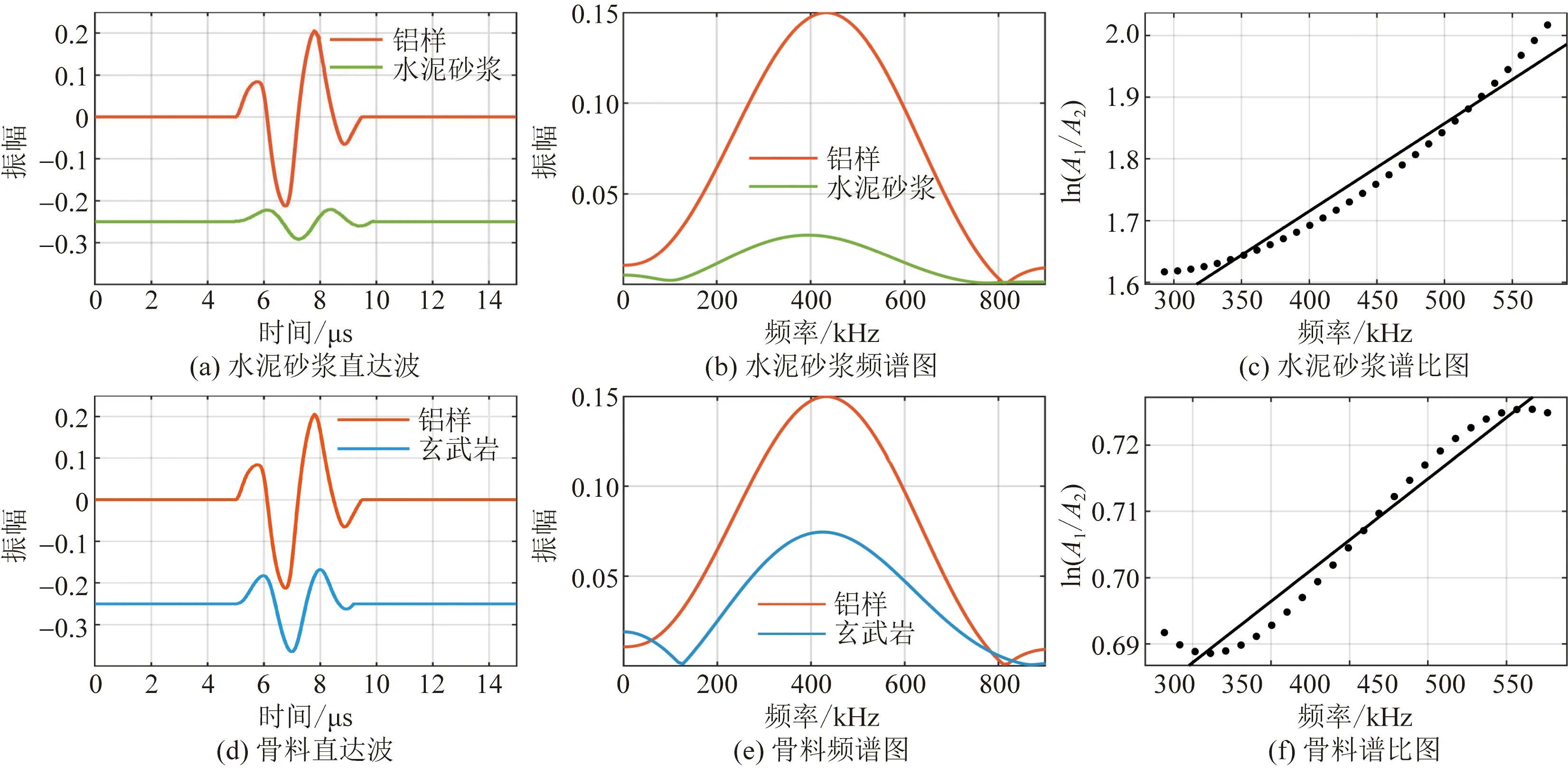
图5 待测样品品质因子计算过程图Fig.5 The calculation process diagram of quality factor of samples to be tested
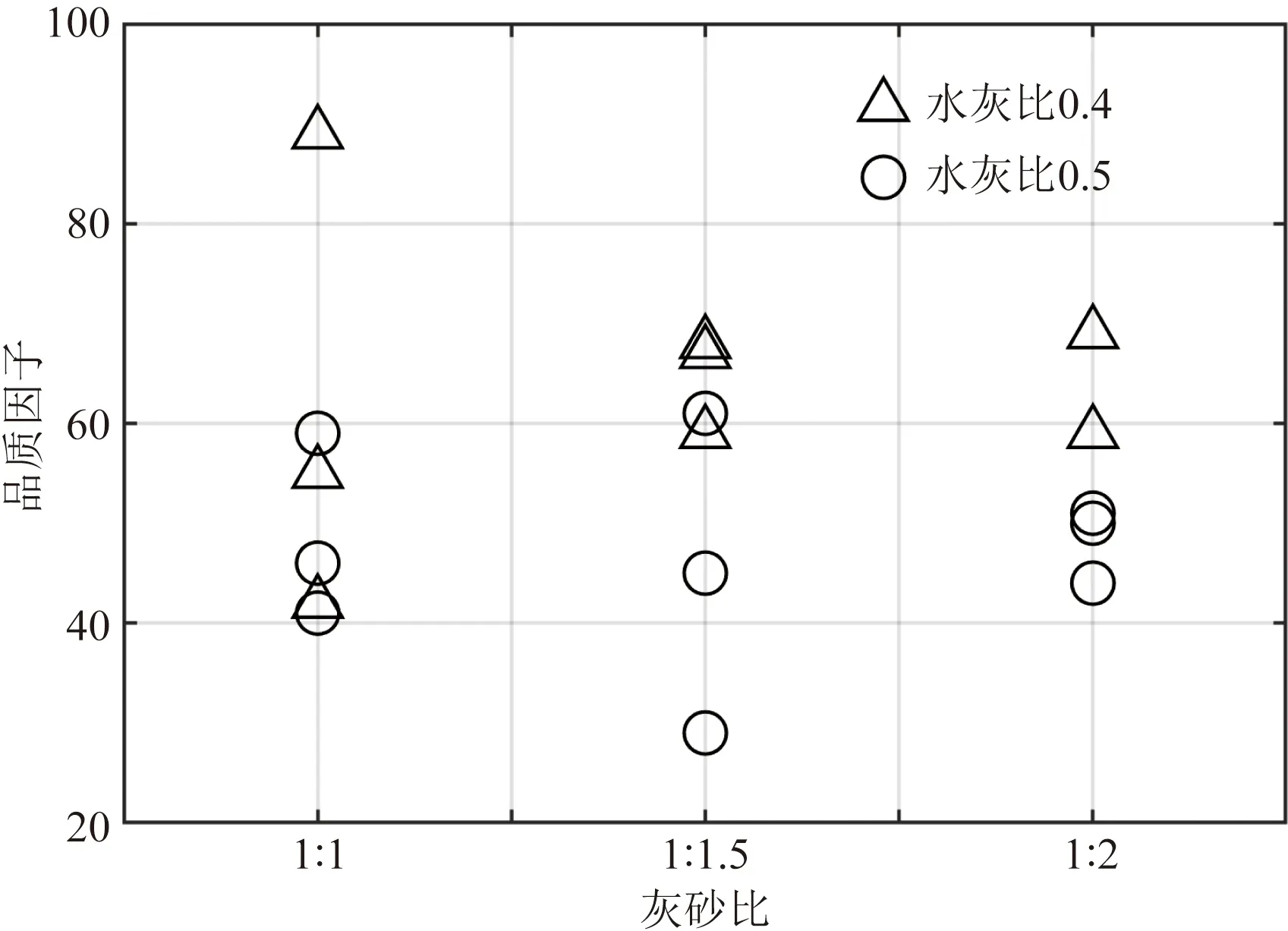
图6 水泥砂浆品质因子Fig.6 Quality factors of cement mortar
3 数值混凝土模型
混凝土作为一种作为典型的随机非均匀介质,其材料组成特别是骨料结构对超声波的能量扩散有着不利影响,在研究超声波的能量衰减时不能忽视这一点。为了考虑随机骨料结构的影响,在数值模拟中引入了数值混凝土。利用数字图像处理技术,对混凝土切片图像进行阈值分割处理,可以提取混凝土内部粗骨料的几何形体,从而建立精确的二维混凝土随机骨料模型。如图7所示为不同骨料结构的混凝土切片图像及其对应的随机骨料模型,其中图7(a)、图7(b)所包含的主要是大粒径骨料,为了方便叙述用A表示此类混凝土;图7(c)、图7(d)由小粒径骨料密集填充组成,用B表示此类混凝土;图7(e)、图7(f)由较少量的小粒径骨料填充而成,用C表示此类混凝土。
阈值分割后得到的混凝土随机骨料模型,可用于统计骨料的体积比和粒径分布特征。混凝土切片中骨料的体积比p可以表示为

图7 不同粒径骨料组成的混凝土及其对应的 数值混凝土模型Fig.7 Concrete with different size aggregates and its corresponding numerical concrete models
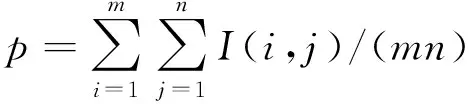
(13)
式(13)中:m、n分别为切片图像长、宽对应的像素点数。
按照式(13)计算得到图7中A类混凝土的体积比约为0.55,B类混凝土的体积比约为0.59,C类混凝土的体积比约为0.45。
为统计混凝土中骨料粒径的分布,依次计算切片中各个骨料的最小外接矩形,通过将最小外接矩形边长由像素单位转换为长度单位,来统计混凝土中骨料粒径的分布。单个骨料最小外接矩形的计算流程总结如下。
步骤1计算骨料的凸包多边形,并求凸包多边形各边与水平坐标轴的夹角θi。
步骤2根据凸包多边形上、下、左、右4个方向上的最远点,确定初始外接矩形,并计算矩形的周长和面积。
步骤3将凸包多边形按照角度θi旋转,使其一条边与坐标轴平行,再次根据旋转后凸包多边形上、下、左、右4个方向上的最远点,确定新的外接矩形,此时新外接矩形的至少一条边与凸包多边形的边重合,计算新矩形的周长和面积。
步骤4比较初始矩形和新矩形的周长和面积,按照周长或者面积最小原则,保留较小者作为初始矩形。
步骤5重复步骤3和步骤4,直到试算完所有的角度θi。
步骤6输出最小外接矩形。
如图8所示展示了单个骨料最小外接矩形的计算流程。
按照最小外接矩形方法,对模型内每个骨料的粒径进行测量,统计图7中3种数值混凝土模型的骨料粒径并绘于图9,可以看出,A类模型最大骨料粒径约为37.5 mm,B、C模型的曲线差别主要是由4.75 mm以下的骨料数量差异所致,4.75 mm粒径以上的骨料分布较为一致,两者最大骨料粒径约为19.34 mm。
4 混凝土中超声波的衰减特征
由于混凝土的随机非均匀性,在超声波传播路径上遇到波阻抗不连续界面会发生反射、散射等现象,造成波前能量耗散。研究混凝土内骨料含量、骨料粒径、水灰比、含沙量等随机参量对超声波能量和频率衰减的影响,可以为选择最佳超声波检测参数(频率、激励电压等)和检测结果的解释提供依据。基于黏弹性声波方程,模拟超声波在图7所示3类数值混凝土模型中传播,为保证结果的可靠性,每类数值混凝土选择3个样本。
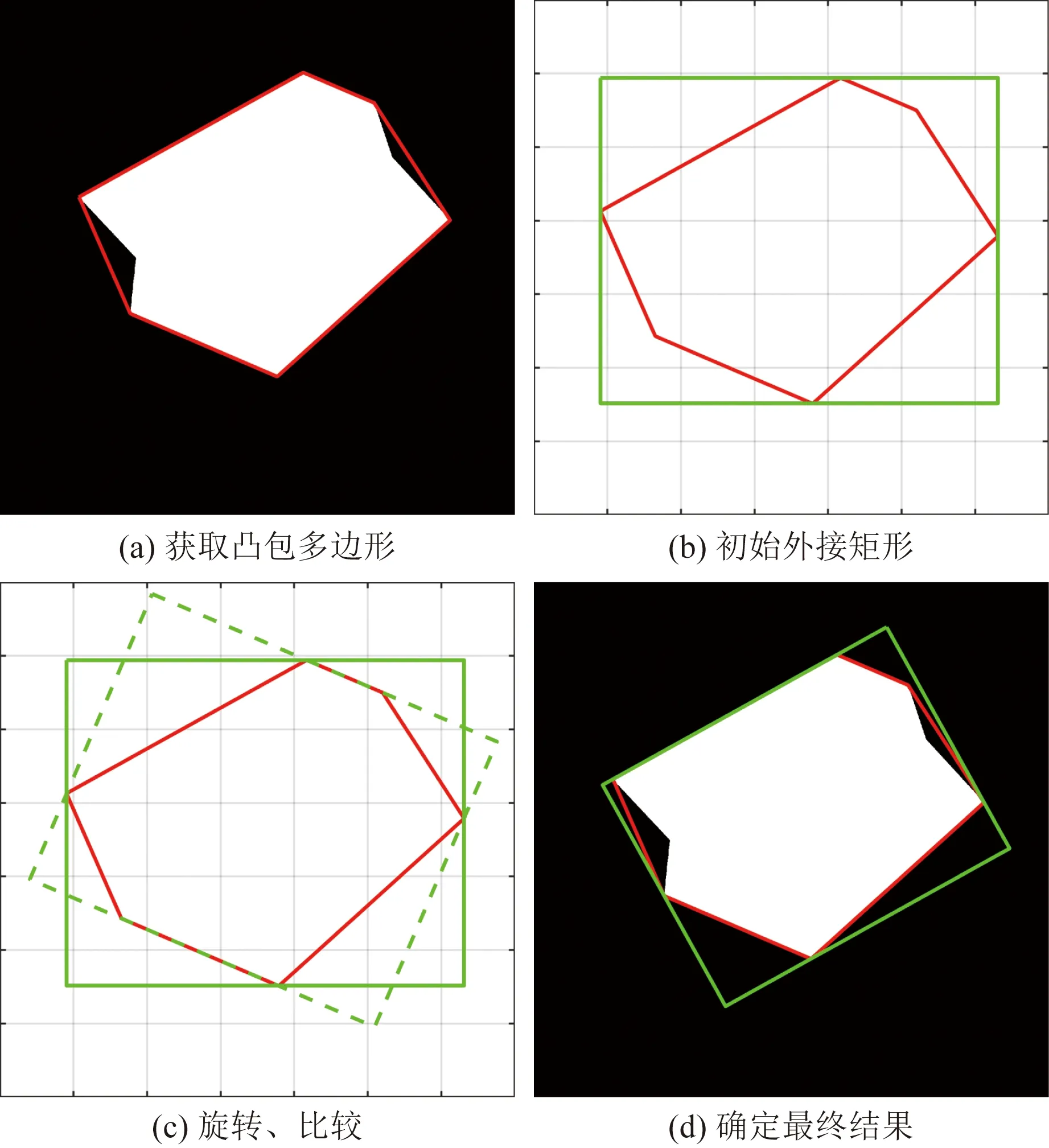
图8 骨料最小外接矩形计算流程Fig.8 Calculation flow of minimum enclosing rectangle of aggregate

图9 随机骨料模型的骨料粒径分布曲线Fig.9 The aggregate gradation distribution curves of random aggregate model
得到20 μs时刻的波场快照如图10所示,可以看出,受混凝土非均匀性的影响,波场内存在大量散射波,波前信号间断不完整、能量微弱,这种现象在A类混凝土中尤为明显。
超声波在混凝土中的衰减计算公式为
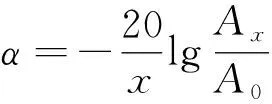
(14)
式(14)中:x为超声波传播的距离;Ax为超声波传至x位置的幅值;A0为超声波的初始振幅值。另外,这里的振幅是指波前信号的振幅。

图10 200 kHz超声波在3种数值混凝土中 20 μs时刻的波场快照Fig.10 Snapshot of wave field of 200 kHz ultrasonic wave at 20 μs in three kinds of numerical concrete
4.1 骨料粒径对超声波衰减的影响
考虑混凝土骨料粒径的影响,在数值模拟中选择骨料含量接近,而骨料粒径分布不同的A、B两种混凝土,两者细观材料声学参数相同如表1所示。
得到的不同频率超声波的透射波形如图11所示。可以看出:当入射波频率为50 kHz时,接收到的透射波的形状与入射波基本一致,A(大粒径骨料)和B(小粒径骨料)两种混凝土的透射波在幅值大小上没有明显的区别。随着频率的升高,骨料的影响逐渐显著,在直达波之后伴随着不规则的杂波,这是超声波在骨料表面发生反射和散射所致,超声波的频率越高,杂波越多,透射波的幅值也越小,A类混凝土中的透射波幅值要小于B类混凝土。

表1 含不同粒径骨料的数值混凝土模型Table 1 The numerical concrete models with different size aggregates
为了定量描述超声波能量和频率的衰减程度,从图11信号中截取出直达波的波形数据,这里选取入射波和透射波从初至时间开始经两个周期的波形作为直达波波形数据,计算入射波和透射波的振幅谱,根据式(14)绘制超声波随入射波中心频率变化的能量衰减曲线和透射波峰值频率变化曲线如图12所示,其中图12(b)中的百分比数字表示相较于入射波的衰减百分比。
从图12可以发现:经过混凝土后,透射波的峰值频率会向低频区域偏移,并且频率越高,这种偏移程度越大;入射波的峰值频率越高,得到的透射波的振幅值衰减越大,由于混凝土的随机性,即使同种类型的混凝土模型之间在峰值频率和最大振幅值上也存在一定的差别;A类混凝土(大粒径骨料)的衰减作用要强于B类混凝土(小粒径骨料)。
4.2 骨料含量对超声波衰减的影响
为了研究骨料含量对超声波传播的影响,对比了不同频率超声波在B类和C类混凝土中的能量和频率衰减特征,其中,包含C类随机骨料模型的数值混凝土的设置如所表2示,模型3除随机骨料模型与表1中模型2不同外,两者的其他属性参数均一致。
为了比较超声波在不同骨料含量的混凝土中的传播特征,将表1中模型2和表2中模型3的能量和频率衰减曲线绘制在一起,如图13所示。

图11 超声波在不同粒径骨料组成的混凝土中的时域波形图Fig.11 Time domain waveforms of ultrasonic wave in concrete composed of aggregate with different sizes

图12 不同粒径骨料混凝土中超声波的能量 衰减和峰值频率变化曲线Fig.12 The curves of ultrasonic energy attenuation and peak frequency variation in concretes with different sizes aggregates

表2 低骨料含量的数值混凝土模型Table 2 The numerical concrete model with low aggregate content
结果显示,对于相同频率条件下,低骨料含量混凝土中超声波的能量和频率衰减更大,这与以往的研究不同。在混凝土中,骨料一般被认为是嵌入水泥砂浆基质中的非均质体,是造成超声散射的主要散射体,因此,认为骨料越多,散射作用越强烈,造成的衰减越大。但本质上是超声波在介质内部传播过程中,遇到波阻抗不连续界面发生反射和散射,从而造成能量的耗散。混凝土内部的波阻抗分界面,主要是骨料和水泥砂浆材料的分界面,当骨料的含量较高时,混凝土内部的骨料密集堆积分布,水泥砂浆填充骨料之间的空隙,这种情况下超声波更多的在骨料中传播,并且空隙的尺寸要小于骨料,因此对超声波的散射衰减作用要弱于低骨料含量的混凝土。结合文献[17]的研究成果认为,当骨料的体积占比小于0.5时,超声波的能量衰减随着骨料含量的增加而增大;当骨料的体积占比大于0.5时,超声波的能量衰减随着骨料含量的增加而减小。
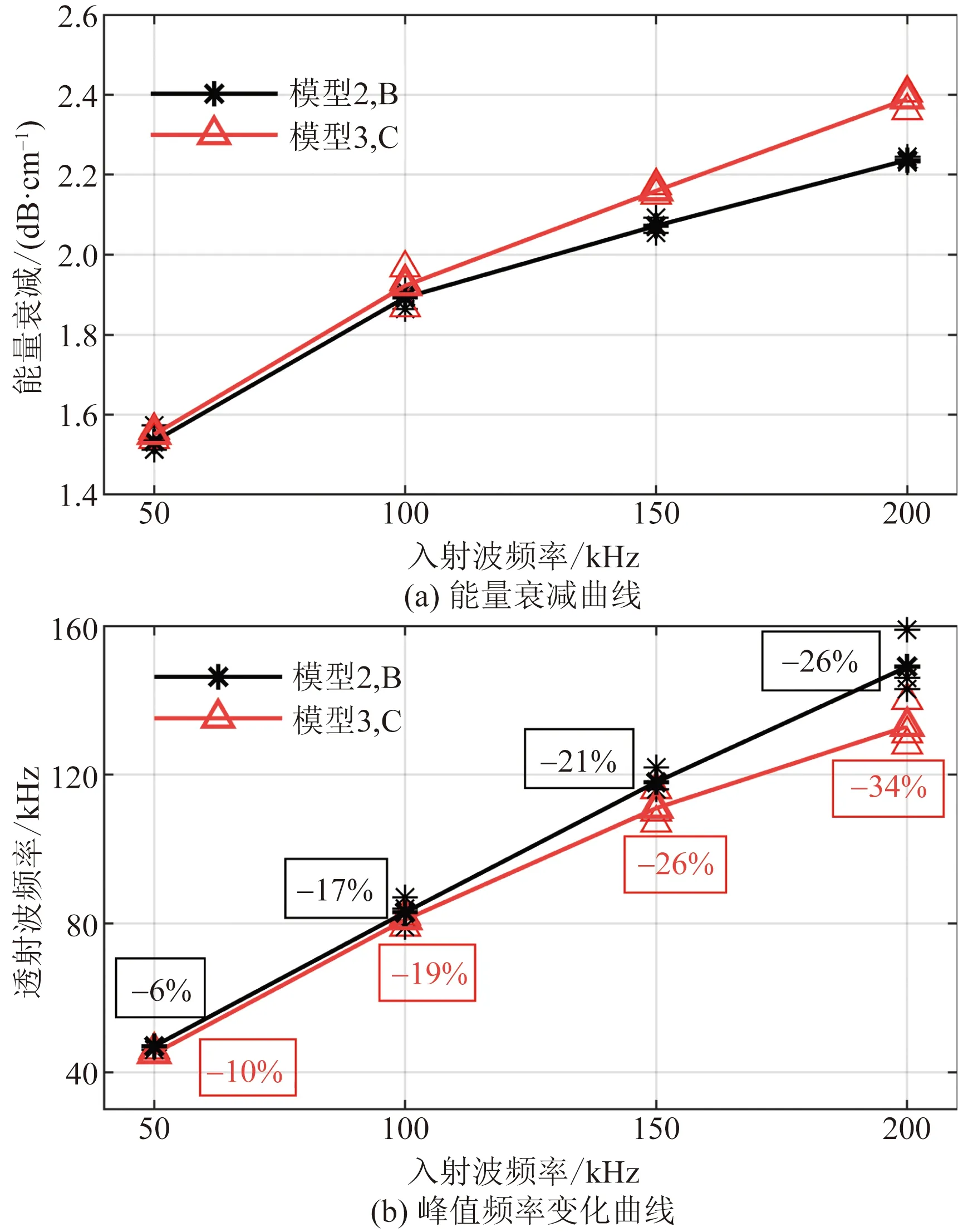
图13 不同骨料含量混凝土中超声波的 能量衰减和峰值频率变化曲线Fig.13 The curves of ultrasonic energy attenuation and peak frequency variation in concretes with different aggregates content
4.3 水泥砂浆速度对超声波衰减的影响
为了研究水泥砂浆速度对超声波传播的影响,另设置声波的速度为3 800 m/s的模型,具体参数设置如表3所示。
绘制超声波的能量衰减曲线和透射波的峰值频率变化曲线如图14所示,相比于模型3,模型4有着更高的能量衰减和频率衰减。在研究中发现,骨料的声阻抗越大,超声波的能量衰减越大[8]。与之对照可以得出结论,水泥砂浆和骨料的声阻抗参数差异越大,超声波的能量衰减和频率衰减越大。

表3 数值混凝土的参数设置(3 800 m/s)Table 3 The acoustic parameters of numerical concrete(3 800 m/s)
4.4 水泥砂浆品质因子对超声波衰减的影响
为了研究水泥砂浆的品质因子对超声波传播的影响,另设置水泥砂浆的品质因子Q=90的模型,具体参数设置如表4所示。绘制超声波的能量衰减曲线和透射波的峰值频率变化曲线如图15所示,相比于模型3,模型5的能量衰减要小一些,并且这种差别基本不随频率的变化而改变。

图14 不同水泥砂浆速度下超声波的能量衰减和 峰值频率变化曲线Fig.14 Curves of ultrasonic energy attenuation and peak frequency variation with different cement mortar velocities

表4 数值混凝土的参数设置(Q=90)Table 4 The acoustic parameters of numerical concrete(Q=90)
5 结论
超声波传播参数对混凝土结构损伤与性能退化异常敏感,可是作为典型的随机介质,混凝土的随机非均匀性对超声波的传播有着复杂的影响,骨料的尺寸和含量影响超声波能量的散射衰减,不同配合比的水泥砂浆影响超声波在其中的传播波速和固有吸收衰减,而不同频率的超声波因波长的不同,所受影响程度又有不同。为深入揭示混凝土自身随机非均匀性对超声波传播的影响,本文围绕混凝土细观组分随机非均匀性对超声波衰减特征的影响展开研究,利用数字图像处理技术从混凝土截面图像中提取真实的骨料结构,引入Kelvin-Voig黏弹性模型用以表征材料的固有吸收作用,基于有限差分算法模拟了超声波在混凝土中的传播,定量计算了超声波传播特征,探讨了骨料粒径、骨料含量、水泥砂浆速度和品质因子对超声波衰减的影响规律,主要得到以下结论。

图15 不同品质因子混凝土中超声波的能量衰减和 峰值频率变化特征Fig.15 The energy attenuation and peak frequency variation characteristics of ultrasonic wave in concretes with different quality factor
(1)混凝土骨料粒径是影响超声波衰减的重要因素,骨料粒径越大超声波在传播过程中能量衰减越大,同时中心频率向低频方向偏移程度越大。
(2)骨料含量是影响超声波能量衰减的另一因素,当骨料的体积比小于0.5时,超声波的能量衰减随骨料含量的增加而增大;当骨料的体积比大于0.5时,超声波的能量衰减随骨料含量的增加而减小。
(3)骨料和水泥砂浆的声阻抗差异是导致超声波发生散射现象的原因,通常水泥砂浆材料中波速要小于碎石骨料的波速,因此水泥砂浆波速越大,超声波在混凝土中传播时的衰减越小;反之,则衰减越大。
(4)骨料的散射作用对骨料粒径、骨料含量和材料的声阻抗属性敏感,并且频率越高,散射作用越强烈,而固有吸收作用仅与品质因子有关,随频率变化不大;随着频率的升高,散射衰减随之明显增大,散射衰减可以视为主要的衰减机制。
(5)利用超声波对混凝土进行检测时,建议入射频率范围为50~100 kHz。

