基于GA-BP神经网络的机器人抛光曲面粗糙度预测①

段鹏飞

(安徽工程大学机械工程学院，安徽 芜湖 241000)

0 引 言

随着社会的发展，在现代机械制造中，工业机器人抛光加工成为一种重要技术，对机械发展起着重要作用[1〗。已有的抛光技术虽可以完成产品加工，但无法提前预知产品抛光的表面粗糙度值，这无疑制约了对产品的智能化生产加工，且容易造成资源的浪费。因此，对需要加工的产品结合神经网络进行粗糙度预测，有很重要的研究意义[2-5]。

文献[6]用铝合金板材进行机器人砂带磨削实验，用磨削数据对网络进行训练，得到砂带磨削粗糙度与磨削参数的预测模型，验证了模型预测的相对准确性；文献[7]对于无法精确预测铣削零件表面粗糙度的问题，把铣削实验数据分成训练和测试两种，用铣削实验数据对网络进行训练，得到零件粗糙度与铣削参数的预测关系。现有的针对机器人抛光粗糙度预测研究多是通过工件实验数据来对BP神经网络进行训练，通过训练最终得到粗糙度预测模型[8]。BP神经网络权值和阈值是随机选取的，且神经网络不是对多个数据同时进行搜索，可能会得到局部极小值，从而无法表征全局[9]。因此，BP算法存在学习速度慢，不易收敛，可能进入局部最优解，造成预测误差较大等缺点[10]。

基于遗传算法优化BP神经网络来预测机器人抛光曲面的表面粗糙度，用遗传算法对神经网络初始权值和阈值进行优化，建立了以抛光工具粒度、转速、压缩量和进给速度为神经网络输入的抛光曲面粗糙度预测模型。

1 抛光曲面粗糙度预测模型建立

1.1 BP神经网络原理

神经网络以机器人抛光工具的粒度、转速、压缩量和进给速度作为输入层，粗糙度值作为输出层，建立机器人抛光曲面粗糙度预测模型。BP神经网络对于复杂的非线性关系有很强的归纳预测能力，全局搜索，泛化能力强。BP网络的理论学习过程如下：

设网络输入层节点为I=(i1,i2，…,ia)，隐含层节点为H=(h1,h2,…,hb)，输出层节点为O=(o1,o2,…,oc)，输出层期望向量为Y=(y1,y2,…,yc)，隐含层的阈值向量为G=(g1,g2,…,gb)，输出层阈值向量为L=(l1,l2,…,la)，输入层与隐含层之间的网络权值为Vsj，隐含层与输出层之间的网络权值为Vjk，其中，s=1,2,…,a；j=1,2,…,b；k=1,2,…,c。

则隐含层节点输出为

(1)

netj=VsjIs-gj

其中，f为激活函数。

输出层输出为

(2)

netk=Vjkhj-lk

输出层误差函数为：

(3)

基于误差函数对输出层各节点求偏导可得

(4)

基于输出层的Wk与隐含层的误差函数，对隐含层各节点求偏导可得

(5)

基于输出层的Wk与隐含层的Zj，对权值Vsj和Vjk进行修正，其最终的总误差计算表达式为

(6)

BP神经网络把学习误差和目标精度作比较，确定是否进行下一次学习，当误差达到目标精度时则停止学习。遗传算法经过选择得到新的个体，从中选择适应强的染色体，通过交叉变异得到更新的权值和阈值，从而得到全局最优解。

1.2 GA-BP算法的实现

提出的遗传算法优化BP神经网络由三部分组成，首先通过机器人抛光曲面的参数来确定神经网络拓扑结构；然后通过遗传算法中的交叉变异对个体进行选择，选出优化后的个体；最后对选出的个体进行解码得到各自的参数，用数据对BP神经网络进行训练，从而得到预测模型。

机器人抛光曲面粗糙度预测模型中，将机器人抛光曲面实验中的抛光工具粒度、转速、压缩量和进给速度等参数测得的数据作为样本进行训练，用抛光曲面粗糙度值进行测试，然后进行归一化处理，建立预测模型，遗传算法优化BP神经网络实现流程如下：

(1)把机器人抛光曲面粗糙度预测中，机器人抛光工具粒度、转速、压缩量和进给速度等参数测得的数据作为训练样本，归一化处理实验数据。

(2)设置遗传算法参数，对BP神经网络训练次数，训练精度等参数进行设置。

(3)把机器人抛光曲面粗糙度预测中遗传算法的种群数目进行实数编码，并对种群进行初始化处理。

(4)用适应度函数筛选个体，对个体降序排列，解码得到个体的初始权值和阈值。

(5)对降序排列的个体进行选择，对个体进行交叉变异操作。

(6)把机器人抛光曲面粗糙度预测中，把实测值与预测值相比较，来判断个体是否达到最优，达到最优则输出，反之则循环上述步骤。

(7)把得到的最优个体解码操作，得到机器人抛光曲面粗糙度预测模型的最优参数。通过这些参数对BP网络进行训练，最终得到相对准确的预测结果。

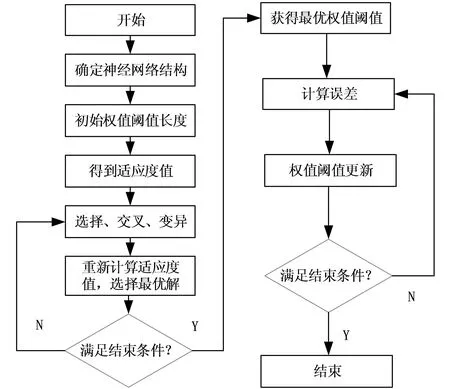
图1 GA-BP预测流程图

1.3 建立抛光曲面粗糙度预测模型

在机器人抛光曲面粗糙度预测模型中，抛光工具的粒度、转速、压缩量和进给速度对粗糙度的影响最大，因此神经网络的输入层选择这4个因素，输出层为粗糙度值，隐含层选择5层。机器人抛光曲面粗糙度预测中，遗传算法优化BP神经网络模型如图2所示。

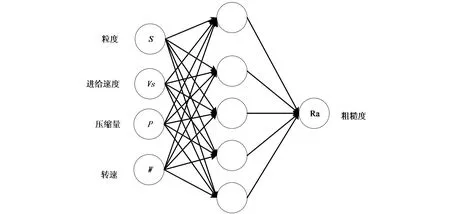
图2 GA-BP神经网络模型

机器人抛光曲面粗糙度预测中，用newff函数构建BP神经网络，初始化种群，解码得到初始权值和阈值。设置遗传算法参数，个体交叉概率为0.1，变异概率为0.1，进化代数为50代，种群规模为150。用code函数将变量进行编码来初始化种群，阈值和权值是否超出范围用test函数来判定，然后用fun函数计算种群适应度，得到种群的初始化信息。Select函数进行选择，通过交叉变异得到最优个体。把得到的最优个体解码操作，得到机器人抛光曲面粗糙度预测模型的最优参数。通过这些参数数据对BP网络进行训练，最终得到相对准确的预测结果。

2 预测结果及分析

用遗传算法优化BP神经网络对机器人抛光曲面前20组数据进行训练，经过全局搜索以及交叉、变异，筛选出最优个体，对神经网络进行优化后，用后9组数据进行仿真，得到BP网络预测适应度曲线如图3所示。

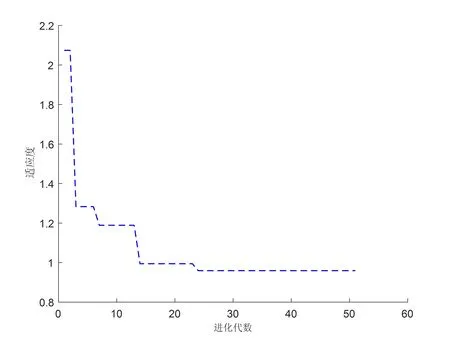
图3 适应度曲线图

通过对数据不断训练、仿真，得到BP神经网络和遗传算法优化后机器人抛光曲面粗糙度预测的误差对比，如表2所示。可以看出单一BP神经网络预测容易产生极小值现象，预测误差相差较大，这是BP算法的限制造成的，使得预测精度低，数据难以收敛。遗传算法对全局进行搜索，经过交叉变异，筛选出最优个体，解码处理得到最优参数，用得到的数据对BP神经网络进行训练，与单一BP神经网络预测相比，相对误差较小，能够得到相对精确的机器人抛光曲面粗糙度预测模型。

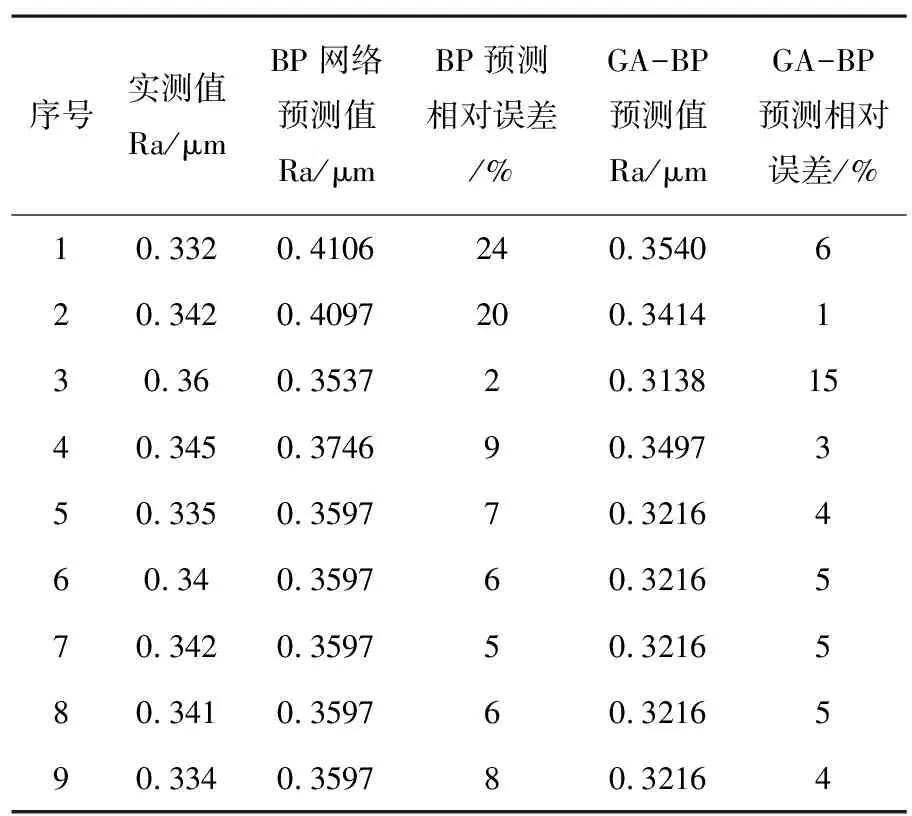
表1 预测误差对比

经遗传算法优化后的机器人抛光曲面粗糙度预测误差和误差百分比，如图4和图5所示。

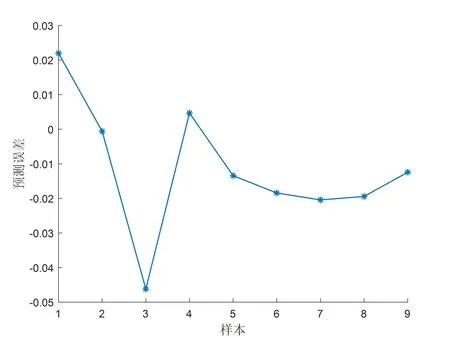
图4 BP网络预测误差

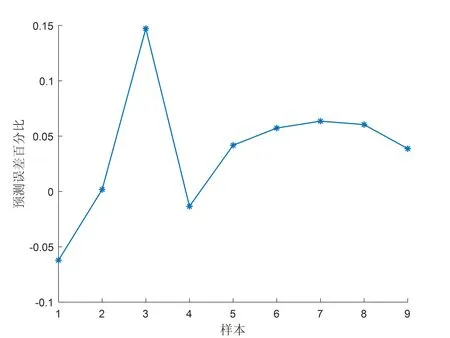
图5 预测误差百分比

改进后的BP网络抛光曲面粗糙度预测的最大误差值为0.046，预测的最小误差值为0.0006。改进后的BP网络预测误差百分比最大相对预测误差为15%，最小相对预测误差为1%。与单一的BP神经网络预测模型相比，通过遗传算法优化BP神经网络的机器人抛光曲面粗糙度预测模型稳定性好，具有很好的收敛性，无极小值现象，且预测精确度较高。

把遗传算法优化后和未优化的神经网络的预测数据与实测数据相比较，绘制出数据对比图，如图6所示。

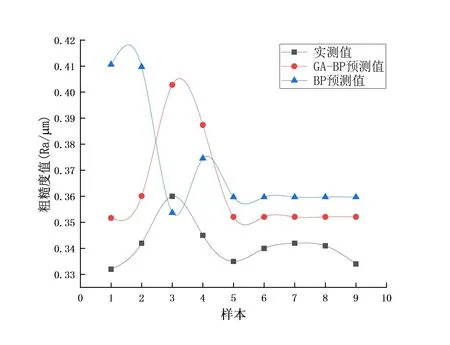
图6 数据对比图

可以看出，遗传算法优化后的预测曲线和实测值曲线保持一致性，而未优化的数据曲线波动较大，无法与实测曲线保持一致，说明经遗传算法优化后预测结果较为准确，预测稳定性好。

3 结 语

通过遗传算法优化BP神经网络，建立了机器人抛光曲面粗糙度预测模型。解决了单一BP神经网络预测误差较大，收敛性差，难以得到全局最优解的问题。机器人抛光曲面粗糙度预测模型预测误差小，且预测较稳定，可以更好的对机器人抛光曲面的粗糙度进行预测。该机器人抛光曲面预测模型和单一的BP神经网络预测相比预测更加准确，更适用于工程实践，对机器人抛光曲面粗糙度的预测具有较高的应用价值。