110 kV变电站钢框架结构的抗火性能
汪 洋,李 攀,顾 瑜,张 凯
(1.苏州电力设计研究院有限公司,江苏 苏州 215000; 2.同济大学土木学院地下建筑与工程系,上海 200092)
钢结构具有强度高、塑性韧性好、易连接、机械化程度高、抗震性能好等优点,被广泛应用于各类建筑中。如美国纽约的帝国大厦和旧金山的金门大桥,法国巴黎的埃菲尔铁塔,以及中国北京的国家鸟巢体育场、首都国际机场航站楼和新央视大楼等都采用了大量的钢结构。然而,钢结构的一个非常显著的缺点是抗火性能差。在实际情况,钢结构在发生火灾时往往只有十几分钟的支撑能力,之后建筑结构将会迅速倒塌[1]。
结构抗火问题是一个非常复杂的综合性问题,影响钢结构抗火性能的因素众多。国内外抗火理论研究,主要包括火灾下室内温度场的研究、高温下建筑结构钢材物理性能和力学性能的研究,以及结构抗火性能设计与计算等。文献[2]提出了的火灾在全盛升温过程中的温度计算模型。欧洲规范EUROCODE[3]和美国土木工程师协会ASCE[4]分别给出了不同类型的火灾下建筑结构空间的升温计算模型。不同的经验模型描述火灾升温过程虽有些差异,但整体变化趋势一致。国外大多数建筑防火规范都采用解析法计算钢构件表面的温度,我国《建筑钢结构防火技术规范》同样采用解析法进行计算。在数值分析方法研究钢构件升温数值解时,多采用有限差分法和有限元法,有限差分法在应用上有些局限,有限元计算方法则有更好的适用性和通用性[5]。文献[6]通过不同钢材的拉伸试验,给出了高温下钢材强度的折减系数。Renner研究了S275钢的拉伸性能,指出钢材高温下的抗拉强度与应变速率相关。文献[7]在试验分析的基础上,给出了高温下钢筋的强度拟合公式。文献[8]对16Mn钢、SM41钢及S355钢等进行了大量的火灾高温试验,得出高温下钢材弹性模量的计算公式。
钢结构的抗火研究主要有两种方法,一种是采用同比例缩小尺寸的梁、柱或节点构件的试验方法;另一种是根据构件或结构的实际承载和约束工况,应用有限元理论,采用商用有限元软件进行等效模拟。两种研究方法各有利弊:①试验研究方法得到的结论只能适用于特定形式和工况下的结构设计,不具有普遍适用性,并且试验环境与实际应用环境的偶然影响因素较为复杂,不能保证试验工况能够有效模拟,但是试验研究具有易于操作和学习的优点;②有限元计算模拟方法适用于绝大部分的钢结构抗火设计研究,无论研究的对象是构件亦或是结构整体,通过分析构件或结构实际工况下的荷载及约束情况,定义使用材料的性能和边界条件,就可以有效模拟分析结构的性能。
建筑结构抗火,尤其是抗火性能较差的钢结构,是一个特别需要关注的问题。变电站结构,关乎一个地区或城市的用电安全,影响区域经济健康发展和社会稳定和谐。因此,变电站钢结构的抗火性能更需要深入研究,首先研究钢结构抗火的材料参数、火源模式等;然后采用热结构耦合方式研究不同工况下的温度场、结构变形、力学性能,并对耐火极限进行分析。
1 研究背景
以现行推广的装配式智能化变电站110 kV-A2-6方案为背景,开展变电站钢框架的抗火计算分析。“装配式变电站”,是指建筑钢构件在工厂预制完成后运输到工地,利用施工机械装配而成的变电站结构。钢结构建筑的抗震能力和预装性能都很突出,已被公认为是未来建筑的发展方向。在变电站领域,钢结构应用仍处于起步阶段,在全国范围内钢结构变电站仅有少量应用实例。装配式变电站使得变电站建筑物建设模式由传统“钢筋混凝土框架+砌体填充墙+现浇钢筋混凝土屋面”现场建造模式,转变为“钢框架+成品墙板+压型钢板底模混凝土屋面”的工厂制造模式。装配式建设常用的钢结构主体结构及墙板构件的耐火极限不如传统钢筋混凝土及砌体填充墙的,因此需要研究变电站钢结构的抗火性能,可为变电站抗火防护处理提供参考[9]。
本研究(装配式智能化变电站110 kV-A2-6方案)变电站钢框架整体结构如图1所示,是一个两层十榀的大型钢框架结构。钢框架一层高度4.5 m,二层高度8.0 m,每榀跨度从左至右分别为6,7.5,6,7.5,6,7.5,6,5,5 m,钢架最大跨度19 m。结构柱采用宽翼缘H型钢,框架主梁采用中翼缘H型钢,次梁采用窄翼缘H型钢,具体的材料尺寸及钢材等级见表1。
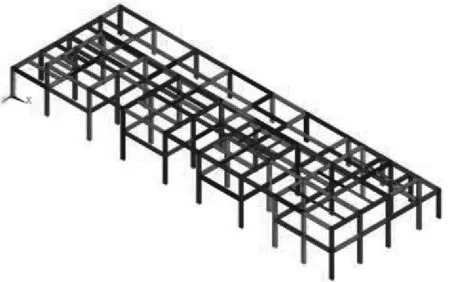
图1 变电站钢框架整体结构
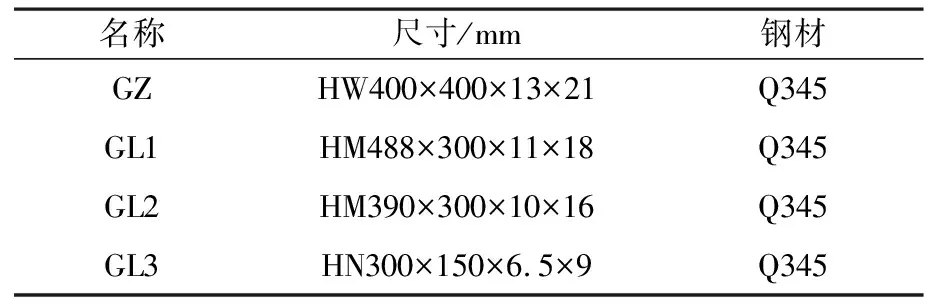
表1 钢结构材料表
2 热结构耦合方法
采用大型通用有限元软件ANSYS,采用热结构耦合方法研究钢结构的抗火性能。ANSYS软件不仅能解决纯粹的热分析问题,还能解决与热有关的其他诸多问题,如热-应力、热-电等。将这类涉及两个或两个以上的物理场之间的相互作用称为耦合场。耦合场分析的过程依赖于所耦合的物理场,可分为直接耦合和顺序耦合(间接耦合)两大类。当进行直接耦合时,多个物理场(如热-电)的自由度同时进行计算,适用于多个物理场各自的响应互相依赖的情况。间接耦合分析是以特定的顺序求解单个物理场的模型,将前一个分析的结果作为后续分析的边界条件。如在热应力分析中,用户可以先对结构进行热分析,然后将热分析所得到的节点温度作为“体载荷”施加到结构的节点上,求解后就可以得到由于温度分布不匀在结构上所产生的热应力[10]。本文使用间接耦合方法进行建模计算,具体的建模思路如图2 所示。

图2 ANSYS热-结构耦合计算思路
2.1 材料参数选取
钢结构抗火计算相关性能主要有二个方面:一是高温下钢材的热物理特性,主要用于钢结构(构件)内温度场的计算,具体包括高温下钢材的导热系数、比热容、密度等;二是高温下钢材的力学性能,主要用于高温下钢结构的内力计算、承载力验算以及变形计算,具体包括钢材的热膨胀性能、强度、弹性模量、应力-应变本构关系及松弛与蠕变效应等[11]。参数选择参考了相关规范,具体取值见图3~7(未考虑钢材的蠕变效应)。
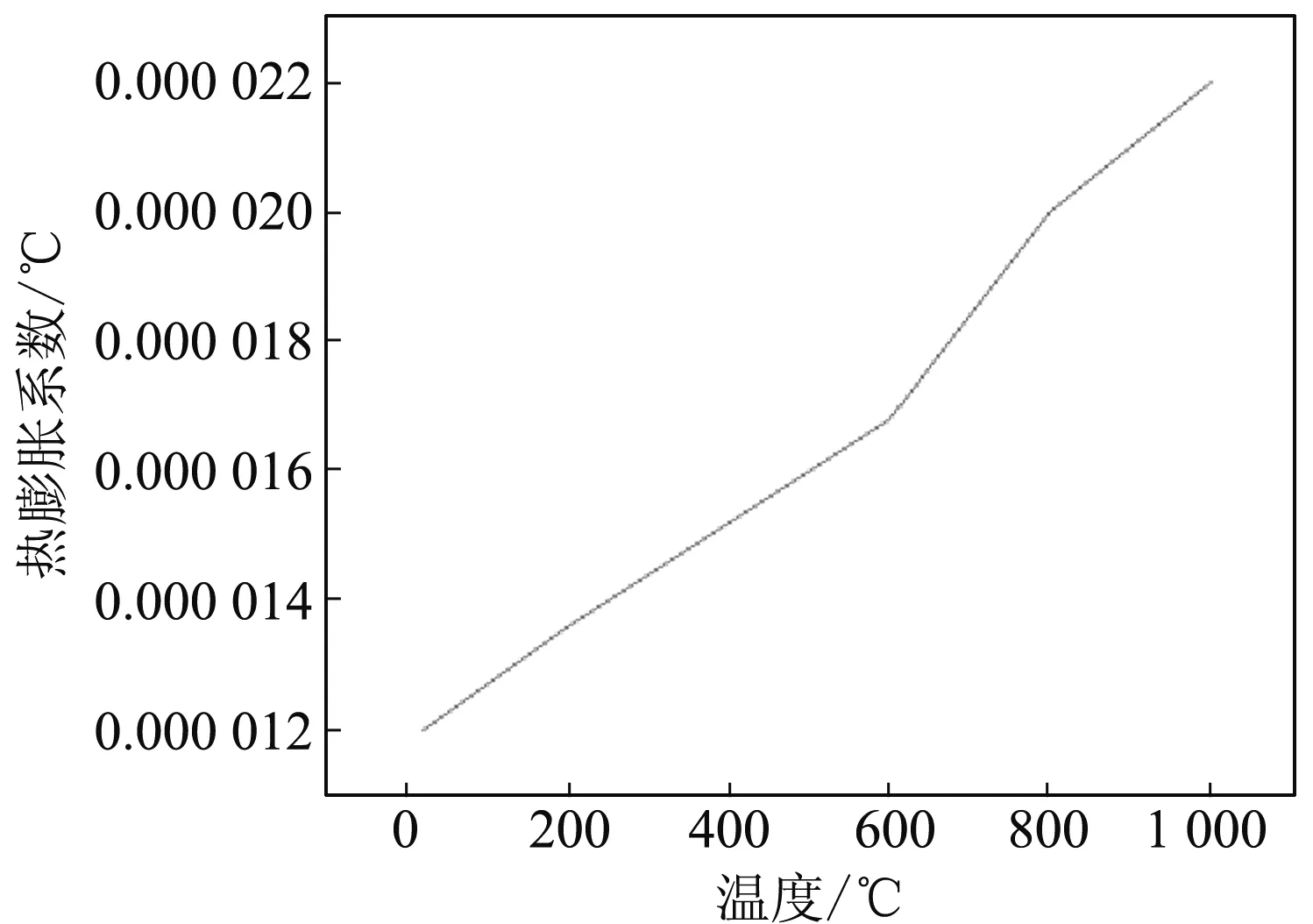
图3 热膨胀系数随温度的变化

图4 热传导系数随温度的变化

图5 比热容随温度的变化

图6 弹性模量随温度的变化

图7 应力-应变曲线随温度的变化
2.2 结构模型
本研究选取整体钢框架最右侧一榀平面结构为一个2层4跨连续钢框架,一层高4.5 m,二层高8 m,柱间距从左至右分别为5,5,5.5,3.5 m。梁柱尺寸如前述,具体尺寸如表2所示。

表2 模型尺寸
防火间具有防止火灾蔓延和隔绝热量传递的作用,仅防火间内部的结构件会有明显的温度上升。为了能准确模拟截面的非均匀温度分布和捕捉局部屈曲等现象,构成防火间的梁和柱将采用SOLID70单元用于传热分析,采用与SOLID70单元相对应的SOLID45单元用于结构分析。模型最终节点数53 515,单元数154 811。钢框架模型及局部网格划分情况如图8~9所示。

图8 钢框架整体结构模型
边界及荷载的施加情况如图10所示。所有柱脚固定;所有横梁都受均布荷载作用,荷载值为25 kN·m-1;柱顶受集中荷载作用,其中边柱受集中荷载作用,荷载值为75.5 kN,中间柱受集中荷载作用,荷载值为151 kN。

图9 结构梁柱节点模型

图10 荷载及约束情况
2.3 火源模式
(1)标准升温曲线。ISO 834《国际建筑材料耐火性能测定》给出的火灾标准升温模型如图11所示。

图11
该模型规定火定室内温度与时间的关系如下:
T=T0+345lg(8t+1)
(1)
式中T——温度,℃;T0——初始温度,℃;t——时间,s。
(2) 受火位置。研究4种方式的火灾模式,分别为一层边缘房间受火(工况一),一层边缘及中间房间同时受火 (工况二),见图12。
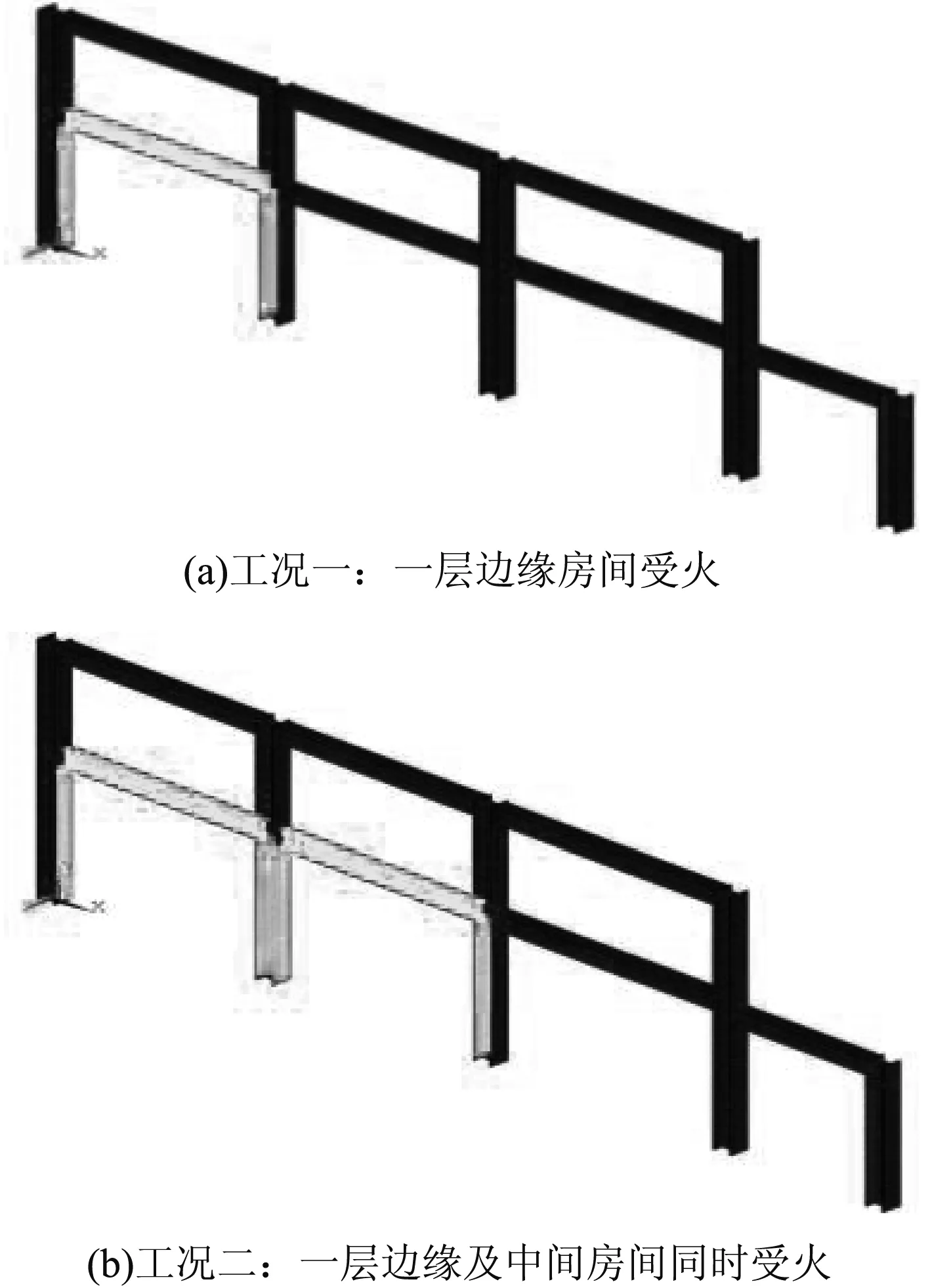
图12 不同工况下的受火位置
在进行传热学分析时,假定梁和柱的构造形式如下:柱的腹部有砖墙或隔板,因此,仅朝防火间的翼缘受到热作用。梁上部托混凝土楼板,因此,除上翼缘外的所有表面均受到热作用。热量以对流和辐射的形式从热空气传递到结构表面,又以传导的形式在结构内部传播。
3 研究结果
3.1 温度场分析
3.1.1 一层边缘房间受火
一层边缘扁间受火,钢框架的不同时刻温度云图如图 13所示。
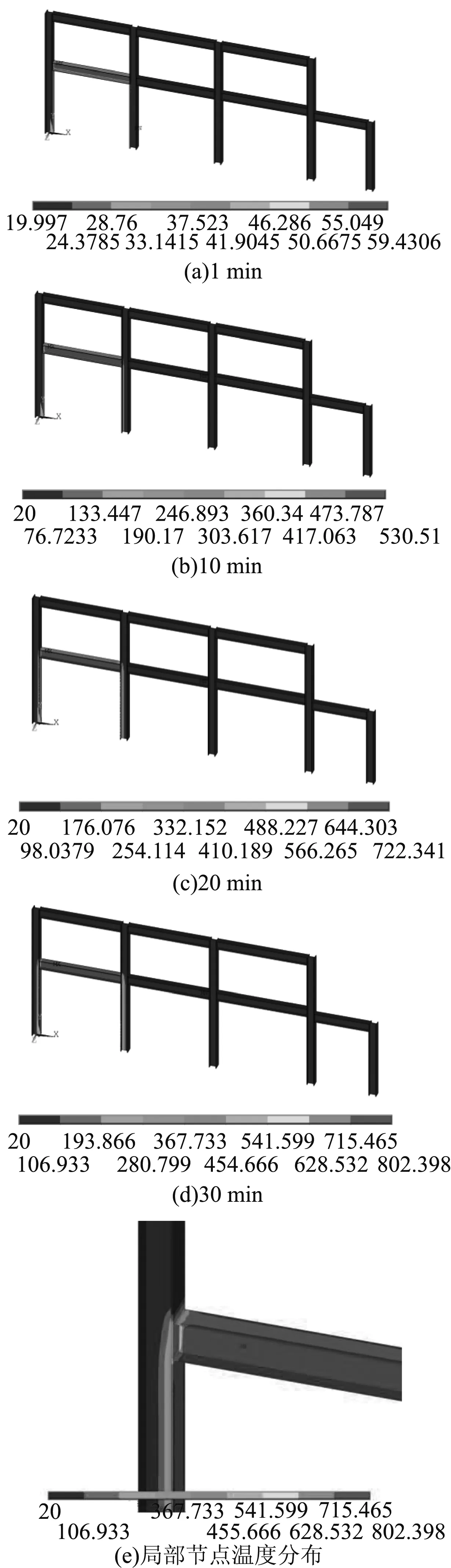
图13 一层边缘房间受火时钢框架不同时刻的温度云图
采用SOLID70三维八节点体单元,定义导热系数、比热容、密度等热分析材料特性;定义截面尺寸,建立钢框架的模型。定义受火作用的边界,对受火边界施加热辐射、热对流;定义瞬态分析的初始温度为200 ℃,初始步长为20 s,然后按照ISO 834标准升温曲线对构件进行温度计算,得出每个荷载步(时间)下钢框架沿截面和长度范围内各个点的温度,钢框架相应时刻的温度云图。
由图13可知,一层边缘房间受火,随着受火时间的延长,结构钢框架的局部构件温度持续增长,当受火时间为10 min时,钢框架构件的最高温度达到530.5 ℃,在20 min时,构件最高温度达到722.34 ℃,在受火时间到达30 min时,构件的局部最高温度已经达到802.39 ℃。GB 50017—2017《钢结构设计标准》和GB 51249—2017《建筑钢结构防火技术规范》要求在标准升温曲线工况下,无防火保护结构钢构件在受火30 min后的理论最高温度为829.6 ℃。可见钢框架在受火30 min时的最高温度与理论最高温度偏差在3.2%左右,基本满足要求。不同受火位置温度曲线如图14所示。

图14 一层边缘房间受火时不同受火位置的温度曲线
由图14可知,受火的腹板与下翼缘温度变化趋势相似,其中腹板温度略高于下翼缘,最终在30 min时,腹板温度高于下翼缘40 ℃。在非受火的上翼缘,其温度上升主要来源于热传导及热对流,因此温度明显低于受火区域,最终温度为702 ℃,与最高区域温度相差100 ℃。
由图13结构钢框架的温度云图也可以看出,在距离受火区域较远的梁柱构件,其温度升高速度较慢,尤其是二层梁柱等位置,其梁柱构件温度基本始终保持初始值,且结构的最低温度也在这片区域范围内。这是因为非散热面构件的热能是通过与温度较高散热面构件之间的热传递作用获得的,并且热传递所传输的能量多少会随着传递路径的增加而衰减。因此,距离受火区较远构件的温度基本保持常温状态。
3.1.2 一层边缘及中间房间同时受火
考虑两间相邻房间同时受火,使用ANSYS软件进行热分析,得出每个荷载步(时间)下钢框架沿截面和长度范围内各个点的温度。钢框架相应时刻的温度云图如图15所示。不同受火位置的温度曲线如图16所示。

图15 一层边缘及中间房间同时受火时钢框架不同时刻的温度云图

图16 一层边缘及中间房间同时受火时不同受火位置的温度曲线
由图16可知,受火的右侧梁跨中下翼缘及腹板的温度变化与单间受火情况的温度变化规律一致,且同时刻腹板温度都略高于中下翼缘温度,在受火30 min后腹板温度798 ℃,中下翼缘温度782 ℃,相差16 ℃。受火的公共梁柱顶部与侧 柱中点的温度均随着受火时间的延长稳步上升,20 min时梁柱顶部温度为475 ℃,侧柱中点位置温度568 ℃。
3.2 结构变形及力学性能分析
3.2.1 结构变形分析

图17 不同工况下受火30 min后的结构位移云图
工况一。受火30 min后结构变形如图17(a)所示,沿X轴方向,结构的位移极值发生在一层最左侧的柱顶位置,大小为46.62 mm。沿Y轴方向,结构的最大位移发生在左侧一层梁的跨中位置,大小为39.86 mm。沿Z轴方向的位移很小,可以忽略。最终整体结构的最大位移发生在一层的柱顶位置,极值为46.65 mm。
工况二。受火30 min后结构变形如图17(b)所示,与单间受火不同,沿X轴方向,最大位移出现在左侧受火房间的左侧梁柱顶部,大小为63 mm。沿Y轴方向,结构的最大位移还是出现在受火梁的跨中位置,在两间受火房间都出现梁跨中的向下变形,最大值为32.87 mm。最终整体结构的最大总位移发生在受火两间房的公共梁柱节点位置,极值为92.72 mm。
不同于单间房间受火,相邻房间同时受火时,结构出现平面外失稳,在受火30 min时,不加平面外约束的情况下,Z方向变形最大为86.51 mm,位于公共梁柱节点柱顶位置,结构在受火公共节点位置出现明显的巨大内陷。
3.2.2 力学性能分析
不同工况下受火30 min后钢框架的力学性能如图18所示,钢框架不同位置的最大变形曲线如图 19所示。

图18 不同工况下受火30 min后钢框架的力学性能

图19 不同工况下受火30 min后钢框架不同位置的最大变形曲线
由图18可知,当结构受火30 min后,受火区域的柱结构整体应力变大。从应力的发展过程来看,梁柱节点上部区域首先进入屈服,随着温度不断升高节点上进入屈服阶段的区域越来越多,整个过程中塑性区不断扩展。伴随着钢梁的失效,柱的应力普遍增大,增长速度最快的是柱脚部分。梁的跨中、柱脚及梁柱连接节点区域都是火灾中比较薄弱的环节,它们的“薄弱”是结构上受力和火灾发生时产生的高温共同造成的,需要重点关注。
由图19可知,左侧一层柱顶从升温开始至23 min水平位移直线增加,之后趋于稳定,30 min时为46.65 mm。梁跨中节点是向下竖向位移最大的位置,6 min内没有明显变化,6~20 min开始逐步增加,20 min后位移增加斜率增大,30 min时位移值为39.86 mm。左侧边柱中点是竖向位移向上的最大点,为7.11 mm。
3.3 火灾后钢框架结构性能评估
在火灾下,结构的整体承载能力极限状态的判别标准如下。
(1)结构丧失整体稳定性。

当一层边跨及中间房间同时发生火灾时,在0~16.6 min时,水平位移不断增大,最终达到63 mm;结构受火膨胀,受火位置之上的结构柱竖向位移一直在缓慢平稳增加,最大值为31.37 mm。梁跨中竖直向下的位移在16 min之前较小,16.6 min以后快速增加,在30 min达到32.87 mm。平面外的位移在20 min之前并不明显,20 min以后发生剧烈变形,在20~30 min内快速产生86.51 mm的变形。当挠度为20 mm时,对应的时间为23.3 min,此时的梁跨中温度约为642 ℃,此时结构已经出现平面外失稳情况,Z向位移为25mm。
4 结语
(1) 不同火源模式下,结构不同位置的温度、变形、力学性能明显不同,其中,梁跨中、柱脚及梁柱连接节点为抗火薄弱环节。
(2) 梁下翼缘及腹板高于上翼缘及柱受火面,不同火源模式下的温度变化趋势趋于一致,但是由于框架不同位置约束情况不同,因此受火后的结构变形存在差异。
(3) 一层边缘房间受火时结构破坏耐火时间为21.6 min,一层边缘及中跨房间同时受火时,16 min之后结构变形迅速升高。因此钢框架单跨受火时需要在20 min内迅速采取措施控制火情,双跨同时受火时则需要在16 min内采取措施控制火情,减轻对框架整体的破坏。
另外,出于最大安全考虑,本文未考虑防火涂层材料对结构整体抗火的影响。实际工程中会通过使用绝热、耐火材料来阻隔火焰直接灼烧钢结构,降低热量传递的速度,以推迟钢结构升温、强度变弱的时间等,进而将钢结构的耐火极限提高到设计规范规定的极限范围,防止钢结构在火灾中迅速升温发生形变塌落。针对涂层材料、涂层结构等有必要进一步深入研究。

