阵风工况下多台风力机尾流效应的非定常特性

曹九发，宋佺珉，王超群，朱卫军，柯世堂

(1. 扬州大学 电气与能源动力工程学院，扬州 225127；2. 丹麦科技大学 风能系，丹麦 哥本哈根 灵比 2800；3. 南京航空航天大学 民航学院，南京 210016)

0 引言

风力机尾流影响是风电场的选址和布局设计中的一个重要考量因素。在风电场的整体布局中，一部分风力机不可避免地会处于上游风力机的尾迹中，由此带来的直接影响是位于尾迹中的风力机发电量降低，同时尾流效应带来的风切效应和湍流增强等因素增加了尾迹区风力机的疲劳载荷。丹麦某个海上风电场的测试研究中发现，由于尾流效应的影响，整个风电场的发电功率损失可达到总装机功率的10%～20%[1]。风力机工作在非稳态的复杂来流环境中，其性能会受到较大影响，尤其是极端风况阵风（即风速在短时间内产生剧烈波动），会导致风力机气动载荷发生破坏性波动，影响风力机的运行安全和使用寿命。因此，研究风力机尾流特性及上下游风力机的载荷特性，着眼于提高发电效率、减少尾流对风力机性能的影响，对风电场高效健康运行具有十分重要的意义。

目前风力机尾流研究主要有实验研究和数值模拟研究。国内外很多学者[2-4]对风力机尾流进行了PIV实验研究，得到了尾流流场数据，但是实验研究大多为缩比模型的风洞实验，而风力机尾流的场外实验，特别是针对多台风力机在复杂非稳态工况下的尾流干扰实验研究，成本较高，难度大。随着计算方法及设备性能的日益发展，CFD已经成为研究风力机尾流效应和尾流干扰的常用手段[5-9]。近年来，致动理论耦合CFD方法成为风力机尾流数值模拟方法的热点[10-12]。该耦合方法将风力机叶片的气动力作为体积力源项加载到流场中，然后通过求解N-S（Navier Stokes）方程来获得流场信息，这种方法相对于传统具有叶片物面网格的方法，可以大大提高数值计算效率。致动理论模型主要有致动盘（Actuator Disk，AD）、致动线（ Actuator Line，AL）和致动面（Actuator Surface，AS）模型。丹麦科技大学的Sørensen[13]在致动盘模型的基础上发展出了风力机尾流模拟的致动线模型，并采用自主研发的EllipSys3D求解器，对比了风力机在大气湍流和均匀来流下的尾流特性。Zhu等[14]采用EllipSys3D求解器，研究了在叶片根部、风轮前方增加导流盘后风力机功率的变化。Shen等[15]将致动线模型与N-S/LES（Large Eddy Simulation）耦合，然后基于MEXICO风力机实验数据，开展了风力机尾流数值模拟方法的改进研究。朱翀等[16]以NH1500 叶片为研究对象，采用RANS（Reynolds Averaged Navier-Stokes）结合k-ωSST湍流模型的方法，从叶片载荷分布和功率系数两个方面将致动线方法、叶素动量理论、叶片物面网格方法进行了对比，同时分析了风力机尾流速度变化特性与气动载荷特性。Qian等[17]采用 ALM-LES 方法，模拟了风力机尾流的高精度湍流流动结构及气动载荷。卞凤娇等[18]基于OpenFOAM 平台，对比了PISO求解的致动线模型和多重参考稳态求解的CFD实体模型，进而采用致动线模型数值研究了NREL 5 MW风力机在均匀来流中的尾流场特性。Nathan等[19]比较了采用OpenFOAM和EllipSys3D求解器求解致动线模型的结果，并将其与NEW MEXICO实验数据进行对比，结果表明两者均能在近尾流处较好地吻合实验数据。周洋等[20]比较了致动线方法中均匀分布和高斯分布两种不同的体积力分布方式，并分别采用这两种方式对Nibe A型风力机进行了数值模拟，得到了高斯分布方式更接近实验数据的结论。目前风力机尾流效应研究和尾流干扰研究主要是针对稳态工况开展的，本文则计划针对风电场非定常阵风入流工况，采用LES耦合致动线模型的方法，开展多台风机的尾流特性、尾流效应及风力机动态气动载荷的相关研究。

1 数值模型与方法

1.1 N-S/LES模型

数值模拟的控制方程采用三维不可压N-S方程。连续性方程为：

对于三维不可压缩牛顿流体，动量守恒方程为：

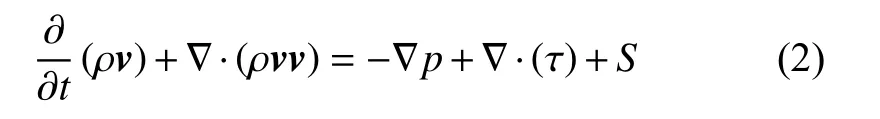
其中：v为 惯性坐标系下的速度矢量；t为时间；ρ为密度；p为静压；τ为应力张量；S为添加的体积力动量源项，本文主要是风力机叶片产生的气动力。

τ由下式给出：

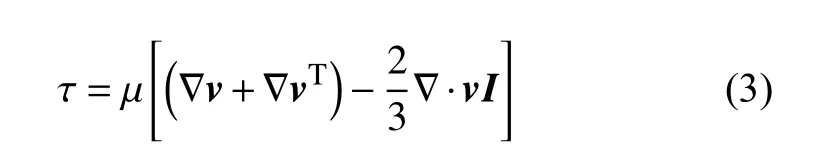
其中 µ为分子黏性系数，I为单位张量。

LES大涡模拟是求解瞬态流动的主要方法之一，它是在空间域上对瞬态Navier-Stokes方程进行滤波处理。滤波过程可将小于滤波器宽度或计算网格尺度的小尺度涡过滤出去，从而形成关于大尺度涡的控制方程。在LES方法中，通过使用滤波器函数，将每个变量都分成两部分—大尺度分量和小尺度分量。大尺度部分是滤波后的变量，是在LES模拟时直接计算的部分；小尺度部分是需要通过模型来表示的。滤波处理后，瞬态状态下的N-S方程包含了如下新的应力项：

式 中， τij被 定 义 为 亚 格 子 尺 度 应 力（Sub-Grid-scale Stress，SGS），体现了小尺度涡的运动对所求解的运动方程的影响。 τij是一个对称张量，其包括6个独立的未知变量。对 τij进行不同的建模，就可以得到不同的SGS模型。本文采用Smagorinsky-Lilly模型进行风力机尾流流场的LES数值模拟。整个风力机流场数值求解流程如图1所示。

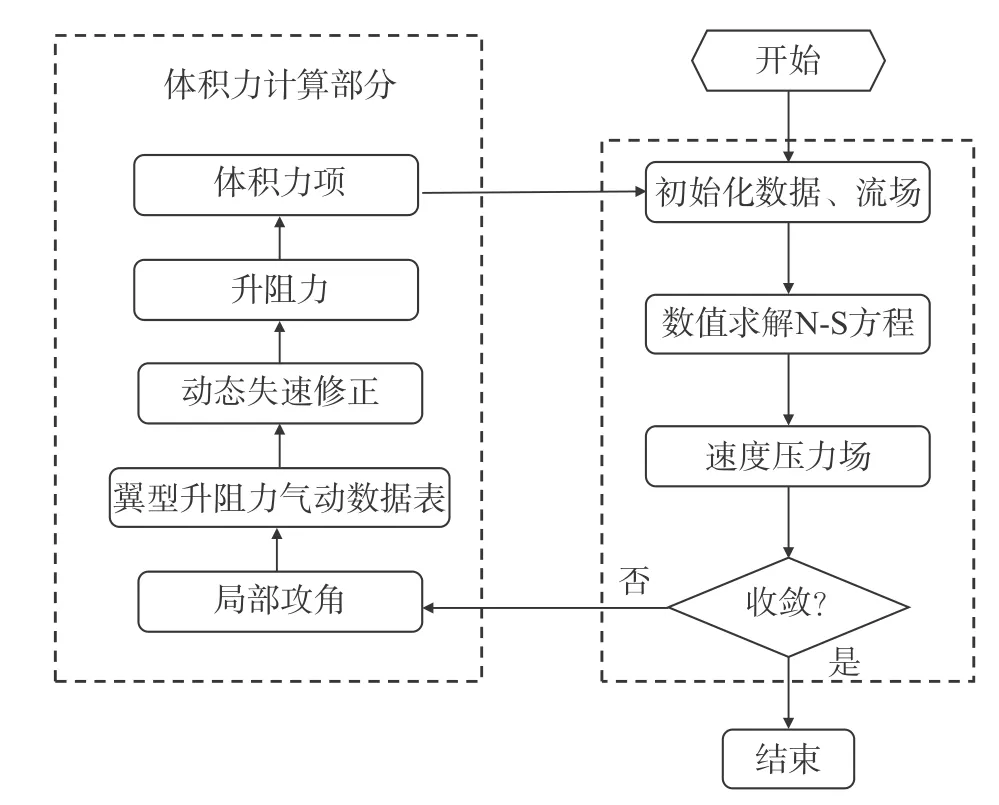
图1 致动模型与N-S方程耦合计算流程图Fig. 1 Flow chat of the actuator line model coupled with the N-S equations

1.2 致动线模型AL

风力机的致动线模型是基于风力机的叶素动量理论延展出的等效风力机叶片模型[15]。如图2所示，将叶片分成一个个微元段（叶素），根据当地的流场信息与已知的翼型性能数据、叶片外形数据，可求得每个叶素上的气动力。图2最右边为某个叶素的截面图，x为来流方向。

图2 致动线模型示意图Fig. 2 Schematic of the actuator line model

叶片翼型截面的当地速度[15]为：

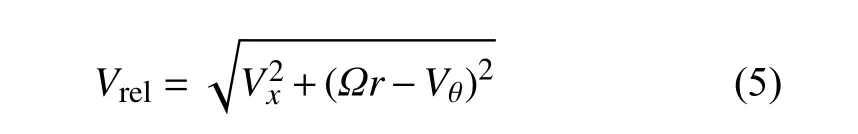
其中， Ω为风轮转动的角速度，r为截面翼型到叶根的位置，Vx和Vθ分别为翼型的轴向速度和切向速度。

翼型截面当地速度与风轮平面夹角为入流角，

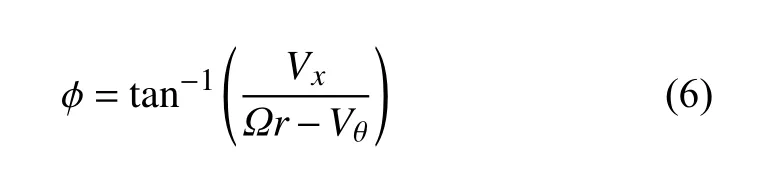
翼型截面的当地攻角为入流角减去桨距角γ，

确定了叶片翼型的当地速度与攻角后，即可求出叶片单位展长的升力与阻力：

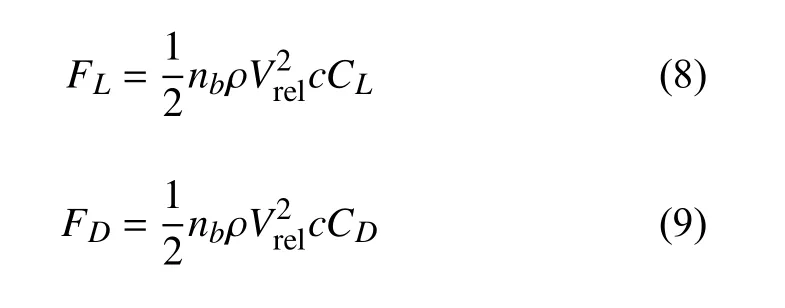
其中，nb为 叶片数，CL和CD分别为升力、阻力系数，c为翼型弦长，ρ为空气密度。

为了考虑机舱和塔架对风力机尾流流场的影响，也可把机舱等效于体积力源项来模拟。机舱体积力计算公式为：

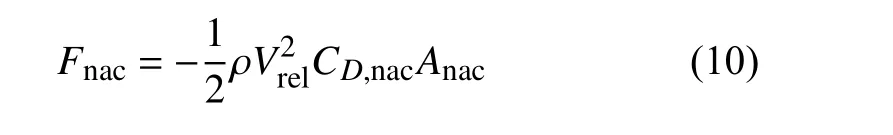
其中：CD,nac为机舱阻力系数（取值范围一般为0.8～1.2），本文取值1.0；Anac为机舱的横截面积。

参考风力机叶片叶素理论方法，可以把塔架同样分成一段段单个长度为dh的微元。任意一段微元处的轴向阻力为：

式中：CD,tower为塔架阻力系数（取值范围一般在0.8～1.2），本文取值1.0；dtower为微元段塔架直径。

确定了所有体积力之后，需要将计算出来的力光顺到叶素点周围的网格中去。为了防止求解时发生数值震荡，本文采用三维高斯分布将体积力光顺过渡到周围的网格上：

其中：dm为叶素点到网格型心的距离；ε为高斯分布因子，该参数取值与风轮旋转加密区网格单元尺寸Dm有 关，即ε=nDm，n为倍数，本文取n= 2。

1.3 阵风

风况是结构完整性设计主要考虑的外部条件。从载荷和安全角度考虑，风况可分为风力发电机组运行期间通常的正常风况以及按1年或50年重复周期确定的极端风况。极端风况包括由于风向和风速急速剧烈变化产生的峰值风速，因此在设计时需要对其影响加以考虑。一般采用极端风况确定风力机的极端载荷。

对标准等级风力机组，根据IEC61400-1风力发电设计要求规范，轮毂高度处的重复周期为N年的阵风幅值关系式如下：

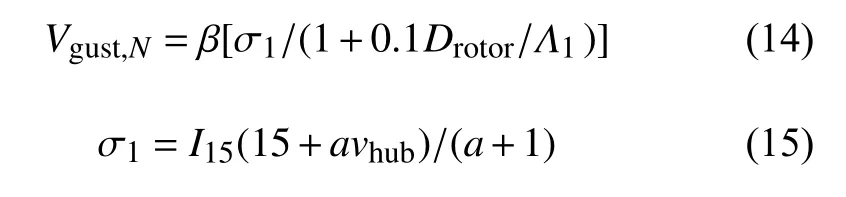
式中：I15= 0.18，a= 2，为较高湍流强度类别；I15= 0.16，a= 3，为较低湍流强度类别。本文选取较高湍流类别。 Λ1为湍流尺度参数，取值由下式给出：

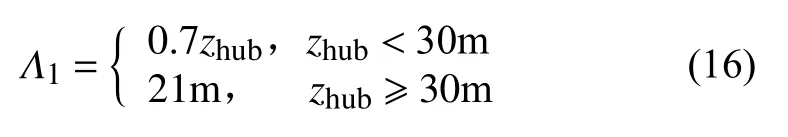
其中：Drotor是风轮直径；β = 4.8，对应N= 1； β = 6.4，对应N= 50。

当重复周期为N年时，由下列方程确定风速：

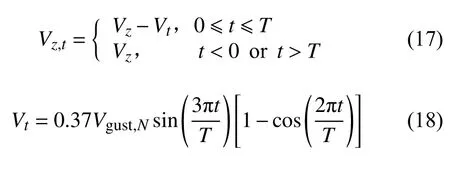
式中：Vz选用风切；T= 10.5 s，对应N= 1；T= 14.0 s，对应N= 50。本文选取T= 10.5 s。

图3为极端运行阵风示意图，假设正常风速为11.4 m/s（亦为本文作为边界条件的输入风况）。ag点表示正常风速值的位置，bg、dg点为阵风周期内风速最低的时间点位置，cg点为阵风周期内风速最高的时间点位置，eg点表示阵风周期结束后风速回归到正常风速值的位置。

图3 阵风示意图Fig. 3 Schematic of the gust wind

2 结果与分析

2.1 算例验证

本文以丹麦Nibe风力机作为致动线模型数值模拟的验证算例。Nibe风力机的主要参数见表1，具体的叶片、轮毂和塔架参数等见文献[21]。

表1 Nibe B风力机主要参数信息表Table 1 Key parameters of the Nibe B wind turbine

计算采用如图4所示的长方体计算域，计算域的长、宽、高分别为24.5R、6R、6R。对转子所在的区域进行局部加密，加密范围为：x方向，风轮平面前后0.5R；z方向，轮毂中心左右1.5R；y方向，轮毂向上1.5R。加密区以外的单元，网格按照一定的比例向外延伸。风力机转子中心在（0，45，0）位置。整个计算域总网格量为430万，均采用六面体正交网格。

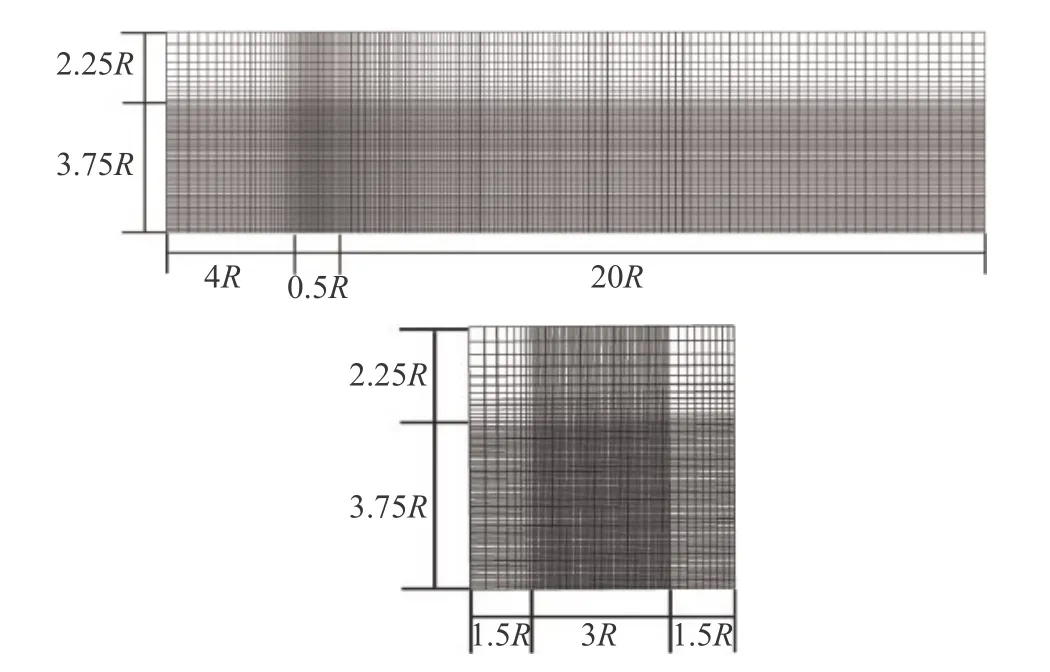
图4 计算域网格示意图Fig. 4 Schematic of the computational domain and grid

风力机的叶片被分为20段，每一叶素段长度为1 m，恰好与加密区的网格单元尺寸相同。在计算时，取三维高斯分布参数ε= 2 m。Nibe风力机位于丹麦北部沿海地区，西侧为浅水区，东侧为以矮草为主的平坦地形，可认为来流风速不受地形影响。因此，根据实验[21]工况，入口速度边界速度为8.0～9.1 m/s工况（本文选取8.55 m/s），湍流强度为10%～15%（本文选取10%），其中入口风速考虑风剪切效应，出口边界设置为压力出口，下边界为物面，上边界为滑移边界，左右边界设置为滑移边界。对采用笛卡尔正交坐标系的致动线模型而言，非定常数值计算的时间步长由风轮转速确定，即单个时间步内叶尖旋转的距离不能大于所在区域的网格单元尺寸，Dm： ωrdt≤Dm。在本算例中，时间步长为dt≤ 0.006 s，总共模拟400 s，尾流风速由200～400 s数据取平均值得到。

图5为Nibe风力机在轴向上不同位置处的速度剖面图。通过与实验测量值对比，可以看出：风力机尾流速度在轴向位置上呈现出抛物线特性的变化趋势，轮毂中间位置存在速度最低点；随着轴向位置的增加，风力机尾流速度不断恢复，这是由于随着轴向距离增加，周围大气向尾流中心不断进行能源补充，使得速度逐渐向来流速度值恢复。从图中也可以看出，本文的计算方法，不仅近尾流区的速度计算结果有较好的准确度，而且在比较重要的远尾区，计算结果与实验值吻合较好。因此，本文的非定常致动线模型耦合LES的风力机尾流数值计算方法，具有较好的准确性和可行性。

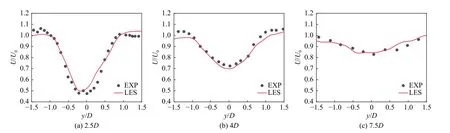
图5 不同位置的风力机尾流的剖面速度对比图Fig. 5 Velocity profile comparison at different locations of the wind turbine wake

2.2 NREL 5 MW阵风工况数值计算

2.2.1 边界条件和计算域

NREL 5 MW风力机主要参数见表2，具体的叶片和翼型数据可参阅文献[22]。

表2 NREL 5 MW风力机主要参数信息表Table 2 Key parameters of the NREL 5 MW wind turbine

图6为流场计算区域示意图。在长、宽、高分别为17D、3D、3D的长方体计算区域中串列布置3台水平轴NREL 5 MW风力机，沿流向分别记为WT-1（第一台风力机）、WT-2（第二台风力机）、WT-3（第三台风力机）。网格在风力机附近区域进行加密，加密区的长、宽、高分别为0.5D、1.5D、1.5D，加密区网格单元尺寸为2.04 m。为了捕捉到涡系的细微结构，在风力机尾流区采用全加密方式，计算总网格量为1100万。风力机叶片、机舱和塔筒均用体积力源项表示，其中叶片的分段数为30，塔筒的分段数为45。三台风力机中，WT-1距离入口2D，WT-3距离出口5D，每台风力机之间的距离固定为5D。

图6 计算域示意图Fig. 6 Schematic of the computational domain

2.2.2 非定常阵风计算工况

计算采用如图3所示的来流阵风工况，正常平均风速为11.4 m/s，阵风周期为10.5 s，计算时间段分为两部分：第一部分仿真时间0～220 s，参考风速为轮毂风速11.4 m/s；第二部分仿真时间220 ～500 s，入口边界条件为阵风条件。选取五个时间点所对应的纵向瞬时速度云图（图7），分别为：阵风来流前215 s、阵风遇到风轮的时刻282.5 s（bg点）、阵风遇到风轮的时刻285 s（cg点）、阵风遇到风轮的时刻287.5 s（dg点）。

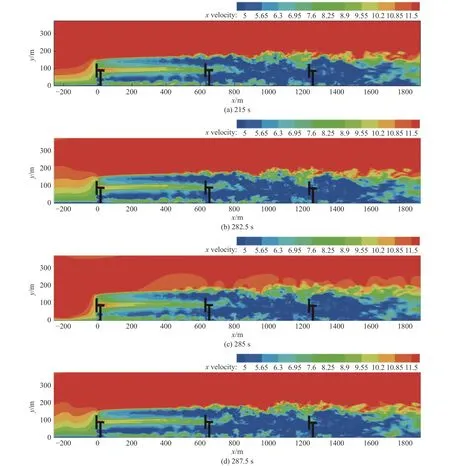
图7 不同阵风时刻的纵向中心处的速度截面云图Fig. 7 Velocity contours in the slice along the longitudinal center at different time instances under the gust wind condition

从图7可以观察到，随着轴向位置增加，风力机尾流区也随之膨胀，并且风速呈现出时间和空间的瞬时变化的特性，尾流膨胀边界在向下游发展的过程中变得越来越不清晰。由于受到风剪切的影响，整个尾流区中在纵向上出现了靠近地面的流速小于轮毂以上的流速，尤其是在第一台到第二台风力机之间表现得更为明显。受下游风力机的影响，第一台风力机的尾流来不及恢复就再次发生流速的降低，从而整个尾流区只有最后的区域出现了流速的恢复现象。此外，对比不同时刻的阵风速度云图，可以发现，当阵风处于高点cg时，尾流膨胀较正常来流时更加明显。

图8为阵风经过时的尾流流场涡量云图，采用的是Q准则，Q值取0.0005。图8（a）为三台风力机在没有阵风入流工况下的尾流涡系结构图，可以看出，叶尖涡卷起并逐渐向下游发展。近尾流的叶尖涡系结构明显。随着涡系的发展，出现了涡混合和涡破碎现象，特别是在第二台到第三台风力机位置，涡已经完全混合，并且随着尾流中的湍流强度的增加，尾流中的涡系受到风剪切的影响，导致上下涡倾斜往下游发展。随着时间的推移，阵风入流开始影响尾流涡系结构，图8（b）可见叶尖涡间距开始发生改变，图8（c）中叶尖涡系开始变大并向下游移动，并且导致尾流区出现更大的膨胀；图8（d）阵风涡系也同样发生了涡破碎和涡融合现象，同时产生尾流速度瞬时变化和湍流强度变化。对比图8（a）可以发现，阵风涡系的叶尖涡涡核更大，并且叶尖涡之间的间距更宽。

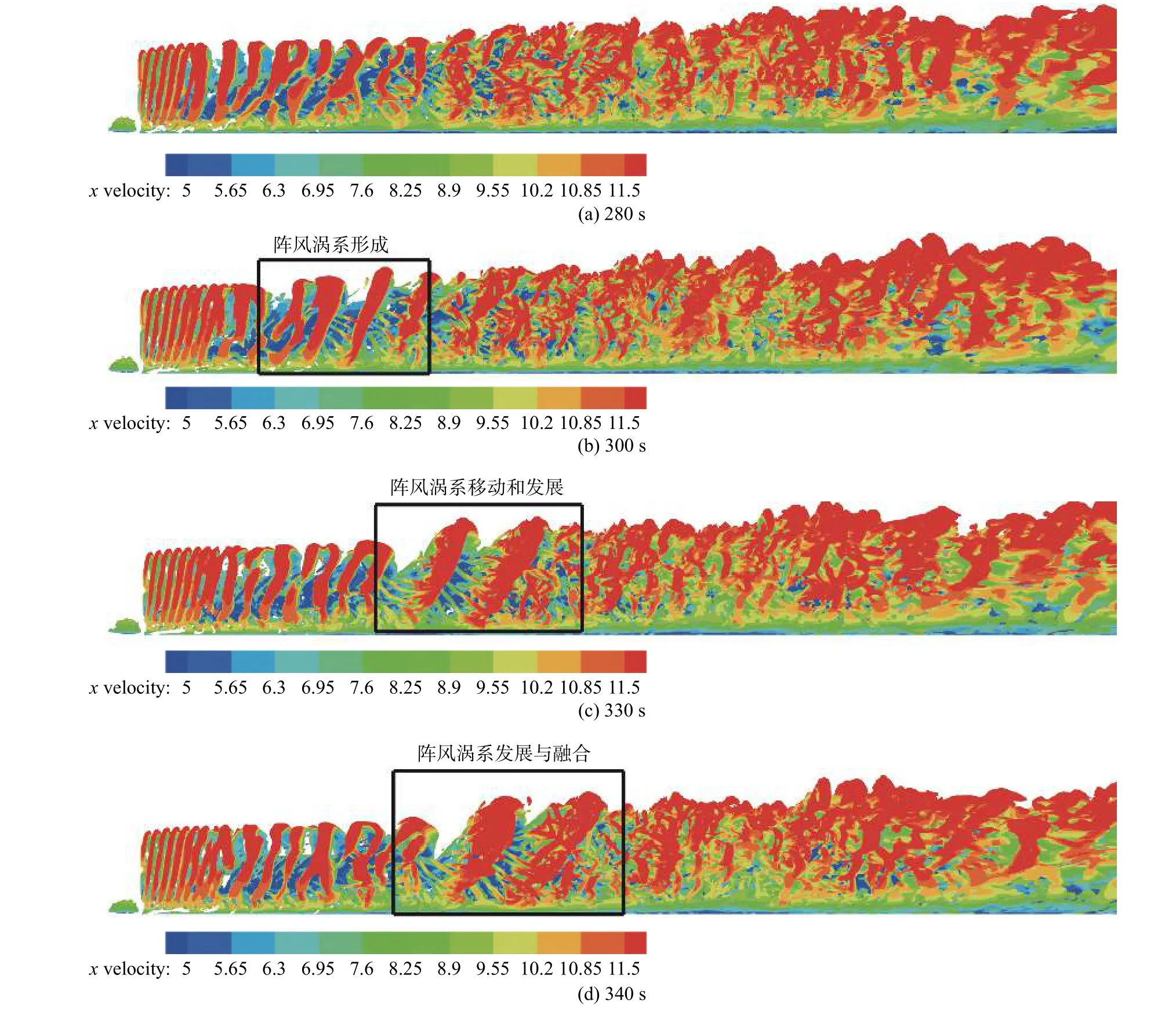
图8 不同阵风时刻的由速度染色的涡等值面（Q = 0.0005 ）Fig. 8 Vortex iso-surface (Q = 0.000 5) colored by the velocity at different time instances under the gust wind condition

图9是遭遇阵风之后三台风力机的输出功率及风轮推力对比图，数值模拟中假定风力机来不及变桨。由图可见，受阵风影响，功率及轴向推力较平稳周期的响应值出现了较大幅值的周期性波动，尤其是第一台风力机的功率及轴向推力曲线出现了明显的一个峰值和两个谷值。对于第二台风力机，由于上下游风力机之间存在尾流效应和尾流干扰，因此阵风入流后，第二台风力机气动载荷（功率和推力曲线）出现了两个比较明显的峰值突变，此时阵风的响应时间在第335 s左右，阵风响应结束时间大概在第390 s，是入流阵风周期的5倍左右，可见，阵风速度和尾流效应的耦合作用导致了第二台风力机的阵风气动载荷作用周期延长，同时曲线会出现两个峰值，这个结论对于评估风力机载荷性能具有重要参考意义。第三台风力机的输出功率相对于第二台出现了回升，这是因为，随着尾流的发展，尾流与外界的空气混合及能量交换加快，从而导致风速恢复速度变快。对比不同风力机的功率和推力时间曲线图，可看出，第三台风力机的气动载荷波动幅度较大，这是由于风力机尾流发展带来的湍流强度的增加，使得第三台风力机来流速度的湍流强度增加，同时当阵风传递到第三台风力机时，风力机对阵风的响应周期继续拉长。由表3可见，第三台风力机发电功率值回升，在有/无阵风的情况下，第一台风力机承受的推力载荷最大，第二台和第三台风力机的推力载荷值分别增加9.1%和21%。

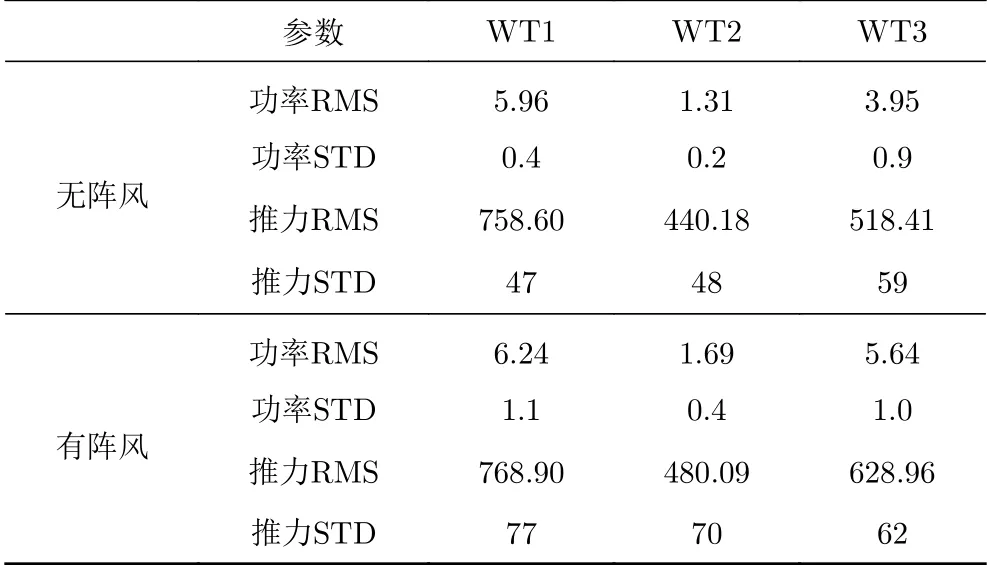
表3 有无阵风功率和推力的RMS与STD标准方差Table 3 RMS and STD values of the power and thrust under the gust and non-gust wind conditions

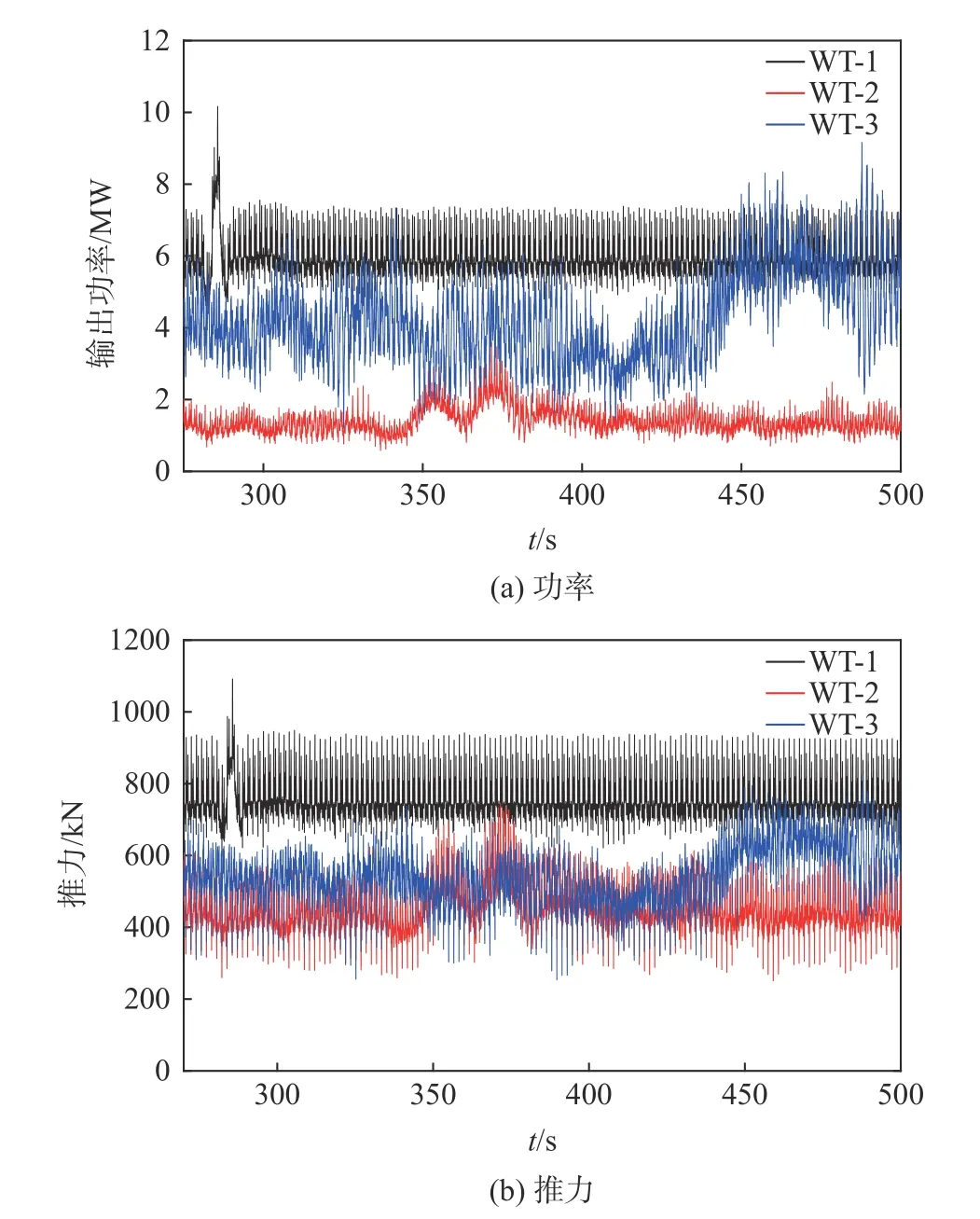
图9 三台风力机输出功率和轴向推力对比图Fig. 9 Comparison of the power and thrust of the three wind turbines

3 结论

本论文建立了 LES 耦合致动线模型的方法，并加入非定常修正，考虑了风力机机舱、塔架和风剪切等因素影响，实现了风力机非定常工况的数值模拟仿真，开展了阵风入流工况下的多台风力机尾流的涡系结构演变规律和气动载荷变化规律研究。得到结论如下：

1）基于Nibe风力机实验数据，验证了 LES 耦合致动线模型方法的可行性及有效性，模拟结果也表明，该方法在近尾流区和远尾流区都可以获得较好的尾流速度计算结果。

2）随着轴向位置的增加，风力机尾流区也随之膨胀，尾流速度出现先降低再恢复的发展特性，尾流区膨胀边界在向下游发展的过程中变得越来越不清晰。阵风使得尾流区会比正常来流时尾流膨胀得更加明显，即尾流周向直径变大。

3）成功捕捉到了阵风涡系结构。阵风会导致叶尖涡的涡间距变大，并且在逐渐向下游发展的过程中叶尖涡核也变得更大，涡破碎和涡混合更易发生。

4）阵风入流对第一台风力机的影响比较明显。而第二台风力机在尾流效应和阵风耦合的影响下，气动载荷曲线出现了两个峰值，下游阵风响应周期增加为入流阵风周期的5倍。虽然第一台风力机推力载荷最大，但是第二台和第三台风力机在阵风的影响下，推力载荷也分别增加了9.1%和21%。

5）本文研究内容及结论对风电场布局和风力机载荷强度设计具有指导意义。