改进SIFT算法在医学图像配准中的应用研究

陈宗桂，董晓军，曾令容，张英俊

(湖南医药学院，湖南 怀化 418000)

0 引 言

医学影像设备在近十年中得到迅速的发展，并广泛应用于临床诊断和治疗中。由于不同影像设备存在多种成像模式如解剖成像和功能成像。CT成像设备采集的图像为临床医师提供解剖形态信息，分辨率高。核医学成像设备采集的图像为临床医师提供功能代谢信息，但是图像模糊，分辨率差[1-2]。通过图像配准技术把不同成像模式下表达的影像信息融合在一起，给医生提供更丰富的临床信息，以提高临床疾病的诊断和治疗水平。为此，许多人员对图像配准算法进行大量研究，提出很多改进的算法，如基于面积的算法[3-4]、聚类算法[5-6]、特征检测算法、结合矩阵降维处理算法[7]、差分搜索算法[8]等。但是这些匹配算法都有一个共同点：对尺度变化、旋转变化、光照变化和仿射变换等方面的图像配准存在局限。Lowe等[9-10]在尺度空间理论的基础上提出高效且稳定的尺度不变特征变换算法，即SIFT(scale invariant feature transform)。SIFT算法是一种检测和描述图像局部特征的方法。它是通过寻找一种空间变换，使在不同时间点、不同视角或由不同探测器采集同一场景的两幅图像之间的对应点达到空间位置的一致[11-13]。在医学图像处理中，当一种成像设备采集的影像信息不能满足临床诊断需要时，可以把不同模式下的成像融合在一起。例如，通过医学图像配准把MR设备上采集的软组织信息和PET设备采集组织的功能代谢信息融合在一起[14-15]。刘璐等采用尺度不变特征变换算法对所获取的疵病图像进行配准、拼接，得到完整的疵病图像。研究结果表明SIFT算法可以高效完成图像配准，具有较好的稳定性，并且配准精确度高[16]。该文在传统SIFT算法的基础上采用32维特征向量对关键点进行描述，同时采用随机抽样一致算法剔除不稳定的点。为了提高计算机处理的工作效率，通过双向匹配保留有效的关键点，这使得关键点数量可控，精度高。

1 SIFT算法关键点提取

在图像配准中，通过尺度变换特征不变算法提取两幅图像特征点。该算法是在不同的尺度空间中寻找极值点，并通过高斯差分函数在极值点的二阶泰勒展开式精确确定极值点的位置和尺度。然后以关键点为中心，在8×8的采样窗内，计算每一个4×4的模块内8个方向的梯度累加值即特征描述符。最后，计算两幅待配准图像上关键点的相关性。该算法提取关键点的过程如图1所示。

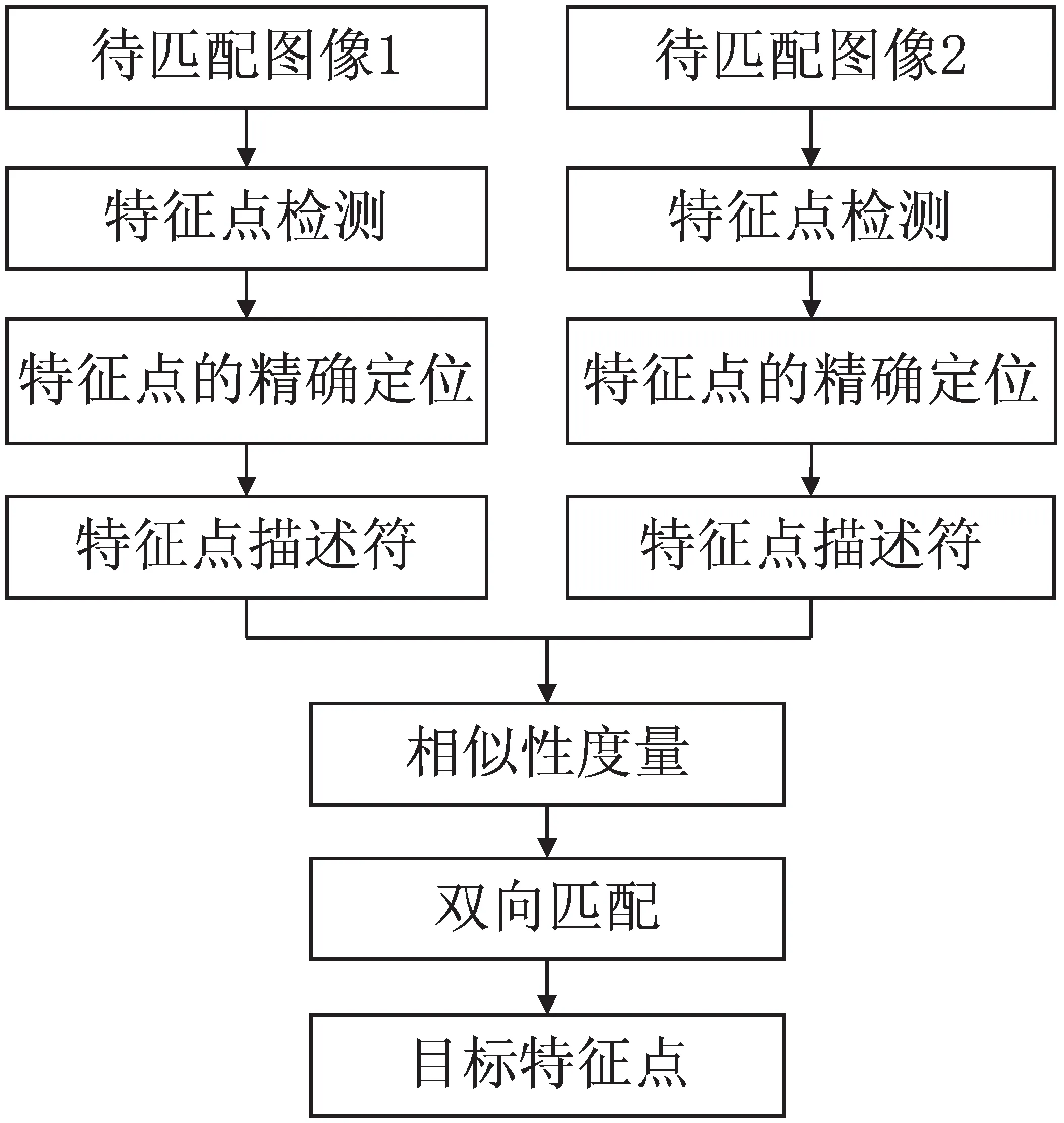
图1 SIFT算法流程

1.1 构建图像的高斯差分空间

高斯金字塔的目的是在不同的尺度空间上查找极值点以得到尺度不变的特征点。多尺度空间是不同高斯核与原图像滤波后产生，是尺度空间的一种表现形式。一个图像的尺度空间L(x,y,σ)可表示为原图像I(x,y)与一个可变尺度的2维高斯函数G(x,y,σ)的卷积运算，如式(1)：

L(x,y,σ)=G(x,y,σ)*I(x,y)

(1)

(2)

式中，G(x,y,σ)是尺度可变高斯函数，(x,y)是像素点的位置坐标。σ大小决定图像的平滑程度，它是构建不同尺度空间的关键。为了得到不随尺度变化的特征点，需要选择合适的尺度因子平滑进而建立尺度空间。

高斯差分金字塔的构造如图2所示。

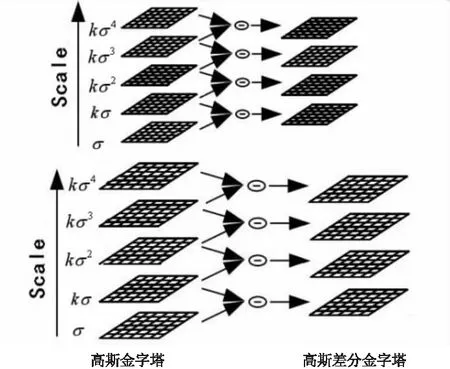
图2 高斯金字塔图像及高斯差分图像的构建

通过不同的高斯函数与原图像进行高斯卷积，得到高斯金字塔图像的第一阶。第二阶图像是对第一阶图像降采样得到。以此类推，后面每一阶图像都是由先前那一阶图像降采样得到。为了有效检测不同尺度空间上稳定的极值点，该算法使用了高斯差分(difference of Gaussian，DoG)尺度空间即相邻两尺度空间函数之差。根据式(3)将同一阶相邻图像两两相减得到高斯差分函数。

D(x,y,σ)=[G(x,y,kσ)-G(x,y,σ)]*I(x,y)

=L(x,y,kσ)-L(x,y,σ)

(3)

式中，G(x,y,σ)为差分尺度空间函数，k为尺度因子的常量系数。

1.2 不同尺度空间上关键点的检测

选某一尺度空间上的一个像素点，将该点与同一图片上相邻8个像素点和相邻尺度空间上18个相邻点进行比较。当其大于(或者小于)所有相邻点时，该点就确定为关键点。如图3所示，以黑点为检测点，将它和周围的8个灰色的点还有上一层的9个点与下一层的9个点，共26个像素点进行比较。由于检测到的关键点是离散空间上不连续的点，因此采用高斯差分函数在极值点X0=(x0,y0,σ0)的二阶泰勒展开式进行精确定位，求得极值点和特征点的偏移量，如式(4)：

(4)

其中，X=(x,y,σ)T表示极值点和特征点之间的位置和尺度偏移量。要精确定位关键点的位置，必须对式(4)求一阶偏导并让方程等于零可得：

(5)

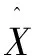
(6)

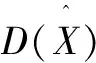
图3 不同尺度空间上的特征点检测

1.3 关键点方向赋值

为了使描述符具有旋转不变性，在以关键点为中心、3×1.5σ为半径的区域计算每一个关键点的方向向量θ和梯度幅值m。直方图以45°为间隔依次统计0°～360°内每一个关键点的梯度幅值分布，将统计结果最大值代表的方向作为关键点的主方向。

m(x,y)={[L(x+1,y)-L(x-1,y)]2+[L(x,

y+1)-L(x,y-1)]2}1/2

(7)

(8)

为了增强特征描述算子的鲁棒性，需要保留关键点的辅方向即超过关键点梯度方向最大值80%的方向。一个关键点可以有多个辅方向。

1.4 关键点描述

通过在极值点位置的二阶泰勒展开式精确确定关键点位置和尺度。为了提高配准的准确性，还需要了解关键点邻域像素对关键点的影响。因此，以关键点的主方向为基准方向，将整幅图像旋转到关键点的主方向上，以确保所得特征描述符的旋转不变性。然后，以关键点为中心取8×8的窗口，在4×4的小窗口内计算8个方向的梯度直方图，每个梯度信息就是一个描述符，如图4所示。采集窗口的中央表示采样的关键点，每个小格表示同一尺度内关键点邻域像素。其中，每一个小格内的箭头方向表示该邻域像素的梯度方向信息。最后将8×8窗口按4×4的窗口划分得到4个模块，并计算每个模块内8个梯度方向的直方图累加，如图4所示。每个模块对应8个方向的梯度信息即形成8维特征描述符。一个关键点包含4个模块，则每个关键点就对应32维特征描述符。这种结合邻域像素的方向信息对关键点方向信息的影响，提高了算法的抗噪能力和配准的准确性。对于特征匹配中需要定位的误差，也提供了一定的容错能力。此外，为了减少光照对配准的影响，对所有的特征向量进行归一化。

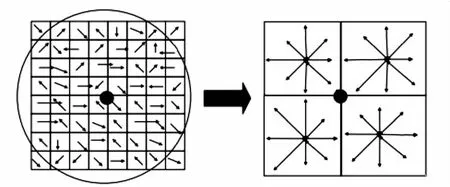
图4 图像梯度及特征点描述

1.5 关键点匹配

传统SIFT算法大都采用欧氏距离作为两个关键点的相似性度量进行匹配，并且采用遍历搜索确定关键点位置，计算量较大。为了提高检测关键点的效率和匹准精度，该文采用高维向量的最近邻搜索算法(fast approximate nearest neighbor search library，FLANN)。该算法检测效率高，计算量小。通过FLANN算法检测到关键点后，采用式(9)计算两幅待配准图像上关键点的相似性。若图像I1的关键点描述符数为M，待配准图像I2的关键点描述符数为N，根据式(9)度量两个关键点的相似性。首先计算图像I1上关键点描述符与图像I2上关键点描述符的乘积作为分子。再次，计算图像I1上关键点描述符平方和的平方根与图像I2上关键点描述符平方和的平方根，将两者的乘积作为分母。若二者比值小于阈值(取0.95～0.98)，则两个关键点配准成功；否则配准失败，如式(9)。理论上两幅图上的场景完全相同时，对应的关键点一致，相关性R=1。

R(i,j)=

(9)

式中，S和T分别是两幅图像中的关键点描述符，R是相关系数。本研究中的匹配采用的是距离比值法，可能导致出现一对多的匹配结果。因而，该文利用双向匹配，避免出现一对多的匹配结果和消除错误的关键点。其方法为：分别从图像I1和待配准图像I2上进行FLANN搜索关键点匹配。然后再从待配准图像I2到图像I1进行FLANN搜索匹配。同时计算两次配准关键点的坐标和。当两次搜索匹配结果的坐标和一致，则把两点当作匹配点，否则剔除，由此得到一一对应的关键点匹配。

2 改进的SIFT算法

本研究通过积分对图像滤波，分别用不同的积分矩形区3×3、5×5、7×7、9×9、11×11表示同一阶中的不同尺度图像。然后通过降采样得到不同阶的图像，同一阶图像两两相减得到高斯差分图像。

传统的SIFT算法每一个关键点采用128个描述符，即两幅图像就需要计算128×M维向量和128×N维向量的乘积，并对该向量的比值排序。计算耗时，算法效率低。大部分的时间都用在计算两幅图像上关键点最邻近欧氏距离的比值。为了改善这一状况，该文以关键点为中心取8×8的窗口，在4×4的小窗口内计算8个方向的梯度直方图，这样一个关键点就可以用32维的描述符表示。最后对每一个关键点的梯度向量信息进行归一化，以保证光照不变性。

传统SIFT算法在图像配准中提取大量的局部关键点，这些关键点可能只有少量具有实际意义。而多余的关键点不能反映图像的结构特征，导致数据冗余，容易产生误匹配。随机抽样一致(random sample consensus，RANSAC)算法可以剔除不稳定的点，提高配准的准确性。RANSAC算法计算过程稳定，对不满足要求的关键点进行有序性筛除，剔除错误关键点能力较好。但RANSAC算法对参数估计是通过不断进行迭代和测试完成的，且初始模型参数是对随机抽取的数据计算得到，不确定性比较大；若随机抽取的初始数据误差较大，则算法有效性被严重影响。该文采用改进的随机抽样一致性算法对所有的关键点进行测试，并把其中不满足条件的关键点对剔除。同时选择优质的关键点对作为数据集合代表，以减小模型参数不稳定性和误匹配，提高图像配准的准确性。这样不仅可以减少迭代计算的次数，而且计算得到的参数更准确。

为了提高配准精确性，在第一次关键点配准成功之后再增加一次配准。第一次配准结束后计算两个关键点行列方向的坐标和，然后交换两幅图像的顺序。第二次匹配时，再计算两个关键点行列方向的坐标和。当两次匹配得到两个关键点的坐标之和相等时，就把这两个点保留下来。研究表明经过两次匹配可以删除大量错误关键点和较大地提高配准的准确性。

3 实验仿真与结果

采用MR设备采集颅脑图像。通过MATLAB软件编写的程序实现对2幅图像配准，图像大小均为1 280×1 280。为了验证改进算法的有效性，通过传统的SIFT算法和改进的算法提取不同场景MR图像关键点，比较两种算法的运算时间和匹配率，如图5所示。左边是采用改进SIFT算法对两幅图像进行配准。改进后SIFT算法提取关键点数量减少，两幅图像特征点的配准时间也显著减少。右边是传统SIFT算法对两幅图像进行配准。传统的SIFT算法提取的关键点数量多且大部分时间都用在计算二者的拟合度。通过改进的SIFT算法对两组不同角度和不同灰阶的MR图像进行配准，效果良好，误匹配的点数为0，如图6所示。此外，为了验证改进后SIFT算法的鲁棒性，给原图像添加高斯噪声并通过本算法进行配准，如图7所示。从图7可知从两幅图像上提取的特征点完全一致，误匹配关键点数为0。改进后的SIFT算法鲁棒性较好。

(a)传统SIFT算法 (b)改进SIFT算法

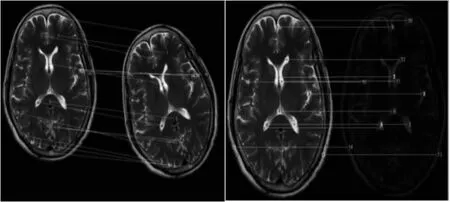
(a)不同角度的图像 (b)不同灰阶的图像

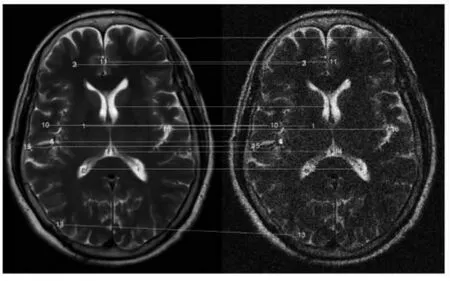
图7 原图像与添加噪声图像的匹准结果

为了测试算法运行速度，从不同步骤比较改进算法与传统SIFT算法所需的运行时间，结果见表1。

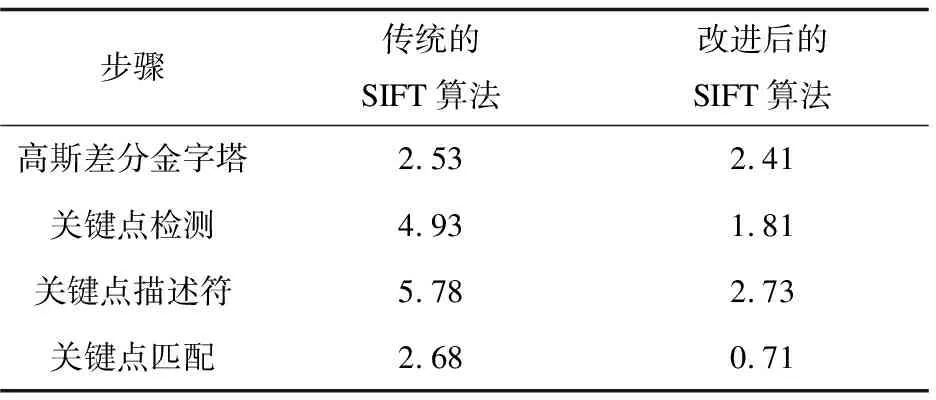
表1 比较两种算法中每一个步骤运行所需时间 s

针对图像发生旋转、几何变化以及光照变化的情况进行实验。比较不同情况下两种算法对图像的配准率影响，如表2所示。

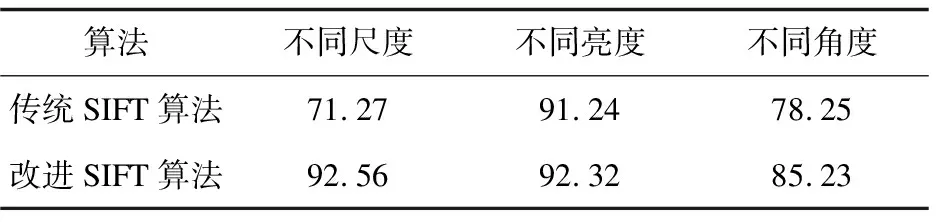
表2 比较两种算法的匹准效率 %

由表1和表2数据可知，虽然改进算法和传统SIFT算法得到的结果相近，但是改进的SIFT算法对图像关键点提取和配准所用时间明显小于前者，这大大提高了算法的实用性。

4 结束语

改进的SIFT算法采用积分滤波的方式构造不同尺度的图像。实验结果证明，改进的算法在保持原算法匹配精度的基础上，采用RANSAC算法剔除不稳定的关键点，提高了改进SIFT算法效率。采用双向配准，保留有效的关键点，缩短配准的时间，克服了传统SIFT算法计算过程复杂度高的问题且鲁棒性较好。但是，该算法提取待匹配图像上的关键点和度量其相似性的过程复杂、处理速度慢。因此，下一步工作是改进关键点的相似性度量方法和关键点的提取方法进而缩短工作时间。