基于Simhash改进的文本去重算法

张亚男，陈卫卫，付印金，徐 堃

(陆军工程大学 指挥控制工程学院，江苏 南京 210007)

0 引 言

进入大数据时代，数字化信息呈现爆炸式增长。伴随着云计算、大数据、物联网等信息技术的快速发展，数据量呈几何级增长，据IDC最新发布的报告预测，全球数据总量将从2016年的16.1 ZB增长到2025年的175 ZB[1]。随着全球生成和存储的数据越来越多，对存储容量的需求将继续以稳定的速度增长。但是无论是云存储系统，还是传统的数据存储系统，都存在大量的冗余数据，有的系统中数据重复率高达70%～90%[2]。越来越多的研究者开始关注解决数据冗余问题以缩减存储空间，重复数据删除技术应运而生。重复数据删除技术的核心思想是，只存储唯一的数据对象，对于其他重复数据则通过存储指针代替，指针指向该唯一数据对象。

当前流行的相似文本检测和去重算法主要有k-shingle[3]、Minhash[4]和Simhash[5]算法。Simhash是Google工程师Charikar等人提出的一种局部敏感哈希算法，用来解决亿万级别网页去重问题。Simhash算法较其他算法的优势是处理速度快，结果准确度高，被广泛应用于相似文本检测、冗余数据去重和数据异常检测等领域[6]。该文主要对Simhash算法在文本去重上的应用进行研究和改进，以进一步提高其检测重复文本的精确率。

1 相关研究

1.1 Simhash算法

传统的哈希算法能够对任意长度的输入数据进行计算，输出固定长度的哈希值。SHA-1、MD5等传统哈希算法，对输入数据非常敏感，只要有1 bit的差距都几乎不可能产生相同的哈希值，因此无法衡量文本的相似度。重复数据删除技术分为相同数据检测技术和相似数据检测技术两大类，传统的哈希算法对后者的效果并不理想[7]。Simhash的主要思想是降维，将高维的特征向量映射成低维的特征向量，通过这些向量的汉明距离(Hamming Distance)来判定文本的相似度。Simhash算法流程(如图1所示)大致如下：

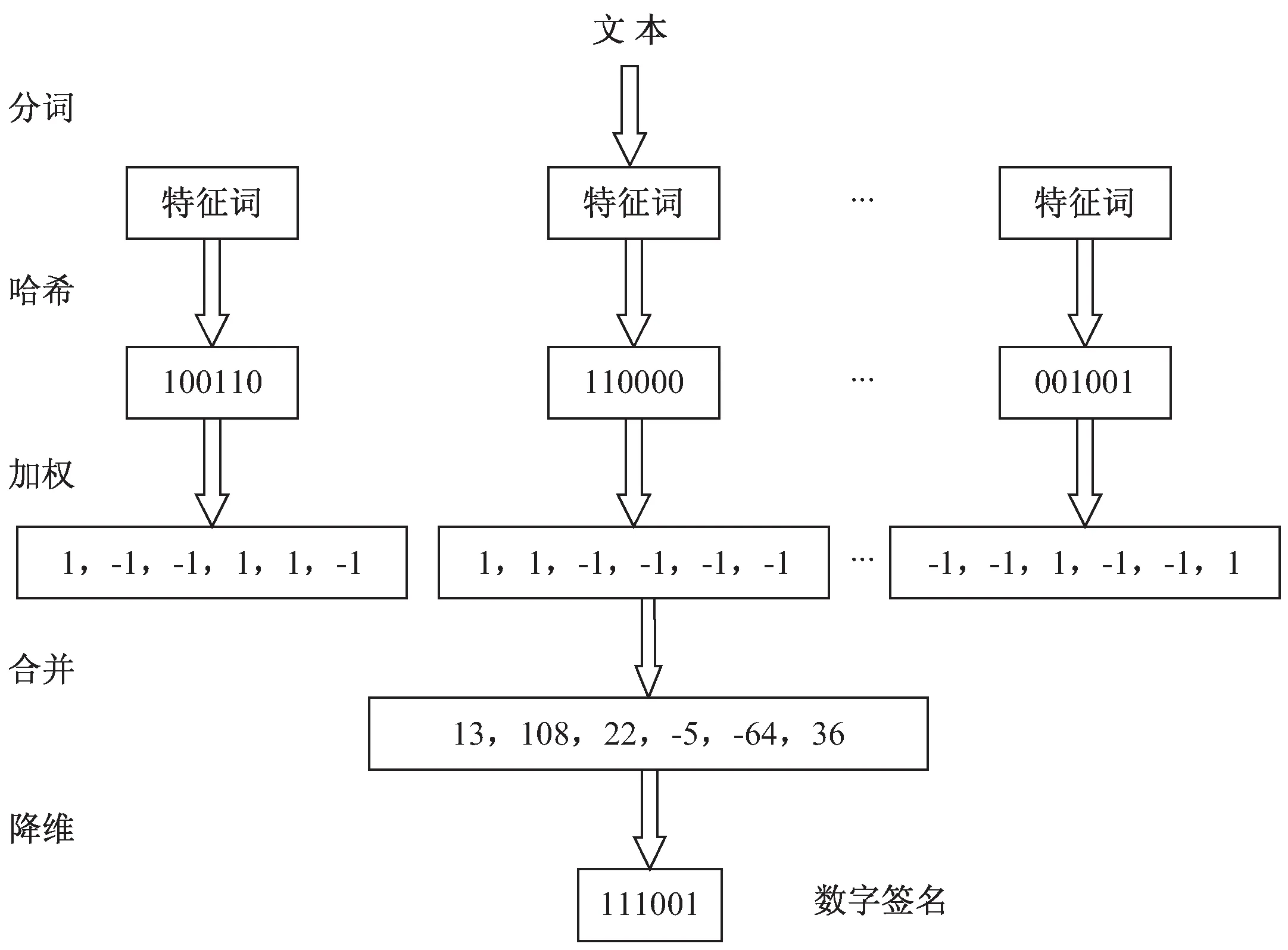
图1 Simhash算法流程

(1)分词。首先对文本进行分词，将文本转化为一组特征。然后，去除特殊符号、停用词等无关字词。

(2)哈希。使用同一哈希函数计算各个词的哈希值，分别得到它们对应的f位签名Sig。

(3)加权。为每个特征词赋予权重，对每个词的f位签名进行加权计算。在计算每个比特位时，遇到1则加上其权重值，遇到0则减去其权重值，得到每个词的加权特征值。

(4)合并。对文本内的每个加权特征值进行累加，得到一个f位向量V。

(5)降维。对向量V降维，对于每个比特位，如果大于0则将该比特位置为1，否则置为0。得到的结果作为文本的签名，记为S。

在计算文本间距离阶段，对不同文本的签名进行异或操作，逐位比较其签名值。如果该比特位上的值不同则记为1，否则为0，得到1的个数即为汉明距离的大小。汉明距离越大，代表两个文本相似度越低，反之则相似度越高。

1.2 当前研究现状

在大数据高性能存储应用领域，传统的Simhash算法已无法满足其需求。首先，特征词选取的精度不高，不能很好地体现文本特征。其次，对特征词权重的计算比较片面，导致准确率下降。针对上述问题，国内外研究者进行了进一步的研究与改进。

文献[8]针对特征词权重影响因素考虑不足的问题，在Simhash权重计算阶段，从词性、词长、标志词以及文档标题中是否含有特征词等几大方面对TF-IDF算法的权重计算进行改进，缺点是仅仅根据特征词的词性、长度和是否处于标题摘要等位置对权重进行优化，会导致部分权重过大。文献[9]将Simhash算法和GAN(Generative Adversarial Networks)网络进行结合用于恶意软件检测，通过转化为灰度图像提高恶意软件识别率和性能。文献[10]引入文档标签、摘要、关键词和参考文献等其他信息，从多个维度计算文本相似度，但是没有考虑词汇位置分布的影响因素。文献[11]提出的E-Simhash算法采用词频和熵加权的方式优化特征词权重计算，并针对Simhash算法无法体现特征词位置信息的问题，在特征词哈希时与其位置进行异或运算。但是在计算特征词签名时简单地将其哈希与所在位置进行异或运算，容易造成文本签名失真。例如在文本头仅仅添加一个文字就可能会导致所有特征词位置发生改变，造成文本签名值的显著改变。

以上对Simhash算法的改进主要存在两个问题。第一个问题是，在对特征词哈希加权时没有考虑特征词之间的关联性，例如待去重文本中可能存在几个大类，而属于某一类文本中的特征词具有很强的关联性，可能会同时出现。如果这些词同时占有较高权重，对于分类性能很好，但是却为差异检测带来了干扰。第二个问题是，不能很好地体现特征词位置分布信息。

2 改进的Simhash算法

针对以上提到的问题，对Simhash算法进行改进。传统的Simhash算法基于词袋模型，无法表征语序信息。但是仅考虑特征词出现的频率而不考虑语序特征，会影响结果的准确性。为了减少误判，该文将特征词的位置分布信息融入Simhash计算签名。为提高运算效率，选取权重前m的词语而非全部词语作为特征词。针对特征词的共现现象，根据Jaccard相似度对权重进行优化，降低相关度较高的特征词的权重，以提高检测精度。改进BDR算法用于反映特征词位置分布，使用随机函数将特征词所在位置映射到f维向量空间，对得到的特征向量累加得到均差向量，然后做降维处理作为位置特征值。取特征词哈希与位置特征值加权求和作为其特征向量，与优化后的特征词权重相乘，经合并降维后生成新的文本签名。最后，通过计算文本间的汉明距离来判断文本相似度，将A,B两个文本之间的相似度定义为：

(1)

其中，Ham(A,B)表示A,B两个文本的汉明距离，f表示文本签名值的比特位数。两个文本的距离越小，相似度越大。文献[12]的实验结果表明，对于64位的长文本签名，可以将汉明距离不大于3的两个文本判定为相似文本，同时保证较高的准确性。

2.1 特征词权重的改进

现有的基于Simhash改进算法主要使用TF-IDF算法为特征词赋权，在计算文本间相似性时没有考虑特征词之间的共现现象，而这与基于选择的特征降维模型前提条件“特征项之间相互独立”相矛盾[13]。文本集中的特征词可以分为三类[14]：第1类特征词在某一类文本中大量出现而在其他类文本里很少出现，第2类特征词常常在几个文本类别中出现而在其他类文本里很少出现，第3类特征词却在几乎所有文本类别中都出现。使用TF-IDF算法会对第3类特征词赋予极低的权重，对于前两类特征词通常会赋予较高权重。但是当前两类特征词出现共现现象时，由于都占据较高的权重，导致文本签名模糊，反而不利于文本去重。例如有以下文本：

①李白是唐代诗人

签名值：010011000101000100101101

②李白不是唐代诗人

签名值：010011000101000100111101

其中，词语“是”、“不是”就属于第3类，在几乎哪一类文本中都有出现，根据TF-IDF计算得到的权重很低。而“李白”、“唐代”、“诗人”这些词属于前两类，根据TF-IDF算法计算得到的权重较高。如果取权重前3的词语作为特征词，通过传统Simhash计算两个文本签名值距离为1，即使两个文本内容和含义有很大差异也会被判定为重复。而“李白”、“唐代”、“诗人”共现频率很高，由“李白”一词几乎可以代替其他词语，这样一来“是”、“不是”就成为影响文本签名值的特征词。

(1)TF-IDF算法。

在大数据高性能存储中，文本数量巨大，将每个文本分词后所得的词语数量会大大增加，为降低计算机运行的时空间复杂度，需要对分词结果进行筛选。TF-IDF算法是一种特征提取的方法，可以在尽量保证文本特征信息的同时缩减特征词的数量，达到降维目的。其一般表达形式为：

ωdt=tfdt×idf(Nnt)

(2)

其中，ωdt表示特征词t在文本d中的权重，tfdt表示特征词t在文本d中出现的频率，N表示文本集中文本的总数，idf(Nnt)表示逆文档频率，是对文本集中文本总数N和特征词t出现的文本数目n的比值取对数，用于权衡特征词重要性。在实际应用中，为减少文本长度影响，需要对特征词权重进行归一化处理。在改进的算法中，TFC[15]的应用最为广泛，其表达式可写作：

(3)

其中，mdt表示特征词t在文本d中出现的次数，Md表示文本d中的特征词总数，nt表示文本集中出现特征词t的文本数。

(2)Jaccard相似度。

Jaccard系数是一种二元数据对象的相似性度量方法，常用于比较有限样本集之间的相似性。其表达式为：

(4)

其中，J(x,y)表示二元对象x,y的相似度，f11表示x取1并且y取1的样本个数，f01表示x取0并且y取1的样本个数，f10表示x取1并且y取0的样本个数。在上式中，x取1表示样本中包含特征词x，反之则不包含，y同理。在实际应用中，特征词x,y即使同时出现在多个样本中，它们出现的次数也会呈现随机性。为了消除量纲的影响，对其做了以下改进：

(5)

其中，n表示同时包含特征词x,y的样本总数，xk表示第k个样本中特征词x出现的次数，yk表示第k个样本中特征词y出现的次数。

(3)相似度加权算法。

在计算特征词权重时，在TF-IDF基础上，根据Jaccard相似度对权重进行优化。算法简记为J-Tidf，由其计算得到的权重表达式为：

(6)

2.2 体现特征词位置信息的哈希签名

传统的Simhash算法基于词袋模型，无法表征特征词在文本中出现的位置。例如有以下文本：

①太阳队总决赛赢了雄鹿队

签名值：101110010101000100001100

②雄鹿队总决赛赢了太阳队

签名值：101110010101000100001100

即使两个文本的内容和含义大不相同，使用传统的Simhash算法也会得到完全相同的签名值。因此，该文针对文本词汇位置信息设计一套签名方案，以量化文本间的特征词分布差异。

2.2.1 BDR算法

BDR(Binary Dimension Reduction)是Rameshwar等人提出的一种稀疏二进制向量降维算法[16]，旨在通过维度压缩降低存储空间和提高计算效率，同时尽可能保留原始向量的特征。在词袋模型中，大多数单词很少出现在文本中。以Twitter为例，每条推文限制为140个字符，如果只考虑英文推文，由于英文词汇量为171 476个，每条推文都可以表示为171 476维度的稀疏二进制向量，其中1表示存在单词，0表示不存在。在BDR算法中，这种稀疏性是实现降维的前提[17]。BDR算法(如图2所示)分为以下几步：

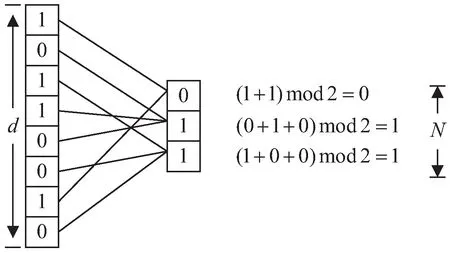
图2 BDR算法示例

①映射。对于由01组成的d维二进制向量u和N维向量v，选择一个随机函数，将向量u中的每个比特位映射到向量v上的每个位置。

②奇偶校验。对于映射到向量v上的每个比特位上的01求和，如果和是奇数则记为1，否则记为0。

压缩维度N的边界为ψ2log2n，与原始向量维度d无关。其中ψ表示数据稀疏性，即原始向量集合中出现1的数量最多的向量中1的个数，n表示待比较二进制向量个数。压缩后的数据继承了原始数据的内积，其汉明距离总是小于或等于原始数据的汉明距离，同时在Jaccard相似性计算上与Minhash保持几乎相同的准确性。

2.2.2 改进BDR算法用于表示特征词位置差异

BDR算法在保留数据对象内积的前提下有效实现了数据降维，但是随着待比较向量数目n的增加，文本长度增加导致稀疏性系数ψ变大，这使得压缩维度N不断增大。该文对BDR算法进行了改进，将其应用到特征词位置信息的降维表达上，在损失一定精度的情况下，可以大大降低压缩维度。改进后的算法简称PBDR，流程(如图3所示)如下：

图3 改进的BDR算法流程

①生成原始向量。对于每个特征词，统计其在文本中的位置，生成对应的d维二进制向量u，d表示文本词汇总数。对于每个比特位，如果该特征词在文本第p个位置出现，则向量u的第p位置为1，否则置为0。

②映射。选择一个随机函数，将向量u中的每个比特位映射到f维向量v。在计算向量v的每个位置时，将映射到该位的01值进行求和。

③求均差。对向量v每个位置，先求所有位置上数值的均值，然后将每个位置上的数值减去均值，得到该特征词的均差向量。

④降维。对特征词的均差向量降维，对于每个比特位，如果大于0则将该比特位置为1，否则置为0。得到反映特征词位置特征的签名，记为Sig'。

2.3 融合特征词词汇和位置信息的Simhash算法

改进后的算法(P-Simhash算法)主要针对传统Simhash算法为特征词赋权不够合理、没有体现文本特征词分布位置差异的缺点，在哈希、加权两个过程中做出改进。算法流程(如图4所示)如下：

(1)分词。使用Jieba分词工具对文本进行分词，去除特殊符号、停用词等无关字词。

(2)哈希。计算权重并按照权重大小选取前m个分词结果作为特征词，使用同一哈希函数计算各个词的哈希值，得到它们分别对应的f位签名Sig。

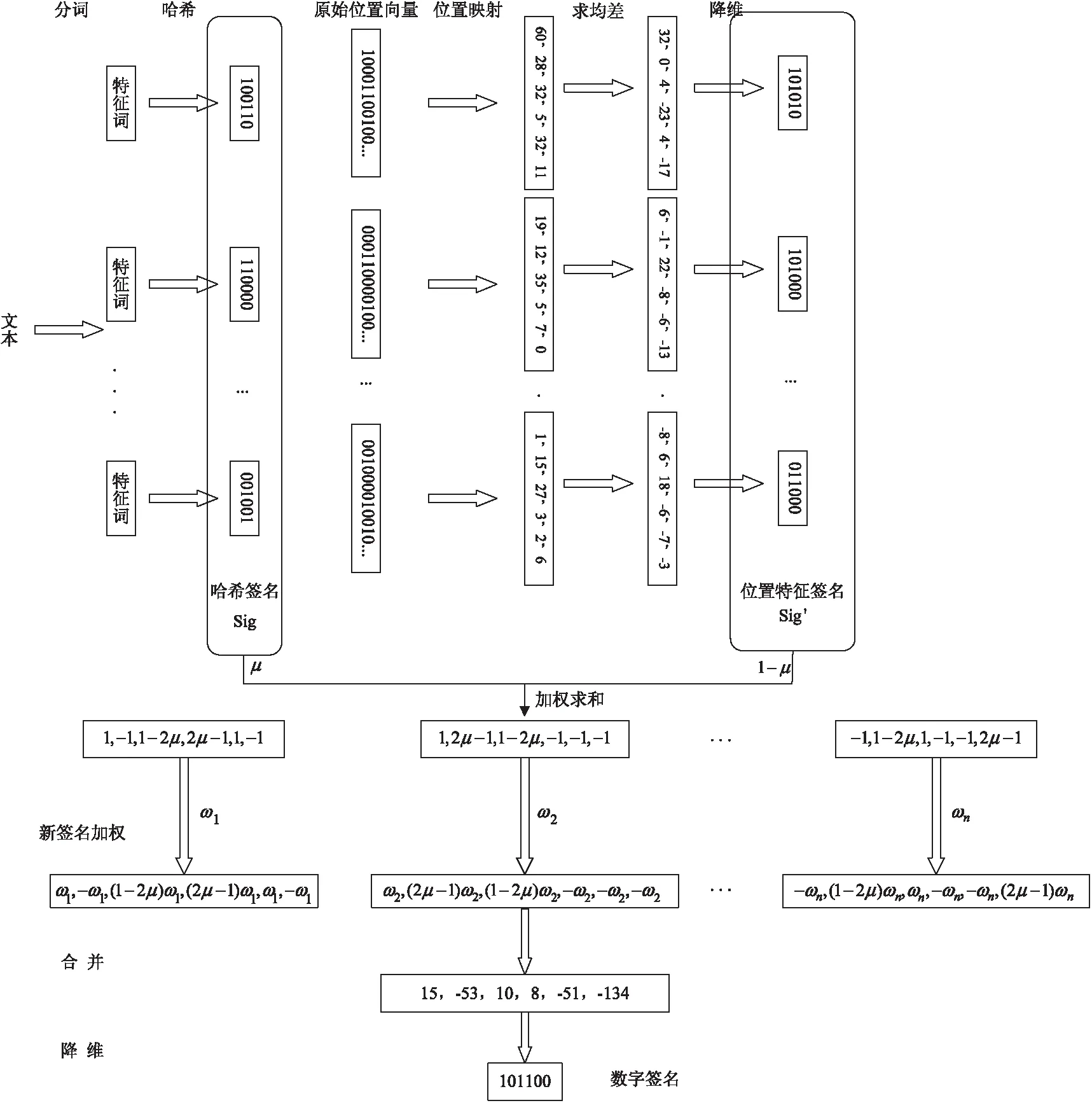
图4 P-Simhash算法流程

(3)位置特征转换。使用同一映射函数通过PBDR算法计算各个词对应的f位位置特征签名Sig'。

(4)签名加权合并。对于上两步得到的特征词的两种特征签名加权求和，得到其对应的特征向量SigFnl，计算公式为SigFnl=μ×Sig+(1-μ)×Sig'。在计算每一位时，如果遇到0则先将其置为-1然后再进行运算。

(5)二次加权。使用J-Tidf算法计算词的权重，对每个词的特征向量SigFnl进行加权计算。将特征向量对应的每一位上的数值乘以权重值，得到每个词的加权特征值。

(6)合并。对文本内的每个加权特征值进行累加，得到一个f位向量V。

(7)降维。对向量V降维，对于每个比特位，如果大于0则将该比特位置为1，否则置为0。得到的结果作为文本的签名，记为S。

3 实验及分析

为了检验提出的改进算法对重复文本的检测性能，选择搜狗新闻数据集作为实验数据，对原Simhash算法和改进后的Simhash算法进行对比。主要评估去重率、精确率、召回率和F1值[18]等指标，各指标的表达式如下：

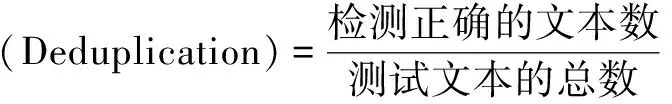
(7)

精确率(Precision)=

(8)

(9)

(10)

3.1 实验环境

实验代码采用Python语言编写，测试环境部署在Windows10操作系统上，硬件环境为Intel(R) Core(TM) i5-10200HCPU @2.40 GHz 处理器，8 GB内存容量，分词工具采用 Jieba3.0。

3.2 实验数据

数据集采用搜狗实验室中的全网新闻数据2012版，收录了来自若干新闻站点2012年6至7月期间国内、国际、体育、社会和娱乐等18个频道的新闻数据，有近10万条。首先剔除少于100个内容的新闻类别，然后再剔除其中字数小于800的新闻，随机选取4 246篇新闻进行后续实验。前文提及的E-Simhash算法在计算文本签名时也融入了特征词分布信息，因此该文也将重点与其进行实验比较。随机选取其中的2 831个样本作为训练集，用作计算特征词之间的Jaccard相似度，以优化其权重。在E-Simhash算法对比实验中，用作计算特征词的左右信息熵。将剩余的1 515个样本作为测试集，比较不同算法性能。

3.3 实验结果与分析

使用64位二进制01向量作为文本签名值，在计算签名值时μ值的选取待实验后给出。E-Simhash算法选取汉明距离为10并以此为基础开展实验，为了保证实验的客观性，汉明距离取10。

3.3.1μ的取值对去重率的影响

如2.3中所述，P-Simhash算法在第(4)步计算特征词对应的向量时，采用加权合并的方法得到融合位置分布信息的特征向量。对于任意比特位，若Sig和Sig'在该位上相同时μ值大小对结果无任何影响；当Sig和Sig'在该比特位上不同时，经加权计算得到的值域为|2μ-1|，μ值表征了特征词位置分布对签名的影响程度。μ取值越大，特征词位置分布不同带来的影响就越大，但是对于自然文本来说，大多数时候特征词位置的改变并不影响整个文本的语义。因此，当μ取值超过一定范围后，算法的去重率反而会下降。图5显示了μ在不同取值情况下，运行P-Simhash算法得到对应的去重率。实验结果表明，对于实验选取的搜狗新闻数据集，当μ取值在1.4到1.9之间时，P-Simhash的去重率达到比较高的程度。因此，进行后续的算法性能比较实验时，参数选择μ=1.5。

3.3.2 不同算法性能比较

P-Simhash在计算文本签名时融入了位置信息，计算的文本签名能够体现特征词位置分布差异的影响；同时在特征词哈希加权时降低了共现词的权重，避免了关联特征词具有较高权重导致签名模糊，因此相比其他算法拥有较高的精确率和召回率。如图6所示，P-Simhash算法在精确率上以0.946：0.803：0.909分别高于传统Simhash算法和E-Simhash算法，在召回率上以0.879：0.674：0.813分别高于传统Simhash算法和E-Simhash算法。F1值是评价去重算法性能的重要指标，在该指标上P-Simhash算法以0.911：0.732：0.858优于传统Simhash算法和E-Simhash算法。

图5 μ在不同取值下的去重率

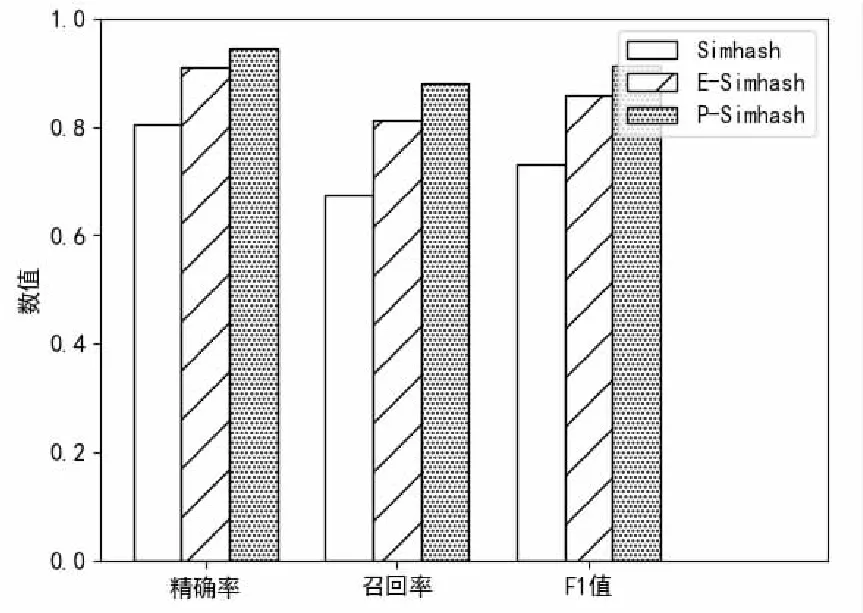
图6 算法性能对比

3.3.3 算法执行时间比较

P-Simhash算法在生成文本签名时加入了词汇位置特征计算，带来了一定的时间开销。为解决这一问题，该文采用前m个特征词而非全部特征词计算文本签名，因此可以节省大量的哈希运算时间。由图7可以看出，特征词权重几乎呈指数下降，当m大于20时，特征词的权重值很小，对生成签名值的影响也有限。因此，选择权重前20的特征词计算文本签名。

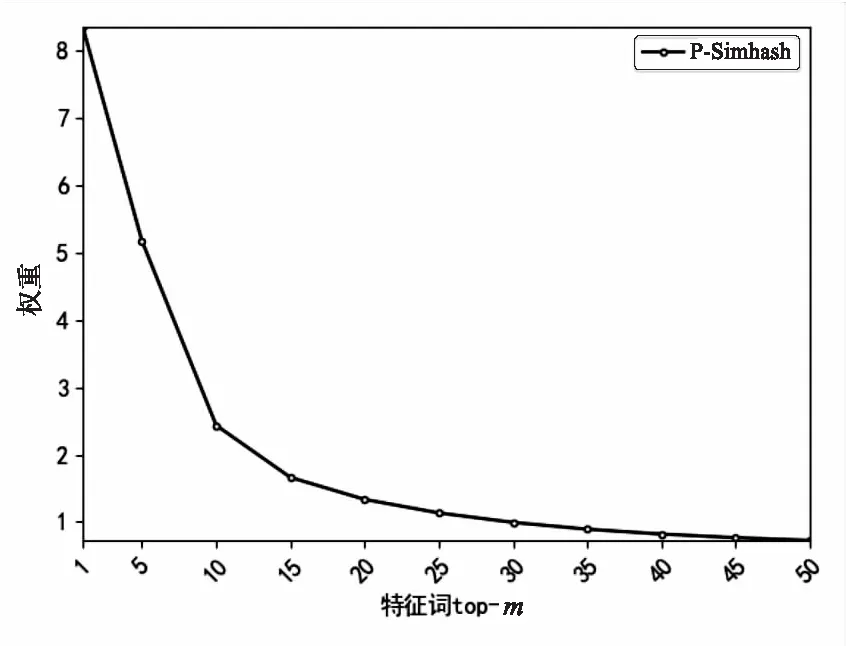
图7 前m个特征词的权重

为了比较不同算法的运行时间，将测试样本集通过裁剪拼接，调整每条新闻样本长度为1 000、2 000、3 000、4 000字，然后分别进行测试。实验结果如图8所示，随着文本长度不断增加，算法的执行时间也越来越长。P-Simhash算法由于在生成文本签名时加入了词汇位置特征计算，有一定的时间开销，但由于仅使用前20个特征词计算文本签名，节省了特征词哈希时间，因此P-Simhash算法执行时间与Simhash算法几乎相同。同时，由于无论文本长度变化始终选取前20个特征词计算文本签名，因此算法稳定性更好。而E-Simhash算法将全部特征词哈希与其每个位置分别进行异或操作，因此耗费时间更多。

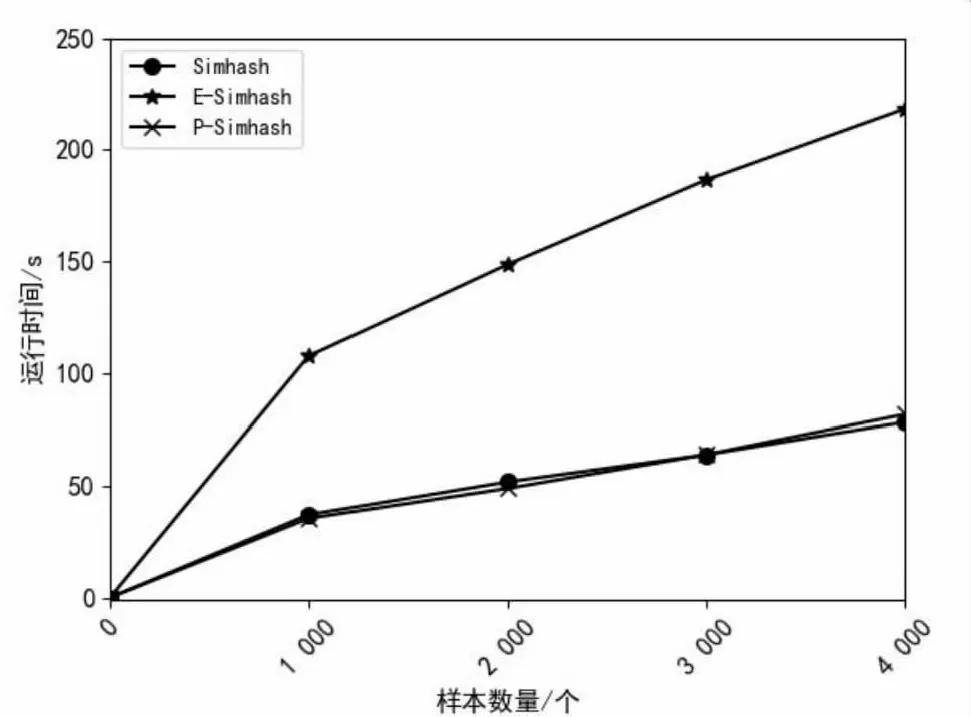
图8 算法执行时间对比

总结以上实验结果可以得出，P-Simhash以0.911：0.732将传统Simhash的去重效果提高了24.4%，而算法执行时间几乎相等。同时，在时间开销和去重性能上均明显优于E-Simhash算法。综合去重性能和算法执行效率，提出的P-Simhash算法较其他算法性能更好。

4 结束语

针对传统Simhash算法对重复文本检测精确度不高的问题，采用改进的Jaccard相似度计算方法计算特征词的关联度，适当降低共现词的权重，从而将注意力放在可能造成文本差异的部分。对于其无法体现特征词在文中分布的缺点，引入了二进制维度缩减算法，并在此基础上进行了改进，以便将特征词在文本中的位置分布信息映射到低维向量空间。设计了新的特征词签名，将词哈希与其位置信息结合在一起作为新的特征词签名。实验结果表明，提出的P-Simhash算法的去重性能较传统Simhash算法有明显提高。基于Simhash改进的中文文本去重算法普遍依赖ICTCLAS、Jieba等分词工具，如不能识别新词、分词不准确等会给相似度计算带来较大影响，在算法的分词阶段还有较大的改进空间。此外，上述算法直接将特征词进行哈希计算，缺乏衡量近似词的手段，两个同义词的哈希值很可能完全不同，可能导致两个相似文本相似度很低。下一步将针对词义的相似程度设计一套独特的词签名方案，以便更好地应用于相似文本检测工程。