基于改进TFIDF算法的邮件分类技术

陶 峰，汤 鲲，程 光

(1.武汉邮电科学研究院，湖北 武汉 430074；2.南京烽火星空通信发展有限公司，江苏 南京 210019；3.东南大学 计算机科学与工程学院，江苏 南京 210096)

0 引 言

中国互联网协会反垃圾邮件中心发表的《2014年第四季度中国反垃圾邮件状况调查报告》，根据调查结果估算，用户平均每周接收到的电子邮件数量为35.0封，平均每周接收到的垃圾邮件数量为14.3封，收到垃圾邮件的比例是41.0%。根据中国互联网协会反垃圾邮件中心的调查显示，有超过50%的用户因为反垃圾邮件功能弱而影响对电子邮件的满意程度。因此，如何实现对这类垃圾邮件的准确过滤成为近年来热门的研究课题。

垃圾邮件分类方法用的比较多的有朴素贝叶斯(Naive Bayes)[1-2]、神经网络[3]、K-近邻[4]、支持向量机(SVM)[5-6]等。由于邮件分类算法都是建立在特征项提取基础上的，因此特征项提取直接影响着邮件的分类效果。

TFIDF[7-10]是广泛使用的权值计算方法，用术语频率乘以逆文档来表示特征项的权值。近年来，不少学者将TFIDF算法用于特征提取，并在实验中取得了较好的效果。目前，在邮件分类中常用的特征提取方法有：信息增益[11-12]、互信息[13]、期望交叉熵、文本证据权、CHI统计[14]以及TFIDF算法。TFIDF因其便于理解、操作简单、时间复杂度低等优点而应用广泛，但是仍然存在很多不足。该方法只考虑了特征词文档的绝对数量和特征词在某类邮件中的词频，没有考虑到特征词在类中的分布情况和特征词在其他类邮件中的词频，高估了低频词的作用并低估了高频词的作用。文中将对TFIDF进行一定的修改和优化，以克服传统TFIDF的缺陷。

1 特征提取算法及其改进

1.1 CHI统计算法

CHI统计算法是使用统计的方法计算特征词t与邮件类别d的关联程度。特征词t与邮件类别d的相关度表示如下：

(1)

其中，N表示邮件总数量；A表示邮件类别d中包含特征词t的邮件数量；B表示包含特征词t但是不属于邮件类别d的邮件数量；C表示邮件类别d中不包含特征词t的邮件数量；D表示不属于邮件类别d也不包含特征词t的邮件数量。

1.2 传统的TFIDF算法

TFIDF的主要思想是：如果一个特征词在一类邮件中出现的频率TF较高，并在其他类邮件中出现频率较少，则认为这个特征词具有较强的类别区分能力，适合用于对邮件分类。TF是词频，表示特征项在一类邮件中出现的频率。IDF是逆文档频率，是特征在文本空间中分布情况的量化，常用的计算方法是IDF=log(N/n),N表示总的邮件数量，n表示出现特征向量的邮件数量。TFIDF是结合词频和逆文档频率两种属性而得到的计算方法，具体计算公式如下：

W(d,t)=tf(d,t)×log(N/n)

(2)

其中，W(d,t)表示特征t在邮件类别d(垃圾邮件或者正常邮件)中的权重。

1.3 TFIDF算法存在的问题

TFIDF算法是将邮件集作为一个整体来进行处理，并没有考虑到特征词的分布问题，明显存在以下三点不足：

(1)考虑到特征词在类内分布的情况：如果一个特征词在某一类邮件中均匀分布，则说明这个特征词能很好地区分该类别，分类能力较强，该特征词应该被赋予较高的权值。相反，如果一个特征词只在某一类邮件中的几封邮件中出现，则说明这个特征词不能很好地代表该类邮件，应该赋予较低的权值。对此，传统的TFIDF算法并不能很好地处理。

(2)TFIDF算法并没有考虑到特征词在类间的分布情况，TFIDF算法只考虑到特征项在某一类邮件中出现的频率情况。如果特征词在一类邮件中出现的频率很高，但是在另一类邮件中出现的频率很低，这样的特征词应该被赋予很高的权值。相反，如果特征词在某一类邮件中出现的频率很高，但是在另一类邮件中出现的频率也很高，这样的特征词代表性很差，应该赋予较低的权值。对此也需要进行一定的改进。

(3)IDF的主要思想是：如果包含特征词t的文档越少，即n越小，IDF越大，说明特征词t的区分能力越好。如果特征词在某一类邮件中大量出现，n也会很大，按照IDF公式得到的IDF的值会很小，说明这个特征词区分能力不强。实际上特征词在某一类中大量出现，说明该特征词能够很好地代表这类邮件，这样的特征词应该被赋予较高的权值。相反，如果特征词比较均匀地分布在垃圾邮件集和正常邮件集中，这样的特征词对分类的贡献较小，即使其中包含特征词t的邮件数量n较小，也应该赋予较小的权值，但是IDF却赋予较大的值，显然不合理。

如表1所示，假设有5封正常邮件和5封垃圾邮件，若只考虑3个特征词，分别用t1、t2、t3表示，di(i=1,2,…,5)表示垃圾邮件，ni(i=1,2,…,5)表示正常邮件。

表1 特征词分布表

从表1可以看出，特征词t1在垃圾邮件中均匀分布，说明特征词对垃圾邮件的分类能力较强。t1特征词没有在正常邮件中出现，说明对正常邮件没有分类能力。特征词t2在垃圾邮件中出现频率很高，但是集中在个别邮件中，说明特征词t2的分类能力较弱。t3在垃圾邮件和正常邮件集中均匀分布，几乎没有分类能力。

根据传统的TFIDF算法分别计算特征词t1、t2、t3的权值大小，结果见表2。

表2 传统TFIDF权值计算结果

从表2可以看出，特征词t1在垃圾邮件类别中的权重为10.4，而特征词t2和t3在垃圾邮件类别中的权重分别为34.5和15.3。当邮件集中出现特征词t1和t2的频率相同时，特征词的权重由IDF确定，但是仅仅考虑特征词出现的文档数量显然是不合理的。特征词t3在垃圾邮件和正常邮件之间分布均匀，说明该特征词不具备分类能力，结果却被赋予较高的权值。因此可以看出仅仅使用传统的TFIDF算法，不能选择出更有代表性的特征词。

1.4 TFIDF算法的改进

(1)针对传统的TFIDF没有考虑到特征词在邮件类中的分布情况进行改进。假设垃圾邮件(或者正常邮件)中第i封邮件中出现特征词t的频率为ni。

(3)

其中，TF(d,t)表示改进后的TF算法，表示特征项t在邮件类别d中出现的频率；a(a≥1)是常数，可以通过实验来确定最佳值。

f(x)=log(x+1)2与f(x)=x的函数图如图1所示。

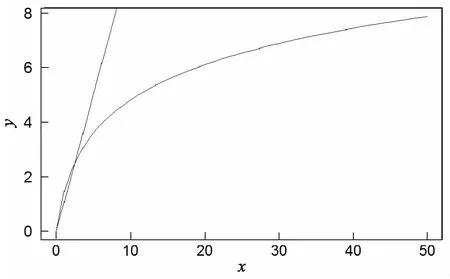
图1 函数图

由图1可知，两个函数都是递增函数，即当一封邮件出现的次数越来越大时，TF的叠加也随之增加。随着x的增大，f(x)=log(x+1)2的增大会变得平缓，当特征词在某一类邮件中没有出现时，TF=0。假设a=2，当一封邮件某一特征词都只出现1次的时候，TF叠加log(22)=1.3863；当一封邮件某一特征词出现9次，TF叠加log(102)=4.6052；当一封邮件某一特征词出现99次，TF叠加log(1002)=9.2103。可以看出，改进后的TF算法不仅很好地抑制了某个特征词在特例邮件中大量出现的情况，又能体现出特征词在邮件中大量出现比在邮件中只出现一次更重要。

(2)针对传统的TFIDF算法仅仅考虑到特征词在一类特征词中的出现情况对其进行改进。当特征词在不同类别的邮件集中出现的频率相差较小时，这样的特征词应该被赋予较小的权值，相反当特征词在不同类别的邮件集中出现的频率相差较大时，应该被赋予较大的权值。在这里引用频率差的概念：

(4)

通过使用频率差来反映特征词分别在正常邮件和垃圾邮件中的差异，对于在两类邮件出现频率差不多的特征词赋予较小的权值，这也符合需要的特征词的要求，选择出更加有区分度的特征词。

(3)针对IDF的不足提出改进，当某一类邮件中出现特征词t的邮件数量较大，在另一类邮件中出现的邮件数量较小时，说明特征词t有很好的区分能力。改进后的IDF算法如下：

(5)

其中，IDF(d,t)表示特征词t在邮件类别d中的IDF值；N表示总的邮件数量；A表示邮件类别d中包含特征词t的邮件数量；B表示包含特征词t但是不属于邮件类别d的邮件数量；C表示邮件类别d中不包含特征词t的邮件数量；D表示不属于邮件类别d也不包含特征词t的邮件数量。

假设邮件总数量为N，邮件类别d的邮件数量为Nd，那么不属于邮件类别d的邮件数量为N-Nd。可以得到:

A+C=Nd

(6)

B+D=N-Nd

(7)

则改进后IDF算法的变形公式为：

(8)

其中，N、Nd是已知值，且A与B分别表示两个类别的邮件集中出现特征词t的邮件数量，是互不相关的。因此可以看出，IDF随着A的增大而增大，IDF随着B的增大而减小。改进后的IDF算法能够很好地体现这个思想：特征词在某一类邮件中出现越多，在另一类邮件中出现越少，这个特征词应该赋予更高的权值。

结合上面对TFIDF算法的改进，得到最终的TFIDF权值计算公式：

W(d,t)=F(d,t)×IDF(d,t)

(9)

计算特征词t在垃圾邮件中的TFIDF值时，先对特征词t在垃圾邮件中的TF与特征词t在正常邮件中的TF进行相减，再与IDF相乘得到。

2 实验与分析

2.1 实验数据

从CCERT提供的中文邮件中随机抽出5000封正常邮件和5000封垃圾邮件作为训练集，500封正常邮件和500封垃圾邮件作为测试集。将其等量分为5份，每份训练集包含2000封邮件(1000封正常邮件，1000封垃圾邮件)，每份测试集包含200封邮件(100封正常邮件，100封垃圾邮件)。

2.2 分类器

文中使用了朴素贝叶斯算法[15-16]，根据样本训练构建的特征库通过贝叶斯公式计算出待分类邮件属于垃圾邮件和正常邮件的概率。同时比较属于正常邮件的概率和属于垃圾邮件的概率，来判断邮件属于哪一种类别，这样能很好地提高分类的准确率。具体公式如下：

P(d|e)=[p1×p2×…×pn]/[p1×

p2×…×pn+(1-p1)×

(1-p2)×…×(1-pn)]

(10)

其中，P(d|e)表示待分类的邮件e属于邮件类别d的概率；Pi表示特征词ti在邮件类别d中出现的概率，通过训练样本得到。

最终通过比较P(normal|e)与P(trash|e)的大小，来确定待分类邮件e属于正常邮件还是垃圾邮件。

2.3 实验评价体系

借助文本分类和信息检索领域的技术指标来评价邮件分类算法的性能。评价体系见表3。

表3 评价体系

召回率(recall)：也称查全率，即垃圾邮件的查出率，该指标系数越高，说明找回漏掉的垃圾邮件能力越强，计算公式如下：

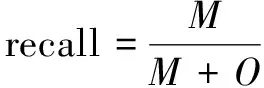
(11)

正确率(precision)：也称查准率，即垃圾邮件的查对率，该指标系数越大，说明合法邮件被误判的风险越小，计算公式如下：

(12)

F值：是召回率R和正确率P的调和平均值，是召回率和正确率的综合评判标准，公式如下：

(13)

精确率(accuracy)：对所有邮件的判对率，表明正确判定全部邮件的能力，公式如下：

(14)

其中，X表示测试邮件总的数量。

2.4 实验结果

分别使用传统的TFIDF算法和改进后的TFIDF算法对五组样本集进行实验，结果如表4～6所示。

表4 CHI统计算法特征提取实验结果

表5 传统的TFIDF算法特征提取实验结果

表6 改进后的TFIDF算法特征提取实验结果

结合表4和表5，可以看出传统的TFIDF算法在正确率、F值、精确率上都要高于CHI统计方法，召回率略低于CHI统计方法。说明TFIDF算法适合于进行特征提取。

结合表4、表5和表6，可以看出使用改进后的TFIDF算法，垃圾邮件分类效果比使用CHI统计算法和传统TFIDF算法的分类效果要好。召回率、正确率、F值、精确率都有一定的提高，这也证明了改进后的TFIDF算法更有效。

3 结束语

TFIDF特征权值计算方法在垃圾邮件过滤中被大量使用，但是仍然存在一些不足之处。文中对其没有考虑到特征词在类中分布情况、没有考虑到特征词在另一类的出现频率、低估了频繁出现的特征词的权值并高估了出现频率低的特征词的权值这三方面进行改进。以朴素贝叶斯算法作为分类器，分别计算测试邮件是正常邮件和垃圾邮件的概率。最终以召回率、正确率、F值、精确率作为评估指标，将改进后的TFIDF和CHI统计特征提取、传统的TFIDF进行比较。通过实验数据进行分析，说明改进后的TFIDF算法是有效的。