求解柔性作业车间调度问题的混合遗传算法
李雪花,高全力,赵 辉,杨 昊,金 帅,徐国梁
(1.西安工程大学 计算机科学学院,陕西 西安 710048;2.山东如意毛纺服装集团股份有限公司,山东 济宁 272000;3.山东如意恒成产研新材料科技有限公司,山东 济宁 272000)
0 引 言
柔性作业车间调度问题(Flexible Job-Shop Scheduling Problem,FJSP)是离散制造业、流程工业等实际生产中的核心问题。FJSP问题是JSP(Job-shop Scheduling Problem)问题的扩展,包括复杂的约束条件,包括对每个工序加工时间,工序的加工顺序,以及加工设备的约束。因此,FJSP是一个典型的NP难问题。解决FJSP问题的常见方法是群智能算法,一些最常用的算法包括遗传算法、粒子群算法、鱼群算法等。
遗传算法(Genetic Algorithm,GA)是一种通过模拟自然进化机制来搜寻最优解的全局优化算法[1],全局搜索能力强,具有可扩展性,容易与其他算法结合,但其局部搜索能力较差,容易“早熟”收敛,且对初始种群的选择有一定的依赖性[2]。近些年来一些学者通过融合遗传算法与其他算法来改善其鲁棒性,实现性能提升。陶泽等融合了遗传算法和模拟退火算法,从而提高了种群的收敛速度并防止种群陷入局部最优[3]。LI等提出一种将禁忌搜索算法与遗传算法有效结合的禁忌混合遗传算法,增强了遗传算法局部搜索能力,但计算成本较高[4]。杨振泰等提出了一种结合powell搜索法的遗传算法,改善了GA算法在迭代过程中产生比可行解的情况[5]。贾培豪等融合鲸鱼算法和遗传算法,改进传统遗传算法后期的局部搜索能力,提高算法求解质量[6]。综上所述,标准的遗传算法融合其他算法是求解FJSP问题的趋势所在。该文提出一种混合遗传算法,在遗传算法的基础上,在初始种群生成时采用混沌理论产生分布均匀的随机数提高初始种群在解空间分布的均匀性,且根据FJSP问题特性改进交叉、变异规则,将表现优异的个体加入优良种子库进行保护。并采用混合蛙跳算法对优良种子库进行局部搜索寻优,将得到的更优解与下轮个体交叉迭代,提高局部搜索能力,改善传统遗传算法“早熟”问题。通过对mk01~mk10标准算例进行仿真实验,验证了该算法的有效性与可行性。
1 FJSP概述
1.1 问题描述
FJSP问题一般包含n个工件,Job={J1,J2,…,Jn},每个工件都有一道或多道加工工序,某一工序可以在机器集M中,M={M1,M2,…,Mn},任意选择一台进行生产加工,其加工时间与选择的机器相关。处理FJSP问题时需要考虑工序的加工顺序、加工机器和最大完工时间。该文以“最小化最大完工时间”作为优化目标。
1.2 数学模型
为了便于解释FJSP的数学模型,相关参数(见表1)如下:
优化目标:
(1)
约束条件:
(1)每道工序的加工时间约束:
Si,j+pi,j,k≤Ei,j
(2)
asi,j≥Ei,j-1
(3)
Ej,nj≤Cmax
(4)
(2)同一工件的相邻两道工序的加工时间约束:
Ei,j≤Si,j+1j+1≤ni
(5)
(Si,j+pi,j,.k)bi,j,p,q≤Sp,q,i≠p或j≠q
(6)
(3)某工件的某工序选择的加工机器约束:
(7)
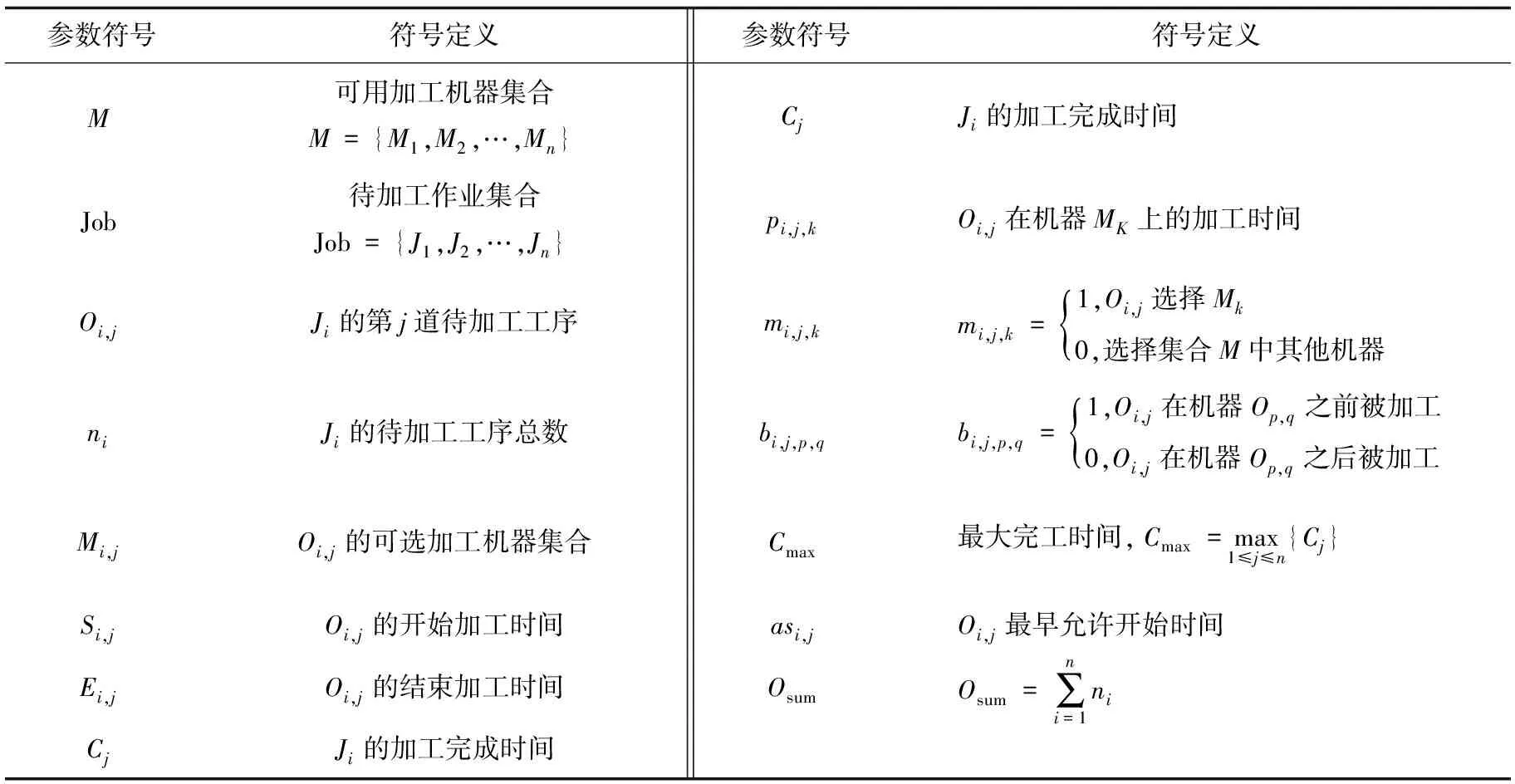
表1 FJSP相关参数符号定义
2 混合蛙跳算法
SFLA(Shuffled Frog Leaping Algorithm)[7]是根据青蛙种群在石块上觅食时的分布变化而提出的算法。青蛙所在的池塘中有若干石块,青蛙们会按照特定规则被分配到石块相应位置上。每个青蛙的位置代表了问题的一个可行解。在每一代中,每个石块上处于最差位置的青蛙会跳动,该青蛙首先会朝向位于同一石块上最优位置的青蛙跳动,若跳动后的新位置比原来位置差则向着全局最优位置跳动,若该位置仍旧比原位置差则再在解空间内随机跳动一次,可见可以跳动的青蛙最少跳动一次,最多跳动三次。当每个石块上的青蛙都跳动后,将各个石块上的青蛙合并,并重新合并然后分组,重复上述跳动过程,直到满足终止条件。流程如图1所示。
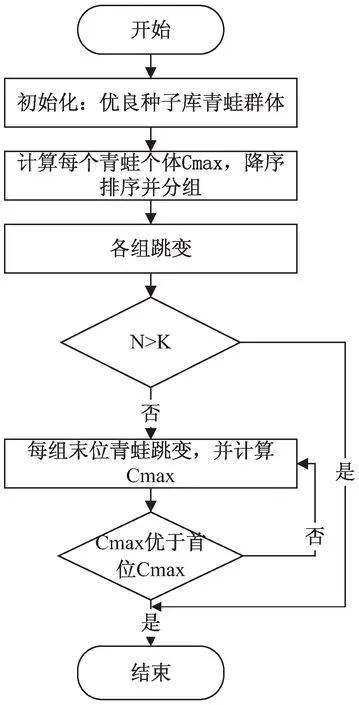
图1 混合蛙跳算法过程
详细步骤如下:
Step1:将优良种子库中的种群作为青蛙种群分为K个组,位列第1的青蛙被分配给第1组,位列第2的青蛙分配给第2组,以次类推,直至将所有青蛙分别分配到K个组中,每个组中包含N/K个青蛙。
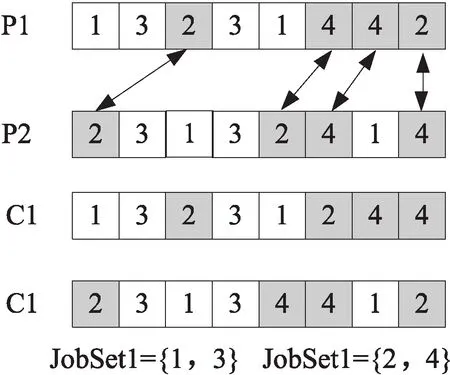
Step2:对每组执行搜索过程。每组中排在最后位置的青蛙R向这个组中位置第一的青蛙F跳变,跳变规则为:Oi,j为R青蛙的OS部分与F青蛙的OS部分相异的基因位表示的工序,将此工序当前安排的加工机器替换为此工序可选机器中时间加工最短的机器。若有多个相异工序,则全部替换。如图2,F青蛙与R青蛙第三个位置的基因不同,此基因代表的工序是O3,1,因此根据规则将R青蛙MS部分代表O3,1的加工机器3替换为时间更短的加工机器2。然后计算R青蛙的适应度值,若优于位置第一的染色体,则替换其位置,否则继续变换。
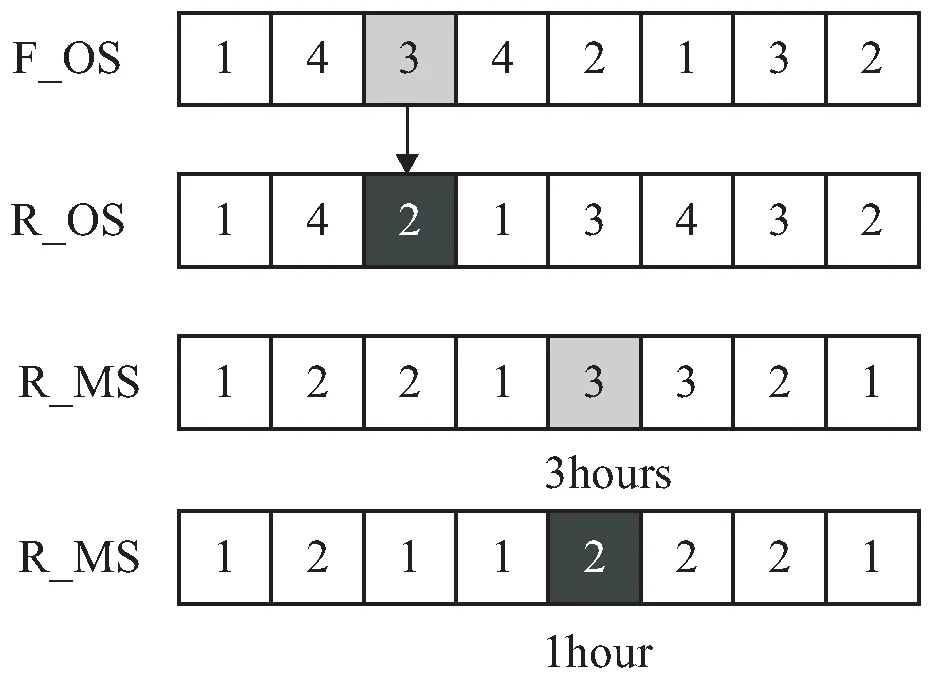
图2 跳变规则
Step3:判断是否满足停止条件,如满足停止条件则停止。如不满足则跳转Step2执行。为防止将解劣化,若R青蛙没有跳动则此青蛙保持原来的值。
3 算法的总体过程
整体算法流程如图3所示。
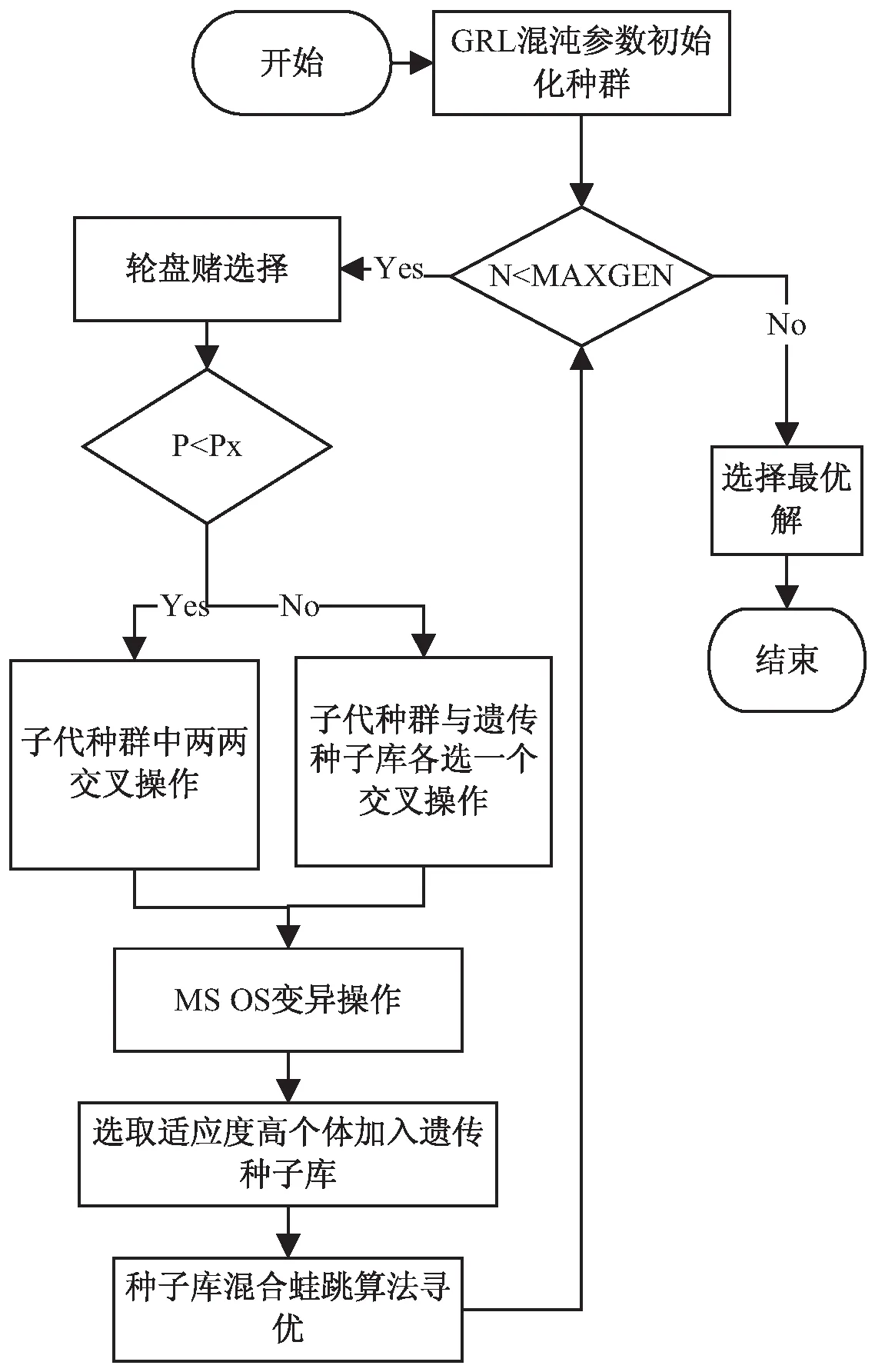
图3 算法整体流程
算法具体步骤如下:
Step1:采用1.2节提出的混沌随机数发生器生成随机数,并结合GLR机器选择法[8],其中GS:LS:RS=0.6:0.3:0.1,从而生成分布均匀且个体适应度较好的初始种群,个体适应度值为Fi=1/Cmax。
Step2:若迭代次数大于MAXGEN,则找到当前最优解作为问题的最终解;否则,执行Step3。
Step3:采用轮盘赌选择法从种群中选择子代种群。
Step4:以概率pc在Step3选择的子代种群中选择进行交叉操作的部分个体,再以交叉方式选择概率px选择采取何种交叉方式。
Step5:根据变异概率pm,从交叉后的种群中选取需要变异操作的个体,进行变异操作。
Step6:选取适应度值高的个体加入遗传优良种子库。
Step7:执行混合蛙跳算法,在遗传优良种子库中进行局部搜索寻优,更新优良种子库。
Step8:跳转执行Step2。
3.1 染色体编码方案
文中染色体编码方案采用MS-OS编码方案[6],如图4所示,包括四个工件,每个工件包括两道工序。染色体编码分成两部分:OS(Operations Sequencing)部分与MS(Machines Selection)部分。OS部分有Osum位,数字i出现的第j次,代表工序Oi,j。例如图4中OS部分的第一个“1”代表O1,1,即第一个工件的第一道工序,第二个1代表O1,2,即第一个工件的第二道工序。

图4 FJSP染色体编码示例图
MS部分也有Osum位,按工件顺序排列,第i个工件领域的第j位置数字m,表示Oi,j选择其可选加工机器的第m个机器进行加工。如图4中MS部分有四个工件,每个工件有两道工序,J1领域的第一位数字“1”,代表O1,1工序选择在O1,1的可选加工机器集合Mi,j中的第1个机器上;J1领域的第二位数字“2”,代表O1,2工序需要安排在O1,2的可选加工机器集合Mi,j中的第1个机器上。解码时,当工序Oi,j被安排在机器k,即mi,j,k=1,检查机器k所有空闲时区[ts,te],若存在区间满足max(asi,j,ts)+pi,j,k≤te,则将工序Oi,j插入到区间[ts,te]中,且Si,j=ts。若不存在则放置到机器加工队列最后。
3.2 种群初始化
基于混沌原理所产生的随机数在限定空间内具有更好的遍历性和随机性,并且具有产生速度快、易于实现等特点。将其应用在遗传算法中,从而提高初始种群在解空间分布的均匀性及降低算法陷入局部最优解的可能性。所以文中所有的随机参数均为提出的结合Tent映射与Logistic映射的混沌随机数发生器生成。
Tent混沌映射生成器[9]的迭代公式如下:
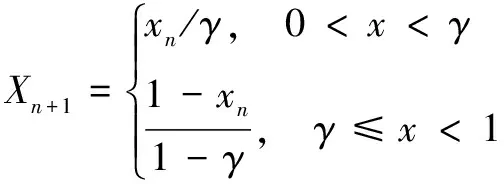
(8)
Tent映射是在区间[0,1]之间的两个分段的线性迭代,包含一个参数,其中γ为常数,γ∈[0,1]。序列的计算过程为:在区间(0,1)中任意选择一个初始迭代点,迭代计算Xn+1即可得到一个该区间上的混沌映射。Logistic混沌映射的迭代公式如下[10]:
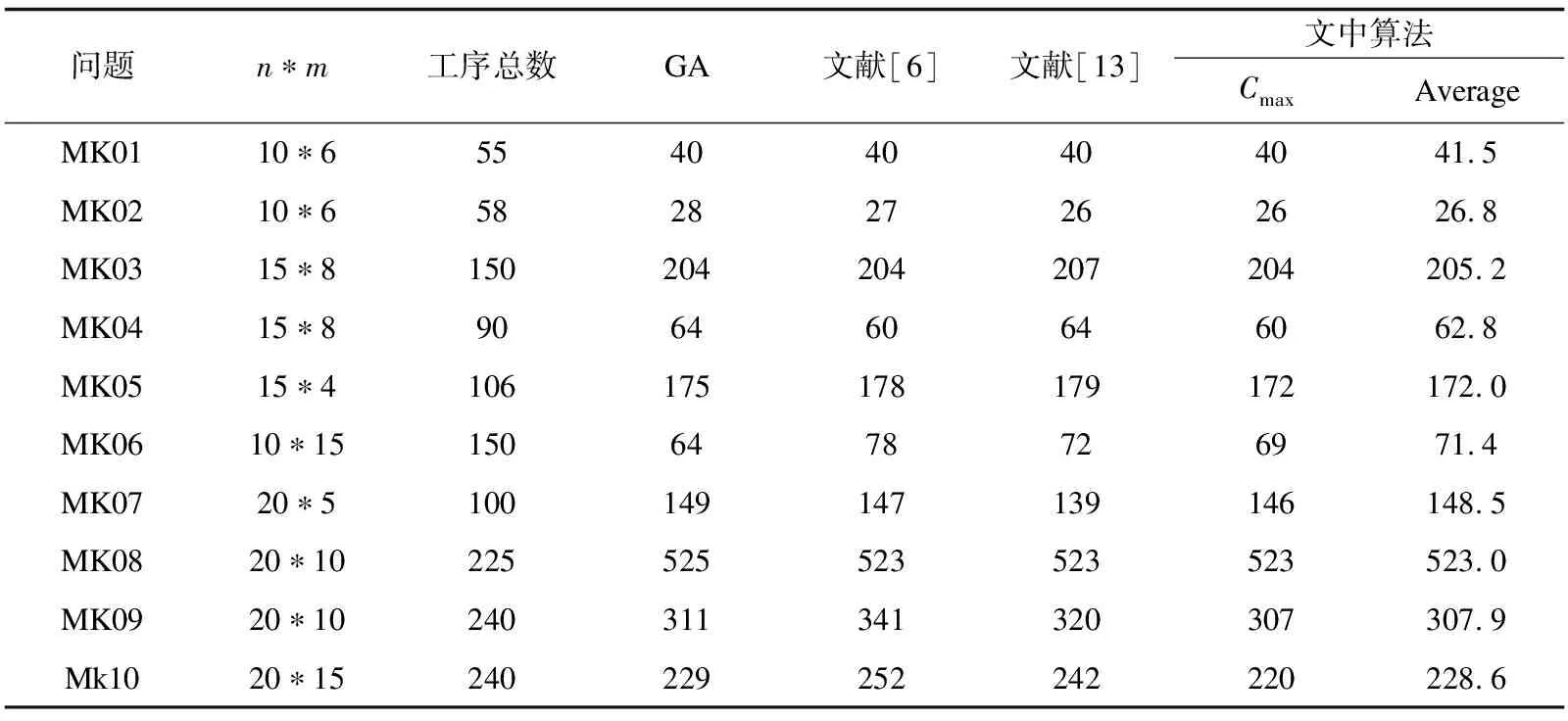
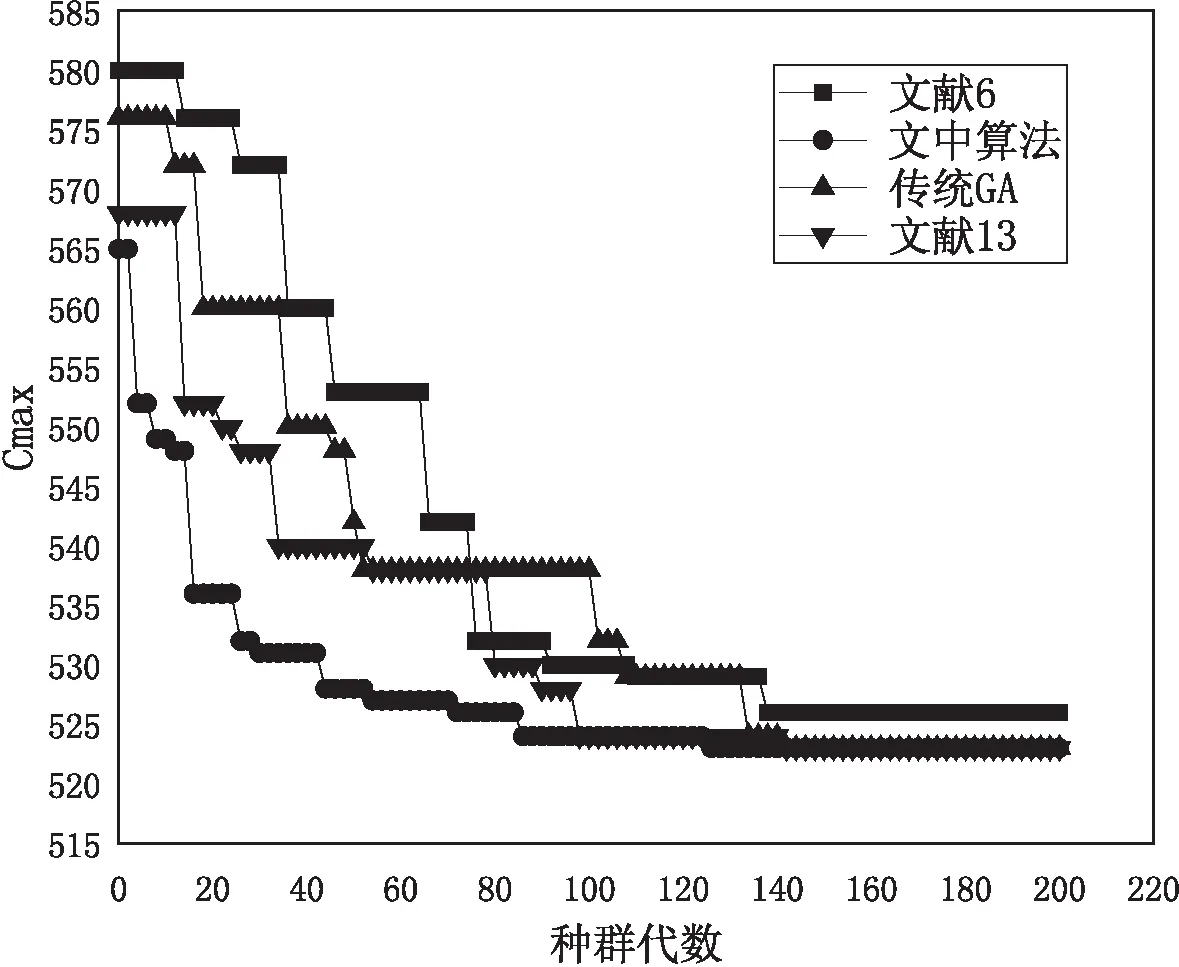
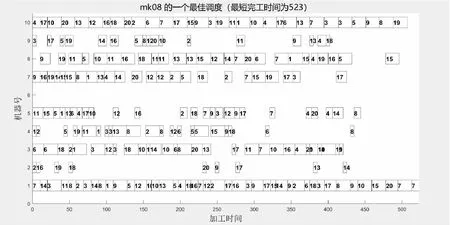
Xn+1=f(xn)=α×xn×(1-xn),0 (9) 其中,α为Logistic参数,当3.569 945 6<α≤4时,迭代生成的值非周期,有良好的随机性。n为其迭代次数。 该文将Logistic结合Tent得到随机数生成器,取α=4,γ=0.5。其迭代公式如下: (10) 采用轮盘赌选择法从种群中选择子代种群[8],个体选中的概率与其适应度函数值成正比,即适应度越大被选择进行交叉操作的概率Pi越大。Pi计算方式如下: (11) 机器选择MS部分采用均匀交叉方式交叉,即依次扫描每个基因,以概率PS与对位基因进行交叉操作,PS为0.5,如混沌随机数大于PS,则与对位基因互换,否则不互换。 OS交叉操作选择改进SEX[8](子路径交交换交叉)交叉方式,如图5所示。随机划分工件为两个非空集合,随机选择其中一个集合,在两个父代染色体中选中此集合基因,然后顺序交换两个父代其余位置基因,得到两个子代。 图5 子路径交交换交叉示意图 (12) 遗传算法中交叉算子全部来自于当前种群,即有可能当前种群经过选择的优秀个体在交叉时被破坏了。为了解决这一问题,该文采用优良遗传库策略,将当前种群产生的优良个体加入优良种子库,并利用混合蛙跳算法(SFLA)针对OS序列对应的MS序列寻优,从而得到更优的目标函数,得到的更优解供下一轮迭代的交叉操作,从而保留优秀个体并有目的性地对MS序列进行优化。 为检验该算法的有效性与可行性,通过Brandimarte(mk01~mk10)[12]算例对算法进行测试。算法实现采用JAVA语言,实验环境为windows10系统,处理器为Intel i7 10750H 六核CPU、主频为2.60 GHz、内存16 GB。种群规模Size=200,最大迭代次数 MAXGEN=200;交叉概率pc=0.8,交叉方式选择概率px=0.3,变异概率pm=0.05;优良种子库的容量Cseed为种群规模的10%。为充分体现混合蛙跳算法寻优能力,其分组个数K=10。 将mk01~mk10分别计算10次,记录最优值及平均值,将其与文献[6,13]提出的算法结果及一般GA算法结果进行比较,如表2所示,可以看出除了mk06与mk07算例,其他均得到了所对比算法中的最优解,验证了文中算法的有效性。 表2 各算法对MK08算例求解结果对比分析 以20*10即20个工件10台机器的mk08算例为例,算例描述如表2所示。图6对比了传统GA、文献[6,13]所提算法的性能。可以看出由于文中算法采用了混沌理论使初始解在解空间分布更均匀,所以初始种群的最优值优于传统GA及文献[6,13]所提算法,且由于改进了交叉与变异策略及采用了保优策略,算法收敛速度优于其他算法且文中算法得到了目前的mk08算例的最优解。 图6 mk08算例求解收敛图 图7为文中算法对mk08算例的最佳调度甘特图,查阅mk08算例的源文件得知任何工件的任何工序都没有涉及到使用机器6,从图中也可以看到机器6为空闲状态,从而也从侧面验证了文中算法的可行性与正确性。 图7 mk08算例调度甘特图 针对柔性作业车间调度中最小化最大完工时间单目标,提出一种融合遗传算法与混合蛙跳算法的混合算法。对遗传算法的变异与交叉规则根据柔性作业车间调度问题的特性进行了改进,合理改进了算法搜索过程的广度与深度。通过对Brandimarte算例的测试,验证了该算法的可行性与有效性。并运用混沌理论生成随机数以使初始解在解空间分布更均匀,设计一种存优策略,且运用混合蛙跳算法提高了局部搜索能力。在未来的研究中,将考虑优化数学模型,考虑更多影响因素,并且考虑与文献[14]所用布谷鸟算法融合,使其更符合实际的生产环境。3.3 选择操作
3.4 交叉操作
3.5 OS部分的交叉操作
3.6 变异算子
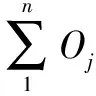
3.7 优良种子库
4 算法测试与数值实验
4.1 实验环境与参数设置
4.2 测试用例及实验结果
5 结束语

