基于PageRank的业务过程活动重要性度量
高 涛,周 彪,孔 会,艾合买提尼牙孜,郁 湧,3
(1.云南经济管理学院 教育学院,云南 昆明 650033;2.云南大学 软件学院,云南 昆明 650504;3.云南省软件工程重点实验室,云南 昆明 650504)
0 引 言
在当今激烈竞争的环境下,企业要想能够很好地生存、发展并扩大其竞争优势,就迫切需要用系统的方法和工具对其业务过程进行分析、优化和管理,因而业务过程管理得到了学术界和工业界的普遍重视。业务过程管理是致力创新企业业务过程管理、分析、控制与改进的系统化和理论化方法,目的是为了使企业能够不断改进产品质量和提升其服务水平[1]。
业务过程管理就是从企业的业务过程出发来对其业务过程进行全方位的管理和分析,并能够支持企业对业务过程的不断持续改进,从而在理论上和实践上都具有广阔的研究空间和应用范围[2]。业务过程管理自从开始受到国内学者和相关研究人员的关注[3-4]以来,已在多方面、多角度取得了一系列的研究成果:
在协同业务过程的建模方法和正确性分析方面,文献[5-6]提出自顶向下建模方法,并在此基础上从契约中生成对应组织的相关业务过程;文献[7]采用自底向上建模方法来定义企业自身的业务过程,并用它来构建具有协同功效的协同业务过程;文献[8-9]根据正确性约束对业务过程内部结构进行修改以自动构建满足正确性约束的业务过程;文献[10]结合Petri网和过程挖掘来提出一种针对协同业务过程的修正方法;文献[11]基于模型检测技术提出一种需求一致性检测方法,实现需求一致性自动验证;文献[12]在兼顾同步和异步交互的基础上,用简单路径来刻画协同业务过程的行为。
在业务过程时间预测方面,文献[13]使用了一种机器学习算法对业务过程进行剩余执行时间的预测;文献[14]根据发现的业务流程特征之间相关性来对业务过程剩余时间进行预测;文献[15]考虑事件的附加属性以改进时间预测质量;文献[16]提出一种结合回归与联合概率矩阵分解的时间预测方法;文献[17]提出一种基于依赖关联度的噪声日志过滤方法,通过轨迹可达性分析去除日志中的噪声;文献[18]构建一个嵌套的预测模型和使用嵌套模型树回归算法进行完成时间的预测;文献[19]提出基于控制流分析技术来预测运行过程实例剩余时间的白盒方法;文献[20]提出了基于贝叶斯网络的称为CRAFFT的活动预测方法。
虽然业务过程管理已经在多方面、多角度取得了很多的研究成果,但是,业务过程管理的管理对象多种多样,运行过程比较复杂。业务过程管理需要使用各种方法、技术和软件工具来设计、执行、控制和分析可执行的过程以及过程中涉及的人员、组织、应用、文档或其他信息资源[1]。为了能够很好地对业务过程中的资源和人员进行合理的配置和调配,使其能够高效准确地运行,这就需要对业务过程中的活动之间的关系和活动的重要性进行分析和度量,从而根据活动的重要性来合理分配资源。为此,该文在基于Petri网表示的业务过程基础上,对业务过程中活动之间的依赖关系进行分析和度量,并借鉴PageRank算法的思想来提出一种业务过程活动重要性度量的指标和方法。
1 业务过程模型的形式化表示
业务过程指一个或一系列连续有规律的行为以确定的方式发生或执行,产生特定结果。Davenport和Short将业务过程定义为“以达成特殊业务成果目标的一系列有逻辑相关性的任务”和“企业过程是一系列结构化的、可测量的活动的集合,并为特定市场或特定顾客产生特定输出”[21]。在业务过程管理的相关方面,研究人员通常使用Petri网来对业务过程进行直观的描述,从而以便于人们之间的沟通和理解。Petri网是德国科学家Petri博士于1962年在其博士论文《用自动机通信》中提出的一种网状结构的理论模型[22],Petri网和业务过程模型的表示如下:
定义1 Petri网[23]。Petri网是一个四元组∑=(P,T;F,M),其中:
(1)P∪T≠∅,P为库所集,T为变迁集;
(2)P∩T=∅;
(3)F⊆(P×T)∪(T×P),F是有向弧集,表示∑上的流关系;
(4)映射M:P→{0,1,2,…}称为Petri网的一个标识。通常用M0表示Petri网的初始标识。
定义2 前集[23]。设∑为一个Petri网,若x∈P∪T,·x={y∈P∪T|(y,x)∈F},则称·x为x的前集。
定义3 后集[23]。设∑为一个Petri网,若x∈P∪T,x·={y∈P∪T|(x,y)∈F},则称x·为x的后集。
定义4 工作流网[24]。Petri网WF-net=(P,T;F,M)是工作流网,当且仅当:
(1)存在一个源库所i∈P,使得·i=∅;
(2)存在一个汇聚库所o∈P,使得o·=∅;
(3)每一个节点x∈P∪T都位于从i到o的一条路径上。
工作流网是荷兰业务过程领域专家Aalst教授在Petri网的基础上提出来的一种业务过程的建模工具,目前已经成为组织内业务过程管理和控制流建模的首选模型之一,因此,该文就用工作流网来表示业务过程。在工作流网中,库所集P={p1,p2,…,pn}表示业务过程中的n个不同状态、阶段或者条件等;变迁集T={t1,t2,…,tm}表示业务过程中m个不同的活动,有向弧集F表示业务过程中的控制结构关系。在业务过程中,存在4种基本的控制结构,即:顺序、并行、选择和循环,其表示方式如图1所示。
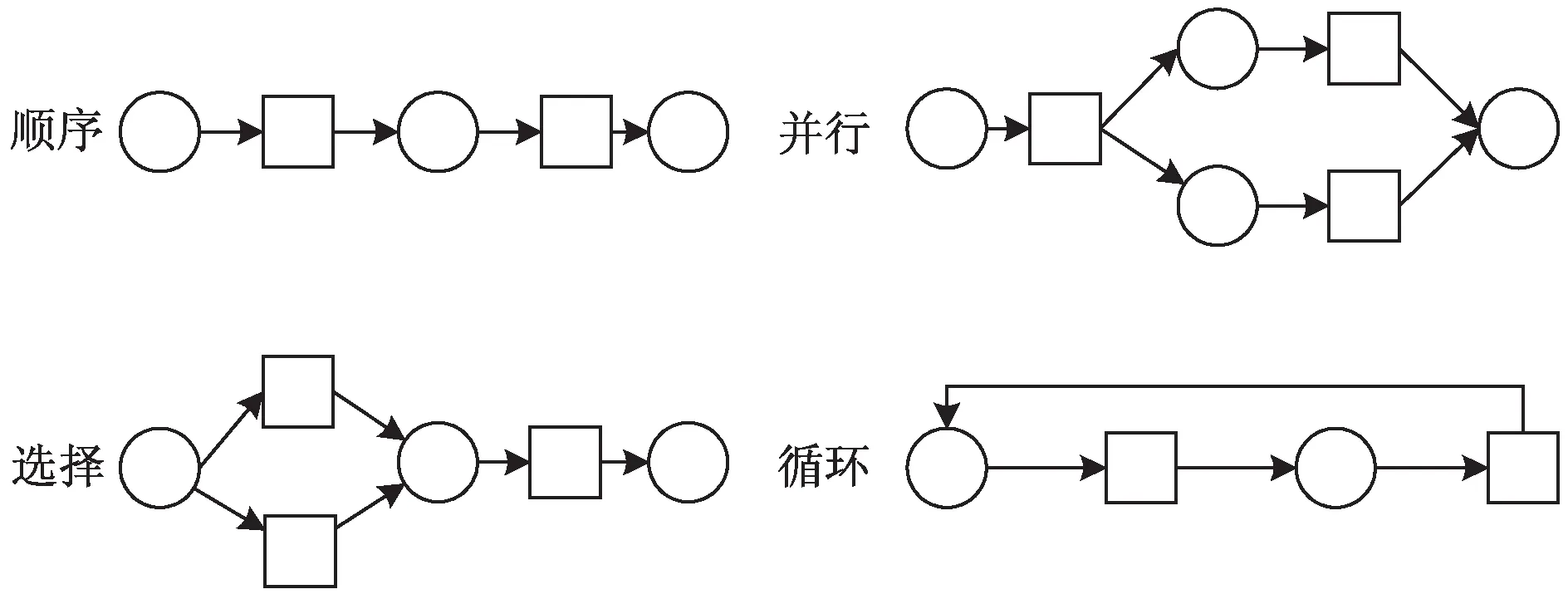
图1 Petri网中的控制结构
2 业务过程中活动之间依赖关系分析和度量
业务过程是以达成特殊业务成果为目标的一系列有逻辑相关性和有规律的活动的集合,因此,业务过程中的活动之间会存在一定的依赖关系。本部分在基于Petri网表示的业务过程基础上,通过分析业务过程中活动之间的相关性来进行依赖关系的分析和度量。
定义5 依赖关系。对于一个业务过程WF-net=(P,T;F,M)中的两个活动ti,tj∈T,如果满足活动tj的执行要以活动ti的后集为前提,即ti·∩·tj≠∅,则称活动tj直接依赖于活动ti,表示为tj→ti;否则称活动tj不直接依赖于活动ti。
如果活动tj直接依赖于活动ti,则活动tj称为依赖的活动,活动ti称为被依赖的活动。业务过程中活动之间的直接依赖关系和依赖程度由业务过程中活动之间的控制结构和活动的使能条件来共同决定。
比如,在图2(1)的顺序结构中,活动t2的前集是活动t1的后集,因此,活动t2直接依赖于活动t1,并且活动t1没有执行的情况下,活动t2就得不到执行,因此,可以认为活动t2完全依赖于活动t1。在图2(2)中,活动t5的前集是活动t3和活动t4的共同后集,活动t5直接依赖于活动t3或者活动t4,只要活动t3或者活动t4有一个执行,活动t5就可以执行,因此活动t5只是部分依赖于活动t3或者活动t4;但是活动t3和活动t4是并行结构,它们的执行是同步的,而它们之间没有直接依赖关系。同理可以看出,在图2(3)中,活动t8部分依赖于活动t6和活动t7;在图2(4)中,活动t10和活动t9之间具有循环结构,活动t10完全依赖于活动t9,而活动t9只是部分依赖于活动t10。
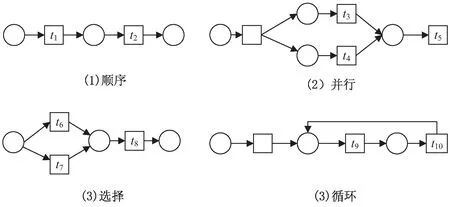
图2 不同控制结构中的直接依赖关系
从图2的示例可以看出,业务过程中不同活动之间的直接依赖关系的强弱是不一样的,可以把活动之间的直接依赖关系的强弱称为依赖关联度,它度量了当一个活动失效或者发生改变后对后继活动产生的影响程度。依赖关联度由所依赖活动的前集库所数和能够为其提供资源的活动数来确定,当能够提供资源的活动数越多时,对相应活动的依赖关联度就越小;反之,则越大。为此,在业务过程中,可以把活动之间的依赖关联度表示为:
定义6 依赖关联度。对于一个业务过程WF-net=(P,T;F,M)中的两个活动ti,tj∈T,如果活动tj直接依赖于活动ti,即ti·∩·tj≠∅,则活动tj对活动ti的依赖关联度Dtj→ti的取值为:
其中,|·tj|表示活动tj的前集·tj中所含库所的数量,而|·x|、|{ti}∩·x|分别表示·x、{ti}∩·x中所含活动的数量。业务过程中所有活动之间的依赖关联度可以用一个m×m的邻接矩阵DL=(Dij)m×m表示,称为活动之间依赖关联度邻接矩阵,其中:
从活动之间依赖关联度的计算公式(1)容易看出,活动tj对活动ti的依赖关联度Dtj→ti的取值范围为[0,1]。当活动tj对活动ti没有直接依赖关系时,其依赖关联度取值为0;活动tj对活动ti具有完全的依赖关系时,其依赖关联度取值为1。
3 基于PageRank的业务过程活动重要性度量
3.1 PageRank算法
PageRank算法[25]是搜索引擎中用于网页排序的经典算法,其目的就是通过计算页面链接的数量和质量来确定和标识网站的重要性并进行网页排名。该算法是基于“从优质网页链接而来的网页必定还是优质网页”这样的思想和回归关系,也就是:当某个网页pj有一个连接指向网页pi,就认为pi获得了pj对它贡献的分值,该值的多少取决于网络pj本身的重要程度,即网页pj的重要性越大,网页pi获得的贡献值就越高。由于网络中网页之间连接关系具有相互指向性,因此,网站中各个网页的重要性计算就是一个不断迭代的过程,最终网页可以根据重要性的得分值来进行检索和排序。在PageRank算法中,它把网页之间的链接关系看成一个有向图,然后根据网页之间的相互链接结构来实现的,算法的表达式为:
其中,p1,p2,…,pn表示网页;M(pi)表示待研究网页pi的网页链入数;L(pj)表示网页pj的网页链出数;n表示网络中的所有网页数量;PageRank(pi)表示网页pi的PageRank值,所有网页的PageRank值构成网络的PageRank向量;q为阻尼系数,用来表示任意时刻用户在浏览某个网页之后还会继续浏览它之后的网页的概率。通常情况下,阻尼系数的取值为0.85。
根据公式(2)可知,如果指向某个网页pi的链接数目越大,链接源对应的网页的重要性越高,则该网页pi就越重要,从而计算出来的PageRank值也就越大。
3.2 基于PageRank算法的活动重要性度量
在业务过程中,根据活动之间的直接依赖关系和依赖关联度邻接矩阵,可以构建对应的加权网络有向图。在此有向图中,节点就是业务过程中的活动,而节点之间边的方向和权重由活动之间的直接依赖关系和依赖关联度来确定。因此,可以将PageRank算法的思想引入到业务过程的活动重要性度量中,从而提出一种业务过程活动重要性评估的指标和方法。
对于业务过程WF-net=(P,T;F,M)中的活动ti∈T来说,如果活动tj直接依赖于活动ti,则活动tj的重要性对活动ti的重要性取值有贡献;活动tj的重要性越大,活动ti获得的贡献值就越高。同时,在业务过程中,不同直接依赖关系的活动之间的关联度并不完全相同,依赖关联度的大小对活动之间的贡献值也会有所差异,依赖关联度越大,则对应的贡献值也就越高。因此,根据业务过程的特点,在考虑活动之间依赖关联度的情况下,一个活动的重要性由依赖于它的活动的重要性及其它们之间的依赖关联度来共同决定,用公式表示为:
(3)
其中:
(1)AR(ti)表示活动ti的重要性取值;
(2)(ti·)·表示依赖于活动ti的所有活动的集合;

(4)m表示业务过程中的所有活动的数量;
(5)q为阻尼系数,表示业务过程中活动重要性依赖于其他活动的程度,阻尼系数越大,活动重要性的依赖程度就越大。
在业务过程中,由于活动之间具有顺序和循环等交互关系,活动之间的依赖关系具有传递性,这使得活动的重要性计算是一个迭代过程。因此,在计算活动的重要性过程中可以用向量Si=(AR(t1,i),AR(t2,i),…,AR(tm,i))来表示第i次迭代获得的活动重要性取值,向量Si和活动取值AR(t1,i)中的下标i表示迭代的轮次。迭代过程中,可以用概率转移矩阵Q来记录一个活动到达另一个活动的概率,概率转移矩阵Q由活动之间依赖关联度来确定,表示为:
(4)
由于各个活动重要性取值的计算存在迭代性,为此,可以为业务过程中所有活动设置一个初始得分,即:
S0=(AR(t1,0),AR(t2,0),…,AR(tm,0))=
然后用活动的重要性计算公式(3)来更新所有活动的重要性取值,不断迭代,直到活动重要性向量Si=(AR(t1,i),AR(t2,i),…,AR(tm,i))的取值收敛为止,这样就可以快速地求出业务过程中每个活动的重要性。
4 实验结果与分析
实验部分将利用该文提出的依赖关系分析和重要性度量方法对现实的业务过程模型中活动之间的依赖关系和活动的重要性进行分析和度量,并根据实验结果来分析该算法的合理性和有效性。
4.1 实验模型选取和描述
本实验所选取的两个业务过程模型,一个是电子政务中工厂报建审批业务过程[26],另一个是公司处理用户投诉的业务过程[27],这些业务过程模型都包括顺序、并行、选择和循环等结构,具有一定的代表性。
在工厂报建审批业务过程中,申报人首先需要根据自己的情况来如实填写和提交申报材料,然后再进行政策法规方面的预审;如果预审通过,那么相关的申报材料就必须在30天之内完成环保部门的审批;否则原来的预审结论就会失效,必须重新进行预审。工厂报建审批业务过程用Petri网表示,如图3所示,业务过程中各个活动表示为:
t1:填写和提交申请材料;t2:预审批;t3:规划审批;t4:环保审批;t5:活动超时处理;t6:数据超时处理;t7:综合审批;c1、c2、c3为连接符。

图3 工厂报建审批的业务过程
在处理用户投诉的业务过程中,当公司接到客户投诉时,首先需要对客户的投诉信息进行登记,然后同步处理向客户寄出调查表和对投诉进行评估这两个活动;如果客户能够在14天之内返回调查表,则任务调查表和后续的活动就会被执行,否则,将会被抛弃。对于返回的调查表,公司会根据评估的结果来确定是否需要对该投诉进行处理。在处理用户的投诉业务过程中,都是通过任务检查进程进行检查,然后进行归档,从而结束整个过程。处理用户投诉的业务过程用Petri网表示,如图4所示,业务过程中各个活动表示为:
t1:登记;t2:寄出调查表;t3:投诉评估;t4:过期处理;t5:调查表处理;t6:投诉不需要处理;t7:投诉需要处理;t8:处理投诉;t9:检查处理结果;t10:检查不合格;t11:检查合格;t12:归档。

图4 处理用户投诉的业务过程
4.2 实验分析
本节利用提出的依赖关系分析和重要性度量方法对选取的两个业务过程模型中活动之间的依赖关系和活动的重要性进行分析。在进行活动重要性度量时,本实验中的阻尼系数q按照通常的取值为0.85。同时,由于基于PageRank的业务过程中活动的重要性度量得到的重要性取值一般都比较小,为了使结果具有可区分度,本实验中对每个活动的重要性取值都除以对应业务过程中活动重要性取值的最大值来进行归一化处理,即:
(5)
在对业务过程进行依赖关系分析和重要性度量之后,可以根据活动之间依赖关系和重要性度量的结果构建对应的加权网络有向图来进行表示,其中节点为不同的活动,节点之间的边表示活动之间的直接依赖关系,边的方向为直接依赖关系的方向,边上的权重为活动之间的依赖关联度。这样,工厂报建审批和处理用户投诉的业务过程对应的依赖关联度和活动重要性取值的网络有向图分别如图5和图6所示,其中活动下方的值为活动的重要性取值。

图5 工厂报建审批业务过程的依赖关系和活动重要性
从图5的结果可以看出,在工厂报建审批的业务过程中,各个活动的重要性大小关系为:
AR(t5)>AR(t4)>AR(t1)=AR(t6)>AR(t2)
>AR(t3)>AR(t7)
(注:由于c1、c2、c3为连接符,没有比较重要性的必要,因此就做省略处理。)
其中,活动t5(活动超时处理)和活动t4(环保审批)重要性取值较大,而活动t7(综合审批)的重要性取值较小。这样的结果与工厂报建审批的实际情况是一致的,因为在具体业务中活动超时处理和环保审批阶段的工作都比较重要,应该重视或者分配更多的资源;而综合审批阶段由于是报建审批业务中的收尾环节,因此重要性相对会弱一些。
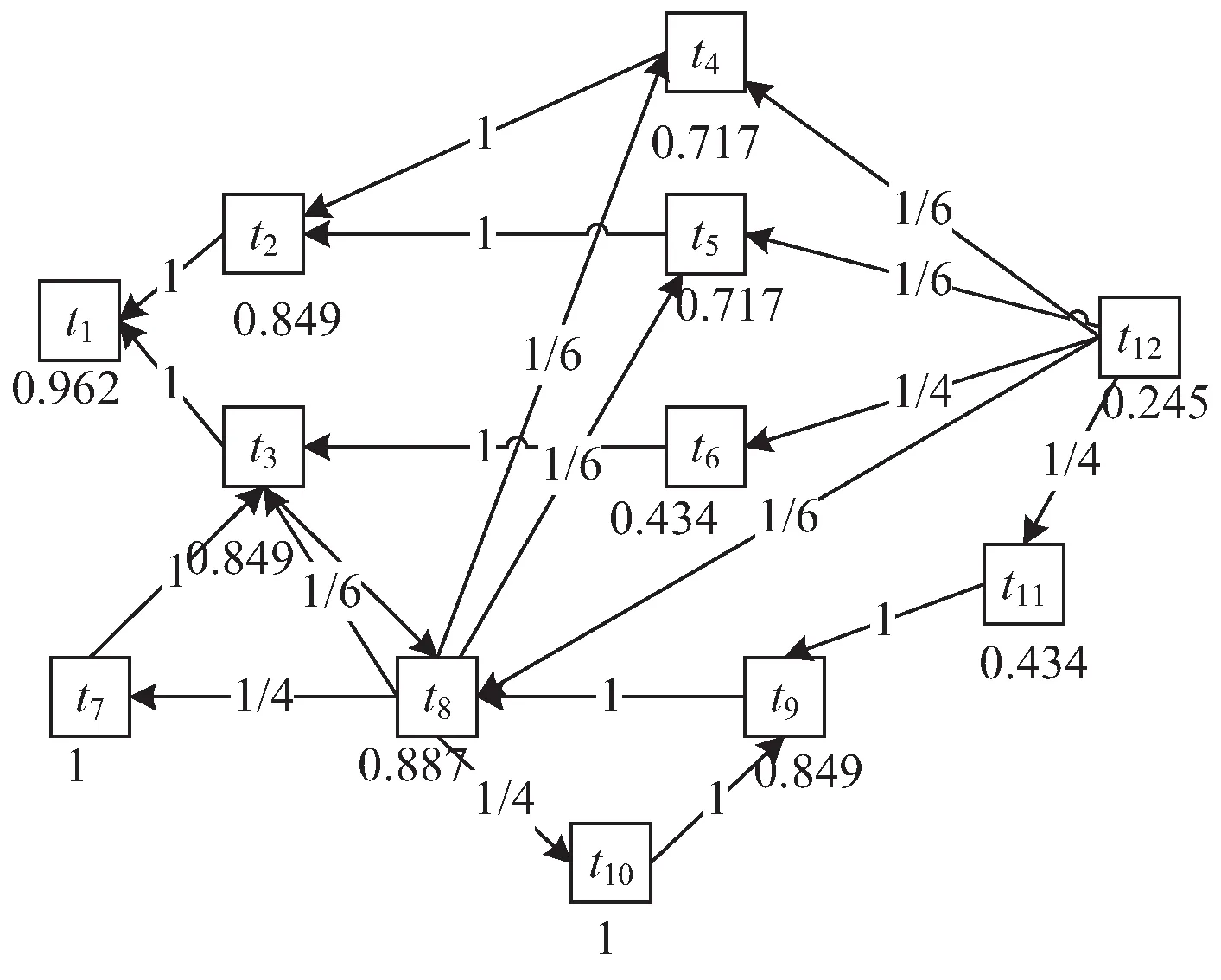
图6 处理用户投诉的业务过程的依赖关系和活动重要性
图6所示的处理用户投诉的业务过程中,各个活动的重要性大小关系为:
AR(t7)=AR(t10)>AR(t1)>AR(t8)>AR(t2)
=AR(t3)=AR(t9)>AR(t4)=AR(t5)
>AR(t6)=AR(t11)>AR(t12)
根据重要性大小关系可以看出,活动t7(投诉需要处理)和活动t10(检查不合格)的重要性取值最大,活动t12(归档)的重要性取值最小;在其他活动中,活动t2与活动t3、活动t4与活动t5之间是并行关系,因此它们之间的重要性取值相同;此外,从重要性取值可以看出活动t1(登记)和活动t8(处理投诉)比活动t2(寄出调查表)重要;活动t3(投诉评估)与活动t9(检查处理结果)同样重要;活动t4(过期处理)比活动t6(投诉不需要处理)等。这些活动重要性取值的结果与处理用户投诉过程的实际情况具有很大的吻合性与一致性。
总之,在业务过程活动依赖关系分析和度量的基础上,借鉴PageRank的思想来提出的活动之间重要性度量方法,在对工厂报建审批业务过程和处理用户投诉业务过程中活动重要性度量和排名分析方面获得的结果比较符合现实业务过程的情况,说明提出的算法具有一定的合理性和有效性。
5 结束语
业务过程管理是企业用来对其业务过程进行管理、分析、控制与改进的系统化和理论化方法,业务过程管理的最终目标在于通过进行业务过程的管理来不断提高和改进所生产产品的质量,并提升其自身的服务水平。近年来,虽然业务过程管理已经在多方面、多角度取得了一系列的研究成果,但是,针对业务过程中活动的重要性度量方面的研究,尚属鲜见。然而,合理分析业务过程中活动之间的依赖关系并给出活动的重要性度量和排名,是进行活动的资源和人员合理的配置和调配的关键之一。为此,在基于Petri网表示的业务过程基础上,提出了一种业务过程中活动之间的依赖关系分析和活动重要性度量的方法。主要工作如下:(1)根据业务过程中活动之间的控制结构和活动的使能条件来对活动之间的直接依赖关系进行分析;(2)基于活动之间的直接依赖关系和依赖关联度取值来构建活动之间的加权网络有向图,并将PageRank的思想引入到业务过程的活动重要性度量中,提出一种业务过程活动重要性评估的方法;(3)以现实中的工厂报建审批业务过程和公司处理用户投诉的业务过程为案例进行分析和研究,根据实验结果来分析该算法的合理性和有效性。结果表明,在业务过程中活动的依赖关系分析的基础上,结合PageRank算法来提出的活动重要性度量和排名的方法,具有较好的表现效果。

