基于多频激励下振动响应的GIS 机械缺陷诊断方法

吴旭涛，赵晋飞，马云龙，，何宁辉，，马波，李军浩

（1.国网宁夏电力有限公司电力科学研究院，银川 750011；2.西安交通大学电力设备电气绝缘国家重点实验室，西安 710049）

0 引言

近年来，电力系统的规模不断扩大、输电容量不断增加，这对电力系统的可靠性和经济性也提出了越来越高的要求[1-5]。SF6断路器具有开断能力强、安全可靠性高、节省占地面积、易于维护、环境适应能力强等优点，在高电压等级的输电线路中的被广泛采用。然而GIS 设备因其采用全金属封闭结构，其内部机械结构较为复杂和庞大，一旦发生故障，影响范围大且难以准确定位及快速抢修，影响故障后的设备投运，导致严重的经济损失。因此，及时有效发现GIS 设备内部潜伏性缺陷并准确判断GIS 设备内部缺陷类型及位置，对保障GIS 设备安全稳定运行具有重要意义[6-9]。

设备运行时的振动信号可以有效反映机械状态，是表征设备机械特征的重要参数[10-12]。因为振动信号具有不受电磁辐射干扰的优点，所以受到专家学者的广泛关注，被应用于各类电力设备的机械缺陷诊断并取得了成功应用。马宏忠团队研究了三相分箱式和共箱式GIS 的振动产生机理，并对GIS 母线筒的模态特性进行了仿真分析[13-14]。刘宝稳基于AlexNET 模型断路器分合闸时的机械故障进行识别[15]；高凯通过温升下的振动信号特征提出了检测触头接触程度的方法[16]。赵洪山利用粒子滤波算法对GIS 振动信号进行分析，结合自适应阈值方法实现了GIS 机械缺陷的诊断[17]。吴旭涛利用有限元模型研究了螺栓松动时的GIS 振动信号传递特性[18]。上述研究通过对GIS 运行时的振动信号进行处理，实现了对GIS 机械状态的诊断。汲胜昌团队研究了变压器的振动机理和特性，并提出了一套基于扫频阻抗的变压器机械缺陷诊断方案[19]，但该方法还仅仅应用于变压器，并未在GIS 上进行尝试。振动频响法最早是在变压器上进行应用的，即通过机械或电激励的方法使得变压器绕组产生振动，同时在油箱表面布置测点采集振动信号，进而通过激励与响应的函数关系（振动频响函数）进行绕组状态的诊断[20]。GIS 也可以看作是一个复杂多自由度机械结构，其在一定的外加激励力作用下也会产生特定的振动响应。当对GIS 受到力锤式的机械脉冲激励或多频率的电激励时，会在外壳上产生特定的振动响应。通过检测GIS 在宽频机械或电激励下的振动响应，就能判断其是否存在结构变形等机械缺陷，这种方法也是传统的机械结构模态分析方法在电力设备中的扩展应用。

基于上述振动频响法的思路，本文通过对GIS施加不同频率机械力激励的方法进行激振，同时检测此时母线筒的振动响应信号，在保证激励不变的情况下，对比分析GIS 正常及存在机械缺陷时的振动频率响应特性，从而提出一种GIS 机械状况的诊断方法，这对于保证GIS 的安全稳定运行具有指导意义。

1 GIS振动测试平台

1.1 多频振动激励方法

1）机械激励：借助于试验模态分析的方法进行，即人为地对GIS 外壳施加动态机械激励，然后采集GIS 母线筒多点的振动频率响应信号[21-26]。这种动态机械激励以输入激励力的信号特征有多种形式，包括：正弦扫描（多个频率的激励依次施加）、稳态随机（包括白噪声、宽带噪声或伪随机，同时输出多个频率的激励力，对被测设备进行激励）、瞬态激励（如采用力锤敲击的方式，所施加的实际上是一个脉冲力的形式，其频域分布较宽）等。此外，由于GIS 中断路器操动时会产生很大的暂态振动，相当于一个暂态的机械激励，会导致GIS 本体产生振动响应，对其进行分析有望检测GIS 存在的机械缺陷。

2）多频正弦波激励：采用多频率合成的大电流发生器，直接在GIS 母线上施加不同频率的大电流，然后测量此时外壳上多点的振动信号，得到其振动频率响应。

工程中常采用基于大功率三极管的信号放大技术和基于SPWM 的开关电源技术两种方式实现多频率大功率信号合成。基于大功率三极管的信号放大技术先用数模变换产生与所需信号波形相同的小信号（功率小，电压低），然后利用大功率三极管的放大特性对该信号进行功率放大。这种方法的优点是信号高保真，因为三极管工作在线性区，放大前后的信号可以保持高度一致，信号波形很纯净，几乎不存在干扰。三极管工作在线性区的缺点是工作效率很低，而发热很高。当采用这种原理的电源带无功负载时，发热问题将更为严重，所以这种工作方式的电源带无功能力很差，一般不超过其总容量的20%；另外一种实现方法是使用SPWM 工作方式的开关电源，其利用大功率IGBT元件来实现多频率信号的输出，可以有效解决功耗发热和带无功问题，但其缺点是输出信号中存在因开关过程引入的高频干扰。由于GIS 设备本身可等效于一电容元件，在实验时需要大量的无功，所以用SPWM 工作方式的电源更符合要求。

3）采用衰减振荡冲击电流激励：这种方法是一种等效于多频率正弦波电流激励的方法，采用冲击电流的产生回路，电容器充电后对被试GIS 放电，使得该冲击电流产生回路工作在欠阻尼状态，从而产生衰减的振荡冲击电流，调整合理的电路参数可改变振荡频率，从而等效于不同频率正弦波的激励。

上述3 种方法，机械领域一般都是采用第一种方式，但这种方法一般是在外壳表面激励，与GIS实际上是导杆流过大电流而受力存在差别，且由于GIS 设备刚度和质量重，对机械激励装置要求输出的激励要求较高。第2 种方法是一种较常规的方式，已经应用于变压器、电容器等设备的振动频率响应测试，由于需要输出大电流，对设备功率要求较高，一般大功率多频输出设备还包含有高频变压器，整个装置的体积大、重量重，在现场应用时存在困难。第3 种方法是一种等效的方法，输出的是一种振荡衰减的电流，但一般持续时间较短，且实际电流逐渐减小，是一种幅值变化的多频激励方式。

1.2 振动测试平台

上述3 种方法基本原理都是类似的，可根据实际进行选择使用。为测量不同频率力激励下的GIS振动信号，在实验室搭建了如图1 所示的振动测试平台。该平台由多频激励产生装置、252 kV GIS、振动加速度传感器、数据采集卡、信号采集系统组成。整个平台可以分为激励回路和振动测试回路。

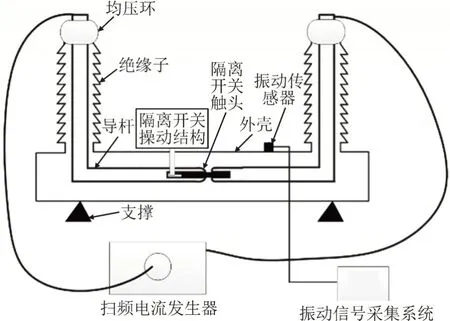
图1 振动测试平台Fig.1 Vibrationtest platform

激励回路：可按上述3 种方式进行选取，从原理上得到的结果是类似的。本文选取的是多频率的类正弦波电流激励，使得GIS 导杆分别流过不同频率的电流信号，激励其振动。

振动测试回路：将振动加速度传感器粘贴于GIS 外壳上，然后通过数据线和采集卡将传感器连接至信号采集系统。

1.3 振动信号采集装置

振动传感器可以分为振动位移传感器、振动速度传感器、振动加速度传感器。振动位移传感器是基于电器感应原理进行测量，易受到电磁辐射的干扰，不适合用于电力设备振动信号的测量；振动速度传感器频响范围较小，无法满足断路器分合闸振动信号的测量要求；振动加速度传感器具有灵敏度高、频响范围宽、抗电磁干扰能力强的优点，常被用于各类振动信号测量。实验过程中采用的振动加速度传感器主要参数见表1。

表1 振动加速度传感器参数Table 1 Parameters of vibration acceleration sensor

1.4 振动信号测量系统

本文使用的GIS 振动信号测量系统界面见图2。该系统可以实现测量频率调节、测量时长调节、时域波形显示、自动触发采集、自动保存、频域分析等功能。

图2 振动信号测量系统Fig.2 Vibration signal measurement system

测量得到的振动信号见图3。

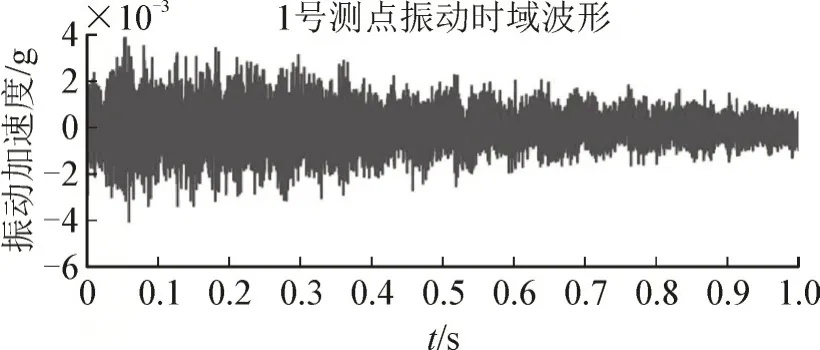
图3 振动响应信号Fig.3 Vibration response signal

2 数据分析方法

2.1 小波时频分析

目前，常用的振动信号处理方法是基于快速傅里叶变换的频域分析法。快速傅里叶变换是将振动信号转化为一系列不同频率正弦函数的组合，得到信号的不同频率分量。扫频电流激励下的振动信号为非稳态信号，信号的频率分量随时间不断变化，快速傅里叶变换只能显示信号包含的频率分量，并不能有效展现信号频率随时间的变化规律。本文除频域分析外，还采用小波时频分析对振动信号进行处理。小波变换的公式为

可以看出，小波基函数ψ有两个变量：尺度a和平移量τ。尺度a控制小波函数的伸缩，对应于频率；平移量τ控制小波函数的平移，对应于时间。经过小波变换后，既可以得到信号包含的频率分量，又可以得到信号频率随时间的变化规律。

2.2 梯度矩阵

梯度矩阵（matrix of oriented gradient，MOG）是通过计算图片像素值变化速率来提取特征值。因此，他可以描述图像的形状特征和像素的变化情况。具体计算步骤如下：

1）计算梯度。设某图片的像素值见图4，以该图片为例介绍梯度的计算方法。

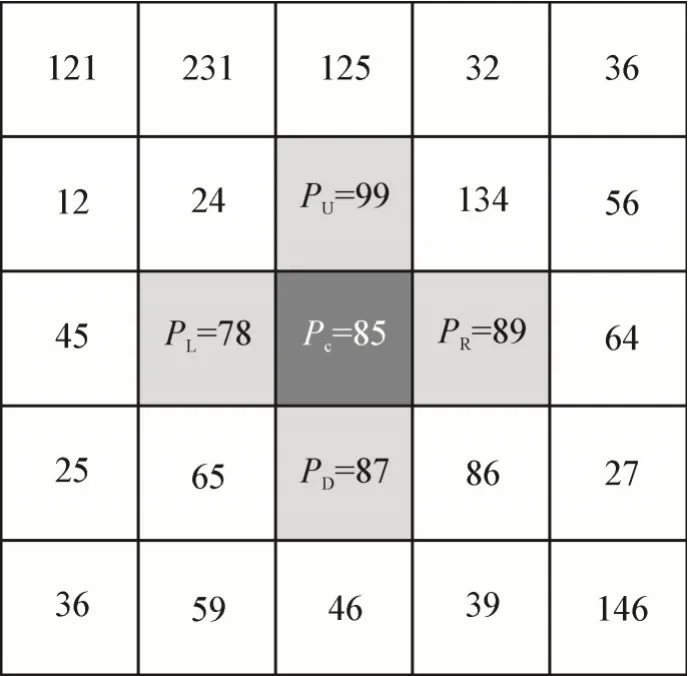
图4 图片的像素值Fig.4 Pixel value of the image

设像素点Pc的梯度值为Gc，那么Gc的幅值|Gc|和相角φ可以按照以下步骤计算为

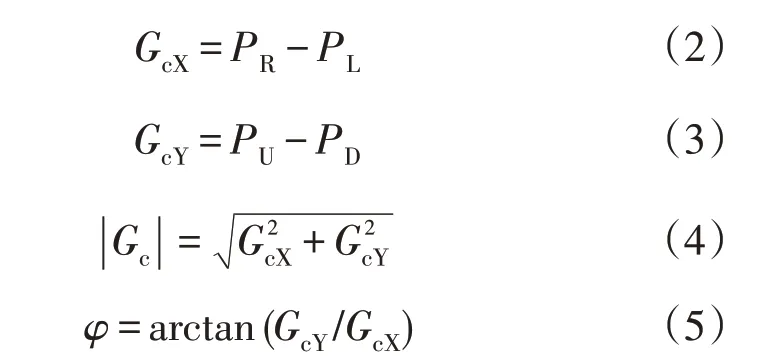
2）计算梯度向量。将图片中每16×16 个像素矩阵设为一个像素元胞。将0°～360°等分为9 个间隔，每个间隔为40°。根据像素梯度的X分量GcX和相角φ，可以把像素的梯度分别划分到各个区间内。以图3 中的Pc为例，GcX=11＞0，0°＜φ=36°＜40°，|Gc|=13.6。因此，Pc属于第1 个间隔，将他的梯度幅值按比例放入0°与40°，具体分配比例见图5。在像素元胞内不断重复以上步骤，将元胞内所有像素点的梯度幅值分别写入相应的间隔，就可以得到一个1×9 的向量，该向量就是像素元胞的梯度向量。

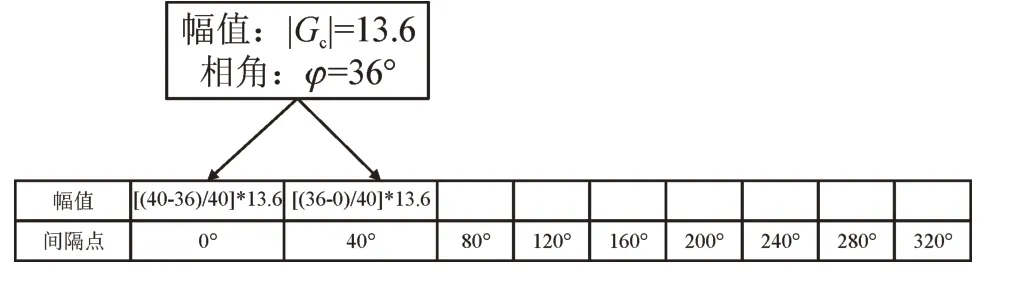
图5 梯度幅值分配Fig.5 Gradient amplitude distribution

3）归一化。为了消除信号中背景噪声的影响，对上述步骤得到的梯度向量进行归一化处理。将2×2 即4 个像素元胞设为一个像素块。将像素块内的4 个像素元胞的梯度向量组合成一个1×36 的向量，然后用向量中每个元素除以该向量的模，便可以得到归一化之后的梯度向量（normalized gradient vector，NGV）。在整个图片上重复上述步骤，便可以得到该图片的归一化梯度矩阵（normalized gradient matrix，NGM）。

2.3 相似度

1）余弦相似度。余弦相似度（COS-Similarity）通过计算两个向量的夹角来描述两个向量之间的差异。这种相似性主要考虑方向而不是两个矢量的幅度一致性。NGM 被重构为一维向量，称为NGM-Vector。在使用方向信息时，他也可以使用NGM 中每个元素的幅度信息。余弦相似度计算方法为

2）差值平方和相似度。

差值平方和相似度（D-Similarity）通过计算两个NGM 之间的差异值来衡量相似度。假设P（图片的像素矩阵）的大小为m×n。

差值平方和相似度计算方法为

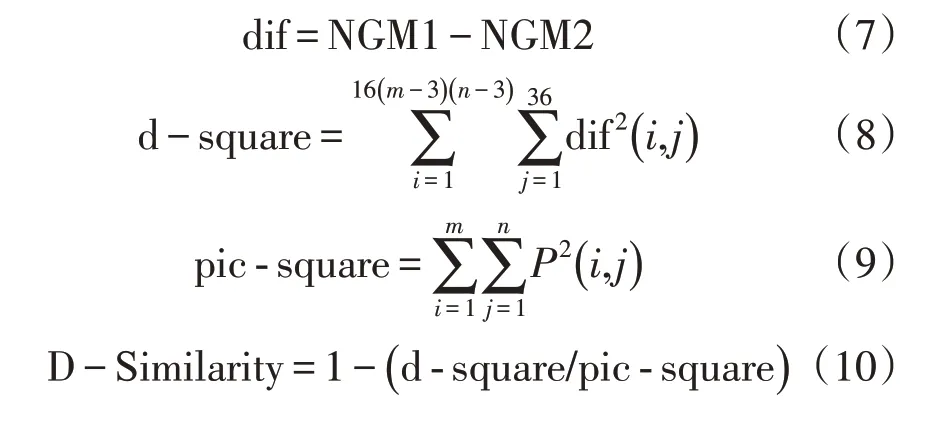
3 实验结果

为探究不同机械状态下的GIS 振动情况，本文在实验室252 kV GIS 上模拟了隔离开关接触不良缺陷，见图6。隔离开关的分合是由拐臂的转动实现的，通过调整隔离开关的拐臂角度即可调整隔离开关动静触头的接触程度。当拐臂位于图6 中上黑色线条所在角度时，隔离开关接触良好；当拐臂位于图10 中下黑色线条所在角度时，隔离开关接触不良。

图6 隔离开关缺陷模拟示意图Fig.6 Simulation schematic diagram of disconnect or defect

3.1 不同电流频率下的GIS振动特性

1）隔离开关接触良好。

激励平台输出的激励力频率为200～1 000 Hz 时，不同频率下GIS 振动响应信号的时频图见图7。图中右边颜色柱由下到上代表振动幅值由小到大。由图7 可知，不同激励频率下，GIS 振动响应信号的频谱几乎一致，响应信号的主频为1 200 Hz，持续时间为1 s；在1 500 Hz、1 700 Hz 处也出现了峰值，持续时间为0.7 s。

图7 时频图Fig.7 Time frequency diagram

2）隔离开关接触不良。

隔离开关接触不良时，激励力频率同样为200～1 000 Hz，不同频率GIS 振动响应信号时频图见图8。由图8 可知，不同电流频率下，GIS 振动信号的频谱几乎一致，振动响应信号的主频为850 Hz，持续时间为0.3 s；在1 200 Hz、1 500 Hz、1 700 Hz 处出现了峰值，其中1 200 Hz 持续时间为1 s，1 500 Hz 和1 700 Hz 持续时间为0.7 s。

图8 时频图Fig.8 Time frequency diagram

对比隔离开关接触良好和接触不良时的振动特性，可以看出，GIS 振动频率响应只与机械状态有关，不随激励频率的变化而变化。这是由一般机械激励力持续时间短，在GIS 外壳建立稳态振动之前，机械激励力的作用已经消失。GIS 的振动是瞬态激励下的非受迫振动，表现出GIS 的固有振动频率。因此，GIS 的振动频率响应只与其内部的机械状态有关。

3.2 不同机械状态下的时频图相似度

由于GIS 振动频谱不受激励力的频率影响，因此激励力的频率为200 Hz 时，测量隔离开关接触良好和接触不良时的振动响应信号各10 次，并计算每次振动与隔离开关接触良好时第1 次振动的相似度。结果见图9。可以看出，隔离开关接触不良时与正常状态下的相似度差异明显，其余弦相似度在0.5～0.6 之间，与正常状态下的相似度差值为约为0.2，变化率为27%；隔离开关接触不良后差值平方和相似度在0.25～0.3 之间，变化率约为50%。

图9 时频图相似度Fig.9 Similarity of time frequency diagram

3.3 隔离开关接触不良诊断方案

如图9 所示，当隔离开关接触不良时相似度会显著降低，变化率在20%～50%。因此，本文基于时频图梯相似度提出了一套用于隔离开关接触不良缺陷的检测方案，方法如下：

通过可输出多频率的机械激励发生装置对GIS施加多个频率的力作用，同时测量隔离开关处的振动信号，并计算该振动信号的时频图与正常情况的相似度。当COS-Similarity ∈[0.7，0.8]且D-Similarity ∈[0.4，0.5]，隔离开关正常无故障；当COS-Similarity ∈[0.5，0.6]且D-Similarity ∈[0.25，0.3]，隔离开关可能接触不良。

4 结语

基于多频机械激励产生装置和振动采集系，本文搭建了GIS 振动频率响应试验平台，实现了GIS在多频激励力作用下振动频率响应的测量，该平台也可模拟实际运行中常见的隔离开关接触不良缺陷。根据在多频力激励下GIS 振动响应信号的特点，利用小波时频分析的方法，对振动信号的时频域特征进行分析。主要结论如下：

1）在不同频率激励力作用下，GIS 振动只与内部机械状态有关，不随电流频率的变化而变化。

2）基于时频图的梯度矩阵相似度，本文提出了一种适用于诊断GIS 机械缺陷的方法。

3）给出了振动信号的时频图与正常情况相比时时频图梯度矩阵相似度的取值范围，能够对隔离开关接触不良缺陷进行有效诊断。

在今后的研究中，将继续对各种不同的多频激励方式进行对比，分析所获得的振动频率响应信号的异同，提出相应的激励设备参数、激励方式选择方法及技术改进方案等。此外，还应进一步对各类常见的GIS 机械缺陷进行模拟，实现多种机械缺陷的检测与识别方法，推进多频激励方式检测GIS 的机械状况的现场应用。