LCC-HVDC 换流站交流侧非特征次谐波产生机理与抑制方法研究

吴俊，黄弘扬，徐群伟，邱俊卿，袁敞

（1.国网浙江省电力公司电力科学研究院，杭州 310014；2.华北电力大学，北京 102206））

0 引言

基于电网换相换流器的高压直流输电（line commutated converter based high voltage direct current，LCC-HVDC）在大容量、远距离输电方面具有造价低、损耗小等独特的优势，现已成为了跨区域输电的主要手段[1-3]。目前我国已经建成投运的LCC 型高压直流输电工程有20 多个，其中较典型的有贵州—广东（贵广）、三峡—常州（三常）等±500 kV 高压直流输电工程以及向家坝—上海（向上）、云南—广东（云广）等±800 kV 特高压直流输电工程[4]。与±500 kV 的高压直流输电相比，±800 kV 的特高压直流输电有着更大的输送容量以及更远的输送距离，成为了我国“西电东送”工程的主要选择。

±800 kV 特高压换流站通常采用的是双12 脉动换流的方式，理想运行工况下换流器在交流侧只产生12k±1 次特征次谐波[5-6]，但是近年来通过对金华特高压换流站的电能质量测试发现：在大功率试验时，换流站500 kV 交流母线的4 次、5 次、7 次谐波电压含量分别为0.82%、1.92%、0.45%，远远超过了特征谐波11 次、13 次的0.21%、0.21%，并且12 脉动换流器内仍含有约0.4% 的5 次谐波电流，如果不采取相应的非特征次谐波抑制措施，那么这些谐波则会经过输电线路渗透到各个电压等级的电网中从而造成谐波污染，给电网的电能质量水平造成一定的影响。目前针对换流站出现非特征次谐波的原因以及分析方法，国内外已有相关的研究，文献[7]指出导致高压直流输电出现非特征次谐波的机理非常复杂，在早期的HVDC 项目中，主要和换流器的触发模式有关；文献[8-9]中提到交流电压的畸变、换流变压器三相阻抗不相等以及换流器触发角偏差是产生非特征次谐波的原因；文献[5，10]采用了开关函数法来分析特高压直流输电系统的非特征次谐波，这种方法可以克服调制理论准确性不足的问题；文献[11]建立了电压不平衡下12 脉动整流的频域谐波耦合导纳模型，该模型可以计算整流装置产生的谐波；文献[12]给出了各种不平衡条件下6 脉动换流器交流侧基波以及各次谐波的幅值表达式，但是缺失谐波相位的信息，因此无法用于12 脉动换流器的谐波分析；文献[13-14]采用了分段时域算法，通过列写换相回路方程以及边界条件，对不平衡条件下的交流侧谐波进行分析计算。以上研究均只对换流站出现非特征次谐波的原因进行了分析，但是没有提出相应的抑制措施。

传统用来治理LCC-HVDC 换流器向交流电网注入谐波的方式为在交流母线上安装大量的无源调谐滤波器，这种滤波器结构简单，可在较大程度上抑制换流站交流侧的特征次谐波，应用较为广泛，但是其缺点也很明显：无源滤波器的滤波效果容易受到系统阻抗的影响，如果滤波支路较多则很容易发生谐振[15-16]，从而加重谐波污染；无源滤波器的组数较多，体积大，占地面积大[17]；无源滤波器的调谐点是针对特征次谐波设计的，对非特征次谐波的抑制效果不好。基于无源滤波器存在的一些缺点，文献[18-20]提出了一种适用于LCC-HVDC 谐波治理的级联H 桥混合型有源滤波器（hybrid active power filter，HAPF），该滤波器耐高压、滤波效果好、占地面积小，但是在谐波电流补偿的控制上采用的是针对于特征次谐波的准比例谐振控制器并联的形式，因此只对特征次谐波进行了抑制。

本文首先建立了±800 kV 特高压直流输电的模型，并以金华换流站为例，分析了换流变压器三相阻抗不对称、晶闸管触发角存在偏差等因素对非特征次谐波的影响；然后针对传统无源调谐滤波器的一些缺点以及级联H 桥HAPF 控制上存在的不足，提出了一种基于级联H 桥的纯有源滤波装置，该滤波装置采用了PI 控制方法，可以抑制换流站交流侧的特征次谐波和非特征次谐波。最后在PSCAD/EMTDC 中搭建了±800 kV 特高压直流输电仿真模型和级联H 桥APF 的仿真模型，通过在平衡运行条件下和不平衡运行条件下对传统的无源滤波器和所提出的级联H 桥APF 的滤波效果进行对比，仿真结果表明级联H 桥APF 在特征次谐波以及非特征次谐波抑制上的有效性。

1 换流站非特征次谐波分析

1.1 金华特高压换流站模型

宾金直流工程金华特高压换流站采用400 kV+400 kV 双12 脉动换流器串联的接线方案，即换流站共有4 大组换流器，每极2 个串联组成800 kV，每大组换流器均为12 脉动换流器，其接线方案见图1。

图1 换流站接线简图Fig.1 Schematic wiring diagram of converter station

换流站内的无功补偿和滤波设备共有17 组，电压等级均为500 kV，无功总容量为4 879 Mvar，由9组HP12/24 滤波器和8 组SC 并联电容器组成，交流滤波器及并联电容器组见图2，HP12/24 滤波器及SC 并联电容器参数见表1、表2。

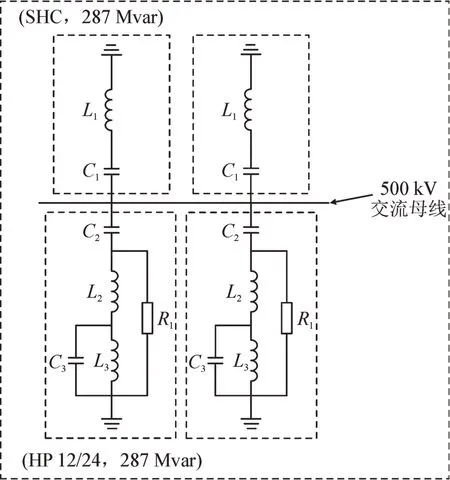
图2 交流滤波器及并联电容器组Fig.2 AC filter and shunt capacitor bank

表1 HP12/24交流滤波器参数Table 1 Parameters of HP12/24 AC Filter

表2 SC并联电容器参数Table 2 Parameters of SC shunt capacitor

1.2 非特征次谐波分析

对于12 脉动换流器的谐波分析本文采用了分段时域法，即通过列写6 脉动换流器在一个周期内换相期间和导通期间的电流表达式，再将得到的一个周期内的电流进行FFT 分解，可以得到其在交流侧产生的各次谐波电流幅值和相位，之后将组成12脉动换流器的两个六脉动换流器（YY 换流变连接的和YD 换流变连接的）在交流侧产生的谐波电流幅值相位进行叠加，即可得到12 脉动换流器在交流侧产生的谐波电流；以A、C 换相为例，列写换相期间A 相电流表达式，A、C 换相过程见图3。

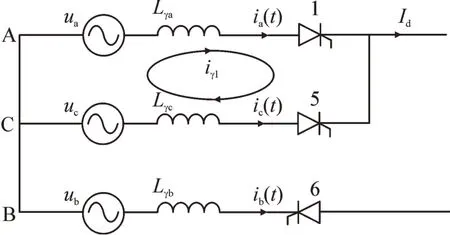
图3 A、C换相示意图Fig.3 Commutation schematic diagram between phase A and C

图中三相电压的公式为

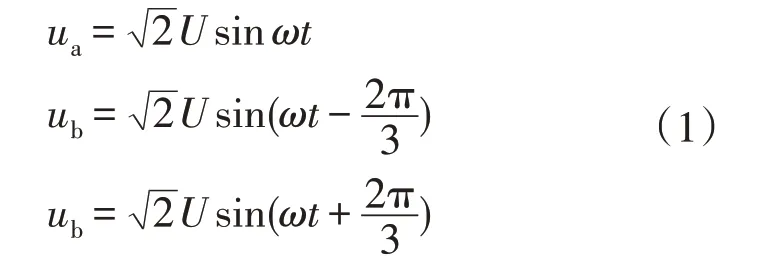
列写换相回路的KVL 方程为

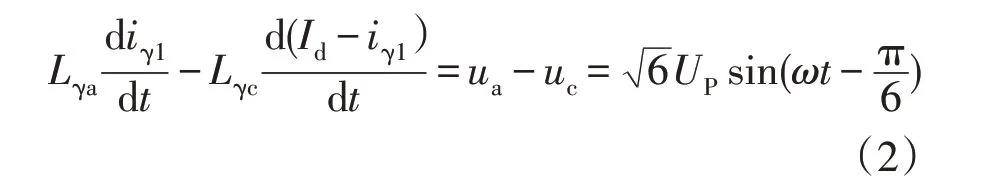
式中，Lγa、Lγb、Lγc分别为换流变压器三相电感。

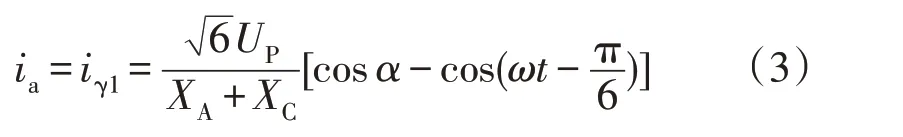
根据晶闸管的导通顺序，可得到半个周期内（另半个周期与其对称）的A 相电流表达式如公式（4）所示。

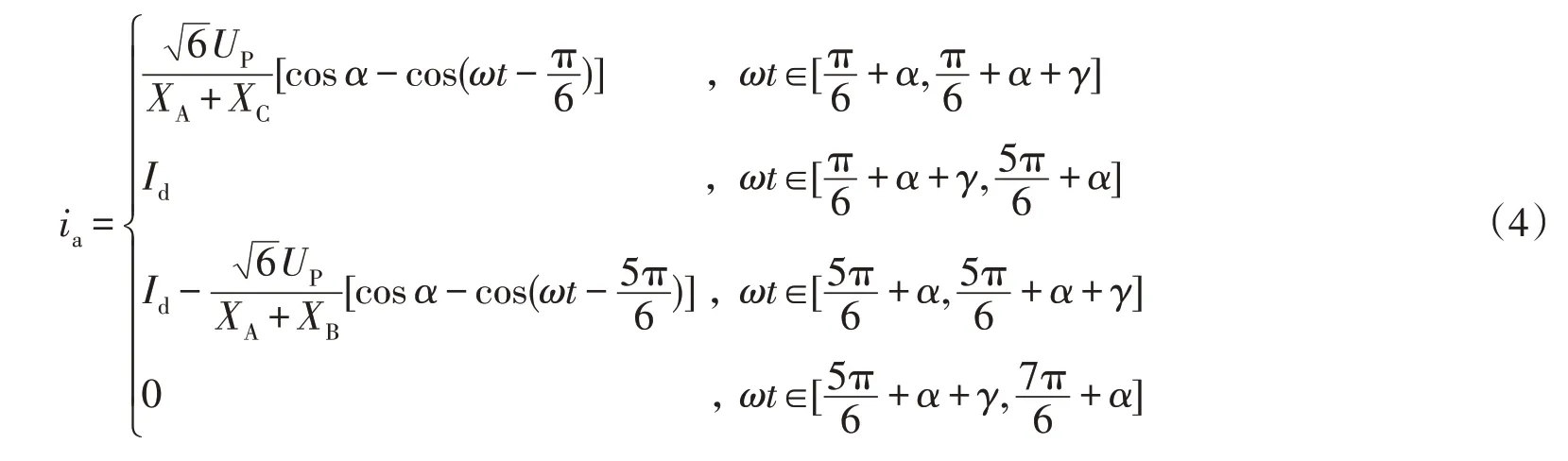
式中：XA、XB、XC为换流变压器三相电抗；α为晶闸管触发角；γ为换相重叠角。

下面以平衡运行、换流变压器三相阻抗不相等、晶闸管触发角存在偏差为例计算12 脉动换流器交流侧的谐波，分析不对称因素对非特征次谐波的影响，计算参数见表3。换流变压器相间阻抗不平衡取7.5%，触发角偏差取2.3°，直流侧电流为5 kA，计算结果见表4。

表3 换流器谐波计算参数Table 3 Calculation parameters of inverter harmonics

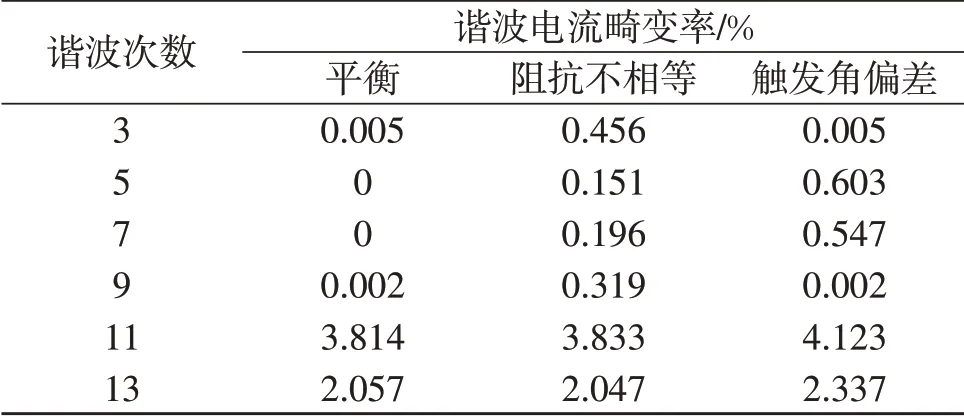
表4 各种工况下谐波含量Table 4 Harmonic content under different conditions

根据平衡运行、换流变压器三相阻抗不相等、晶闸管触发角偏差3 种工况下12 脉动换流器交流侧谐波计算结果可以看出在平衡的运行条件下，12脉动换流器交流侧只有11、13 次特征次谐波，而当出现换流变压器阻抗不相等、晶闸管触发角偏差时，非特征次谐波增加明显。

2 级联H桥APF

级联H 桥型变流器的拓扑结构最早在1996年由田纳西大学提出[21]，当时只用在了无功补偿的领域，而文献[22]提出了一种载波移相的正弦脉宽调制技术（CPS-SPWM）用于级联H 桥型变流器的控制，可以实现较好的滤波效果。本文针对换流站交流侧非特征次谐波无法有效滤除的问题，提出了一种基于级联H 桥的有源滤波器，其结构示意图见图4。

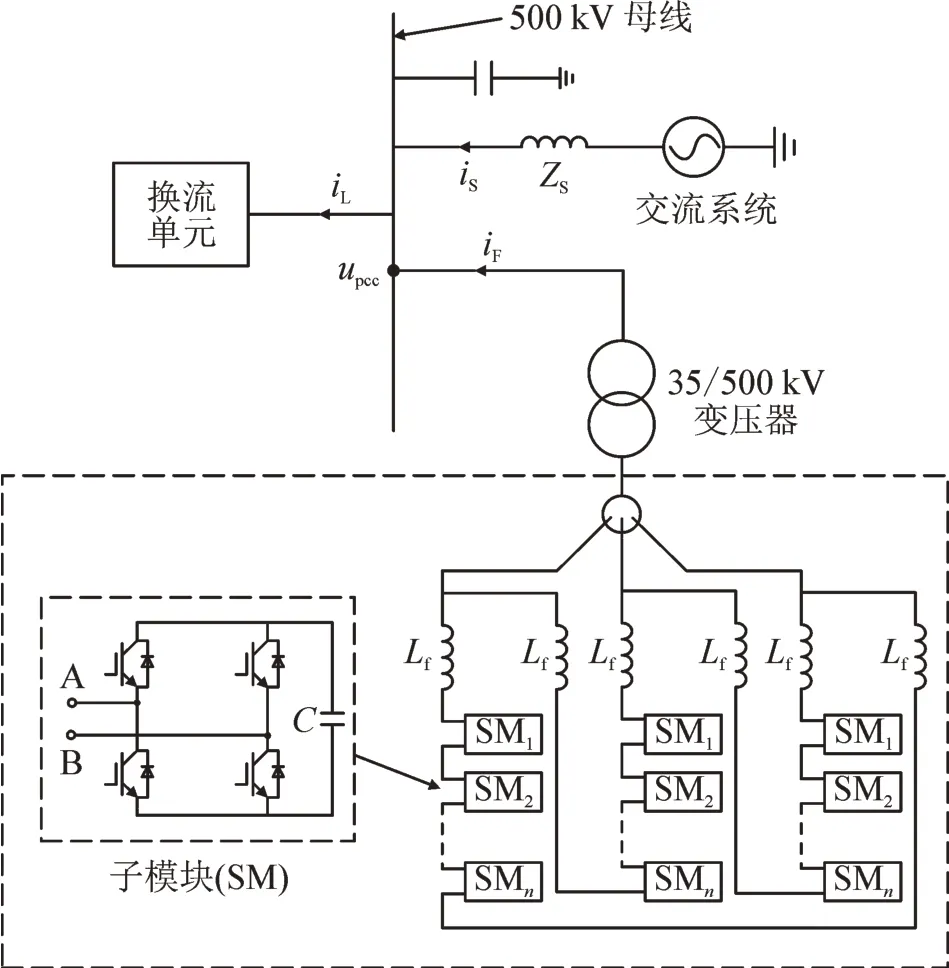
图4 级联H桥APF拓扑Fig.4 Topology of cascaded H-bridge APF

图中，级联H 桥APF 通过一台35/500 kV 的升压变压器与500 kV 高压母线相连，降低了级联H桥APF 所承受的电压，减少了级联的子模块个数。在级联H 桥APF 的连接方案方面对星形连接和三角形连接进行了对比[23-25]：1）两种连接方案都可以实现无功补偿和谐波电流补偿；2）星形连接无法补偿负序电流分量，否则会造成中性点电位偏移，造成设备过压；3）三角连接方案比星形连接方案实现的补偿容量更大；4）三角连接每相承担的都是固定的线电压，在系统电压不平衡时可靠性更高；5）星形连接每相承担的为相电压，需要级联侧子模块个数为三角连接的；在综合考虑经济性、运行可靠性、技术先进性的情况下，本文选择了三角形的连接方案。

在级联H 桥APF 的控制方面，本文采用PI 控制，级联H 桥APF 的简化分析图见图5。

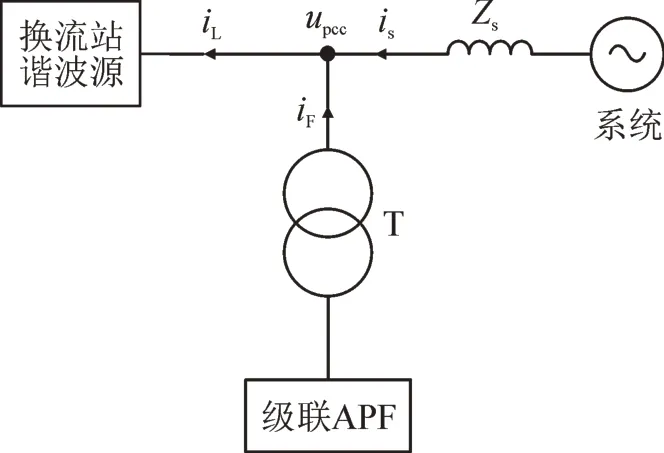
图5 级联H桥APF简化分析图Fig.5 Simplified analysis diagram of cascaded APF

图中，iL为流向换流器的电流，iF为级联H 桥APF 所在支路高压侧的电流，通过控制级联H 桥APF 的输出电压，使得其所在支路产生一个与iL中检测得到的谐波电流ih相等的电流iF并注入到系统中，从而让负载中的谐波电流可以被抑制；在级联APF 控制方面，谐波电流检测方法采用了Ip-Iq法，见图6，级联APF 的控制框图见图7。

图6 谐波电流检测Fig.6 Detection of harmonic current

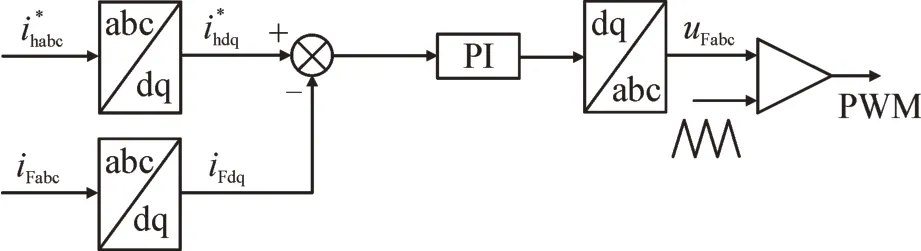
图7 级联APF控制框图Fig.7 Control block diagram of cascaded APF

图6 中，C32变换矩阵如公式（5）所示，C变换矩阵如公式（6）所示。

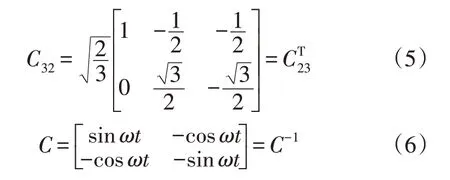
式中：ωt为锁相环输出相位；ih为检测得到的换流站谐波电流。图7 中，abc-dq 为派克变换；uFabc为级联APF 输出电压控制信号。

3 仿真分析

本文在PSCAD/EMTDC 中搭建了±800 kV 特高压直流输电和级联H 桥APF 的仿真模型，通过比较平衡运行时、不平衡运行时传统无源滤波器与所提级联H 桥APF 的滤波效果，验证了有源滤波器在抑制非特征次谐波方面有着更好的效果。

部分±800 kV 特高压直流输电和级联H 桥APF 的参数见表5，直流侧电压电流见图8-9。

表5 部分直流输电和级联APF参数Table 5 Parameters of partial DC transmission and cascaded APF

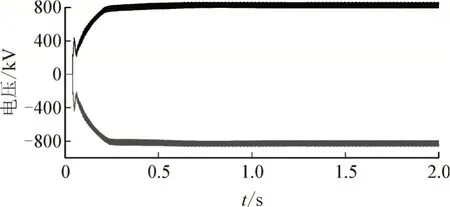
图8 直流侧电压Fig.8 Voltage at DC side

3.1 平衡运行时

平衡运行时，滤波之前以及经过滤波之后换流站三相电流波形以及A 相电流的谐波含量和级联APF 的输出电流仿真结果见图10-13。

在平衡运行时换流站未经滤波的三相电流以及A 相电流谐波含量如图9、图10 所示，其中A 相电流中主要包含11、13 次特征次谐波，出现3、5 及其附近次数谐波是因为无功补偿电容器与系统阻抗发生了谐振，前15 次的THD 为7.2%。

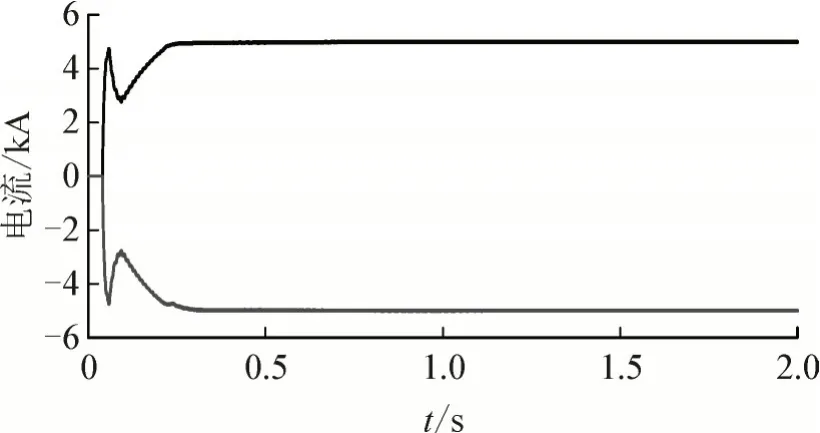
图9 直流侧电流Fig.9 Current at DC side

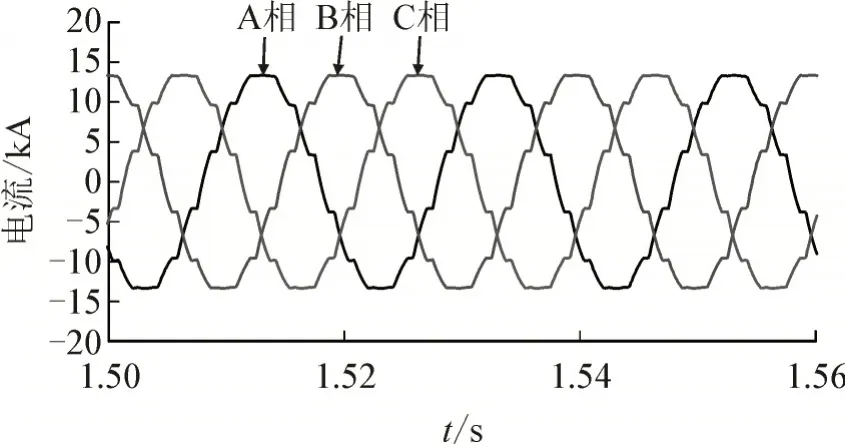
图10 平衡运行换流站三相电流Fig.10 Three-phase current of the converter station under balance working condition

经过无源滤波器和级联APF 滤波后的三相电流以及A 相电流谐波含量的对比如图11、图12 所示，在非特征次谐波含量方面：投入无源滤波器时A相仍含有63 A 的3 次谐波电流以及6.36 A 的5 次谐波电流；而投入级联APF 时A 相的3 次谐波降到了32 A，5 次谐波降到了1.4 A。在特征次谐波含量方面：投入无源滤波器时，仍含有19.9 A 的11 次谐波以及16.2 A 的13 次谐波；而投入级联APF 时，11次谐波降到了8.8A，13 次谐波降到了4.5 A。投入无源滤波器时前15 次的THD 为1.041%，而投入级联APF 时THD 则降到了0.7%。

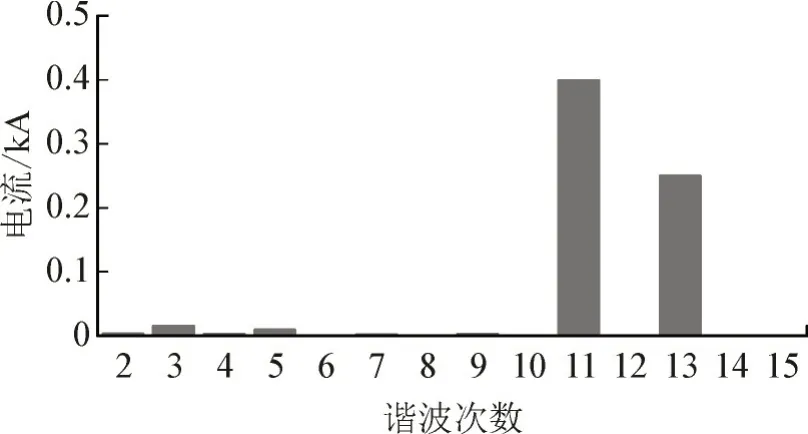
图11 平衡运行换流站A相电流谐波含量Fig.11 Harmonic content of current of phase A of converter station under balance working condition

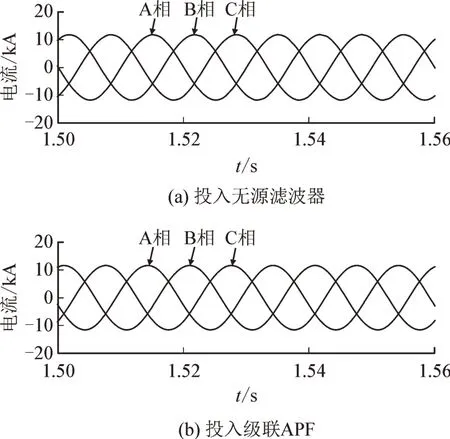
图12 平衡运行换流站滤波后三相电流Fig.12 Three phase current of balance operation converter station after filtering

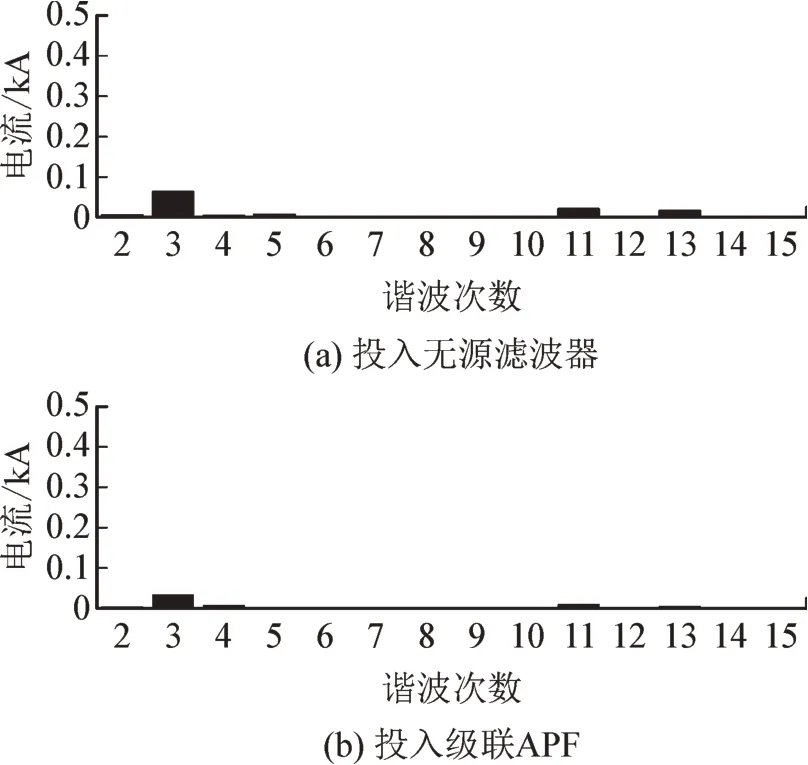
图13 平衡运行换流站滤波后A相电流谐波含量Fig.13 Harmonic content of current of phase A of balanced operation converter station after filtering

3.2 不平衡运行时

在不平衡运行时换流站未经滤波的三相电流以及A 相电流谐波含量见图14、图15，从图15 中可以发现在不平衡运行时，不仅含有大量的特征次谐波，非特征次谐波的含量增加的也较为明显，前15 次的THD 为9.96%。

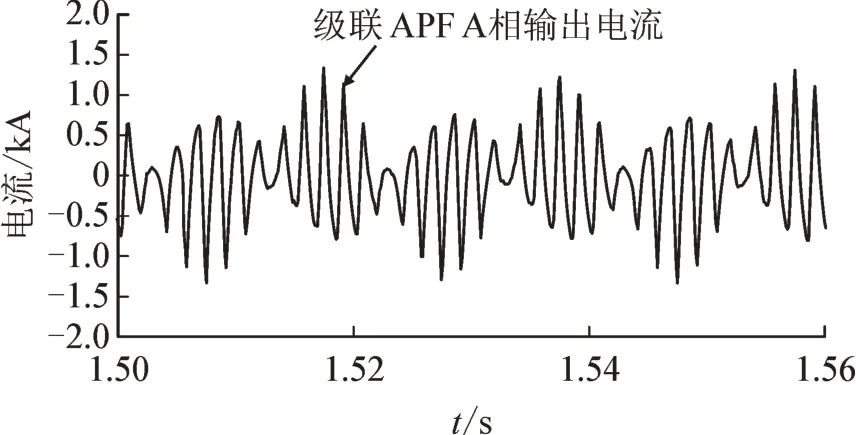
图14 平衡运行级联APF A相输出电流Fig.14 Output current of phase A of cascade APF under balanced operation

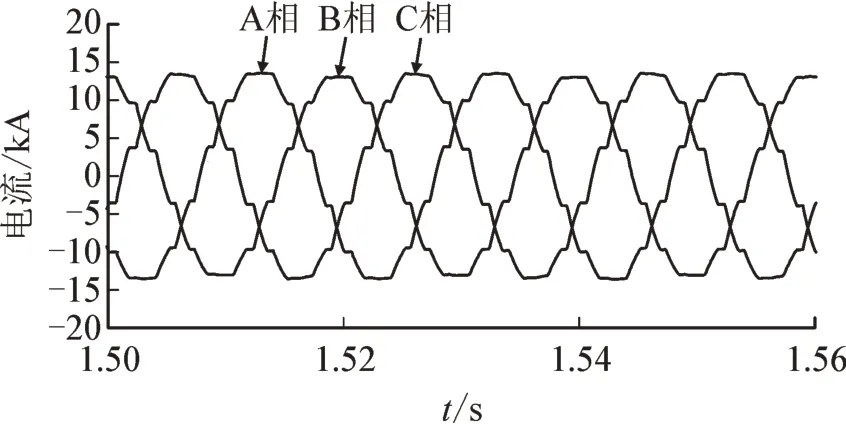
图15 不平衡运行换流站三相电流Fig.15 Three-phase current of the converter station under unbalance operation

经过无源滤波器和级联APF 滤波后的三相电流以及A 相电流谐波含量的对比见图16-19，在非特征次谐波含量方面：投入无源滤波器时A 相含有28 A 的2 次谐波电流、198 A 的3 次谐波电流、26 A的5 次谐波电流，其中2 次、3 次谐波电流比滤波之前的还要大，是因为无源滤波器与系统阻抗发生了谐振。

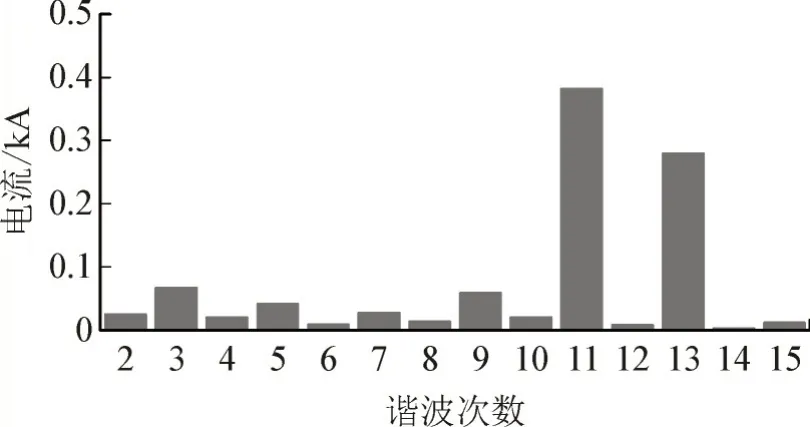
图16 不平衡运行换流站A相电流谐波含量Fig.16 Harmonic content of phase A of converter station under unbalance operation

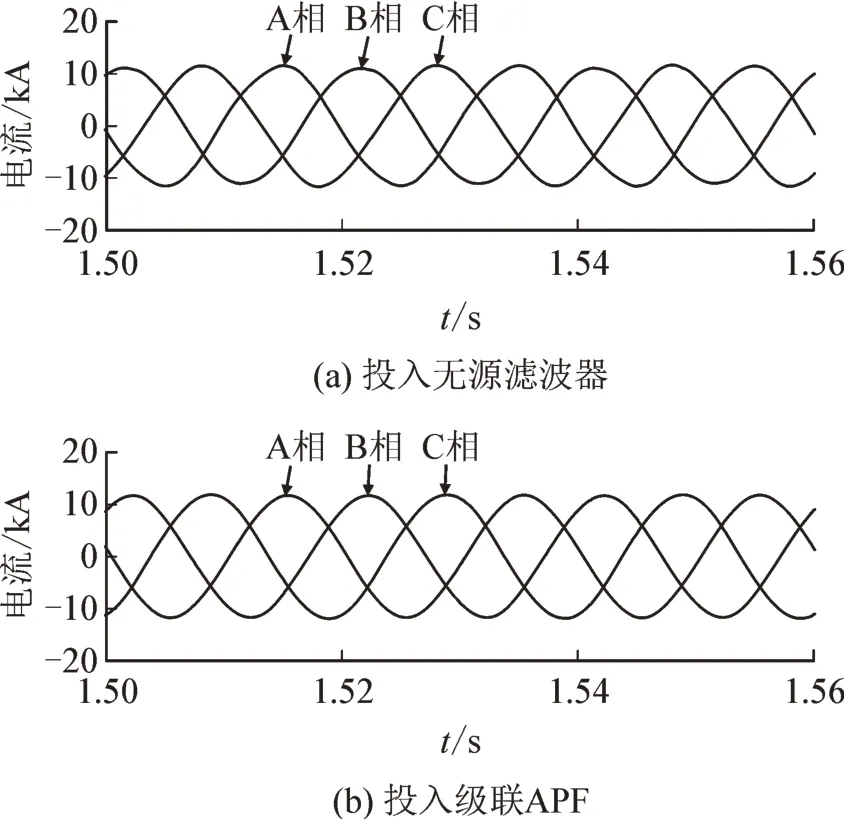
图17 不平衡运行换流站滤波后三相电流Fig.17 Three phase current of converter station under unbalance operation after filtering

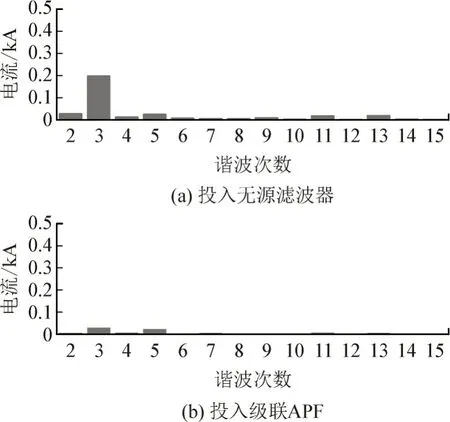
图18 不平衡运行换流站滤波后A相电流谐波含量Fig.18 Harmonic content of current of phase A in unbalanced operation converter station after filtering

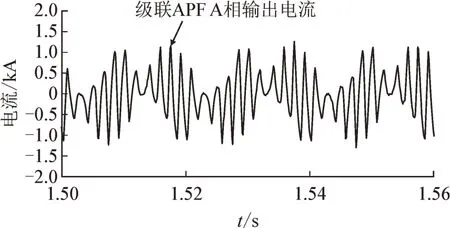
图19 不平衡运行级联APF A相输出电流Fig.19 Phase A output current of cascade APF under unbalanced working condition

而投入级联APF 时A 相的2 次谐波降到了4 A，3 次谐波降到了29 A，5 次谐波降到了22 A。在特征次谐波含量方面：投入无源滤波器时，仍含有18 A 的11 次谐波以及19 A 的13 次谐波；而投入级联APF 时，11 次谐波降到了6 A，13 次谐波降到了3 A。投入无源滤波器时前15 次的THD 为4.21%，而投入级联APF 时THD 则降到了1.02%。

4 结语

通过对换流站非特征次谐波的分析以及传统无源滤波器与所提级联APF 在特征次谐波和非特征次谐波滤波效果方面的对比，可以得到以下结论：

1）换流变压器三相阻抗不相等以及晶闸管触发角偏差等不平衡因素会导致换流站交流侧出现非特征次谐波。

2）级联APF 是主动滤波，可以有效地抑制换流站的特征次谐波与非特征次谐波，并且还可以避免与系统阻抗发生谐振导致谐波放大，比传统的无源滤波器有着更好的滤波效果。