对理论力学课程改革的期盼

胡海岩

(北京理工大学宇航学院，北京 100081)

在我国工程教育中，理论力学课程是一门历史悠久、体系严谨、具有基础性作用的重要课程。在我国科技和教育走向自立自强的新时代，如何推进该课程的教学改革面临若干值得探讨的问题。

笔者主要从事飞行器结构动力学与控制研究，并为飞行器设计专业的高年级本科生授课。因此，本文试图从理论力学课程的需求方视角，按照激发学生自主学习的教育理念，并根据培养工程科学家、研究工程师的思考和实践[1-2]，对理论力学课程的教学改革提出若干建议。

1 面向工程需求

在我国高校中，为工科本科生开设的理论力学课程有多种类别。既有不同学时要求的差异，也有面向机械工程类、能源动力类、土木工程类等区别。但从内容体系看，大多都按照静力学、运动学和动力学的顺序，而且例题和习题也很相似，与工程需求的联系并不密切，尚未体现对工业产品设计师、工程师的培养需求。

自20世纪以来，工业产品的力学设计经历了以下几个发展阶段。第一个阶段采用静态设计，包括机械和结构的静强度设计、静刚度设计等。第二个阶段采用静态设计+动态校核，后者包括机械和结构的固有振动校核、动响应的校核等。第三个阶段采用动态设计，包括机械和结构的振动设计、冲击设计、拓扑优化设计等。近年来，基于模型的系统工程（model based systems engineering，MBSE）、人工智能等新技术快速发展，使工业产品的力学设计水平进一步提升。

目前，在理论力学课程教学中，无论是现有教材，还是授课教师，都比较重视处理动力学正问题，即已知系统和驱动力来求系统运动。有些理论力学教材还指出，已知运动求力比较简单，而已知力求运动比较复杂，故主要关注后者。这样的教学理念和教学实践，可一定程度上满足工业产品的静态设计+动态校核需求。即基于材料力学、结构力学、弹性力学和有限元方法等进行静态设计，而理论力学只为动态校核提供求解动力学正问题的基本训练。

若从工业产品的动态设计需求看，学生今后需要解决的实际问题大多是动力学反问题，如已知驱动力和所需运动来设计系统，或已知系统和所需运动来设计驱动力。由于工业产品的力学模型大多无法简化为单个质点，求解其动力学反问题往往比求解其动力学正问题要困难，通常涉及欠定问题，没有唯一解。因此，现行的理论力学课程教学理念和教学实践，并未引导学生建立处理动力学反问题的基本概念，不利于学生未来从事工业产品的动态设计。

因此，在理论力学教学中，建议教师不仅强调理论力学的重要性，而且考虑理论力学课程如何为学生日后从事工业产品设计提供基础，帮助学生建立动态设计的基本概念和学术基础。

2 适应时代发展

根据陈立群教授的研究[3]，20世纪50～60年代，我国学者翻译了一批理论力学的俄语教材，对我国的工科理论力学教材建设产生了较大影响，形成目前大多数教材所采用的内容体系，即静力学+运动学+动力学。相比之下，我国的理科理论力学（或经典力学）教材受此影响较小。

改革开放以来，我国学者在编著工科理论力学教材时，从欧美大学的工科理论力学教材中吸收了若干精华，但教材体系和内容变化并不大。学生们普遍认为，现行的理论力学教材大同小异。根据笔者的考察，20世纪80年以来，欧美国家的理科经典力学教材比工科理论力学教材变化要大，体现了时代发展。在我国的工科理论力学教材建设中，似乎对欧美国家的理科经典力学教材尚未予以充分关注。

现以德国学者申科（Florian Scheck）教授所著的《力学：从牛顿力学到确定性混沌》为例，讨论上述问题。该书现已出版德语第8版和英语第6版[4]，是欧洲大学物理专业常用的经典力学教材。与20世纪80年代前的理科经典力学教材相比，该书约65%的内容来自传统体系，包括质点动力学、质点系动力学、刚体动力学、分析力学、狭义相对论等，但融入了许多新内容。例如：在经典内容中融入几何力学思想，介绍了相空间的辛结构，哈密顿（Hamilton）系统摄动，哈密顿力学框架下的刚体力学等，还介绍对称性与诺特（Noether）定理等。该书以约15%的篇幅介绍几何力学，先介绍微分流形、外代数和外微分等数学工具，然后基于近代几何讨论经典力学；包括拉格朗日（Lagrange）力学在切丛上的性质，哈密顿力学在余切丛上的性质，力学中的黎曼（Riemann）流形等，体现了近代几何和经典力学的深度融合。该书还以约20%的篇幅介绍力学系统的稳定性和混沌，充分体现非线性科学对物理学发展的影响。笔者认为，该书前65%的内容适用于本科生学习，后35%的内容适用于研究生学习。该书的特点是，在前者中穿插介绍了后者的若干研究结论，可激发本科生的学术兴趣，并帮助读者实现认识过程的螺旋上升。

因此，在谋划工科理论力学课程的改革时，建议重视理科经典力学教材的上述变化。理科教育和工科教育有显著差异，其优势在于基础性。理论力学作为基础性的力学课程，自然要适应时代发展对人才培养的强基要求，有利于学生未来的自主学习。对于综合性大学所设立的理论与应用力学专业，其理论力学课程的改革更需要体现有助于学生掌握坚实的理论基础。

3 提升学术品位

受学时限制，在工科理论力学课程中难以大幅度增加分析力学的内容，也难以引进几何力学的内容。然而，为了提升学生的学术品位，教师可引导学生对若干重要的概念、方法和公式作深入地思考和探索，提升理论素养，为自主学习几何力学奠定基础。

例如，刚体上任意点B相对于基点A的速度向量其中，是刚体转动的角速度向量，是由基点A到点B的向量。如果采用不带箭头的符号表示向量的坐标列阵，则可表示为

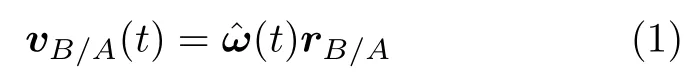
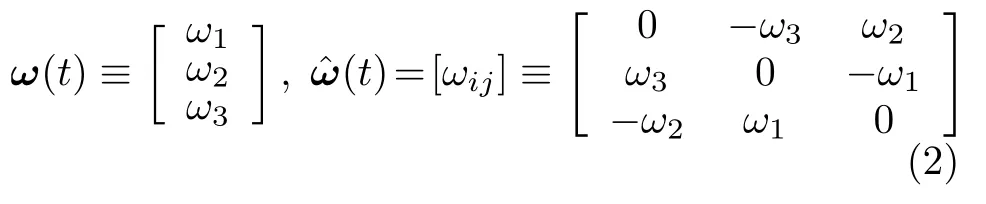
从形式上看，从式(1)到式(2)只是表达方式的变化。但从内涵看，反对称矩阵是二阶反对称张量的坐标矩阵，可说明角速度向量ω(t)是赝向量（轴向量），而不是真向量（线向量）。

对式(3)进一步讨论，可得到李群SO(3) 与李代数so(3) 间的指数映射，这是几何力学的重要内容。

再进一步，可将刚体转动描述延伸到微分几何。在空间曲面上的任意点p，建立由正交基向量列阵构成的局部正交标架{p;e1,e2,e3}。当点p在曲面上移动时，该正交标架作刚体运动。根据线性代数，基向量列阵ei的微分 dei可由基向量列阵来线性表示，即

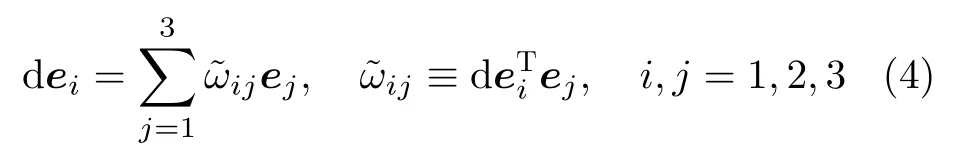
实践证明，在教师引导下，本科生如果能深刻理解刚体转动的几何意义，就可以自主学习李群和李代数、微分几何等知识，进而用现代数学工具来处理复杂的动力学问题。

4 拓展学术视野

翻阅现行的理论力学教材，可发现一个共同点，即多数例题和习题的讨论对象是滑轮、曲柄连杆机构等，而不是现代科技和工程中的问题。理论力学是工程教育中公认有难度的课程，需要通过大量的解题训练来巩固学习，但这些过于传统的例题和习题难以激发学生的兴趣。可以设想，若学生与正在工程技术一线的毕业生交流，无疑会对这些例题和习题失望，由此导致对整个理论力学课程的失望。

因此，建议在理论力学的教学改革中，对例题和习题进行更新和升级，融入现代科技和工程要素。理论力学课程虚拟教研室可作为一个工作平台，凝聚来自多所高校的教师通力合作，搜集来自高端装备制造、先进能源与动力、基础设施建设等方面的工程案例。此外，在贾书惠[5]教授所著《漫话动力学》和刘延柱[6]教授所著《趣味刚体动力学》中，也有许多值得采纳的优秀案例。

在理论力学课程的例题和习题中，还可适度融入与生物力学相关的内容。例如，体操、瑜伽中的静平衡问题；又如，跳高、跳水、冰雪运动中的运动学和动力学问题；再如，对人体腹式呼吸与逆腹式呼吸的受力分析等。融入这些内容，可望使学生拓展学术视野，在更广阔的学术领域中自主思考未来发展。

5 结束语

在理论力学课程的教学改革中，建议以激发学生自主学习为改革思路，关注如何面向工程需求、适应时代发展、提升学术品位、拓展学术视野等问题。这些问题彼此相互关联，故建议基于系统科学对教学改革进行整体谋划、优化设计和逐步实践。